双自由度离心振动系统的动力耦合分析

刘占芳，郭小炜

（重庆大学资源及环境科学学院，重庆 400030）

引 言

旋转结构的动特性和动力响应分析是进行旋转机械和旋转结构可靠性设计和安全性评价的理论基础。进行风力发电机风轮、直升机螺旋桨、离心机叶轮及其叶片设计时，了解旋转结构的特征频率变化既是材料选取和结构优化的依据，也为避免结构共振实施控制策略提供关键参数。旋转结构的动力分析涉及结构的变形以及应力状态等，为结构变形控制和强度校核、确定动态测试方案提供基础的分析数据。由于旋转结构运行在离心环境下，结构自身的弹性变形与旋转运动耦合在一起，造成离心环境严重影响结构的动特性和动力学响应。譬如风力机风轮的坎贝尔图是关于风轮的各阶频率与风轮转速的关系［1］，可为风轮共振分析和风电机组控制提供设计和分析参数。因为旋转结构动力学在实际工程中的巨大应用价值，几十年来引起了学术界和工程界的持久兴趣。直到最近，大量的文献依然关注旋转的杆梁结构、旋转环、旋转盘和板、旋转壳的振动特性和响应［2～23］，其中旋转结构的科氏力效应，动力刚化问题，旋转角速度对结构特征频率的影响，复值的特征矢量和复模态处理等是研究重点，特别是旋转和变形的耦合机制还不完全清楚，解决这些问题有赖于揭示刚体旋转与弹性变形的耦合机理，建立精确可靠的动力学分析模型，发展合适的算法以及实验或工程验证。

旋转结构较之非旋转结构的复杂性在于结构进一步承受由于运动耦合带来的附加惯性力，这种附加惯性力影响结构动力学，同时结构变形影响结构的刚性旋转运动。为揭示运动变形耦合以及对结构动力学造成的影响，本文引入双自由度的质量弹簧振动系统作已知的刚体旋转，系统可考虑刚体旋转形成的初始离心力、质量点振动造成的离心力改变以及科氏力等。这种简化模型既不失去结构变形与刚体旋转耦合的典型特性，又可通过考察简单物理模型来探讨动力学规律，为复杂结构的动力学分析提供清晰的参考。

1 双自由度离心振动系统的动力学模型

考虑刚体绕定轴作匀速圆周运动，转动的角速度为ω，刚体上任意一点r的线速度v为

二阶反对称张量Ω可表示旋转轴和绕轴旋转角速度，即有［24］

式中e为笛卡尔坐标系下的置换张量，角速度ω为反对称张量Ω的反偶矢量或轴矢量。二阶反对称张量Ω对任意矢量u的映射为

二阶反对称张量只关联着转动角速度，正交张量能描述刚体作定轴有限转动的旋转角速度和旋转角。现令单位矢量n代表旋转轴方向，θ为旋转角，引进反对称张量A＝－e·n，对正交张量R有［25］

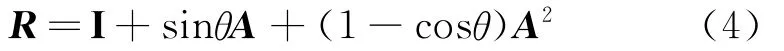
上式为Euler－Rodrigues旋转公式。对匀速转动，正交张量R可进一步改写为

ω为角速度矢量ω的模。

现在关注一个质量点m与4个相同弹簧组成的双自由度振动系统作平面刚体旋转运动（忽略振动造成的离心振动系统转动惯量的变化），振动系统固定在刚体上以垂直于旋转平面的恒角速度ω作逆时针旋转。建立固定和转动两个坐标系，见图1，质量点的初始位置r0为转动坐标系的原点，两个坐标基分别沿转动的径向和切向，质量点在转动坐标系的振动位移为r，则质量点在转动坐标系的位置为r0＋r。由于正交张量描述了刚体有限转动，则任意时刻质量点在固定坐标系的位置为

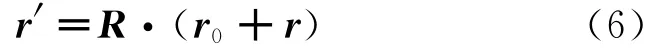
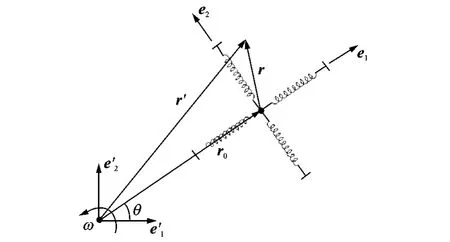
图1 双自由度振动系统作定轴平面转动Fig．1 The vibrating system with two degrees of freedom rotates around with a fixed axis

这里正交张量R代表转动坐标系与固定坐标系构成的两点张量。对式（6）取时间导数，利用式（3）和（5）得质量点在固定坐标系的绝对速度为

再对式（7）取时间导数并再次应用式（3）和（5），得固定坐标系下质量点的绝对加速度为

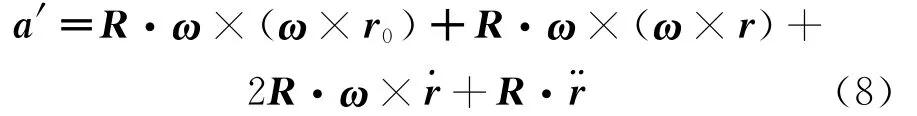
式（7）和（8）中˙r和¨r表示质量点在转动坐标系的振动速度和加速度。利用正交张量的转置张量RT立即得到在转动坐标系下质量点的绝对加速度

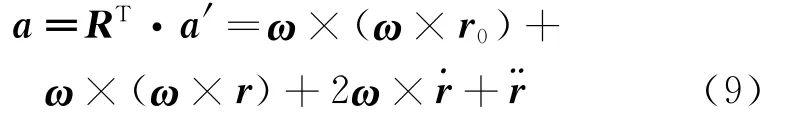
式中ω×（ω×r0）为振动系统的初始向心加速度、ω×（ω×r）是由于质量点振动导致的向心加速度增量、2ω×˙r为科氏（Coriolis）加速度。由此可知，如果质量点在垂直于旋转平面的方向上运动，不产生科氏加速度和向心加速度的增量。

应用达朗贝尔原理，忽略质量点重力作用，可建立质量点m在转动坐标系的动力学方程

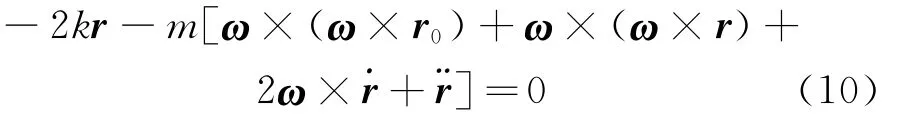
k为弹簧的弹性系数。由式（10）可知，质量点m受到弹簧回复力、相对惯性力、初始离心力、离心力增量和科氏力的共同作用，注意到质点动力学方程（10）与旋转角θ无关。由于质量弹簧系统的刚体转动和振动都在旋转平面上（图1），在转动坐标系中有

u和v表示在转动坐标系质量点的两个位移分量，进一步令r0的模为r0。利用式（11）以及矢量的二重叉积公式，改写式（10）得到沿转动坐标系两个坐标轴e1和e2的动力学方程

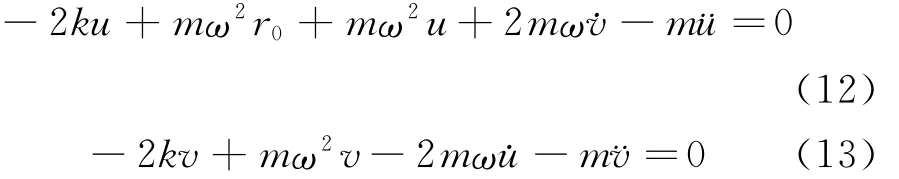
把式（12）和（13）联立成为矩阵形式

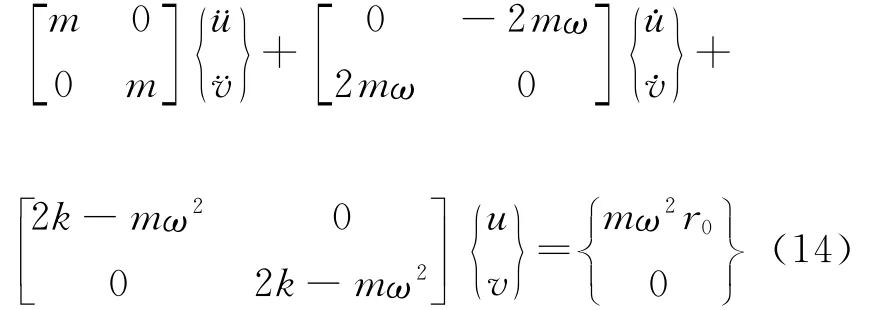
改写式（14）得离心振动系统动力学方程的一般形式

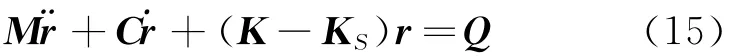
式（15）中质量矩阵M，科氏矩阵C，振动刚度矩阵K，离心矩阵KS分别为：

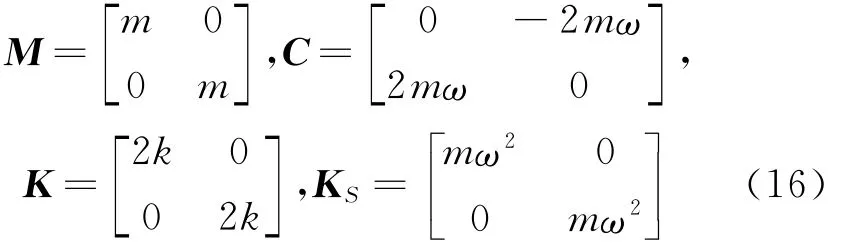
科氏矩阵C为反对称矩阵，尽管在动力学方程出现一阶项但不造成系统的阻尼衰减。式（15）也是线弹性情况下旋转结构动力学方程的典型形式。观察式（14）可知在旋转平面内，由于刚体旋转与弹性振动的运动耦合产生科氏力，导致u和v两个方向的运动也是耦合的，而运动耦合也反之影响科氏力，这正是离心振动系统复杂性的本质。此外，离心振动系统刚度阵K－KS的系数应为正，表明为保持系统稳定应存在最大刚体转速，下面将进一步说明。

2 双自由度离心振动系统的动频和动模态

为研究离心振动系统的动力学性质，将动力学方程（15）改写成下述形式

记zT＝｛u˙uv˙v｝T，则式（17）在形式上成为一阶非齐次线性微分方程组

式（18）中的T和g取与式（17）右端对应的方阵和列阵。方程组（18）的齐次方程解的形式为z＝Cφeλt，对应的特征方程为｜T－λI｜＝0，容易得到系统的特征值为

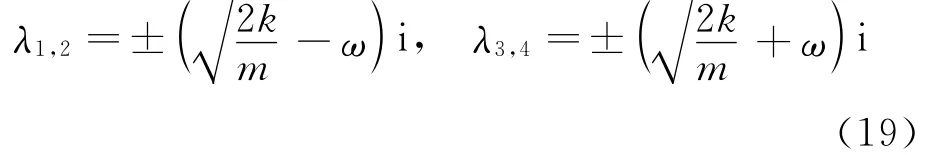
ω1＝分别表示振动系统两阶模态的圆频率，而f1和f2分别为随转速变化的两阶动频。作为例子，令m＝0．1kg，k＝10 N／m。系统两阶特征频率随转速变化的曲线见图2。当转速为零时刚体旋转对振动的影响消失，系统的两阶动频退化为系统的固有频率（基频）。随刚体转速增加系统的第一阶动频f1线性减小而第二阶动频f2线性增加，当转速达到固有频率时，第一阶动频趋于零，表示刚体转动造成了振动系统失稳，所以，刚体的最大转速等于质点振动的固有频率。

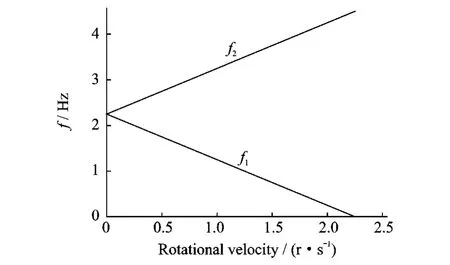
图2 离心振动系统的两阶动频与旋转运动（转速）的关系Fig．2 Two order dynamic frequencies of the centrifugal vibrating system vary with rotational velocity

对式（18）的齐次形式以及式（19）的特征值，可以确定特征值对应的广义特征矢量。令λ1＝－ω1i，λ2＝ω1i，λ3＝－ω2i，λ4＝ω2i，所对应的广义特征矢量分别为

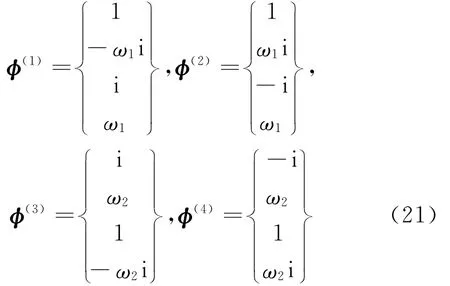
特征值λ1，λ2，λ3，λ4所对应的复值解分别为

利用线性微分方程组解的可叠加性，对每组复值解作简单的代数运算可得到每个特征值所对应的线性独立的实值解，即为两阶模态，它们分别为

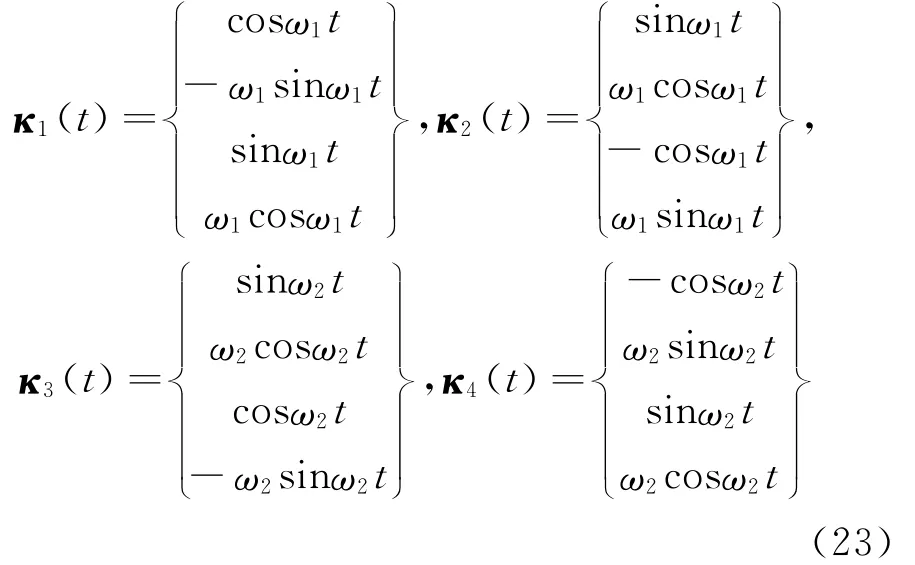
两阶模态都是刚体转速ω的函数。κ1和κ2表示系统的第1阶动模态，κ3和κ4表示系统的第2阶动模态。注意到这些实值解列阵中的第1行和第3行分别为质量点的两个模态位移分量，显然，两个模态位移分量的平方和均为1，表明系统的两阶动模态都是半径为1的极化圆周运动，模态圆周运动以及模态位移的初始位置（相位）见图3。系统第1阶动模态的转动方向为逆时针，圆周运动的角速度即为系统第1阶圆频率ω1。第2阶动模态的转动方向为顺时针，圆周运动的角速度即为系统第2阶圆频率ω2。第1阶动模态的转动速度随系统转速ω的增加变得越来越慢，直至趋于第1阶动频的最小值，而第2阶动模态的转动速度随转速ω的增加会变得越来越快。

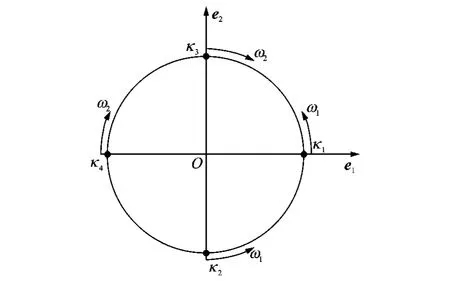
图3 离心振动系统两阶动模态的极化圆周运动及其相位Fig．3 The polarized circular motion with the two order dynamic modal and the phase of the centrifugal vibrating system

3 双自由度离心振动系统的质点运动轨迹

根据式（23）可写出方程组（18）的齐次形式的基解矩阵为

由于Z（0）≠I，可以选取基解矩阵为Z′（t）＝Z（t）Z－1（0），则非齐次微分方程组（18）的通解形式为［26，27］

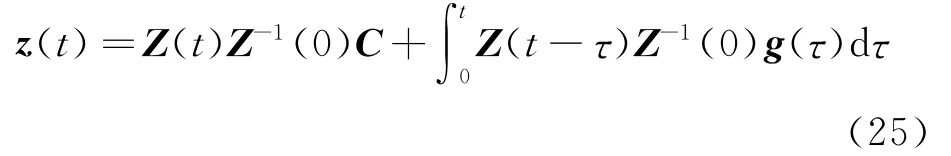
将式（24）带入到式（25）可得

令振动系统的初始条件为t＝0时，u（0）＝u0，˙u（0）＝˙u0；v（0）＝v0，˙v（0）＝˙v0。将初始条件代入式（26）和（27）中可得振动系统响应解的系数

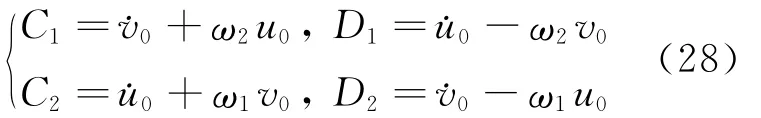
质点的动力学响应即为质点的平面运动轨迹，由式（26），（27）以及（28）可知，质点的运动轨迹取决于振动初始条件、振动刚度、刚体转速、质点初始位置r0。由于质点振动的同时作平面刚体转动，所以质点初始位置可视为离心振动系统的初始偏心位置。

为考察质点的运动轨迹，进一步令振动的初始条件t＝0．0s时，u（0）＝0．1m，v（0）＝0．05m，˙u（0）＝˙v（0）＝0．0m／s，初始偏心位置r0＝0．4m。当刚体转速分别为ω＝0．25r／s和ω＝1．0r／s时，质点的位移时程曲线见图4和5。根据质点随时间变化可以得到质点在转动坐标系下的平面运动轨迹，图6为刚体转速ω＝0．25r／s和ω＝1．0r／s时的质点运动轨迹，对给定的初始条件和振动刚度，质点的运动轨迹和振幅强烈依赖于刚体转速。图7表示质点振幅与转速的关系曲线，在一定的振动刚度和振动初始条件下，存在一个临界转速（在本例中为1．0r／s），超过临界转速后，质点振动幅值会迅速增加，超越线性振动的范围。前面关于系统动频的分析提到过刚体的最大转速，但对质点动力响应的分析表明，为保持系统的线性振动，刚体的转动应该小于刚体临界转速。

观察式（26）和（27）右端可以发现，质点的运动实际上由非偏心运动和偏心运动两部分构成，非偏心运动取决于振动初始条件、刚体转速和振动刚度，而偏心运动依赖于初始偏心位置、刚体转速和振动刚度。

图4 刚体转速为0．25r／s时的位移时程曲线Fig．4 Mass displacement history atω＝0．25r／s

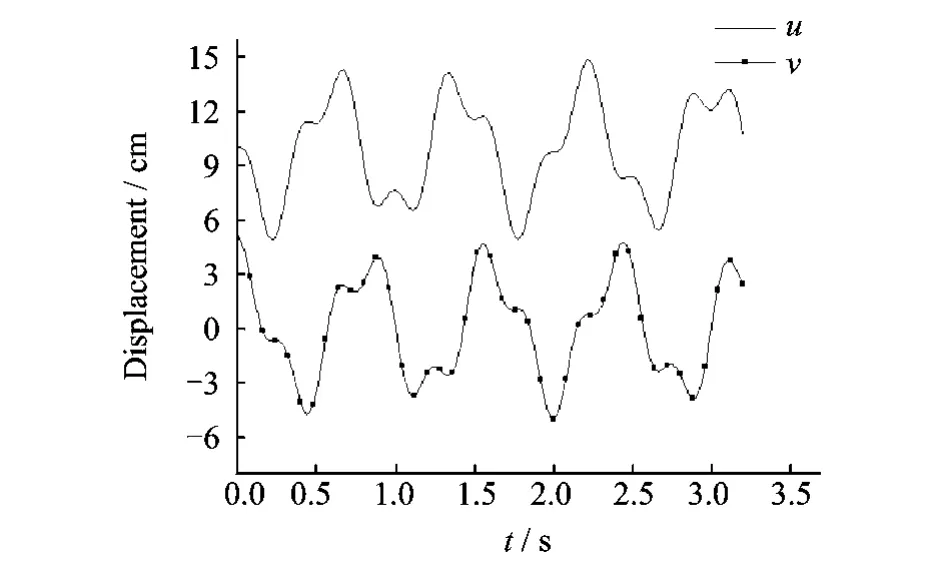
图5 刚体转速为1．0r／s时的位移时程曲线Fig．5 Mass displacement history atω＝1．0r／s

图6 转速为0．25r／s和1．0r／s时质点的运动轨迹Fig．6 Mass trajectories atω＝0．25r／s andω＝1．0r／s

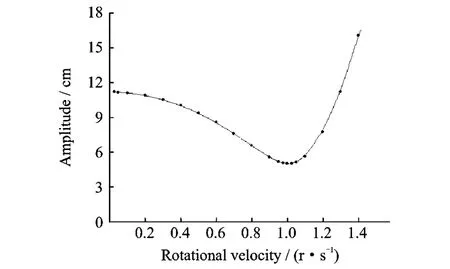
图7 质点振幅随刚体转速的变化Fig．7 Mass displacement amplitude vary with the rotational velocityω

图8和9分别为刚体转速为0．2 5r／s和1．0 r／s时分解的非偏心运动和偏心运动轨迹，注意到非偏心运动的幅值在不同刚体转速下是相同的，而偏心运动的幅值强烈依赖于刚体转速。当刚体转速为0．25r／s时，质点的运动轨迹主要是非偏心运动轨迹，偏心运动的影响很小。当刚体转速为1．0r／s时，偏心运动的影响显著影响质点总的运动轨迹。当初始偏心位置和振动刚度一定，偏心运动幅值随刚体转速增加而增大，考虑到非偏心运动和偏心运动的相位因素，这解释了图6和7的质点振幅随刚体转速先降后升的变化，特别是刚体转速超过某一临界值时，偏心运动逐渐主导了质点的运动轨迹。

图8 转速为0．25r／s时的非偏心运动和偏心运动轨迹Fig．8 Split non－eccentric and eccentric motional trajectories of the mass atω＝0．25r／s under rotating

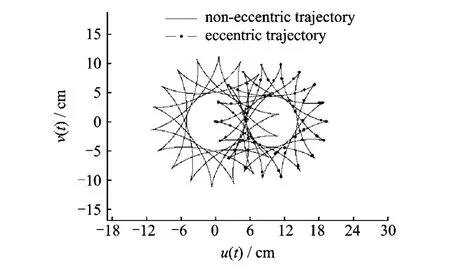
图9 转速为1．0r／s时的非偏心运动和偏心运动轨迹Fig．9 Split non－eccentric and eccentric motional trajectories of the mass atω＝1．0r／s under rotating

4 结 论

本文借助双自由度离心振动系统的简单模型，讨论了大范围刚体转动和双自由度振动的耦合动力学问题。在已知刚体转动中，质点受到弹簧回复力、相对惯性力、初始离心力、离心力增量和科氏力。随着刚体转速的增加，第1阶动频线性降低而第2阶动频线性增加，刚体的最大转速就是振动系统的固有频率。双自由度离心振动系统的两阶模态都是极化的圆周运动，圆周运动的角速度对应于系统的两阶圆频率。

离心振动系统的质点运动轨迹与振动初始条件、振动刚度、刚体转速和初始偏心距离有关。质点运动轨迹由非偏心运动和偏心运动两部分构成，非偏心运动取决于振动初始条件、振动刚度和刚体转速，偏心运动取决于初始偏心距离、振动刚度和刚体转速，当初始偏心距离和振动刚度一定，偏心运动的振动幅值随刚体转速增加而增加。在有初始偏心情况下，离心振动系统存在临界刚体转速，超过临界转速后质点振动幅值迅速升高。对于大范围刚体运动下的线弹性振动系统，为保持线弹性范围内的振动，应考虑临界的刚体转速。

［1］ Park J H，Park H Y，Jeong S Y，et al．Linear vibration analysis of rotating wind－turbine blade［J］．Current Applied Physics，2010，10（2）：332—334．

［2］ Shum W S，Zhang L．Dynamic motion of whirling rods with Coriolis effect［J］．Applied Mathematical Modelling，2010，34：1 203—1 216．

［3］ Huang C L，Lin W Y，Hsiao K M．Free vibration analysis of rotating Euler beams at high angular velocity［J］．Computers and Structures，2010，88（17－18）：991—1 001．

［4］ Turhan O，Bulut G．On nonlinear vibrations of a rotating beam［J］．J．Sound and Vibration，2009，322（1－2）：314—335．

［5］ WEBER H I．A note on the stability of a rod subjected to compression by centrifugal force［J］．J．Sound and Vibration，1976，46（1）：105—111．

［6］ Lin S C，Hsiao K M．Vibration analysis of a rotating Timoshenko beam［J］．J．Sound and Vibration，2001，240（2）：303—322．

［7］ Cai G P，Hong J Z，Yang S X．Dynamic analysis of a flexible hub－beam system with tip mass［J］．Mechanics Research Communications，2005，32（2）：173—190．

［8］ 蒋丽忠，洪嘉振．大范围运动对弹性梁振动频率及模态的影响［J］．振动与冲击，1999，18（1）：12—16．

Jiang Lizhong，Hong Jiazhen．The frequency and mode of elastic beams in large overall motions［J］．Journal of Vibration and Shock，1999，18（1）：12—16．

［9］ 刘锦阳，洪嘉振．大范围运动空间梁的耦合动力学模型［J］．上海交通大学学报，2003，37（4）：532—534．

Liu Jinyang，Hong Jiazhen．Coupling dynamic modeling of the spatial beam under going large overall motions［J］．Journal of Shanghai Jiao Tong University，2003，37（4）：532—534．

［10］刘锦阳，李彬，洪嘉振．作大范围空间运动柔性梁的刚－柔耦合动力学［J］．力学学报，2006，38（2）：276—282．

Liu Jinyang，Li Bin，Hong Jiazhen．Rigid－flexible coupling dynamics of a flexible beam with three－dimensional large overall motion［J］．Chinese Journal of Theoretical and Applied Mechanics，2006，38（2）：276—282．

［11］章定国，余纪邦．作大范围运动的柔性梁的动力学分析［J］．振动工程学报，2006，19（4）：475—480．

Zhang Dingguo，Yu Jibang．Dynamical analysis of a flexible cantilever beam with large overall motions［J］．Journal of Vibration Engineering，2006，19（4）：475—480．

［12］Lin J L，Soedel W．On general in－plane vibrations of rotating thick and thin rings［J］．J．Sound and Vibration，1988，122（3）：547—570．

［13］Kim W，Chung J．Free non－linear vibration of a rotating thin ring with the in－plane and out－of－plane motions［J］．J．Sound and Vibration 2002，258（1）：167—178．

［14］Eley R，Fox CHJ，McWilliam S．Coriolis coupling effects on the vibration of rotating rings［J］．J．Sound and Vibration，2000，238（3）：459—480．

［15］Chen J S．On the linearization of the equations of motion of a rotating disk［J］．Applied Mathematical Modelling，2011，35（1）：392—397．

［16］Baddour N，Zu J W．A revisit of spinning disk models．Part I：Derivation of equations of motion［J］．Applied Mathematical Modelling，2001，25（7）：541—559．

［17］Mignolet M P，Eick C D，Harish M V．Free vibration of flexible rotating disk［J］．J．Sound and Vibration，1996，196（5）：537—577．

［18］Hashemi S H，Farhadi S，Carra S．Free vibration analysis of rotating thick plates［J］．J．of Sound and Vibration，2009，323（1－2）：366—384．

［19］Maretic R．Transverse vibration and stability of an eccentric rotating circular plate［J］．J．of Sound and Vibration 2005，280（3－5）：467—478．

［20］刘锦阳，洪嘉振．作大范围运动矩形薄板的建模理论和有限元离散方法［J］．振动工程学报，2003，16（2）：175—179．

Liu Jinyang，Hong Jiazhen．Dynamic modeling theory and finite element method for a rectangular plate un－dergoing large overall motion［J］．Journal of Vibration Engineering，2003，16（2）：175—179．

［21］赵飞云，洪嘉振．作大范围运动矩形板的动力学建模理论研究［J］．计算力学学报，2008，25（6）：868—873．

Zhao Feiyun，Hong Jiazhen．Study on dynamic modeling of rectangular plates undergoing large overall motion［J］．Chinese Journal of Compu－tational Mechanics，2008，25（6）：868—873．

［22］Wang Y Q，Guo X H，Chang H H，et al．Nonlinear dynamic response of rotating circular cylindrical shells with precession of vibrating shape－Part I：Numerical solution［J］．Inter．J．Mechanical Sciences，2010，52（9）：1 217—1 224．

［23］Liew K M，Ng T Y，Zhao X，et al．Harmonic reproducing kernel particle method for free vibration analysis of rotating cylindrical shells［J］．Computer Methods in Applied Mechanics and Engineering，2002，191（37－38）：4 141—4 157．

［24］黄克智，薛明德，陆明万．张量分析［M］．北京：清华大学出版社，2003．

Huang Kezhi，Xue Mingde，Lu Mingwan．Tensor A－nalysis［M］．Beijing：Tsinghua University Press，2003．

［25］Palais B，Palais R．Euler’s fixed point theorem：the axis of a rotation［J］．J．Fixed Point Theory and Applications，2007，2：215—220．

［26］蔡燧林，盛骤．常微分方程组与稳定性理论［M］．北京：高等教育出版社，1988．

Cai Suilin，Cheng Zhou．Ordinary Differential Equations and Stability Theory［M］．Beijing：Higher Education Press，1988．

［27］马知恩，王绵森．工科数学分析基础（下册）［M］．北京：高等教育出版社，1999．

Ma Zhien，Wang Miansen．Engineering Mathematics Analysis （part II）［M］．Beijing：Higher Education Press，1999．