经典功率谱估计方法的研究

俱莹，何佳，胡稷鑫

（国家无线电监测中心陕西监测站，西安　710200）

经典功率谱估计方法的研究

俱莹，何佳，胡稷鑫

（国家无线电监测中心陕西监测站，西安710200）

本文主要针对随机信号处理中最重要的统计表征——功率谱密度，研究了经典功率谱估计的方法，包括自相关函数法和周期图法。通过仿真分析了几种方法的性能，研究了窗长度、窗函数及信噪比等对谱估计性能的影响，为工程应用中谱估计方法及参数的选择提供了依据。

功率谱密度；自相关函数法；周期图法；分辨率

1　引言

随机信号在各个时间点上的取值是不能先验确定的，但是可以用它的统计平均特性来表征［1］。一个无限持续期无限能量的平稳随机序列的傅里叶变换是不存在的，无法求得频谱，但它的功率有限，功率谱密度存在，因此，功率谱密度［2-4］是随机信号最重要的表征形式。

2　经典功率谱估计方法

根据维纳辛钦定理，自相关函数和功率谱密度是一对傅里叶变换，可以通过对自相关函数求傅里叶变换得到随机信号的功率谱，经典谱估计方法就是基于上述思想而提出的［5-7］。但是实际中样本序列总是有限长的，所以无法求得准确的自相关函数的值，只能通过一段样本的值来进行功率谱估计，目前常用的有两种方法：自相关函数法和周期图方法。

2.1自相关函数法

假设已知随机信号x（n）的N个观测样本，则其自相关序列可用下式估计

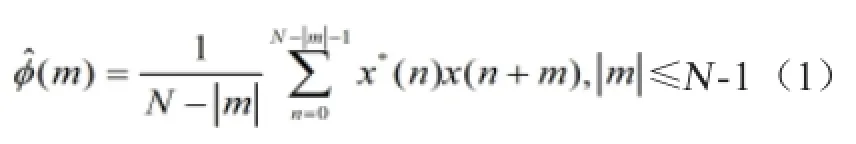
当仅用长度为2M-1的自相关序列时，得到功率谱估计

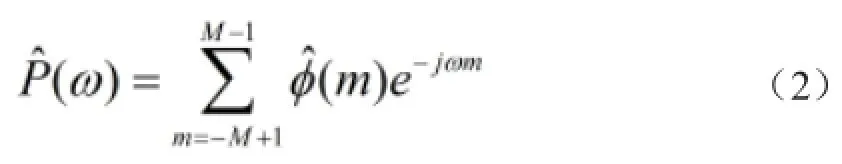
利用窗函数，式（2）又可表达为

式中，WM（m）为窗函数，窗函数可以选取为矩形窗、Hamming窗等，窗函数选取不同对谱估计性能的影响也不同。

2.2周期图方法

周期图方法［8］对信号x（n）的功率谱估计为

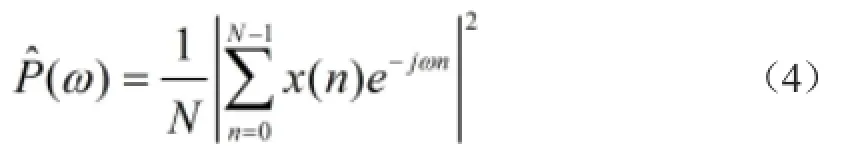
将长度为N的平稳随机信号序列x（n）分成K段，每段长度为L，即L=N/K，第i段序列为

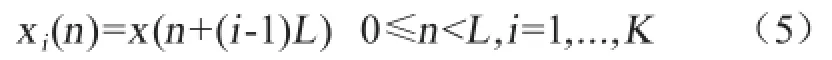
计算周期图之前，先用窗函数WL（n）给每段序列xi（n）加权，K个修正的周期图定义为

式中，U表示窗函数序列WL（n）的能量

功率谱估计为

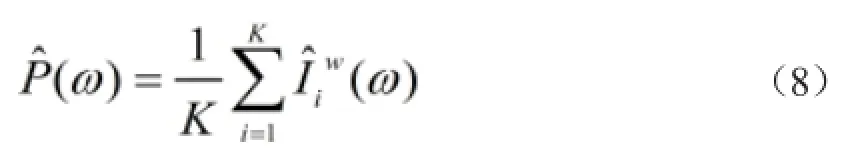
3　仿真分析

利用自相关函数法和周期图方法对下面受噪声干扰的正弦信号进行谱估计

式中，NS为正弦个数；和 αi分别为第i个正弦信号的数字频率、相位和幅度，随机的分布在［0，2π）之间；w（n）为零均值方差等于的复高斯白噪声。

（1）两种谱估计方法比较

用Matlab对两种谱估计方法进行仿真，其中，N=100，M=10，NS=1，ω1=0.6π，，选择矩形窗。与自相关函数法的谱估计相比，周期图法旁瓣幅度显著减小，稳定性提高，但是分辨率比自相关函数法低。

图1　两种方法下的功率谱估计曲线

（2）窗长度M对谱估计性能的影响

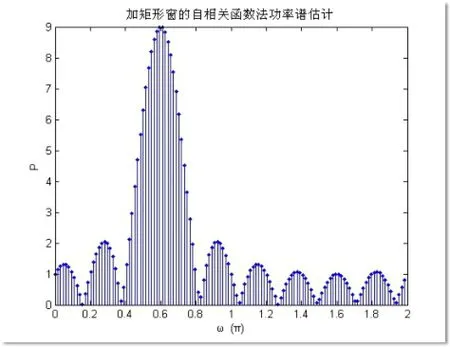
图2　M=5时自相关函数法功率谱估计曲线

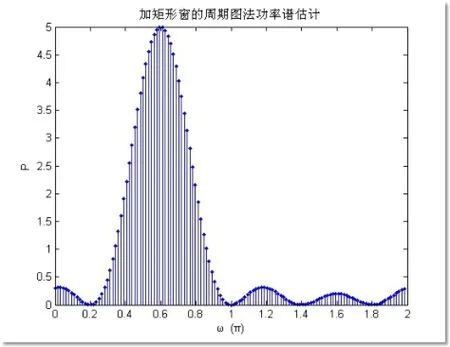
图3　L=5时周期图法功率谱估计曲线

比较窗长度M（或L）为10和5时的仿真结果，即对比图2和图1（a），图3和图1（b），可以看出，两种方法均随着窗长度的减小主瓣宽度变宽，分辨率降低；旁瓣振荡频率降低，旁瓣数目减少；幅度整体降低，但主瓣与旁瓣的相对比例基本没有改变。

（3）窗函数对谱估计性能的影响

以自相关函数法为例分析窗函数对谱估计性能的影响。

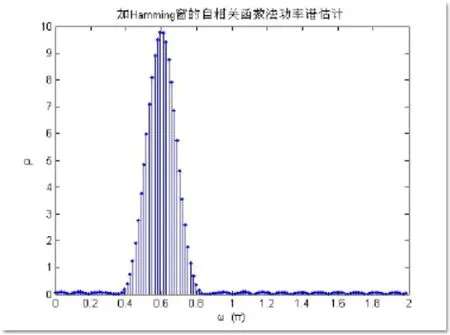
图4　加Hamming窗的自相关函数法功率谱估计曲线

与图1（a）的矩形窗相比，Hamming窗功率谱的旁瓣幅度大大降低，起到了对旁瓣的抑制作用，但付出的代价是主瓣宽度增加了近一倍，分辨率降低。

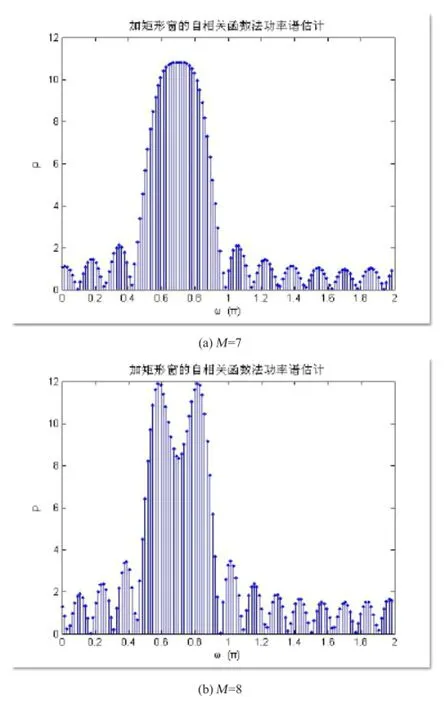
图5　调整M时加矩形窗的自相关函数法功率谱估计曲线

为比较分辨率，输入N=100，NS=2，ω1=0.6π，选择矩形窗，调整自相关序列长度M，观察分开两个正弦分量的临界M值。

图6　调整M时加Hamming窗的自相关函数法功率谱估计曲线

观察图6可知，加矩形窗时，M=8时可将两个正弦频率分量临界分辨出来，加Hamming窗时，M=10时可将两个正弦频率分量临界分辨出来。可见Hamming窗使得功率谱的主瓣变宽，分辨率下降。

（4）信噪比对谱估计性能的影响

对比图1（a） 时，增大白噪声的方差时，对主瓣没有产生影响，但是旁瓣的宽度和幅值稍有增大，使得旁瓣和主瓣的幅度比变大。可见信噪比的降低会对谱估计产生不利影响。

图7　时加矩形窗的自相关函数法功率谱估计曲线

4　结束语

两种经典谱估计方法均能准确的估计出谱峰位置，周期图法较自相关函数法稳定性提高但分辨率下降。在同一种谱估计方法下，旁瓣与主瓣的相对关系只取决于窗口的形状。窗长度的减小会造成主瓣宽度增大，分辨率降低，旁瓣的振荡频率减小，但主瓣与旁瓣的相对比例没有改变。在实际工程应用中应根据需要选取合适的谱估计方法以及窗函数。

［1］吴兆熊，黄振兴，黄顺吉.数字信号处理 下册［M］.北京：国防工业出版社，1988

［2］Wang Guolin，Liu Yongchen. The methods of power spectrum estimation based on measured pavement［C］. International Conference on Electric Information and Control Engineering，2011，P2787-2790

［3］Yao Yu，Heming Zhao. A new method for noise power spectrum estimation［C］. 4th IET International Conference on Wireless，Mobile & Multimedia Networks，2011，P206-209

［4］蒋宇中，刘月亮，应文威.短波信道多普勒功率谱密度研究［J］.电波科学学报，2013，28（4）: 775-781

［5］Petre Stoica，Randolph L. Moses. Spectral Analysis of Signals［M］. Pearson Prentice Hall，2005

［6］John G. Proakis，Dimitris G. Manolakis. Digital Signal Processing-Principles，Algorithms，and Applications （Fourth Edition） ［M］. Prentice Hall，2007

［7］王立琦，王铭义，张礼勇，江连洲，于殿宇.谱估计中解析公式与卡尔曼滤波比较研究［J］.哈尔滨工程大学学报，2010，31（1）: 115-119

［8］余训锋，马大玮，魏琳.改进周期图法功率谱估计中的窗函数仿真分析［J］.计算机仿真，2008，25（3）: 111-114

Study of Classic Power Spectrum Estimation Method

Ju Ying，He Jia，Hu Jixin
（State Radio Monitoring Center Shaanxi Monitoring Station，xi’an，710200）

This paper is aimed at power spectrum density，which is the most important statistical characterization in random signal processing. The classic power spectrum estimation method，including the autocorrelation function method and the periodogram method are studied. Through simulation，the performances of these methods are analyzed. The performances of spectrum estimation under the influence of window length，window function and signal to noise ratio are studied. It provides evidence for the selection of spectrum estimation method and parameters in engineering applications.

power spectrum density； autocorrelation function method； periodogram method； resolution

10.3969/J.ISSN.1672-7274.2015.04.012

TN98

A

1672-7274（2015）04-0047-04