基于MATLAB实现的AR模型功率谱估计

刘明晓，王旭光

（1.西安铁路职业技术学院 陕西 西安 710014；2.西安航天自动化股份有限公司 陕西 西安 710014）

基于MATLAB实现的AR模型功率谱估计

刘明晓1，王旭光2

（1.西安铁路职业技术学院 陕西 西安 710014；2.西安航天自动化股份有限公司 陕西 西安 710014）

现代功率谱估计和经典功率谱估计是两种常用的功率谱估计，同时也是分析随机信号的常用方法。本文详细介绍了现代功率谱估计中有关AR模型参数的功率谱估计，具体包括自相关算法、Burg算法、协方差算法以及改进的协方差算法，在此基础上又对四种不同功率谱估计方法的性能指标进行了比较分析。在MATLAB仿真软件平台上对AR模型参数的四种不同功率谱估计算法进行了仿真，同时对功率谱估计结果进行了分析比较并得到了预期的谱估计效果。最后从实际应用角度出发讨论了AR模型参数不同功率谱估计算法的特点，以便在应用中能够选择合适的功率谱估计算法。

功率谱估计；AR模型；算法；MATLAB

在频谱分析中功率谱估计是常被采用的一种重要方法，功率谱估计广泛应用于人们的日常生活、声纳、生物医学、雷达以及农业活动等不同领域的信号处理过程中[1-2]。如何从频带较宽的信号中检测出频带较窄的信号也是功率谱估计在信号处理中的重要应用[3]。此外功率谱估计是用有限长的数据来对信号进行功率谱估计，是分析随机信号时常被采用的一种重要方法。

为了能够良好地解决经典功率谱估计 （包括自相关法和周期图法）中方差性能不好以及分辨率较低等问题提出了现代功率谱估计[4]，其涉及的领域以及学科相当广泛且内容比较丰富[5]。现代功率谱估计包括非参数模型估计和参数模型估计两种，前者有最小方差法，多分量的MUSIC方法等；后者有AR模型、MA模型、ARMA模型、PRONY指数模型等[6-7]。文中对现代功率谱估计中有关AR模型参数的几种典型求解算法进行分析比较，同时在MATLAB仿真软件平台上对AR模型参数中不同算法的功率谱估计进行了仿真，最后从实际应用的角度出发讨论了不同功率估计算法的特点，以便在实际应用中能够选择最合适的功率谱估计算法[8]。

1 现代功率谱估计

现代功率谱估计又称参数谱估计[9]，是先对数据进行观察后再进一步对参数模型进行估计，然后根据得到参数模型输出的功率来对信号进行谱估计。采用现代功率谱估计能够较好地改善经典谱估计中方差性能差以及分辨率低等问题[10]。现代功率谱估计中AR模型是应用较多的一种模型。

1.1 AR模型的建立

AR模型是全极点模型同时又称为自回归模型[11]。可用公式（1）所示的差分方程来描述：

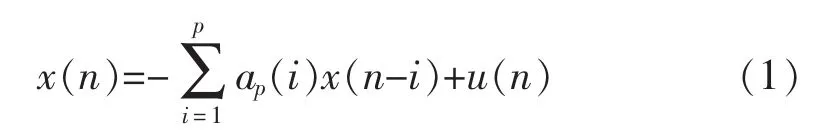
其中u（n）是一个白噪声序列，其均值为0、方差为 σ2，p 是 AR 模型的阶数，ap（i），i=1，2，…，p。AR 模型系统的转移函数H（z）为：

由公式（1）和公式（2）可得到AR模型参数的功率谱估计计算公式：

AR模型的参数和x（n）自相关函数有如下的关系：

将上式写成矩阵的形式：

式（5）为AR模型的正则方程，又称尤拉-沃克（Yule-Walker）方程[12]。

1.2 AR模型参数估计的典型算法

1.2.1 自相关法

自相关法是AR模型参数估计中较为简单的一种功率谱估计方法。按照模型阶数由小到大的顺序进行计算，先计算阶次 m=1 时的系数 am（k）=a1（1）和，再计算 m=2 时的 a2（1），a2（2）和，按此方法依次计算到阶次 m=p 时的 ap（1），ap（2），…，ap（p），及，当的精度满足要求时即可停止。递推公式为：

1.2.2 Burg算法

Burg算法进行功率谱估计时其前后项序列误差的前后都不加窗，使用Levinson-Durbin递推可快速求解AR模型参数的系数。

Burg算法与自相关算法不同之处在于使序列x（n）的前后项功率预测误差之和：

再根据Levinson-Durbin进行递推得出AR模型系数如下：

Burg算法不需先计算自相关函数进而计算速度有所提高同时计算也相对简单。与自相关算法相比分辨率也有所提高。但在处理白噪声加正弦信号时功率谱线会出现分裂现象。

1.2.3 协方差算法

协方差算法与其他算法的不同之处在于预测误差功率求和的上下限取值范围不同。在协方差算法区间[0，N-1]外 x（n）样本不为 0，故表达式中的 x（n-k）总是落在区间[0，N-1]中，因此预测误差功率求和的上下限必然会落在[p，N-1]之间。得到的矩阵是半正定矩阵，且不具有Toeplitz性质，故不能采用Levinson-Durbin递归算法进行参数求解，同时得到的AR模型也不稳定。

1.2.4 改进协方差算法

采用改进的协方差算法进行功率谱估计时，为了使前后项功率误差之和最小其前后项都不加窗，得到的协方差矩阵不是Toeplitz矩阵，故不能用Levinson递推算法对模型参数进行求解。Marple在1980年提出了改进协方差方程求解的快速算法，该算法能够大大提高功率谱估计的性能。

1.3 用于功率谱估计的数据

文中采用由复数噪声加上4个复正弦组成的数据对功率谱进行估计。其中归一化频率分别是f1=0．15，f2=0．16，f3=0．252，f4=-0．16。 该数据的 128 点复序列如图1所示。

图1 功率谱估计数据

2 AR模型功率谱估计的MATLAB仿真

借助MATLAB对AR模型功率谱进行估计时，上述4种算法分别采用pyulear函数、pburg函数、pcov函数和pmcov函数来完成功率谱估计。分别用这4个函数对图1中的随机序列进行功率谱估计便可得到相应的功率谱线。图2～4是自相关算法得出的阶次p分别为10，20和30时的AR模型功率谱曲线。

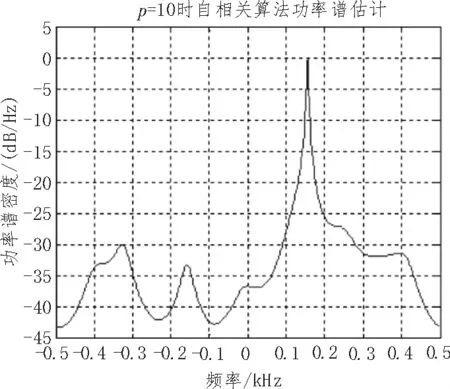
图2 阶次p=10时自相关算法功率谱估计

从图2～4的功率谱估计图形可以得出，在阶次p较低时 （如图2所示）功率谱估计的分辨率不理想。当阶次p提高到30时，在频率f1和f2处两个正弦信号刚好被分离开，在频率f3和f4处也能够分离出两个正弦信号。在自相关算法中由于对序列的前后项加窗降低了分离效果，数据越短分离效果越不好。

图3 阶次p=20时自相关算法功率谱估计

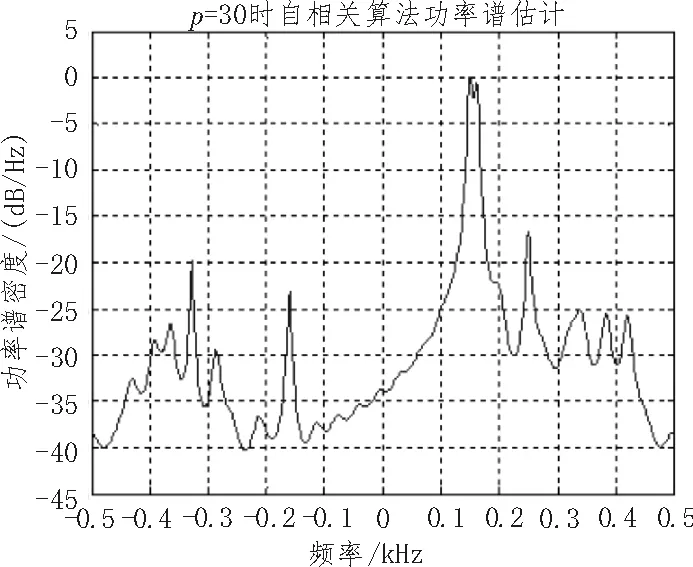
图4 阶次p=30时自相关算法功率谱估计

图5～图6是Burg算法对随机数列信号进行功率谱估计时的功率谱曲线。

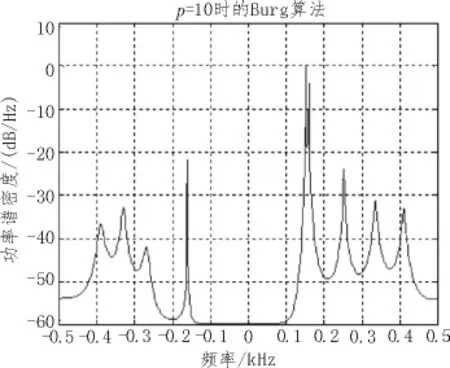
图5 阶次p=10时Burg算法功率谱估计

图6 阶次p=15时Burg算法功率谱估计

比较分析图5和图6可以得出在阶次p=15时得到了较好的谱估计。另外对比图4和图5可以看到Burg算法的分辨率明显优于自相关算法，在阶次较低时（如图5所示）也能较好地分辨出间隔较小的频率点。

图7为阶数p=10时协方差算法对随机数列信号进行估计得到的功率谱曲线。

图7 阶次p=10时协方差算法功率谱估计

从图7可得出功率谱估计在信号源频率f1=0．15，f2=0．16，f3=0．252，f4=-0．16 处功率谱线相对较窄，在其他频率处功率谱线起伏剧烈。采用协方差算法对功率谱进行估计能够较真实地反映信号实际模型。

图8～图9是阶数p=10和p=15时改进的协方差算法得出的AR模型功率谱估计曲线。

图8 阶次p=10时改进协方差算法功率谱估计

图9 阶次p=15时改进协方差算法功率谱估计

比较图7～图9可以得出两种协方差算法的功率谱估计大致相同，但改进的协方差算法在信号频率处的峰值更加尖锐、更加突出且更有利于辨识。分析图8和图9可以得出在阶次较高时能得到非常满意的功率谱估计曲线。

3 结 论

文中介绍了现代功率谱估计中AR模型参数的几种功率谱估计算法。其中自相关算法需要对前项预测的误差序列前后加窗，加窗降低了自相关算法的分辨率，数据越短分辨率越低。与自相关算法相比Burg算法有较好的分辨率，但有时会出现谱估计曲线分裂现象。改进的协方差算法性能最好，但计算与编程都相对繁琐。在对功率谱进行估计时，需要依据实际数据序列选择更合适的算法进行功率谱估计。

[1]邓泽怀，刘波波，李彦良．常见的功率谱估计方法及其Matlab仿真[J]．电子科技，2014（2）:50-52．

[2]李军，王凯．三种现代功率谱估计方法性能研究[J]．科技信息，2010（30）:554-555．

[3]李文超．现代功率谱估计在设备故障诊断应用[J]．传感器世界，2012（2）:25-29．

[4]王春兴．基于Matlab实现现代功率谱估计[J]．现代电子技术，2011，34（16）:65-67．

[5]范泽华，白铁成．基于改进差分演化的高效图像分割算法[J]．现代电子技术，2016，39（14）:87-91．

[6]杨蓉．多普勒雷达测速系统设计及信号处理方法研究[D]．武汉：华中科技大学，2012．

[7]汪胜波．功率谱估计在宽带ADCP信号检测中的研究与应用[D]．青岛：中国海洋大学，2011．

[8]闫庆华，程兆刚，段云龙．AR模型功率谱估计及Matlab实现 [J]．计算机与数字工程，2010，38（4）:154-156．

[9]郭会娟．基于AR参数模型和小波分析的电机故障诊断[D]．郑州：华北水利水电大学，2013．

[10]崔晓荣．电力系统间谐波的检测算法研究与实现[D]．成都：西华大学，2013．

[11]张峰，伊丽，石现峰．振动信号的最小方差谱估计算法[J]．计算机技术与发展，2015（10）:76-79．

[12]袁华，赵越，蔺永政，等．基于最小方差的功率谱估计方法的研究[J]．数字通信世界，2015（9）:254-255．

The realization of AR model power spectrum estimation based on MATLAB

LIU Ming-xiao1，WANG Xu-guang2
（1.Xi'an Railway Vocational&Technical Institute，Xi'an 710014，China； 2.Xi'an Aerospace Automation CO，.LTD.，Xi'an 710014，China）

Power spectrum estimation can be divided into modern spectral estimation and classical spectral estimation，it is an method for analyzing random signal.It describes the autocorrelation algorithm，Burg algorithm，covariance algorithm and improved covariance algorithm of AR model parameters in Modern Spectral Estimation，and their perform indicators are analyzed in this paper.These methods for AR model parameter algorithm are implemented by MATLAB，the results of simulation are analyzed and get a better spectrum estimation.Moreover，the advantages and disadvantages of these methods are discussed from the experimental view so as to make reasonable selection in practical work.

PSD estimation； AR model； algorithm；MATLAB

TN015

A

1674－6236（2017）17-0129-04

2016-07-23稿件编号：201607167

刘明晓（1987—），女，河南焦作人，硕士，助教。研究方向：电力系统及其自动化。