直升机地面开车过程旋翼／机体／起落架耦合气弹动力学分析

侯 鹏，杨卫东，孙东红，黄斌根，董凌华

（1．南京航空航天大学直升机旋翼动力学国家重点实验室，江苏 南京 210016；2．中国直升机设计研究所，江西 景德镇 333001）

引 言

直升机在地面开车过程中，旋翼转速的变化会引起惯性力及气动力的动态变化，通常直升机地面开车试验旋翼拉力变化范围为0＜T／G≤0．9，其中G为全机重量［1］。为模拟直升机在离地前的动态过程，需建立旋翼／机体／起落架耦合气弹动力学模型。目前中国直升机设计部门所采用的二维及三维工程模型通常将桨叶减摆器及起落架刚度与阻尼特性等效处理为线性［2，3］，并在建模中截掉高阶项与简化各种非线性项的影响；进一步发展的旋翼／机体耦合气弹模型考虑了旋翼的入流及气动力影响，利用线化小扰动动力学方程进行稳定性研究［4，5］。工程上的线性模型及线化小扰动方法只能进行稳定性分析，无法对直升机地面开车过程进行动态分析研究。

由于在地面开车过程中旋翼的惯性力及气动力的动态变化，基于线性系统的小扰动线化方法已不适合进行直升机地面开车的仿真模拟分析。在旋翼／机体／起落架耦合非线性气弹动力学模型中，旋翼的挥舞、摆振自由度以及机体自由度在计算中未进行小角度假设，并在运动学描述中保留所有非线性项及高阶项的影响，各片桨叶及起落架的特性（包括刚度、阻尼、惯量等特性）均独立赋值，并可设为时间与位移的函数形式，将起落架和减摆器的实测数据作为特性输入，用于模拟动力学部件的非线性、各种不平衡以及结构意外破坏等现象。考虑机体重心的提升及起落架伸长的影响，在直升机旋翼起动过程中，机体及桨叶的运动与旋翼气动载荷密切相关，在气动力建模中，引入动力入流及非定常气动力模型，用于模拟旋翼起动过程气动非定常特性。

1 建 模

1．1 动力学建模

在旋翼／机体／起落架耦合气弹动力学模型中，机体及桨叶都采用刚体假设，桨叶运动考虑挥舞和摆振自由度，机体考虑6个自由度（包括3个平动自由度和3个转动自由度）。起落架的刚度、阻尼特性以及桨叶摆振刚度和阻尼均可考虑非线性影响。旋翼／机体／起落架耦合气弹动力学结构模型，简化如图1所示。

如图1所示，为描述空间运动关系，模型定义6个坐标系，分别为惯性坐标系，下表为i；以机体重心为原点，定义机体坐标系，下标为f；以桨毂中心为原点，定义桨毂坐标系，下标为h；旋转坐标系，下标为r；以挥舞铰为原点，定义桨叶挥舞坐标系，下标为β；以摆振铰为原点，定义桨叶摆振坐标系，下标为ζ。

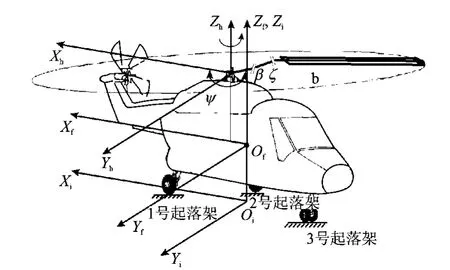
图1 模型结构示意图Fig．1 Model structural figure

根据广义Hamilton原理，表达式如下

式中δUbk为第k片桨叶势能变分；δULj为第j号起落架势能变分；δTbk为第k片桨叶动能变分；δTf为机体动能变分；δWbk为第k片桨叶虚功，包括减摆器阻尼力及气动力虚功影响；δWLj为第j号起落架阻尼力虚功；δWG为机体重力虚功。

1．1．1 桨叶建模

根据坐标系定义，第k片桨叶任意剖面质心在惯性系下的位置矢量［6，7］

式中Tif为机体坐标系到惯性坐标系转换矩阵；Tfh为桨毂坐标系到机体坐标系转换矩阵；Thr为旋转坐标系到桨毂坐标系转换矩阵；Trβ为挥舞坐标系到旋转坐标系转换矩阵；Tβζ为摆振坐标系到挥舞坐标系的转换矩阵。｛xcg，ycg，zcg｝T为机体重心在惯性坐标系的坐标，｛xhyhzh｝T为桨毂中心在机体坐标系下的坐标。将惯性坐标系下的位置矢量Rbi对时间求一次导数和二次导数，分别得出该点在惯性坐标系下的速度和加速度：

通过沿桨叶展向积分，可得出第k片桨叶动能及其变分为：

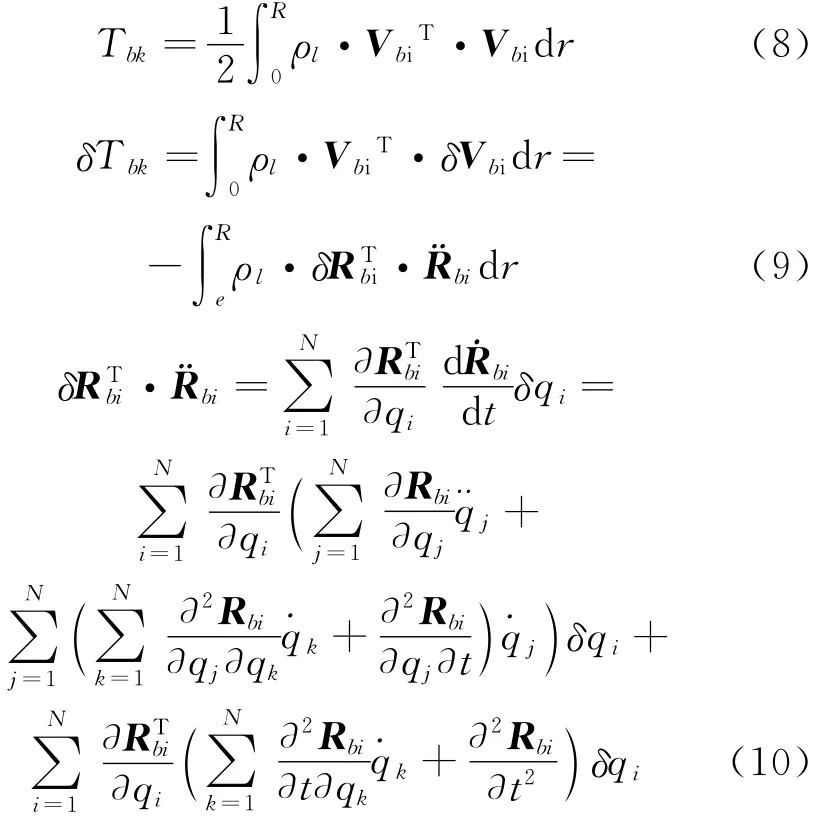
根据式（10）得到桨叶动能表达式所产生的质量阵与阻尼阵以及广义力阵均是随时间变化的，对旋翼与机体的转动自由度均不做小角度假设，在瞬态响应计算中，不做线化处理，保留所有非线性项与高阶项的影响。

为方便各片桨叶动能求和，将旋转坐标系下定义的挥舞、摆振自由度向不旋转坐标系下定义的旋翼整体振型自由度转换［8］，以挥舞为例具体表示如下

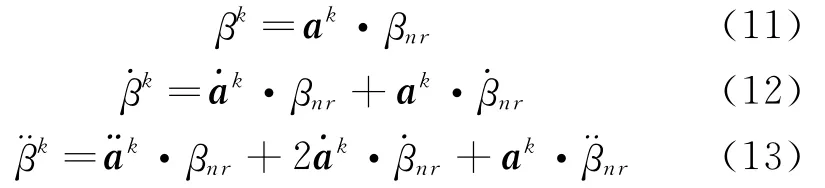
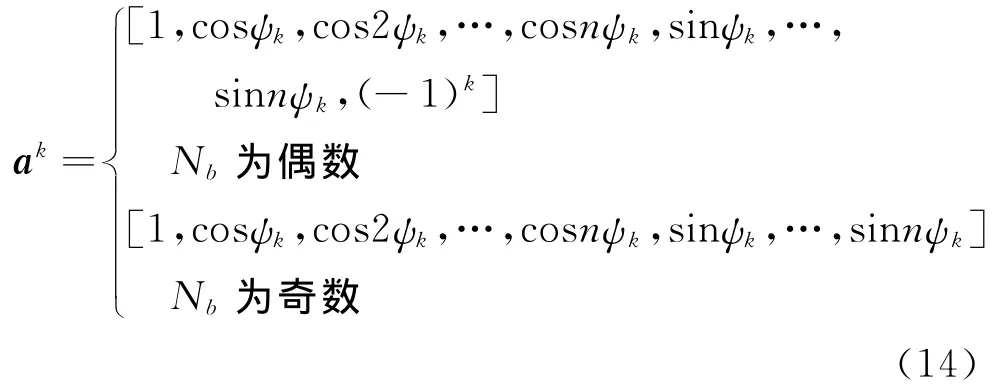
式中Nb为桨叶片数，ψk为第k片桨叶的方位角，

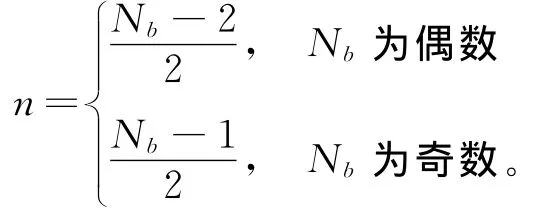
1．1．2 机体建模

机体坐标系原点定义在机体重心，坐标轴正方向定义如图1所示。Tθx，Tθy和Tθz分别为机体滚转、俯仰、偏航坐标系的转换矩阵。

机体坐标系到惯性坐标系的转换矩阵为

取机体上任意点在机体坐标系下的坐标为：｛xf，yf，zf｝T，该点在惯性坐标系下位置矢量为

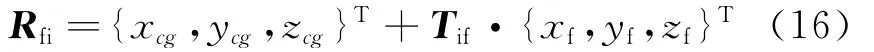
式中 ｛xcg，ycg，zcg｝T为机体重心在惯性坐标系下的坐标。

该点在惯性系中速度矢量为

该点动能及其变分为：

对机体积分得到机体动能变分为

机体重力虚功为

式中M为机体质量。

1．1．3 起落架影响

旋翼起动过程中，随旋翼拉力增加，机体重心提升，起落架会伸长，运动过程简化如图2所示。

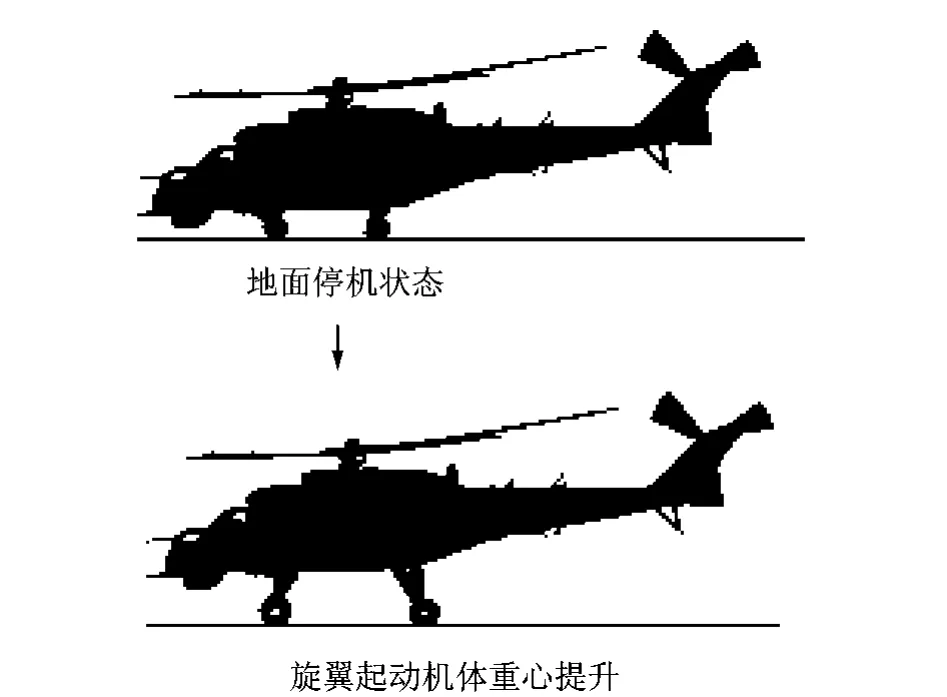
图2 旋翼起动过程起落架伸长示意图Fig．2 Schematic diagram of landing gears elongation during rotor starting process on ground

第j号起落架着地点在惯性系下位置向量为

第j号起落架弹性支柱机身作用点在惯性系下位置向量描述为

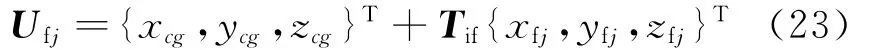
式中 ｛xfj，yfj，zfj｝T为第j号起落架弹性支柱在机体上的作用位置。

第j号起落架位置矢量

第j号起落架长度

第j号起落架伸长量：ΔLj＝Lj0－Lj，Lj0为起落架在完全放松情况下的自由长度，当ΔLj为负时，表明起落架长度大于完全放松情况下的自由长度，说明该起落架已离开地面，这时起落架不起作用，机体的约束条件也发生改变。

实际上，起落架刚度、阻尼均是压缩量的函数。阻尼力根据实测数据，表示为压缩量的函数形式FC（ΔLj，Δ˙Lj）。根据实测刚度特性，弹性力计算如下

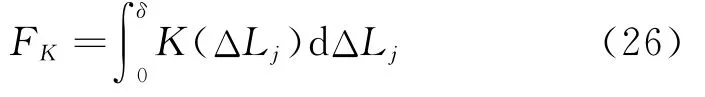
1．2 气动力建模

旋翼入流模型采用动力入流模拟［2，9］，入流方程如下

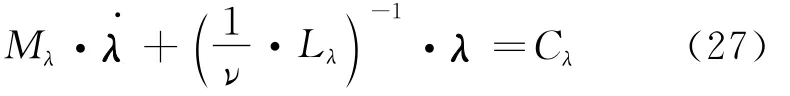
桨盘上任意点入流表示如下

采用Leishman－Beddoes非定常气动模型计算桨叶剖面非定常气动力［10，11］。

Leishman－Beddoes模型的状态方程可表示为：

式中α和q分别表示桨叶剖面迎角和变距速率；Cc为弦向力系数，αE为剖面有效迎角，f″为后缘分离点，为考虑后缘分离的非线性法向力为涡升力。

桨叶的剖面气动力为：

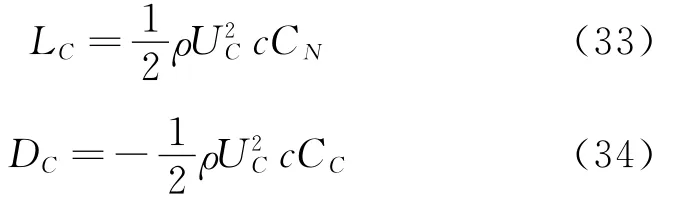
忽略桨叶径向气动力的影响，将剖面气动载荷转到惯性坐标系，表示如下

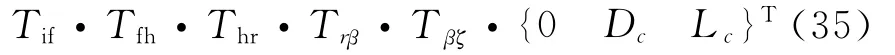
将剖面气动力虚功沿桨叶展向积分得到第k片桨叶气动虚功表达式如下

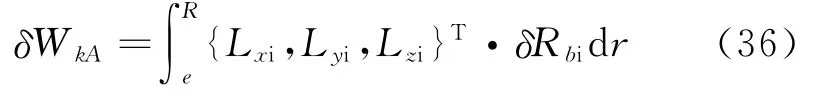
2 计算分析

根据某型直升机相关参数进行算例计算。基本参数由表1给出。

表1 基本参数表Tab．1 Basic parameter table

实际起落架、减摆器等刚度、阻尼特性均是非线性的，通常为压缩量的函数。表1中的起落架刚度为起落架的等效线性刚度，实际起落架Z向的刚度可以用实测数据作为特性输入［1］，如图3所示。

2．1 旋翼变转速定总距起动响应分析

旋翼起动过程，假定旋翼转速连续的操纵变化规律由图4给出。

在图4示的转速变化规律下，在3种不同总距下起动旋翼，单片桨叶摆振及挥舞自由度响应对比由图5和6给出。

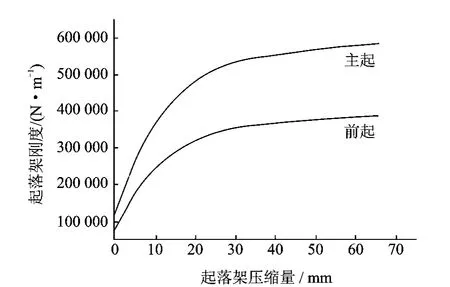
图3 起落架Z向刚度特性Fig．3 Stiffness property of landing gears on Zdirection

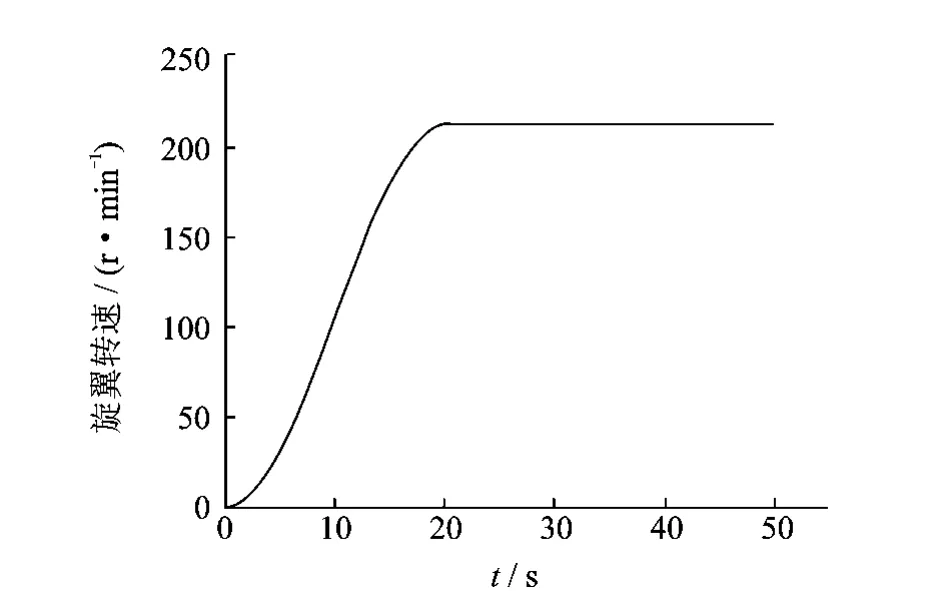
图4 旋翼转速变化规律Fig．4 Variation regulation of rotor speed

图5 不同总距下旋翼起动过程单片桨叶摆振响应Fig．5 Lag response of blade in different collective pitch controls during rotor starting process on ground

图6 不同总距下旋翼起动过程单片桨叶挥舞响应Fig．6 Flap response of blade in different collective pitch controls during rotor starting process on ground

由图4转速变化规律可知，旋翼转速处于动态变化过程中，旋翼转速的加速度在转速变化的起始点和终止点均为零，加速度呈现先增大后减小的规律。由图5和6可知，采用较大总距起动时，会引起桨叶较大的摆振和挥舞过冲响应。采用低总距起动，能有效降低旋翼起动过程的桨毂载荷。以固定桨距起动，桨叶受转速加速度引起的惯性力的影响，在旋翼变转速阶段，桨叶摆振响应呈现先增大再减小的趋势，这与转速加速度变化规律一致。在图4的旋翼转速变化规律下，由于旋翼转速变化始终是连续的，因此旋翼挥舞与摆振响应在旋翼转速恒定后，能较快进入恒定值。如果旋翼转速采用固定变化率进行线性变化，由于在初始和结束时刻，旋翼转速变化率不连续，会因为惯性作用导致桨叶响应有一个明显振荡衰减过程。

在图4所示的转速操纵规律下，机体响应由图7～9给出。

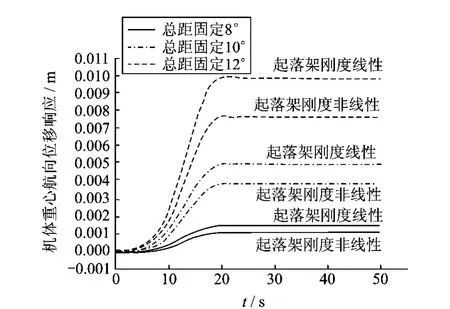
图7 不同总距下旋翼起动过程机体重心航向位移响应Fig．7 Directional displacement response of fuselage centre of gravity in different collective pitch controls during rotor starting process on ground

由于桨叶剖面气动力与转速有关，跟随旋翼转速进行动态变化，由图8可以看出，以固定桨距起动过程中，机体质心在逐渐增大的旋翼转速引起的气动力的作用下逐渐提升。由图7～9分析结果可以看出直升机瞬态响应分析模型分别采用非线性刚度与等效线性刚度的计算结果差别较大，由于非线性刚度的特性是通过实测得到的，更接近真实直升机起落架的刚度特性。因此相对于等效线性刚度的计算分析结果能够更好地反映真实情况下直升机地面工作情况，这种差别也有助于提醒直升机设计人员在未来建模分析中应适当考虑结构参数非线性的影响。

图8 不同总距下旋翼起动过程机体重心提升位移响应Fig．8 Vertical displacement response of fuselage centre of gravity in different collective pitch controls during rotor starting process on ground

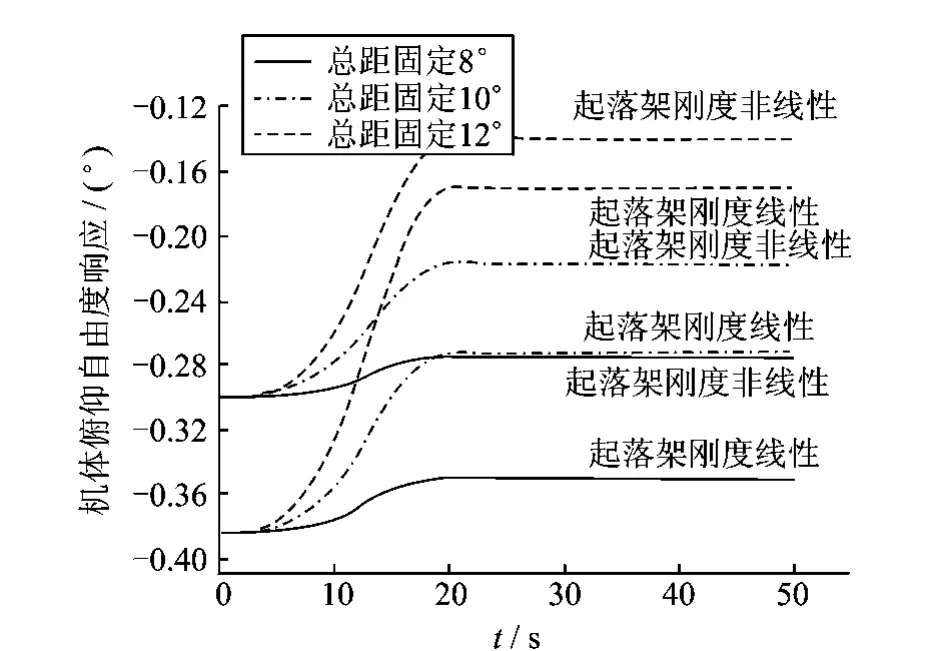
图9 不同总距下旋翼起动过程机体俯仰自由度响应Fig．9 Fuselage pitch response in different collective pitch controls during rotor starting process on ground

2．2 旋翼变转速变总距起动响应分析

为降低桨叶在起动过程中的过冲响应，改善桨毂载荷环境，可以缓慢提高总距起动旋翼。在图4所示旋翼转速变化规律下开车，20s内总距提高4°。单片桨叶摆振与挥舞响应对比分别由图10和图11给出。起落架刚度特性采用如图3所示的非线性模型，机体响应由图12～14给出。

由图10和11分析结果可知，采用较大总距起动时，会引起桨叶较大的摆振、挥舞过冲响应。采用低总距起动，能有效降低旋翼起动过程的桨毂载荷。旋翼起动过程中，通过缓慢提高桨叶总距这种折中的方式可有效降低桨叶摆振幅值和挥舞过冲响应，改善桨毂载荷环境。

图10 变转速变总距下旋翼起动过程单片桨叶摆振响应Fig．10 Lag response of blade in variable collective pitch control and rotor speed during rotor starting process on ground

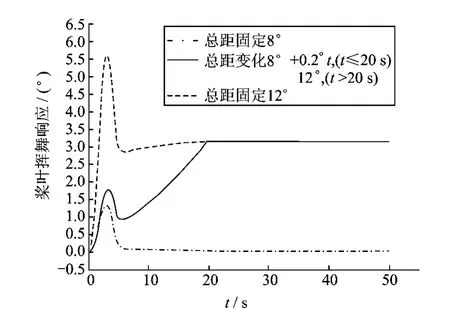
图11 变转速变总距下旋翼起动过程单片桨叶挥舞响应Fig．11 Flap response of blade in variable collective pitch control and rotor speed during rotor starting process on ground

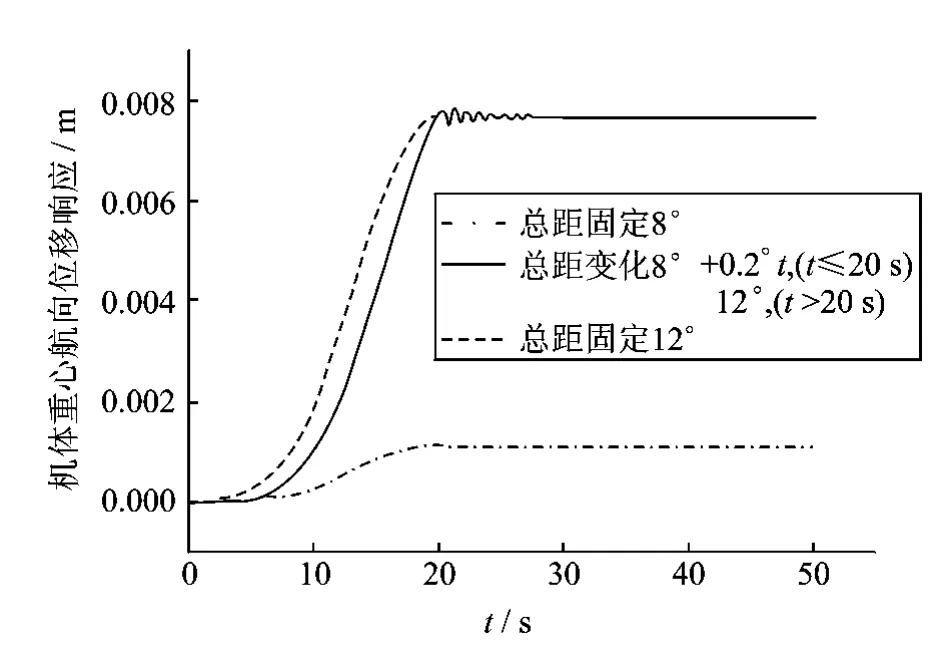
图12 变转速变总距下旋翼起动过程机体重心航向位移响应Fig．12 Directional displacement response of fuselage centre of gravity in variable collective pitch control and rotor speed during rotor starting process on ground

图13 变转速变总距下旋翼起动过程机体重心提升位移响应Fig．13 Vertical displacement response of fuselage centre of gravity in variable collective pitch control and rotor speed during rotor starting process on ground

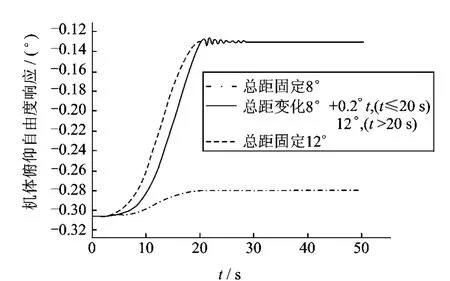
图14 变转速变总距下旋翼起动过程机体俯仰自由度响应Fig．14 Fuselage pitch response in variable collective pitch control and rotor speed during rotor starting process on ground

2．3 旋翼起动过程意外情况模拟

针对旋翼起动过程可能发生的意外情况，对桨叶与机体响应进行模拟。直升机旋翼的减摆器能为桨叶提供摆振铰簧刚度并为避免动力学不稳定现象提供足够的摆振阻尼。减摆器长期使用会磨损，损坏失效概率也较大。通过将摆振刚度与摆振阻尼设置为远低于其额定值来模拟减摆器失效时的情况。现假设旋翼起动10s后，旋翼总距为12°时，1号桨叶减摆器失效，当响应达到稳态振动后，失效桨叶r／R＝0．707处剖面升力系数由图15给出，失效桨叶挥舞、摆振响应由图16给出，未失效桨叶挥舞、摆振响应分别由图17和18给出。

图15 失效桨叶剖面升力系数Fig．15 Failure blade section lift coefficient

图16 失效桨叶挥舞摆振响应Fig．16 Flap and lag response of failure blade

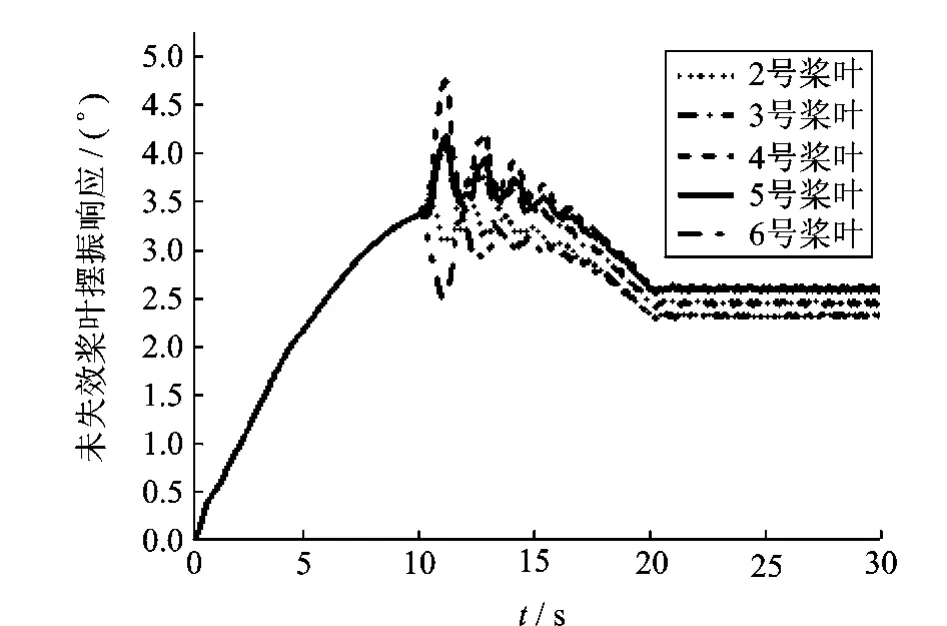
图17 未失效桨叶摆振响Fig．17 Lag response of other normal blades

由图15可以看出，当某片桨叶减摆器突然失效后，由于失效桨叶摆振自由度的约束条件突然发生改变，旋翼桨盘产生质量偏心，在气动阻尼的作用下，失效桨叶会进入稳定周期振动。由于采用非定常气动模型，因此在桨叶产生非定常运动时，桨叶剖面的非定常气动特性得以体现。由图16～18结果可以看出，当减摆器失效时，旋翼／机体耦合系统会发生剧烈振动，由于旋翼气动阻尼的存在，桨叶振动会逐渐进入稳定振动状态。某片桨叶的减摆器失效导致桨盘出现质量偏心。在这种动不平衡的作用下，旋翼／机体耦合动力学系统始终受到1Ω的离心力的激励，各自由度最终均进入稳定周期振动状态。

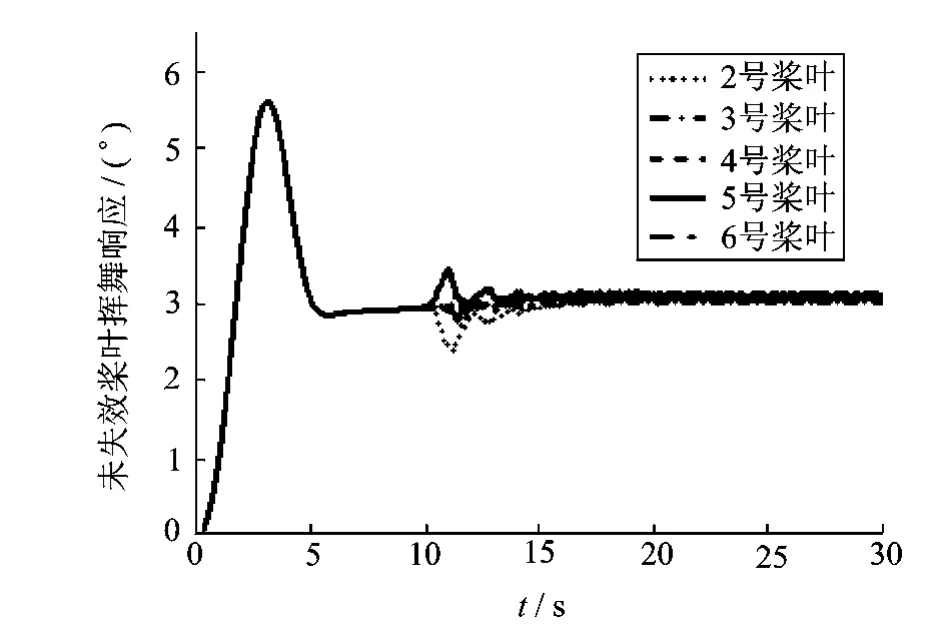
图18 未失效桨叶挥舞响应Fig．18 Flap response of other normal blades

桨叶振动载荷通过桨毂传至机身，引起机身振动。桨叶减摆器失效，旋翼平面内激振力主要对机体航向、横向平动自由度以及俯仰、滚转2个转动自由度运动产生较大影响。直升机体的加速度响应会直接影响机载设备与仪表的正常工作，以及驾驶员的驾驶疲劳程度，因此机体振动的加速度水平一直都是设计人员要考虑的重要问题。机体加速度响应，由图19～22给出。

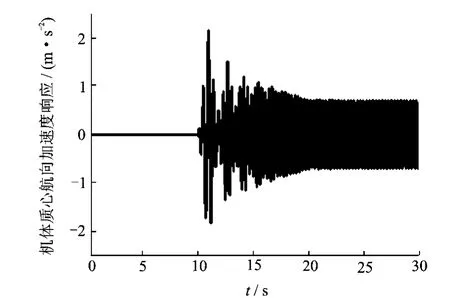
图19 机体质心航向加速度响应Fig．19 Directional displacement acceleration response of fuselage centre of gravity

由图19～22可知，由于失效桨叶摆振铰簧刚度降至较低水平，因此，在减摆器残余刚度与离心刚度的作用下桨叶以较低频率衰减至稳态。在减摆器失效桨叶摆振响应达到稳定周期振动之前，可明显看出机体受到桨叶低频摆振激励的影响，同时也会受到与转速相关的质量偏心的影响，可以看出在机体低频振动的响应中叠加有高频信号。当旋翼转速达到额定转速后，旋翼／机体系统受旋翼偏心的影响，均以1Ω频率进行稳态振动。当桨叶减摆器失效后，在旋翼对机体周期激励下，机体振动水平会明显升高，会对驾驶员的驾驶以及一些仪表的正常工作产生影响。

图20 机体质心横向加速度响应Fig．20 Lateral displacement acceleration response of fuselage centre of gravity

图21 机体滚转自由度加速度响应Fig．21 Roll acceleration response of fuselage

图22 机体俯仰自由度加速度响应Fig．22 Pitch acceleration response of fuselage

2．4 地面开车瞬态响应稳定性判断

特征值分析和瞬态响应分析是稳定性分析的两种典型方法。用特征值分析直升机“地面共振”稳定性是基于线化处理的分析方法。利用瞬态响应分析方法可以在模型中充分考虑各动力学单元的非线性特性。基于原准机数据，利用线化进行特征值分析，图23为直升机旋翼／机体／起落架耦合系统的特征值实部，用于反映系统各模态的阻尼特性，实部为正值表明系统在该转速下发生不稳定。原准机在全转速范围内无不稳定区。X，Y和Z分别为机体航向、横向和侧向的平动位移模态，θx，θy和θz分别为机体滚转、俯仰和偏航模态。LA为旋翼摆振前进型，LR为旋翼摆振后退型。

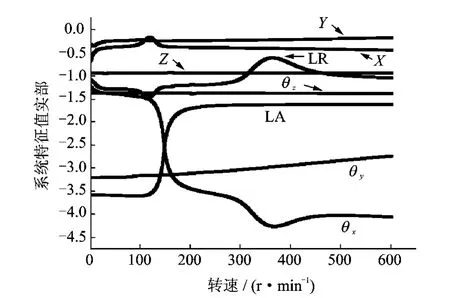
图23 原准机特征值实部Fig．23 Real parts of eigenvalues of original model

降低原准机摆振阻尼，在120r／min附近会出现不稳定区，如图24所示。

图24 降低原准机摆振阻尼后的特征值实部Fig．24 Real parts of eigenvalues after reducing damping of original model

由图24可以看出，系统在120r／min附近以及300～450r／min内发生不稳定。旋翼摆振后退型与机体平动自由度耦合，发生动力学不稳定。由于直八直升机额定转速为212r／min，因此，在额定转速内选择120r／min进行瞬态响应分析。在不稳定区线性模型与非线性模型受扰后的瞬态响应对比分析结果由图25～29给出。

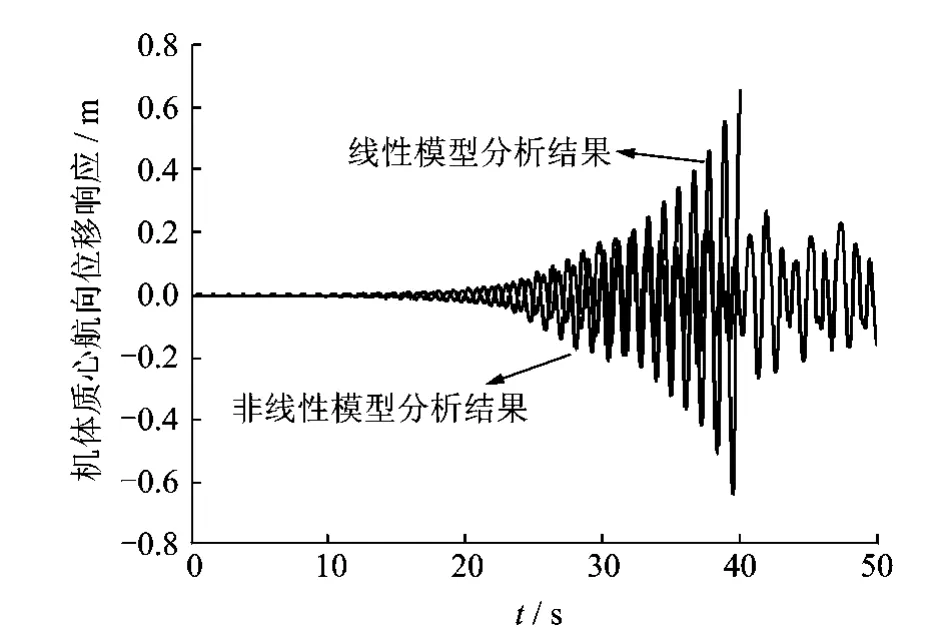
图25 机体质心航向位移响应Fig．25 Directional displacement response of fuselage centre of gravity

图26 机体质心横向位移响应Fig．26 Lateral displacement response of fuselage centre of gravity

图27 机体滚转自由度响应Fig．27 Roll response of fuselage

图28 机体俯仰自由度响应Fig．28 Pitch response of fuselage

图29 桨叶摆振自由度响应Fig．29 Lag response of blade

实测试验数据表明，“地面共振”现象发生时，机体及旋翼桨叶的运动是大幅值的极限环振动，结构由于无法承受巨大载荷导致毁坏。由图25～29结果可知，线性模型各自由度的计算结果均振荡发散，短时间内各自由度响应达到较大幅值，以致远超合理范围，不能反映实际响应情况。非线性动力学模型分析结果初始阶段与线性动力学模型分析结果一致，随着振动发散，非线性动力学模型的分析结果不会无限发散，进入大幅极限环振荡，这符合真实直升机“地面共振”发生时的运动特点。在仿真分析方面非线性动力学分析模型相对于传统线性分析模型，能更加贴近真实。

3 结 论

通过建立直升机开车过程旋翼／机体／起落架耦合非线性气弹动力学模型，模拟分析直升机开车过程瞬态响应，并应用于直升机地面开车过程的工程仿真研究。所建立的考虑非定常入流及气动力的非线性动力学分析模型将起落架和减摆器的实测数据作为特性输入，用于模拟动力学部件的非线性；并将真实操纵规律作为输入，可以有效分析直升机开车过程中，旋翼转速变化所引起的惯性力及气动力变化的影响；能够合理地模拟由于旋翼气动力的增加所导致的机体重心提升及起落架伸长等现象；模型还具有分析旋翼起动过程桨叶挥舞、摆振及起落架结构发生意外时瞬态响应的能力。数值分析结果表明，相对传统线性模型，旋翼／机体／起落架耦合非线性气弹动力学模型可对直升机地面开车过程进行更加贴近真实的各种动态仿真，丰富了设计研究手段。

［1］ 航空航天工业部科学技术研究院．直升机动力学手册［M］．北京：航空工业出版社，1991：292—305．

［2］ 张晓谷．直升机动力学设计［M］．北京：航空工业出版社，1995：80—135．

［3］ Z Xiao－gu．Physical understanding of helicopter air and ground resonance［J］．J．Am．Helicopter Society，1986，31（4）：4—11．

［4］ 王波，李书，徐亚妮．不同粘弹减摆器连接的直升机地面共振分析［J］．振动工程学报，2007，20（2）：123—127．

Wang Bo，Li Shu，Xu Yani．Analysis of ground resonance for helicopters with different elastomeric lag damper connections［J］．Journal of Vibration Engineering，2007，20（2）：123—127．

［5］ 胡国才．减摆器非线性特性及其对直升机旋翼／机体耦合动稳定性影响研究［D］．北京：北京航空航天大学，2004．

Hu Guocai．Nonlinear characteristics of blade lag dampers and its effect on helicopter rotor／airframe coupled dynamic stability［D］．Beijing：Beijing University of Aeronautics and Astronautics，2004．

［6］ 洪嘉振．计算多体系统动力学［M］．北京：高等教育出版社，1999：37—73．

Hong Jiazhen．Computational Dynamics of Multibody Systems［M］．Beijing：Higher Education Press，1999：37—73．

［7］ 杨卫东，董凌华．变转速倾转旋翼机多体系统气弹响应分析［J］．哈尔滨工业大学学报，2006，38（2）：282—324．

Yang Weidong，Dong Linghua．Multi－body aeroelastic analysis of tiltrotor with varying rotor rotational speed［J］．Journal of Harbin Institute of Technology，2006，38（2）：282—324．

［8］ Jonson W．Helicopter Theory［M］．NewYork：Dover Publications，INC，1980：196—207．

［9］ Dale M Pitt，David A Petters．Theoretical prediction of dynamic－inflow derivatives［A］．Sixth European Rotorcraft and Powered Lift Aircraft Forum［C］．Bristol England，1980：21—34．

［10］Leishman J G，Nguyen K Q．State－space representation of unsteady airfoil behavior ［J］．AIAA JOURNAL，1990，28（5）：836—844．

［11］Leishman J G，Gilbert L Crouse．State－space model for unsteady airfoil behavior and dynamic stall［A］．AIAA／ASME／ASCE／AHS／ASC 30thStructural Dynamics and Materials Conference［C］．Mobil，Alabama，American，89－1319－CP．1989：1 372—1 383．