基于比较视角的我国股票市场波动ARCH效应研究

耿庆峰 黄志刚

(1.福州大学管理学院，福建福州 350108；2.闽江学院公共经济学与金融学系，福建福州 350108)

基于比较视角的我国股票市场波动ARCH效应研究

耿庆峰1，2黄志刚1

(1.福州大学管理学院，福建福州 350108；2.闽江学院公共经济学与金融学系，福建福州 350108)

我国同期的主板市场不存在ARCH效应，中小板市场存在弱势ARCH效应，创业板市场存在明显的ARCH效应；GARCH(1，2)模型能较好地刻画中小板指数，GARCH(1，1)模型能较好地刻画创业板指数；EGARCH(1，2)能较好地刻画中小板市场波动的非对称性，EGARCH(1，1)模型能较好地刻画创业板市场波动的非对称性；GARCH(1，2)-M模型不能有效刻画中小板指数，GARCH(1，1)-M也不能有效刻画创业板指数，表明中小板市场及创业板市场日收益序列对风险溢价的敏感性不强。

创业板市场；ARCH模型；GARCH模型；EGARCH模型

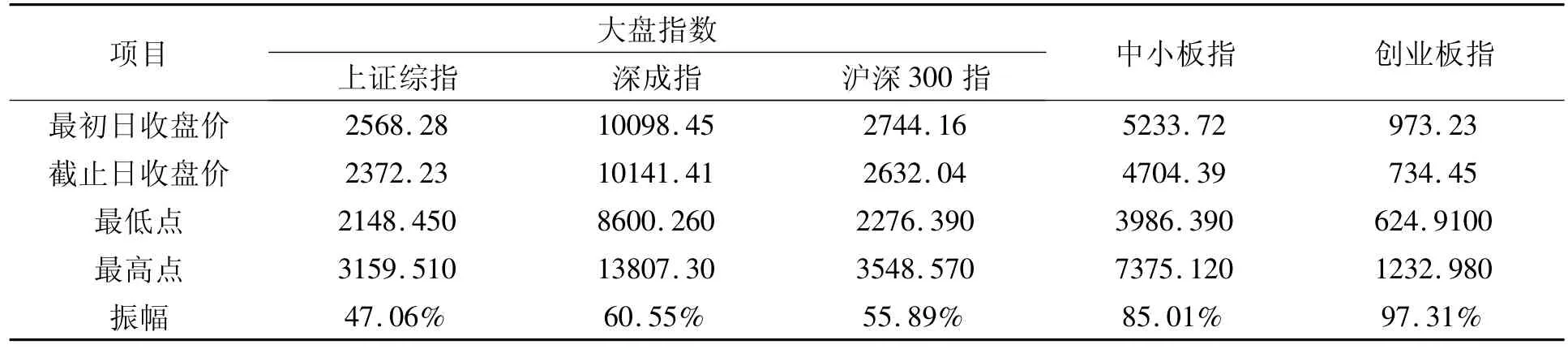
表1 两年时间股市市场指数变动情况

国内众多学者，以我国市场指数为研究对象，运用GARCH类模型对其收益率和波动率进行研究。大部分研究成果表明，我国证券市场存在ARCH效应，股价波动的集聚性、长记忆性、非对称性等特征明显，但波动溢价效应却并不明显。那么，作为独立于主板市场的新兴资本市场——创业板市场是否也具有波动ARCH效应?其与同期的主板市场、中小板市场波动表现存在何种差异?本文基于比较视角，利用自回归条件异方差(ARCH)类模型对我国主板市场及创业板市场的日收益率及其波动进行实证分析，以探究创业板市场与主板市场及中小板市场在微观机制上的不同。这一研究对于进一步完善创业板市场交易制度、提高政府监管可控性及为投资者提供投资建议都具有现实意义。

二、研究思路及方法

金融时间序列的一个显著特点是其波动随时间变化，ARCH模型能较好地刻画此特点。基于这一理论，本文探讨与创业板指数同期的五大市场指数波动特征。按照ARCH效应检验方法，对五大市场指数是否存在ARCH效应进行实证检验，对存在ARCH效应检验的创业板市场与中小板市场进行波动特征刻画，并对两市场波动的非对称性及波动溢价效应进行比较研究。

(一)GARCH(q，p)模型

GARCH模型是ARCH模型族中的一种带异方差的时间序列建模的方法。一般的GARCH(q，p)模型可以表示为：

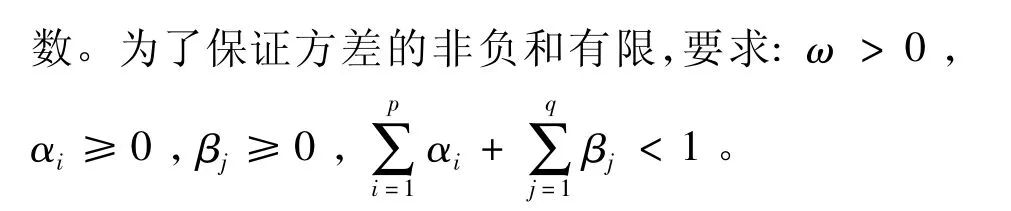
(二)非对称的ARCH模型

在资本市场中，经常可以发现这样的现象：资产的向下运动通常伴随着比之程度更强的向上运动。为了解释这一现象，Engle和NG绘制了好消息和坏消息的非对称信息曲线，认为资本市场中的冲击常常表现出一种非对称效应，描述这种非对称冲击的模型主要有：TARCH模型、EGARCH模型和PARCH 模型。［6］本文拟采用 EGARCH(Exponential GARCH)模型，其条件方差方程的定式为：

如果γ＜0，表明存在杠杆效应或反馈效应。

(三)GARCH-M模型

Bollerslev，Engle和Wooldridge发现美国股票市场的风险会影响股票市场的期望收益。［7］实际上，股票市场的投资者总是希望在一定的时间段内，对较高风险的投资，所获得的收益亦较高。这种利用条件方差表示预期风险的模型被称为ARCH均值或ARCH-M回归模型，是由Engle、Lilien and Robins引入的，其均值方程及方差方程表示为［8］：

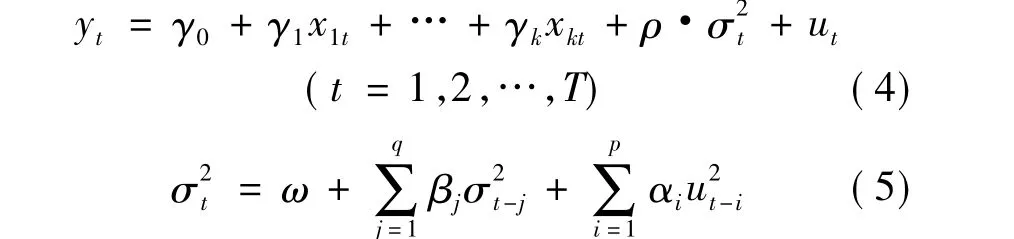
三、实证分析

(一)样本选取及数据处理说明

为了研究创业板市场与主板市场的异同，我们选取具有代表性的两大主板市场：上证综指和深成指。沪深300指数是由上海和深圳证券市场中选取规模大、流动性好的300只A股作为样本，在某种程度上，沪深300指数也代表了大盘指数，因此它也是主板市场的一重要组成部分。在我国创业板历史发展进程中，中小板市场是创业板市场发展的过渡产物，将创业板市场与中小板市场放在一起研究，具有重要的现实意义。创业板指数以2010年6月1日为基准日，基点为1000点，参照深证成份指数和深证100指数的编制方法和国际惯例编制而成，它反映了创业板市场的涨跌情况。以上五大指数样本区间均为2010年6月1日至2012年5月31日，以每天的收盘价为准，以St表示，共计484个观察值，数据来源于WIND金融数据库，所使用的软件为Eviews6.0。

日收益率公式写为：

其中，Rt为创业板指数日收益率，St为第t日的创业板指数收盘价，St-1为第t-1日的创业板指数收盘价。文中用 SHR、SCZR、HS300R、ZXBR 及CYBR分别表示上证综指收益率、深成指收益率、沪深300指数收益率、中小板指收益率及创业板市场指数收益率，利用以上公式，求得五大市场指数日收益率序列线状，见图1：

图1 五大市场指数收益率序列折线

从图1可以看出，创业板市场与中小板市场收益率序列存在三个特性：波动的持续性，即大的波动过后，要很长的时期能实现自身的修复；波动的集聚性，大的波动周围聚集着小的波动；波动的非对称性，向上的波动和向下的波动存在着不对称性。而上证综指、深成指及沪深300指数波动特征不明显。

(二)样本数据的特征分析

1.样本数据的正态性检验

本文运用Eviews6.0软件对创业板指数日收益率样本数据进行正态分布检验(也称J-B检验)，检验序列是否服从正态分布，J-B统计量是自由度为2的χ2分布，J-B统计量判断的标准是1%显著性水平下的临界值9.21，J-B统计量下显示的概率值P是J-B统计量超出原假设下的观测值概率。如果该概率值很小，则拒绝原假设，从而判断序列不服从正态分布。检验结果如表2所示。

从表2可知，五大指数收益率序列呈现出“尖峰厚尾”分布特征，表明五大指数收益率序列均不服从正态分布。

此外，表2中的数据还显示出：五大指数收益率序列的偏度值均为负的，图像具有长的左尾，具有不对称性且左偏，表示在五大指数的样本期间内日收益率小于平均值的交易日较多；序列的峰度值均大于正态分布的峰度3，相对于标准正太分布是存在“尖峰”特征的；J-B检验的结果全都远大于标准正态分布的临界值9.21，说明存在“厚尾”的特征。J-B检验结果的概率值均接近于0，表明五大指数收益率序列拒绝正态分布的假设。

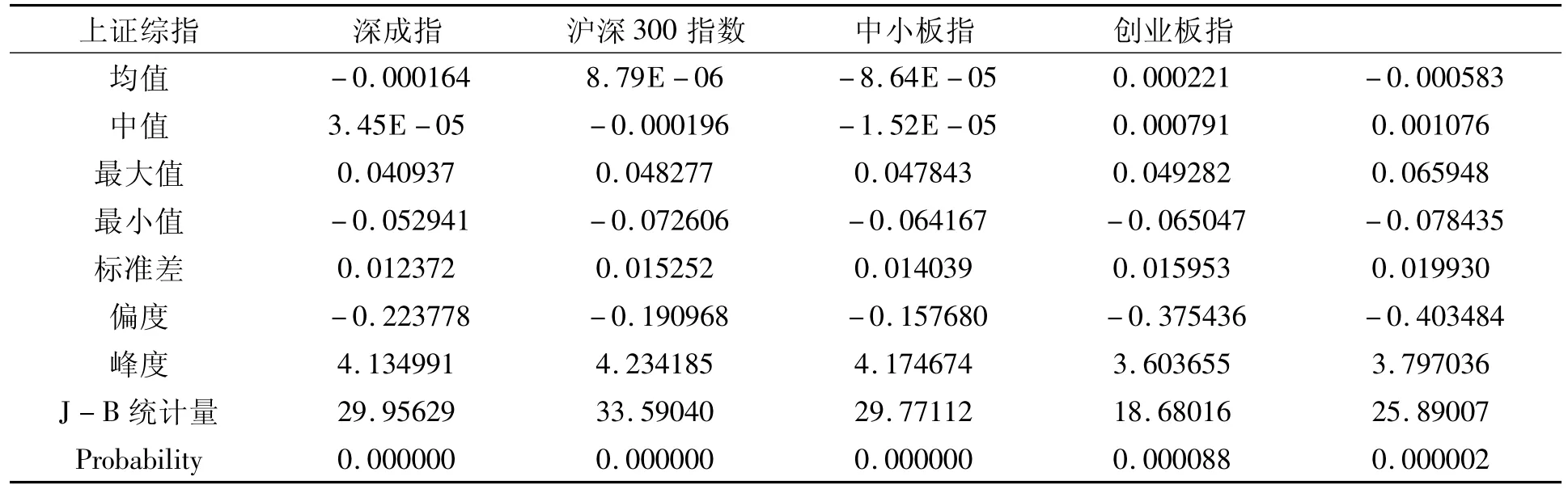
表2 创业板指数日收益率基本统计量

2.样本数据平稳性检验

在进行创业板指数日收益率时间序列分析之前，首先遇到数据的平稳性问题。GARCH模型对样本数据的要求是序列必须保持平稳。本文运用ADF(Augmented Dickey-Fuller test)方法检验方法进行平稳性检验，五大指数收益率序列ADF检验结果如表3所示。

ADF检验结果显示：P值趋于0，五大指数收益率序列在1%的显著性水平下拒绝原假设，接受不存在单位根的结论，因此可以判断五大指数对数收益率序列是平稳序列，说明利用ARCH类模型进行模拟是有效的。

表3 五大市场指数收益率序列ADF检验

3.样本数据相关性检验

通过Eviews6.0软件进行五大指数收益率序列进行检验，包括自相关函数(AC)和偏自相关函数(PAC)检验，AC函数可以用来根据该值等于0发生的时间j来选择MA(q)模型，j＞q；PAC函数可以用来根据该值等于0发生的时间j来选择AR(p)模型，j＞p。对创业板指数收益率检验结果如表4：

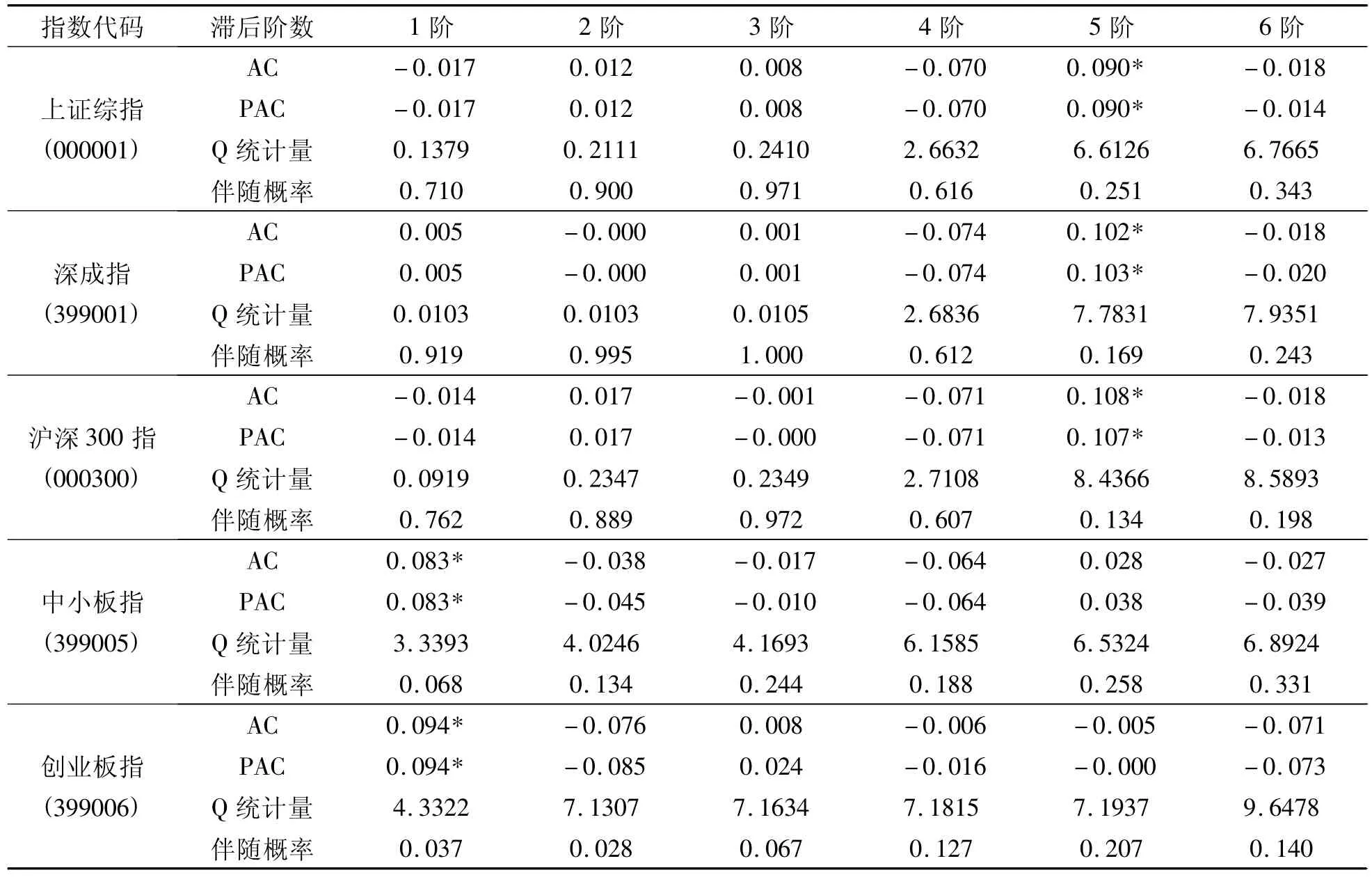
表4 五大指数收益率序列自相关检验

根据表4数据可知，上证综指、深成指、沪深300指数日收益率序列的5阶自相关函数、偏自相关函数值显著不为零，其余显著为零；中小板指数日收益率序列的1阶自相关函数、偏自相关函数在10%显著性水平下显著非零，创业板指数日收益率序列的1阶自相关函数、偏自相关函数在5%显著性水平下显著非零。说明五大指数收益率序列存在ARMA效应，根据AIC及SC准则，确定ARMA(5，5)来刻画上证综指、深成指及沪深300指数日收益率序列自相关性，ARMA(1，1)来刻画中小板指、创业板指数日收益率序列自相关性。

(三)ARCH效应检验

通常检验一个模型的残差是否含有ARCH效应的检测方法包括：ARCH-LM检验和残差平方相关图检验。本文运用ARCH-LM方法来检验主板市场及创业板市场指数收益率序列。检验结果如表5所示。

从表5可知，上证综指、深成指及沪深300指数收益率序列不存在ARCH效应，中小板指数收益率序列在10%的置信水平下存在ARCH效应，创业板指数收益率序列在5%的置信水平下，拒绝原假设，存在ARCH效应。

表5 五大指数ARCH效应检验结果

(四)中小板及创业板指数收益波动特征实证分析

1.方差方程估计

根据前文检验结果，中小板及创业板指数日收益序列存在明显的ARCH效应，本文试图建立收益率序列的GARCH(q，p)模型。建立GARCH模型之前，要先确定q和p的值。我们分别代入(1，1) 、(1，2) 、(1，3) 、(2，1)相关的数据组合，得出相应的AIC值，见表6：

表6 AIC测试结果

从上述测试中，可以得出GARCH(1，1)模型较好适合创业板指数收益率序列，GARCH(1，2)模型较好拟合中小板指数收益率序列，为了进一步确定该模型的适用性，在以上模型的基础上做残差序列ARCH效应检验，表7数据表明，统计量Obs*R-squared的值伴随概率为0.6634和0.7811，均大于显著性水平 0.05，接受原假设，认为残差序列已不存在ARCH效应，说明GARCH(1，1)及 GARCH(1，2)模型消除了残差序列的ARCH效应。

表7 残差序列ARCH效应检验

创业板指数日收益率方差方程中，GARCH项的系数在5%的统计水平下显著，ARCH项的系数在10%的统计水平下也是显著的，常数项不显著，尽管拟合优度不是太好，但AIC及SC值都较小，说明GARCH(1，1)模型基本能够拟合数据。

中小板指数收益率拟合方差方程中，GARCH项的系数在5%的统计水平下均显著，ARCH项在5%的统计水平下也是显著的，常数项也是显著的，尽管拟合优度不是太好，但AIC及SC值都较小，说明GARCH(1，1)模型基本能够拟合数据。

2.创业板指数收益波动的非对称性检验

在以系数估计中除α的估计值显著性不强外，其他各估计量在5%的显著性水平下具有明显的显著性，EGARCH(1，1)模型中非对称项γ的估计值为-0.1539。即，当ut-1＞0时，信息冲击对条件方差有一个负的0.1539倍的冲击；当ut-1＜0时，信息冲击对条件方差有一个正的0.1539的冲击。EGARCH(1，2)模型中非对称项 γ的估计值为-0.2195。即，当ut-1＞0时，信息冲击对条件方差有一个负的0.2195倍的冲击；当ut-1＜0时，信息冲击对条件方差有一个正的0.2195倍的冲击。

3.中小板指数及创业板指数收益波动的GARCH-M检验

本文通过GARCH(1，1)-M及GARCH(1，2)-M模型，对我国创业板市场和中小板市场进行实证研究，分析股票市场的风险对期望收益的影响。选取使用广泛的标准差影响模式，均值估计方程分别为：

在5%的显著性水平下，标准差系数估计均不显著。表明：中小板指数及创业板指数日收益波动对创业板收益影响不明显，即中小板和创业板均非“高风险、高收益”的投资场所。

四、结论与建议

通过对上证综指、深成指、沪深300指、中小板指及创业板五大指数的日收益率序列实证分析可以得到以下结论：

(1)中国股市上，不论是主板市场还是创业板市场，指数日收益率均不服从正态分布，呈现典型的“尖峰厚尾”特征，且五大指数日收益率序列均服从左偏分布。

(2)主板市场、中小板市场、创业板市场指数日收益率序列均存在显著的序列相关性，上证综指、深成指及沪深300指数日收益率序列存在5阶自相关和偏自相关，中小板指和创业板指日收益序列存在1阶自相关和偏自相关。

(3)包含上证综指、深成指及沪深300指数在内的主板市场均不存在ARCH效应，中小板市场存在弱势ARCH效应，创业板市场存在明显的ARCH效应。原因可能是由于选取时间窗口短，与经济周期密切相关的主板市场并没有走完一个完整周期。而中小板市场与创业板市场因规模小，受市场追捧及热炒，走势较好地走完了一个周期。另外，GARCH(1，1)模型能较好地刻画创业板指数日收益率序列，GARCH(1，2)模型能较好地刻画中小板指数日收益率序列。

(4)EGARCH(1，2)模型能较好地刻画中小板指数日收益率序列，两市场日收益率的波动均存在“杠杆效应”，即利空消息比同样大小的利好消息对市场波动性的影响更大。两市场的收益波动对收益影响均不明显，反映了两市场的日收益率序列对风险溢价的敏感性不强。从两市场波动率估计模型可知，中小板市场及创业板市场的波动性均具有较高的持续性，即当证券收益率一旦受到冲击出现异常波动，则在短期内很难得以消除。

(5)GARCH(1，1)-M 和 GARCH(1，2)-M模型估计参数不显著，表明“高风险、高收益”规律在中小板市场及创业板市场并不存在。这两个市场给投资者带来高风险的同时，并没有带来足够的高收益。

作为一种新型资本市场，创业板为中小企业融资提供了理想的平台，对中小企业的发展具有不可替代的作用。但同时也应看到，它还存在很多有待完善的地方，创业板市场股价波动实证验证了这一点。另外，作为管理层，对在创业板上市的企业审核应更加谨慎严格，让更多优质的、有核心竞争力的、真正具有成长性潜力的中小企业在创业板上市，这样既能促进中小企业的发展，同时也给偏好风险的投资者们提供一个好的投资机会。

注释：

［1］Eugene F.Fama，“The Behavior of Stock-Market Prices”，The Journal of Business，vol.38，no.1(1965)，pp.34-105.

［2］Engle，Robert F.，“Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K.Inflation”，Econometrica，vol.50，no.4(April，1982)，pp.987-1008.

［3］Bollerslev，Tim，“Generalized Autoregressive Conditional Heteroskedasticity”，JournalofEconometrics，vol.31，no.5(May，1986)，pp.307-328.

［4］［8］Engle，Robert，David M.Lilien and Russell P.Robins，“Estimating Time Varying Risk Premia in the Term Structure：The ARCH-Model”，Econometrica，vol.55，no.8(August，1987)，pp.391-406.

［5］Nelson，Daniel B.，“Conditional Heterosdasticity in Asset Returns：A New Approach”，Econometrica，vol.59，no.9(September，1991)，pp.347-370.

［6］Engle，Robert F.and Vivtor K.Ng，“Measuring and Testing the Impact of News on Volatility”，JournalofFinance，vol.48，no.8(August，1993)，pp.1022-1082.

［7］Bollerslev，T.，R.F.Engle and J.M.Wooldridge，“A capitalassetpricingmodelwith time-varying covariances”，Journal ofPoliticalEconomy，vol.96，no.3(March，1988)，pp.116-131.

［责任编辑：黄艳林］

F830

A

1002-3321(2013)02-0045-07

一、引 言

2009年10月23日，在中国证监会的批准下，我国创业板市场正式在深圳证券交易所开市，同年10月30日，首批28家公司上市，标志着“十年磨一剑”的创业板市场终于由理想变成现实。截止2012年5月31日，我国创业板恰值其2年零7个月，上市公司达319家，市场初具规模。两年来，创业板市场在各方的关注下不断成长、壮大，但也饱受争议，如“三高发行”、高管减持、业绩下滑等各种争议不断。从我国创业板指数来看，两年的时间，创业板指数由2010年6月1日的收盘价973.23点，到2012年5月31日的734.45点，指数呈一路下行状态，最高点1232.980点，最低点624.9100点，振幅高达97.31%，远高于同期上证综指的47.06%，深成指的60.55%，沪深300指数的55.89%，中小板指数的 85.01%(见表 1)。从海外创业板市场实践经验看，创业板市场初期表现出“交易频率低、流动性风险高、股价波动幅度大”等特点，且市场表现与主板市场有一定程度的脱节，是相对独立的高风险市场。

国外对股票市场价格的波动性研究已有很长一段历史。20世纪60年代，Fama就观测到资产的变化及收益率的变化具有稳定时期和易变时期，即价格波动呈现集群性，方差随时间变化而变化。［1］Engle提出的自回归条件异方差模型(ARCH)较好地模拟了随时间变化的方差模型。［2］Bollerslev在ARCH模型基础上提出了广义自回归条件异方差(GARCH)模型。［3］为了刻画时间序列受自身方差影响的特征，Engle，Lilien和Robins提出了 GARCH-M 模型。［4］Nelson 提出的EGARCH模型较好地描述了金融资产价格波动的非对称性。［5］

2012-10-26

福建省科技厅项目“福建创业投资引导基金运行机制的研究”(2012R0065)；福建省教育厅项目“海峡两岸中小企业融资模式研究”(JB12161S)；闽江学院“促进海西经济发展和提升自主创新能力的政策及技术研究”专项计划(YHZ10003)

耿庆峰，男，山东曲阜人，闽江学院经济系副教授，福州大学管理学院博士研究生；黄志刚，男，江西余干人，福州大学管理学院教授、博士生导师，博士。