一种EMD改进方法及其在旋转机械故障诊断中的应用

时培明，丁雪娟，李 庚，韩东颖

(1.燕山大学 电气工程学院，秦皇岛 066004;2.燕山大学 车辆与能源学院 ，秦皇岛 066004)

旋转机械故障诊断中，常常遇到诸如瞬变、调幅或调频等非平稳、非线性信号，提取和分析这些信号中的特征信息是机械诊断的关键。EMD是Huang首先提出的一种新型的时频分析方法［1］，能将复杂信号分解为有限个内禀模态函数(Intrinsic Mode Function，IMF)，适合处理非线性、非平稳信号。自EMD方法问世以来，它就引起了众多学者的广泛关注，已被应用于结构分析、设备诊断等领域［2-3］。

EMD方法的分析质量很大程度上取决于EMD分解的质量。而EMD分解由于采用三次样条插值来获取信号的瞬时平均，使得这种方法存在特殊的端点效应。另外，在Hilbert变换的过程中也存在端点效应，严重时会影响整个信号的分析结果。针对这一问题，研究人员已经提出了一些改进方法，如镜像延拓［4］、神经网络延拓［5］、相似极值延拓［6］、波形特征匹配延拓［7］、支持矢量回归机［8］等。但是，这些延拓法存在一个共同的问题，就是在延拓后，信号的端点仍然不确定，这样随着分解过程的进行，包络线两端仍可能存在发散现象，并逐渐向内“污染”，导致其端点效应问题依然存在。

本文提出一种波形特征匹配延拓和余弦窗函数结合的EMD端点效应处理方法。该方法在保留了波形匹配延拓方法优势的基础上，通过窗函数处理，使延拓部分逐渐减小直到归零，从而使延拓误差减小［9-10］。通过仿真分析和不对中故障诊断实例，验证了该方法的有效性。

1 改进的EMD时频分析方法

1.1 EMD分解方法

EMD时频分析方法适于处理非线性、非平稳信号。该方法包括两个过程:经验模态分解(EMD)和Hilbert变换。

EMD方法的分解步骤为:

(1)确定信号所有的局部极值点。

(2)利用三次样条线将所有的局部极大值点连接起来形成上包络线;将所有的局部极小值点连接起来形成下包络线。上、下包络线应该包络所有的数据点。

(3)上、下包络线的平均值记为m1(t)。

上述分解过程如图1所示，图(a)为原始信号，图(b)中·表示极大值点，◦为极小值点。图(c)中a为上包络线，b为下包络线，c为上、下包络线的均值。

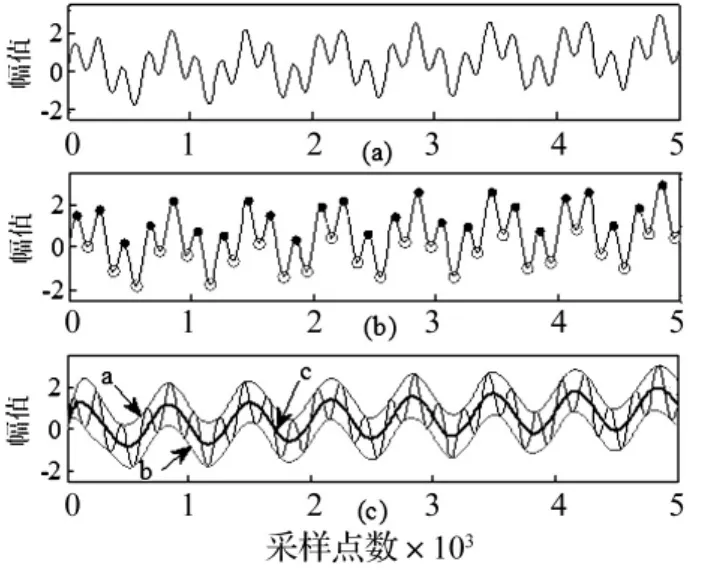
图1 EMD分解示意图Fig.1 Diagram of the EMD decomposition

(4)信号x(t)和m1(t)的差值为第一个分量，h1(t)为:

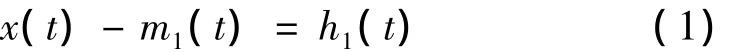
如果h1(t)是一个IMF，那么h1(t)就是第一个 IMF分量。

(5)如果h1(t)不满足IMF条件，把h1(t)作为原始数据，重复上述步骤，得到:

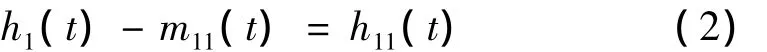
式中，m11(t)是h1(t)上下包络的平均值。反复筛选k次后，使得h1k(t)为IMF分量，即:

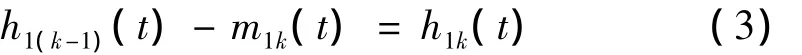
令:

从原始信号中获得的第一个IMF分量c1(t)应该包含信号最好的范围或者最短的周期成分。

(6)从x(t)分离出c1(t)，我们得到:

将r1(t)看作原始数据重复以上步骤，得到x(t)的第2个IMF分量c2(t)。重复循环n次，得到信号x(t)的n个IMF分量。这样就有:

当rn(t)成为一个单调函数不能再从中提取出满足IMF条件的分量时，循环结束。这样由式(5)和式(6)得到:

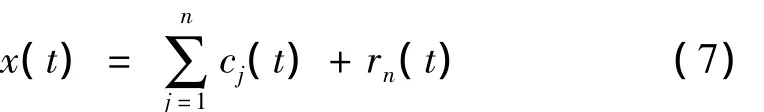
因此可以将信号分解为n个经验模态，残余函数rn(t)代表信号的平均趋势。从而对每一个IMF进行Hilbert变换，得到Hilbert谱及其边际谱。

对式(7)中的每一个内禀模态函数ci(t)作Hilbert变换得到:

构造解析信号:

于是得到幅值函数:

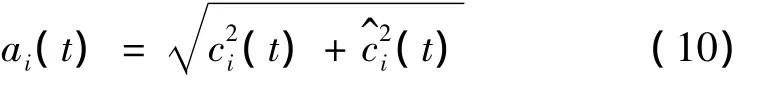
和相位函数:

进一步可以求出瞬时频率:

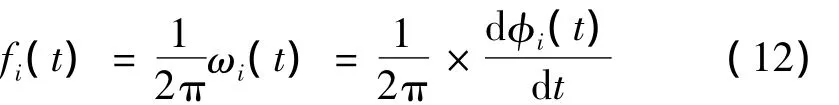
这样，可以得到:

这里省略了残余分量rn，RP表示取实部。展开式(13)称为Hilbert谱，记作:

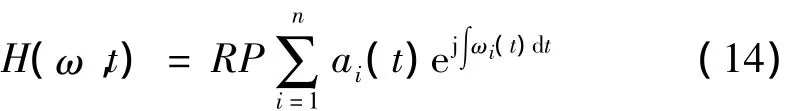
再定义Hilbert边际谱:

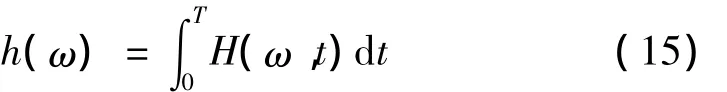
式中，T为信号的总长度。

1.2 EMD分解中的端点效应

EMD分解中由于无法保证端点处的极值点，导致求包络平均过程中，会在样条插值时产生数据的拟合误差。并且随着分解的进行，误差不停积累，由端点处向内逐渐传播，严重时会使分解的数据失去意义。

图2为仿真信号x(t)的EMD分解结果，信号x(t)由两个正弦信号和一个调幅信号组成，其表达式为

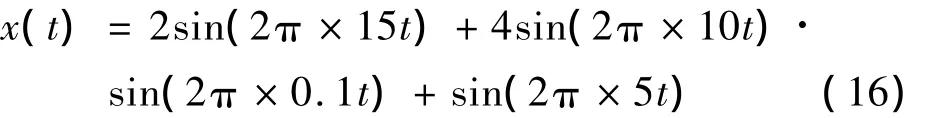
分解时没有对原始数据进行任何处理。由图2所示，信号x(t)分解出来的3阶IMF都有严重的端点效应。

图2 未经过处理的EMD分解结果Fig.2 The decomposition result of simulative signal without being processed

1.3 基于波形特征匹配延拓与余弦窗函数的EMD方法改进

基于波形特征匹配的数据延拓方法是通过采用信号内部和边缘处变化趋势最为相似的子波来对端点处数据进行延拓，它是一种自适应的方法。在具体实现中，通过计算波形匹配来量化两端波形的变化趋势。

如图3所示，以左边界第一个极值点为极大值为例，Mi、Ni(n=1，2，3，…)分别为曲线的极大值、极小值点，分别对应时间tmi、tni，S1为左端点，波形特征匹配延拓法以S1-M1-N1为边界特征波形，在全部数据中找到与S1-M1-N1构成的三角形最接近的波形为匹配波形，如Si-Mi-Ni，从Si的前一点(右边界为后一点)数据开始，向前(右边界向后)延拓波形数据，使延拓数据符合信号的自然走向。

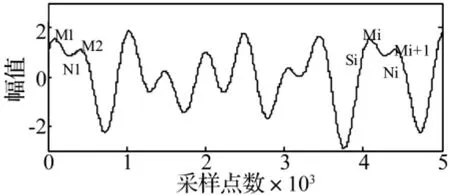
图3 波形特征匹配原理图Fig.3 Diagram of wave characteristic matching

具体步骤为:

(1)根据S1-M1-N1边界三角形的时间坐标，寻找与S1对应的点Si，其对应的时间由式(17)求得:

图4 信号x(t)的波形匹配延拓结果Fig.4 Results of wave characteristic matching

由于得到的tsi不一定在采样点上，采用线性插值求其精确值Si。

(2)计算匹配误差Ei

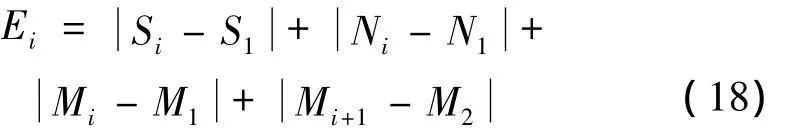
式中，最后一项为匹配波形的趋势项，反映特征波形在曲线中相对极值点的位置。

(3)取Ei最小的波形为匹配波形，若存在多个相等的Ei，为获得足够的延拓数据供选择，取与起始点距离最远的波形为匹配波。

(4)自匹配波形与Si距离最近的数据点的前一点开始，将实际波形数据延拓到S1前，延拓点数据根据需要选择，若信号中Si前数据点个数小于需要延拓的点数，可反复延拓此段波形。

(5)采用同样的原理可以对右边界数据进行延拓。

(6)采用延拓后的数据完成EMD分解。信号包络插值计算采用延拓后的全部数据，而在EMD分解结束条件的计算中，仍采用有效数据。

(7)对EMD分解得到的IMF作Hilbert变换，此时数据长度为延拓后数据总长，按原始信号长度及位置取分析结果，得到有效数据的EMD分析结果。

在上述延拓过程中兼顾了数据的极值点及非极值点的波形数据，使得延拓数据与原信号交界处光滑过渡，避免了边界处瞬时频率的跳跃。

图4是信号x(t)基于波形匹配延拓的结果。由图可以看出延拓部分虽然与实际信号比较接近，但还是存在误差。对延拓数据加余弦窗函数处理，控制端点效应向内“污染”，得到更准确的IMF。

定义余弦窗函数:

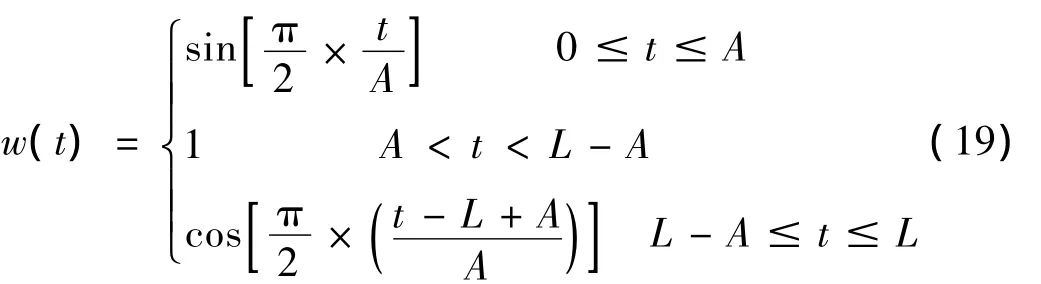
式中，L为信号延拓后的长度，A为信号两端延拓中较长的延拓长度。

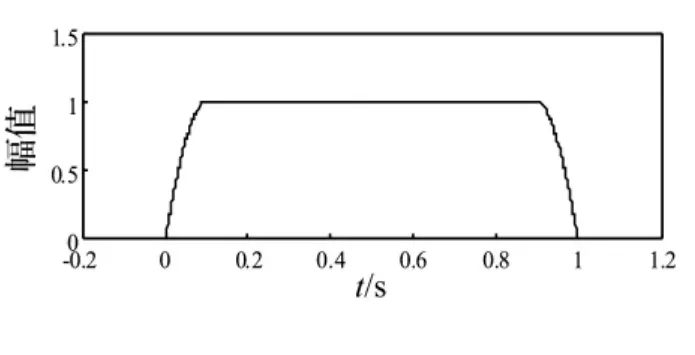
图5 余弦窗函数Fig.5 The shape of cosine window

图6 信号延拓加窗处理结果Fig.6 The results processed with the proposed method

余弦窗的形状如图5所示。

余弦函数窗将延拓误差“控制”在信号两端，使其无法(或以较慢速度)向数据内部发展，保证信号中部数据的正确分解。首先，将延拓信号x(t)与余弦窗函数进行内积运算，得到信号y(t)=〈x(t)，ω(t)〉。

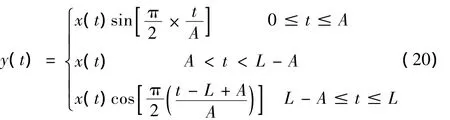
然后，对处理后的信号y(t)进行EMD分解，再将分解得出的IMF的两端去掉相应的延拓部分A。最后对减去延拓部分后的IMF进行边界谱分析。该方法既考虑到了延拓误差又考虑到了信号的完整性。

图6为信号x(t)延拓后再加余弦窗处理的结果。从图中可以看出延拓的部分逐渐减小直到归零，从而使延拓部分误差减小，为得到更准确的IMF提供了可靠条件。

2 仿真分析

对经过处理的信号x(t)进行EMD分解得到3阶IMF，并与实际信号作比较如图7。通过与图2对比发现经过延拓加窗处理得到的IMF明显更符合实际值，说明该方法对抑制端点效应有良好的效果。

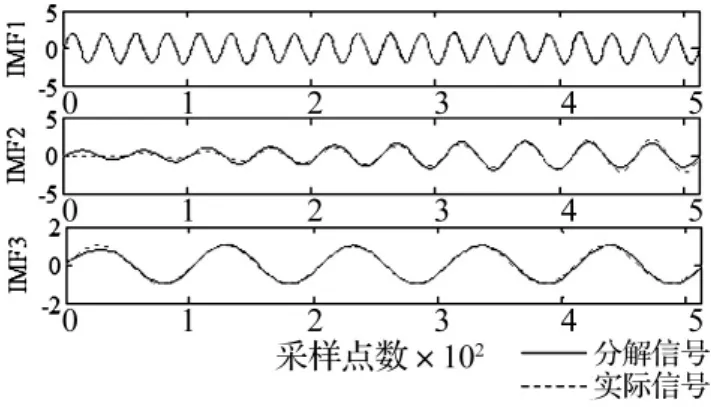
图7 延拓加窗后的分解结果Fig.7 The decomposition result of simulative signal with the proposed method

图8、图9分别是信号x(t)未经过处理和用改进方法得到的Hilbert谱与边界谱。由图8可以看出，未处理的Hilbert谱在信号两端有比较严重的发散现象，而通过本文方法处理后的Hilbert谱效果有明显的改善。图9中(a)的幅值显示明显有很多微弱振荡，尤其是在高频部分尤为明显。通过端点效应处理后得到的边界谱(b)中，幅值振荡基本消除，得到了更好的处理效果。

3 EMD改进方法在不对中故障诊断中的应用研究

图8 Hilbert时频谱对比图Fig.8 The composition of Hilbert spectrum

图9 边际谱对比图Fig.9 The composition of marginal spectrum

将本文提出的EMD改进方法应用于转子不对中故障信号的特征提取及诊断。图10是采集信号的时域波形，转速为900 r/min，采样频率为768 Hz。图11是故障信号的EMD分解结果，图12、图13分别是改进前后信号的Hilbert谱及边际谱。

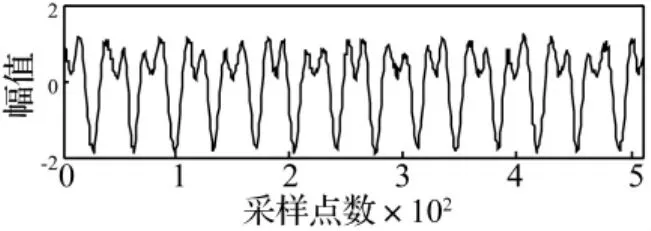
图10 不对中故障的时域波形Fig.10 Time domain waveform of misalignment fault

图11 故障信号的EMD分解结果Fig.11 The decomposition result of fault signal

图11中的内禀模态函数IMF1，IMF2，IMF3被依次分解出来，分别对应着多倍频、2倍频和基频振动模态，但是因为噪声的存在，一定程度地影响了EMD的分解精度［11-12］。由Hilbert时频谱图可观察到，基频分量和2倍频左右的分量在分析的时间内一直稳定存在，除此之外还有多倍频分量，但并不稳定;比较图12，改进后的Hilbert谱的端点发散现象得到了明显的改善，尤其是信号的左端更为明显。在Hilbert边际谱的频幅谱中观察到，除了基频还有其他倍频信息存在，基频分量和2倍频分量占主导地位，且2倍频分量强度并未超过基频分量;比较图13，改进后的边际谱幅值微弱振荡基本消除，且2倍频分量得到了突出。根据以上分析诊断该转子的故障为不对中故障。

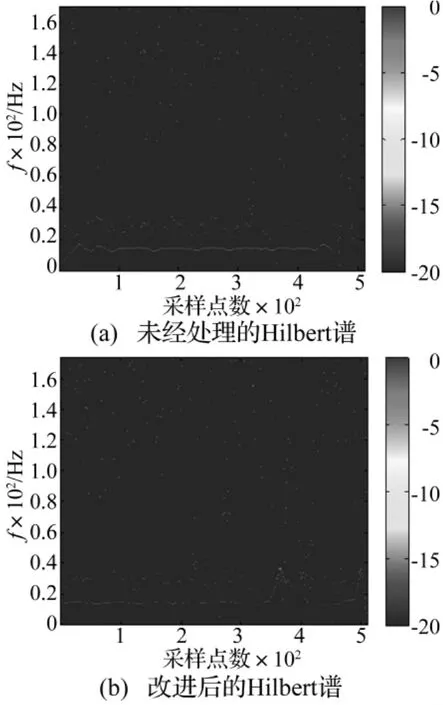
图12 故障信号的Hilbert谱Fig.12 The Hilbert spectrum of fault signal

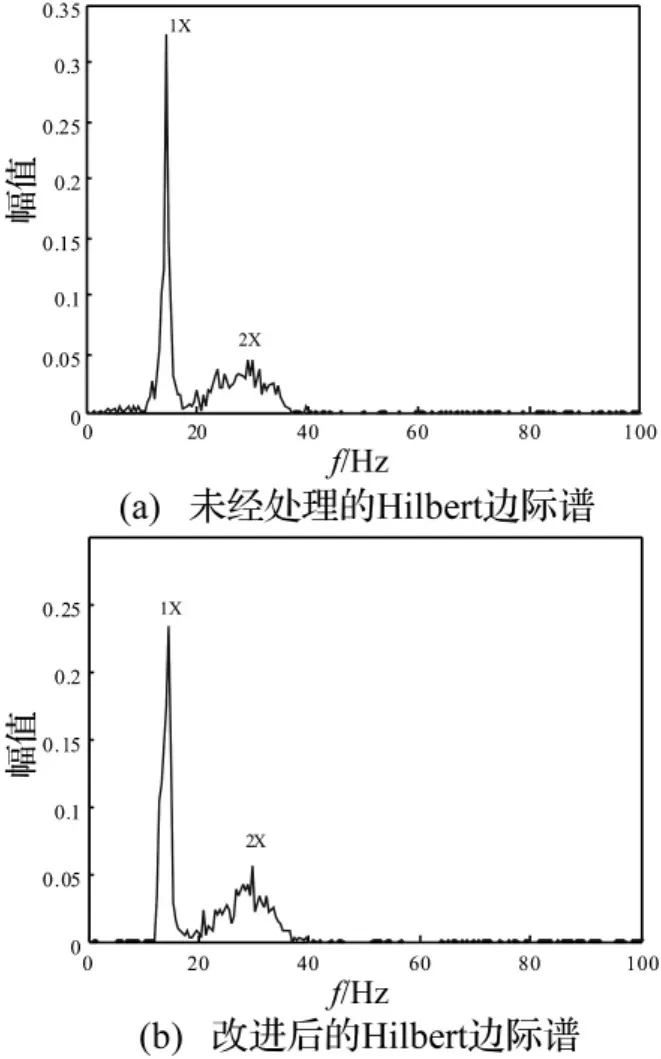
图13 故障信号的Hilbert边际谱Fig.13 The marginal spectrum of fault signal

4 结论

(1)提出了一种抑制端点效应的新方法，首先利用波形特征匹配延拓对信号两端进行延拓，然后根据延拓情况对信号加余弦窗进行处理，把延拓误差控制在两边。最后在EMD分解后，只取信号的有效长度，提高了分解的精度。

(2)通过仿真信号的分析，证明了该方法能有效地抑制端点效应，为得到准确地边际谱和Hilbert谱提供了保障。

(3)将改进方法应用到旋转机械故障诊断中，通过对含有不对中故障的信号进行分析，证明了该方法能从非线性故障信号中得到真实有用的故障信息，实现旋转机械故障的有效诊断。

［1］Huang N E.The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis［J］. Proc. R. Soc. Lond. A，1998，454:903-995.

［2］ Cheng J S，Yu D J，Tang J S，et al.Local rub-impact fault dianosis of the rotor systems based on EMD［J］.Mechanism and Machine Theory，2009，44:784-791.

［3］Yang B，Suh C S.Interpretation of crack-induced rotor nonlinear response using instantaneous frequency［J］.Mechanical System and Signal Processing，2004，18(3):491-513.

［4］韩建平，钱 炯，董小军.采用镜像延拓和RBF神经网络处理EMD中端点效应［J］.振动、测试与诊断，2010，30(4):414-417.

HAN Jian-ping，QIAN Jiong，DONG Xiao-jun.Suppression of end-effect in empirical mode decomposition by mirror extension and radial basis function neural network prediction［J］.Journal of Vibration，Measurement＆Diagnosis，2010，30(4):414-417.

［5］胡劲松，杨世锡.EMD方法基于径向基神经网络预测的数据延拓与应用［J］.机械强度，2007，19(6):894-899.

HU Jin-song，YANG Shi-xi.Application of EMD method with data extension technique based on RBF neural network to time-frequency analysis［J］.Journal of Mechanical Strength，2007，19(6):894-899.

［6］沈 路，周晓军，张志刚，等.Hilbert-Huang变换中的一种端点延拓方法［J］.振动与冲击，2009，28(8):168-174.

SHEN Lu， ZHOU Xiao-jun， ZHANG Zhi-gang， et al.Boundary-extension method in Hilbert-Huang transform［J］.Journal of Vibration and Shock，2009，28(8):168-174.

［7］胡爱军，安连锁，唐贵基.HILBERT-HUANG变换端点效应处理新方法［J］.机械工程学报，2008，44(4):154-158.

HU Ai-jun， AN Lian-suo， TANG Gui-ji. New process method for end effects of Hilbert-Huang transform［J］.Journal of Mechanical Engineering，2008，44(4):154-158.

［8］程军圣，于德介，杨 宇.基于支持矢量回归机的Hilbert-Huang变换端点效应问题的处理方法［J］.机械工程学报，2006，42(4):23-31.

CHENG Jun-sheng，YU De-jie，YANG Yu.Process method for end effects of Hilbert-Huang transform based on support vector regression machines［J］.JournalofMechanical Engineering，2006，42(4):23-31.

［9］Qi K Y，He Z J，Zi Y Y.Cosine window-based boundary processing method for EMD and its application in rubbing faultdiagnosis［J］. MechanicalSystems and Signal Processing，2007，21:2750-2760.

［10］于慧君，陈章位，王庆丰.一种加窗重叠信号平滑连接方法及其在振动信号预处理中的应用［J］.振动与冲击，2007，26(8):39-40.

YU Hui-jun，CHEN Zhang-wei，WANG Qing-feng.OLA signal smooth linking method and its application in vibration signal pre-processing［J］.Journal of Vibration and Shock，2007，26(8):39-40.

［11］ Jalan A K，Mohanty A R.Model based fault diagnosis of a rotor-bearing system for misalignment and unbalance under steady-state condition［J］.Journal of Sound and Vibration，2009，327(3-5):604-622.

［12］ Rybczyński J.The possibility of evaluating turbo-set bearing misalignment defects on the basis of bearing trajectory features［J］.Mechanical Systems and Signal Processing，2011，25(2):521-536.