基于动应变的桥梁动态称重及其优化算法
王宁波,任伟新,万华平
(中南大学 土木工程学院,长沙 410075)
车辆荷载作为在役桥梁最重要的活荷载之一,在桥梁的各种荷载组合中占有重要地位。监测桥上移动车辆荷载,明确其分布特点对在役桥梁承载能力评估、桥梁剩余寿命预测、桥梁结构可靠度设计以及运营维护管理等方面都具有重要意义。
对桥梁移动车辆荷载的测定,目前国内采用较多的方法是路面式动态称重,它通过在进桥路面段行车道路面埋入(压电式)或顶部安放(弯板式)传感器系统来检测车辆轴重、轴距等信息。路面式动态称重的优点是能适合任意桥梁结构并可长时间采集数据,其主要缺点是只能测定车轮压在传感器上几毫秒短暂时间段内的动压力,由于不能记录动荷载完整的周期振动,通常情况下该压力值与静态轴重存在偏差[1],此外,路面式动态称重的识别精度受传感器宽度、车辆行驶速度以及路面平整度的影响很大。
基于动应变的桥梁动态称重是另外一种车辆荷载测定方法,通过在桥梁不同截面底部安装应变计测定车辆过桥时间段内动应变响应,以此来识别车速、轴距,以及轴重、车重等信息。相较路面式动态称重而言,基于动应变的桥梁动态称重对车辆荷载信息测试记录时间长,能获取的数据量大,还具有系统安装维护简便,不中断交通、对路面无破坏、耐久性好等优点。Moses等[2]首次提出了根据桥梁动应变进行车辆动态称重的一般原理,Peters[3]将这一应用延伸至涵洞结构,并引入“峰值法”来进行荷载识别。20世纪末,欧盟委员会应10个参与国相关组织机构的提议启动WAVE project,针对路面车辆荷载及轴重测定展开一系列理论与试验研究[4],至此基于动应变的桥梁动态称重开始受到关注。Rowley等[5]在荷载识别中采用正则化优化算法,与初始最小二乘法的结果比较并得出结论:采用精确的桥梁影响线结合正则化技术将大幅提高动态称重精度。Chatterjee[6]将小波变换用于应变信号处理以提取精确的车轴信息。Michael[7]针对车辆行驶在桥面不同横向位置时产生明显不同动应变的现象,研究了二维桥梁移动荷载识别问题,并初步考虑多个车辆连续从桥上通过的工况。O’Brien等[8]根据实测桥梁应变数据对影响线进行反算,从而实现了对桥梁影响线测定。基于动应变的桥梁动态称重因为其数据信息量丰富、安装维护简便、耐久性能好等优点在欧、美、日、等国家逐渐受到青睐,一些国家开始以此来取代传统路面式动态称重系统[9-10]。
基于动应变的桥梁动态称重研究多采用理论仿真分析与现场试验研究相结合的手段。本文结合车-桥耦合振动模型进行仿真分析,详细阐述了根据动应变进行桥梁动态称重(包括车辆行驶速度、轴距、轴数的识别以及车辆、车轴称重)的基本理论,并针对已具备一定精度的桥梁动态称重初始结果值,采用梯度法进行多参数局部优化研究,进一步提高结果精度,体现了基于动应变的桥梁动态称重算法的可行性。
1 基于动应变的桥梁动态称重基本理论
根据车辆从桥上行驶所产生的桥梁动应变来提取车辆荷载,是典型的“第二类反问题”。车辆过桥时桥梁动应变信号按其产生原因主要可分成车辆荷载引起的桥梁振动部分、桥梁自由振动部分和噪声部分,若忽略桥梁惯性力(即桥梁自由振动部分),移动车载部分产生的桥梁动应变可近似等同于相应影响线与荷载值的乘积。根据这一特性采用桥梁影响线模拟实测动应变信号,得到应变理论值,比较实测值与理论值,并结合最小二乘法求解车辆各轴重,即实现动态称重。
1.1 桥梁影响线确定
桥梁影响线描述桥梁在移动单位荷载作用下的静态特性,桥梁影响线精度是贯穿动态称重的重要指标。理论上可通过桥梁的尺寸、材料、支撑等参数计算获取不同断面桥梁影响线,实际情况下由于支撑条件不确定性(多介于理想简支与完全固支之间)、材料老化、弹性铺装等因素使得该方法的计算结果并不理想,通常需在上述基础上通过调整支座约束条件对影响线作适当修正。此外,还可以通过利用标准车辆过桥的实测数据直接计算得到桥梁影响线[8]。
1.2 桥梁动态称重基本理论
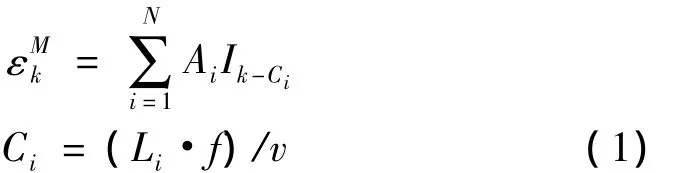
其中:N为车辆轴数;Ai为第i轴轴重;Ik-Ci为测点k对应第I车轴影响线纵坐标值,根据桥梁影响线获得;Li为第i轴与第1轴之间的距离(L1=0);f为数据采样频率;v为车辆行驶速度;Ci为与轴距Li相对应的采样点数。
定义误差函数:

联立式(1),式(2),根据最小二乘原理:
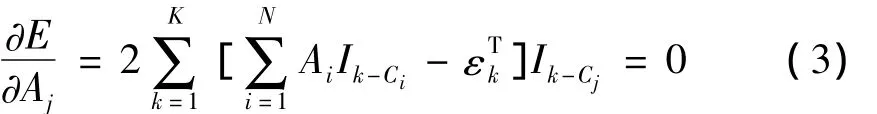
K指采样点总数;j=1,…,n,表示车轴数。对式(3)化简得:

j有N个取值,对应N个等式,令:
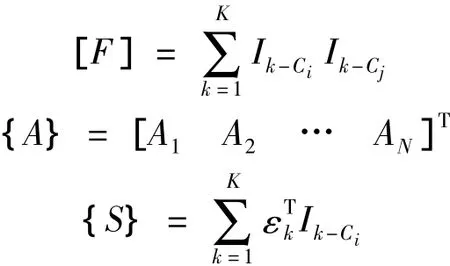
则有:
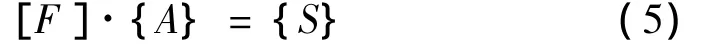
求解方程(5)即得到车辆轴重列阵Aj。从以上推导过程不难发现,采用该方法计算得到的车辆轴重值精度受车辆行驶速度、轴距等参数精度的影响很大。
2 初始识别结果值局部优化
基于动应变的桥梁动态称重算法,需以准确的车辆行驶速度、轴距、等信息为基础,当前者识别结果存在误差时将直接导致轴重识别偏差。针对这一问题,对上述桥梁动态称重算法得到的初始结果值进行局部优化,以降低速度、轴距等参数识别误差对轴重的影响,进一步提高精度。
本文选用梯度法作为局部优化算法,对车辆速度、轴距及轴重等识别值进行多参数局部优化,具体优化过程定义如下:
目标函数,最小值:
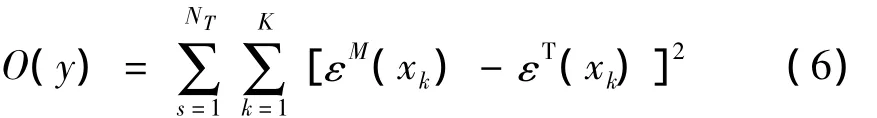
其中:K是总采样数点,k表示第k采样点;xk与k相对应,表示第1轴与指定参考点之间的距离;NT表示采用的测点总数。
优化参数:
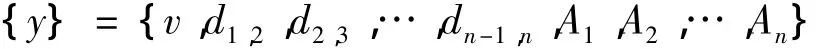
其中:dn-1,n表示第n-1 轴与n轴之间距离,即:dn-1,n=Ln-Ln-1。v,Ai含义与前文相同。
初始值:
选定桥梁动态称重初始结果值作为优化算法初始输入值。
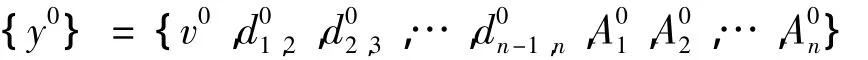
约束条件:
为保证目标函数O(y)最小值的唯一性,即Hessian矩阵特征值均为非负,需对参数取值范围进行约束,针对优化参数,v,d1,2,d2,3,…,dn-1,n,A1,A2,…,An的具体约束条件为:
(1)速度v取值范围与初始值v0偏差±5%,这要求速度的初始识别精度±5%在范围内[7]。
(2)当识别的初始值足够精确时,无需对轴距值进行约束,本文设定上下限值范围与初始值偏差±20%。
(3)轴重总和(即车辆总重量)与速度v之间关系如文献[11]。
(4)所有参数取值均为正。约束条件表达式如下:

式中:λ=k∫ε(t),k是与测点对应的桥梁影响线相关的常数。
结合matlab7.0优化工具箱fmincon函数对桥梁动态称重初始结果值进行优化研究,通过迭代计算求解该有约束优化问题的极小值,从而实现对车辆行驶速度、轴距、轴重等参数的局部优化,进一步提高其精度。基于动应变的桥梁动态称重及其优化算法基本流程如图1。
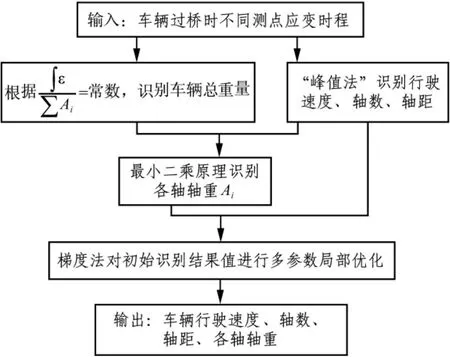
图1 桥梁动态称重与优化算法流程Fig.1 Flowchart for bridge WIM and optimization algorithm
3 算例分析
以三轴车辆行驶通过简支梁桥为例,建立汽车-桥梁耦合振动方程,并进行迭代求解模拟车辆以恒定速度过桥时桥上测点动应变响应,根据模拟的动应变响应曲线对本文基于动应变的桥梁动态称重算法进行数值仿真。
三轴车辆模型如图2所示,该模型对应移动荷载识别对象(或优化参数个数)共 6个,分别为v,d1,2,d2,3,A1,A2,A3。车辆模型相关参数源于文献[12],具体如下:

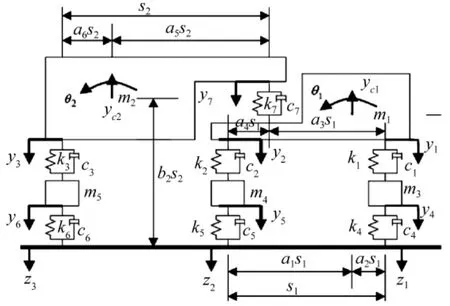
图2 三轴车辆模型Fig.2 Three-axle vehicle modal
桥梁模型参数:桥长Lb=16 m,抗弯刚度ET=4.36×109Nm2,阻尼系数ξ=0.02,线密度ρA=1.07 ×104kg/m,梁中心线距离底缘0.41 m,假定桥面平顺性好,平顺性等级设为A级。在桥梁1/8跨、1/4跨和3/4跨截面底缘处设定应变测试点,其中1/8跨测点主要用于车轴检测,1/4跨和3/4跨测点用于动态称重研究。
基于以上三轴车辆和桥梁模型,假定车辆在空载和装载10 t(车辆质心位置不改变)情况下,分别以20、36、54、60 km/h等速度过桥,共记6种工况,模拟计算桥梁1/8、1/4、3/4截面测点动应变响应。首先根据“峰值法”识别车速v、轴距d1,2和d2,3,结合应变曲线积分面积与车辆重量比值恒定的特性识别车辆总重量,采用桥梁应变影响线拟合实测动应变曲线,利用最小二乘法识别三轴重A1、A2、A3。将上述6个参数识别结果值作为局部优化初始值。优化目标函数定义时仅考虑桥梁1/4、3/4截面的两测点,即(6)式中NT=2,这与实际工况一般选定两个断面进行测试相一致。根据本文提出的多参数局部优化算法对移动荷载识别结果进行优化。相关计算及分析结果如表1和图3所示。
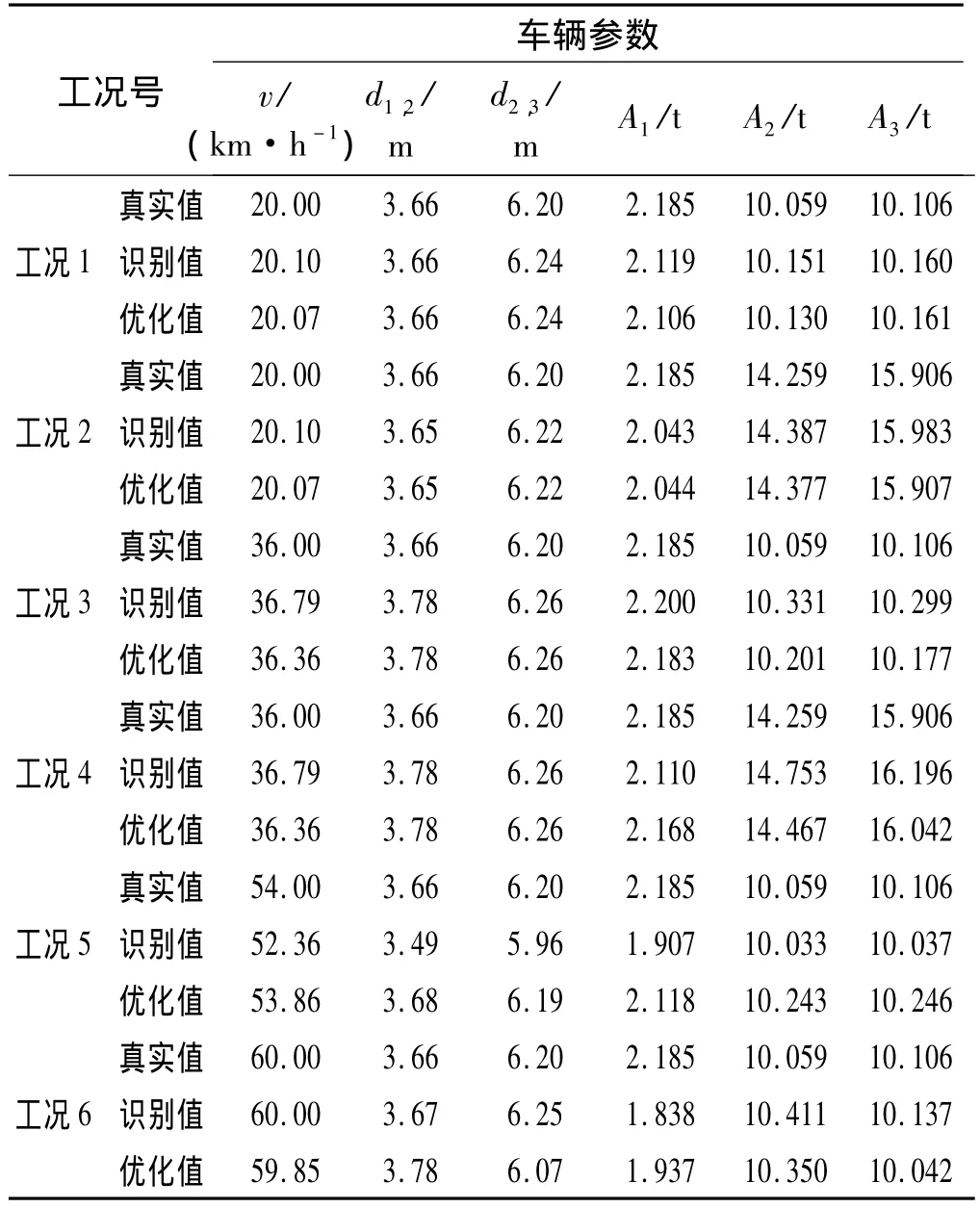
表1 车辆参数识别值及其优化值Tab.1 identification values and its optimization results for vehicle parameters
由表1和图3的数据比较分析可知,当行驶速度为20 km/h时,初始荷载识别值与优化结果值差异并不明显,这是因为初始值已具有很高精度;当行驶速度大于36km/h时,优化值较识别结果值更接近真实值,尤其针对车辆行驶速度、轴重等参数,这表明:对桥梁动态称重初始结果值进行局部优化能够提高精度。
该数值算例中引用的三轴车辆模型各轴重分布较不均匀,轻轴重量不及总重量1/10,对轻轴识别误差偏大,图3(f)最为明显,此外模型中车轮与路面单点接触形式过于简单,不能考虑车轮对路面不平顺的包容特性,这导致模拟的桥梁动应变响应曲线与实际情况存在偏差,上述因素的存在使得没能更好地体现本文桥梁动态称重及其优化算法在精度方面的优势。
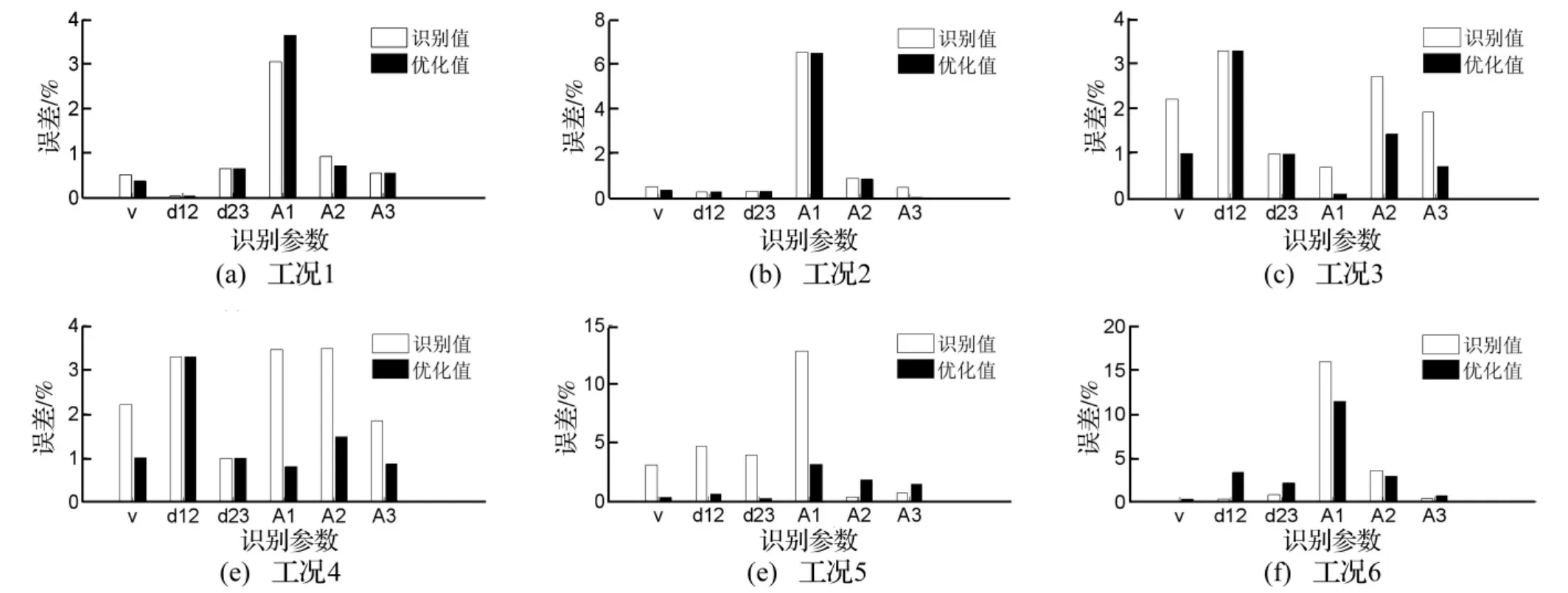
图3 识别值与优化值误差比较Fig.3 The error compare of identification values and optimization results
4 结论
根据桥梁动应变响应进行动态称重,采用梯度法对初始结果值进行多参数局部优化,以消除速度、轴距等识别偏差对整体结果的影响,达到提高车辆荷载识别精度的目的。结合车-桥耦合振动模拟桥梁动应变响应,对上述方法进行数值仿真分析,得到主要结论如下:
(1)基于动应变的桥梁动态称重对车载信息测试记录时间长,获取的数据信息量大,这是准确提取车辆荷载信息的前提条件。
(2)对已经具备一定精度的动态称重初始结果值进行局部优化,能进一步提高精度,满足工程应用要求。(3)采用梯度法进行多参数局部优化时,通过合理选定约束条件避免产生多个最小目标值,从而实现快速优化。
(4)桥梁影响线的准确性是影响桥梁动态称重的重要指标,对影响线的测定是有待进一步研究的问题。
[1] McNulty P,O'Brien E J.Testing of bridge weigh-in-motion system in sub-arctic climate[J].Journal of Testing and Evaluation,2003,31(6):1-10.
[2]Moses F.Weigh-in-motion system using instrumented bridges[J].Transportation Engineering Journal(ASCE),1979,105(3):233-249.
[3]Peters R J.An Unmanned and Undetectable Highway Speed Vehicle Weighing System[C]//ARRB Transport Research.Proceedings ofthe 13thARRB-5thREAAA Combined Conference(part 6).Australian:Australian Road Research Board,1986:70-83
[4]Jacob B.Action COST 323:Weigh-in-motion of road vehicles[C]//E J O’Brien,et al.Pre-Proceedings of Second European Conference on Weigh-in-motion of road vehicles.Lisbon:European Commission,1999.25-33.
[5]Rowley C,Gonzalez A,O’Brien E J,et al.Comparison of conventional and regularized bridge weigh-in-motion algorithms[C]//B Jacob,et al. Proceedings of the International Conference on Heavy Vehicles.Paris,France:John Wiley,2008.221-230.
[6] Chatterjee P,OBrien E J,Li Y Y,et al.Wavelet domain analysisforidentification ofvehicle axlesfrom bridge measurements[J].Computers and Structures,2006,84:1792-1801.
[7] Michael Q.Bridge weigh-in-motion development of a 2-D multi-vehicle algorithm [D].Sweden:Royal Institute of Technology,2003.
[8] OBrien E J,Quilligan M J,Karoumi R.Calculating an influence line from direct measurements[J].Proceedings of the Ice-Bridge Engineering,2006,159(1):31-34.
[9] Kobayashi Y,Miki C,Tanabe A.Long term monitoring of traffic loads by automatic real-time weigh-in-motion[J].Journal of Structural Mechanics and Earthquake Engineering,2004,69(773):99-111.
[10] O’Brien E J,Znidaric A,Ojio T.Bridge weigh-in-motion:latest developments and applications worldwide[C]//B Jacob,et al.Proceedings of the International conference on heavy vehicles.Paris,France:John Wiley,2008.25-38.
[11]王宁波,任伟新,李 苗.基于影响线的桥梁移动荷载识别[J].振动与冲击,2013,32(3):136-140.
WANG Ning-bo,REN Wei-xin,LI Miao.Moving loads identification of bridge based on influence line[J].Journal of Vibration and Shock,2013,32(3):136-140.
[12] Zhu X Q,Law S S.Bridge dynamic responses due to road surface roughness and braking of vehicle[J].Journal of Sound and Vibration,2005,282:805-830.

