钢悬链线输流立管顶部浮体激励非线性响应研究

孟 丹

(青岛理工大学 土木工程学院，青岛 266033)

随着海洋石油开采水深的增加，钢悬链线立管(Steel Catenary Riser)成为深海油气资源开发的首选立管形式。1994年安装了世界上第一条钢悬链线立管，引起了工程界和学术界的极大关注［1-5］。以往对深水海洋立管这种细长的柔性结构多采用大位移小应变的分析方法，而实际上即使对于伸展性不明显的立管结构，大应变的影响都不可忽视［6］。小应变的假设只适用于应变量相对于单元长度来说足够小的情况，对于深水细长立管，这种假设很难满足设计计算中精度的要求。在波浪和流的作用下，不仅上部浮体产生的复杂动力响应会作用于钢悬链线立管［7-9］，立管本身也承受着强度相当大的波浪和流的作用力。而在分析计算中，都是将外部流体的非线性作用力进行线性化，甚至忽略流体阻尼的影响，不能反映外部流体对立管振动的实际影响。准确地预报出实际海况中钢悬链线立管的动力响应问题，对于逐渐向深海发展的海洋开采事业具有重大的意义［10］。

因此，本文考虑深水钢悬链线立管大应变的特性以及内流和外部流体的影响，采用具有弯曲刚度的细长梁模型模拟钢悬链线立管，利用Hamilton原理和拉格朗日应变理论建立了立管的二维动力学模型，探讨了在顶部浮体激励影响下立管的动力响应。

1 钢悬链线立管的动力学模型

图1给出了典型的上部连接于浮体的自由悬挂钢悬链线立管的构型图，水深为xH，顶部的静止偏移为yV。立管顶端作用有初始的拉力Tt以保持立管的初始构型。图中定义了立管的三种状态分别为初始态、平衡态以及动态。立管在初始状态下，由于其自重、内流的作用、轴向和弯曲变形达到平衡状态。同时，平衡状态被认为是立管动力学计算的初始状态。在外部荷载的作用下，立管会由平衡态发展到动态，u1、u2和u3分别为立管微元ds0从平衡态到动态在X、Y和Z方向上的位移。在本文的研究中，只考虑立管在XOY平面内的运动，即u3=0。

图1 钢悬链线立管大变形示意图Fig.1 Schematics of large deformations of steel catenary riser

立管轴向应变能Ua的变分表达式为:

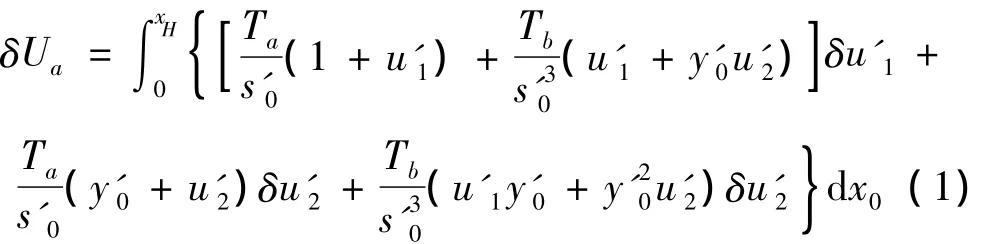
其中，Ta=EA0ε0，Tb=EA0;E为立管的弹性模量，A0为平衡位置立管的横截面积，ε0为平衡位置立管的应变。弯曲应变能的变分表达式为:

进行立管的动力分析，外力所做的虚功包括有效重力、外部流体以及惯性力所做的虚功［10］，其中由有效重力做的虚功可表示为:

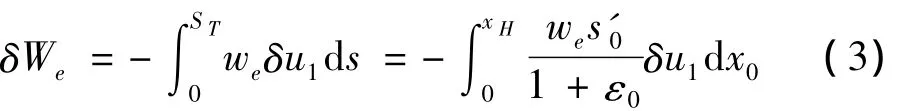
其中，we=(ρ+ρf-ρeA0)g，并且 ρ为初始位置单位长度管道质量，ρf为平衡初始位置单位长度内部流体质量，ρe为外部流体密度，g为重力加速度。

由外部流体做的虚功δWH可表示为:

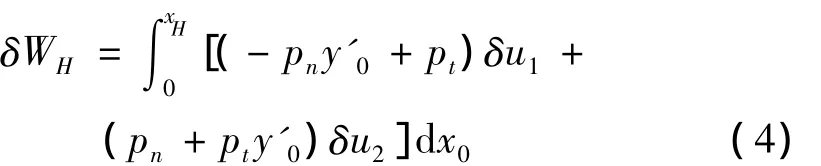
其中，pn、pt分别为外部流体作用在立管上的正压力、切向力［11］，在本文外部流体的参数分析中，假设外部流体为稳定流，在XOY平面内沿Y轴正向流动，且速度为U。以往针对钢悬链线立管顺流向动力响应的研究中，都将外部流体的作用力进行了线性化，本文为了考虑外部流体阻尼的影响，定义符号函数:

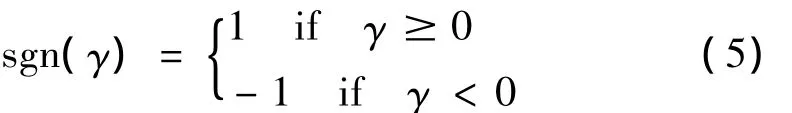
则pn、pt的表达式为:

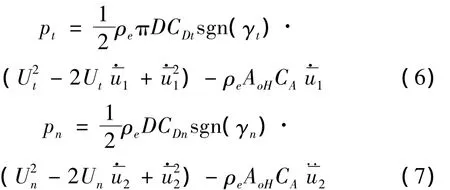
根据参考文献［10］给出的管道和内部流体的加速度的表达式，由惯性力做的功δWI可表示为:

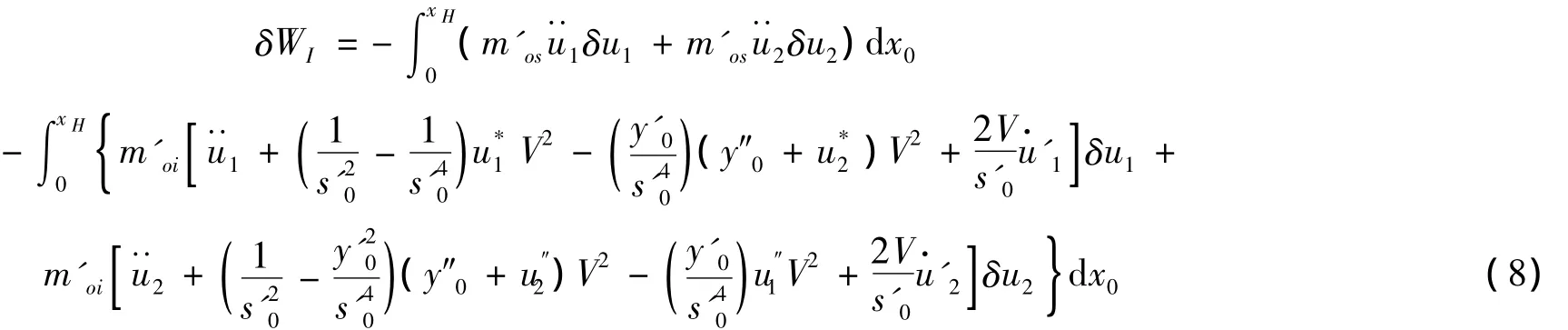
其中，m'os=ρs'0为平衡位置时单位长度管道的质量;m'oi=ρfs'0为平衡位置时单位长度内部流体的质量;V为立管内部流体的流速。

根据虚位移原理

可以得到动力学系统在虚位移δu1和δu2上的Euler’s方程，将立管在平衡位置的初始条件代入Euler’s方程可得系统在平衡位置处的静力平衡方程。由于平衡位置是系统进行动力分析的初始状态，所以联合静力平衡方程和Euler’s方程便可得到系统在XOY平面内的运动方程。

将水深xH分成n个长度为l的单元，则相对应的立管单元内任意一点的位移可表示为:

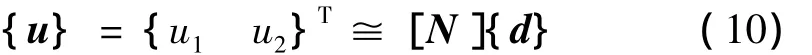
其中:

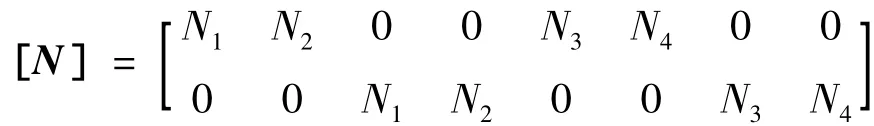
Ni为Hermit插值函数，

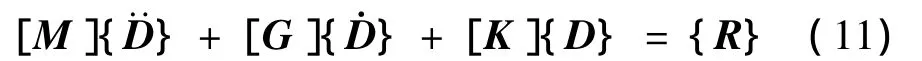
其中:［M］、［G］、［K］分别为整体质量矩阵、阻尼矩阵、刚度矩阵，表达式为:

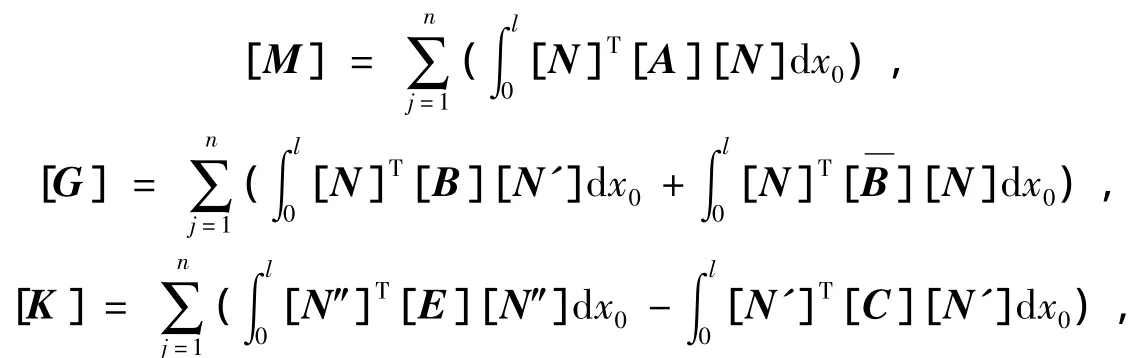
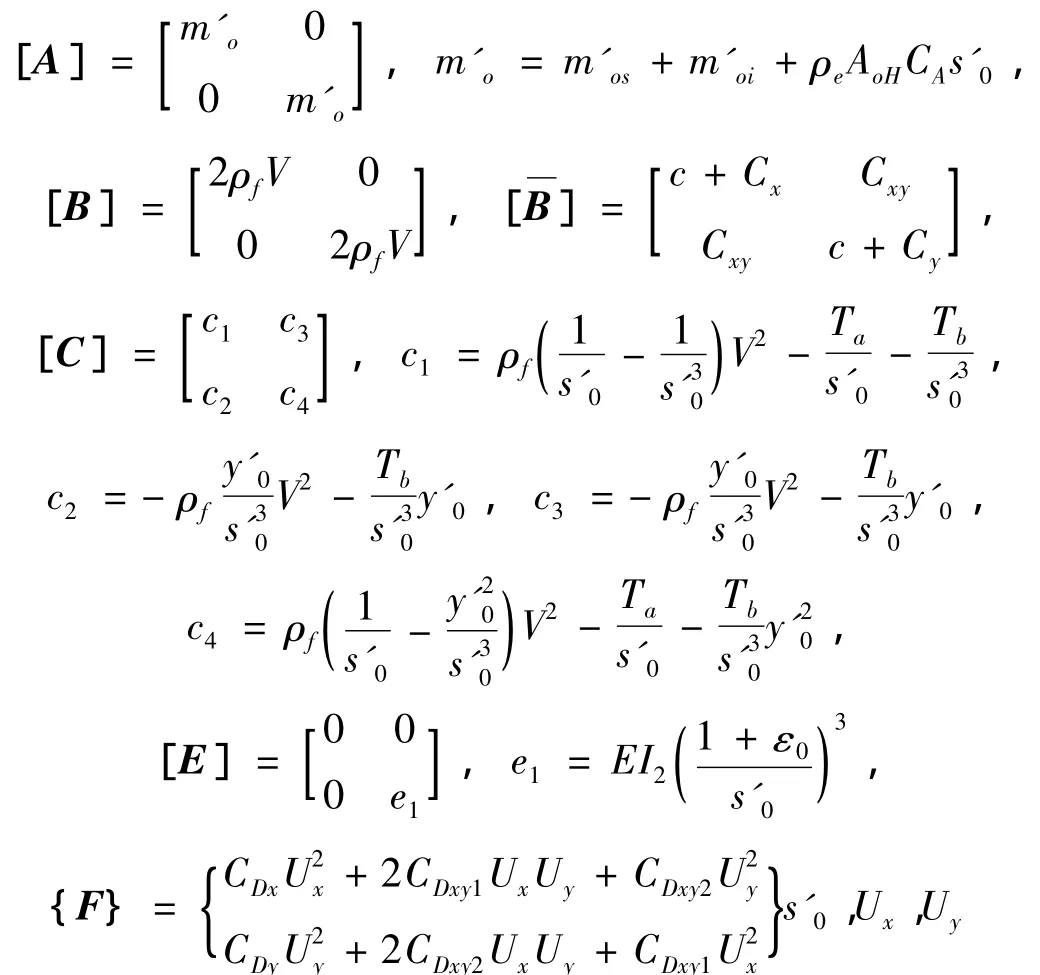
为外部流体在竖直和水平方向上的速度;

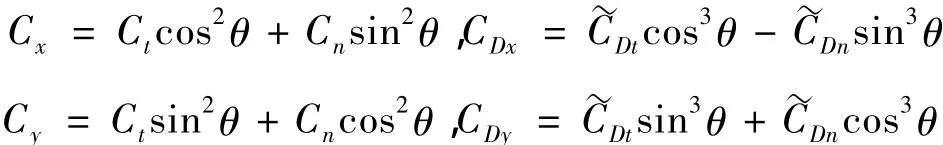
为竖直和水平方向上的流体阻尼和拖曳力系数;

Cxy=(Ct-Cn)sinθcosθ为x-y平面内等效水动力阻尼耦合系数，

为x-y平面内拖曳力耦合系数，其中:

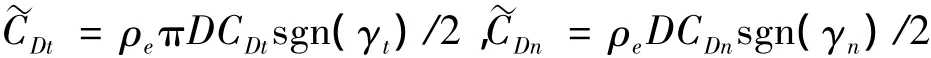
2 求解方法与模型验证

为了得到立管的动力响应，利用数值积分的方法，即Newmak-β法(积分参数γ=1/2，β=1/4)和Newton-Raphson迭代法对动力学方程进行求解。并用Matlab将上述算法编写程序resp.m来输出计算结果。

求解时立管底端的边界条件为

立管顶部的边界条件为

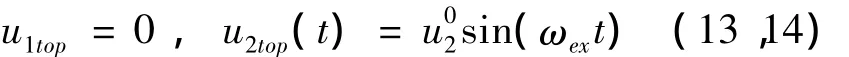
初始条件为

为了验证本文建立模型的正确性和保证下文计算结果的有效性，现将本文的计算结果与已有研究成果进行比较。文献［7］分别用有限差分法和REFLEX计算了二维钢悬链线立管在顶部浮体激励下的动力响应，文献采用的立管模型物理参数如表1所示。

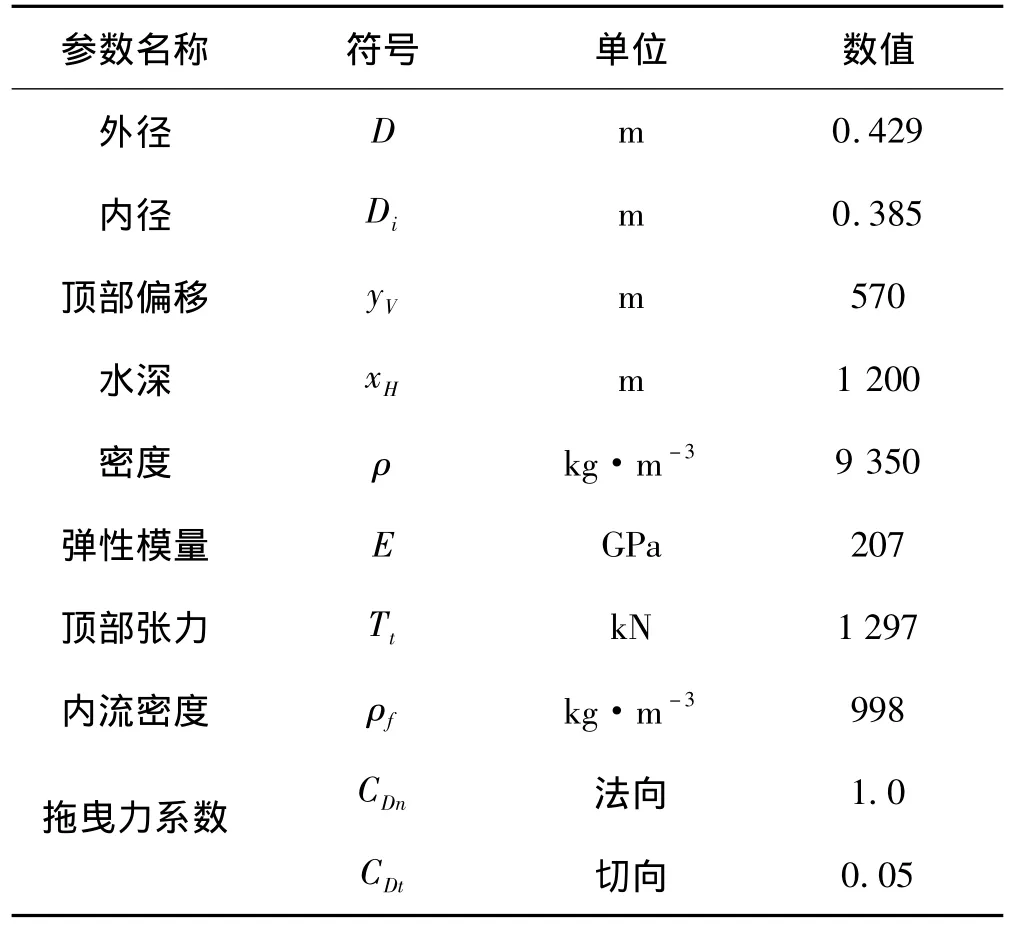
表1 立管物理参数Tab.1 Analysis input data

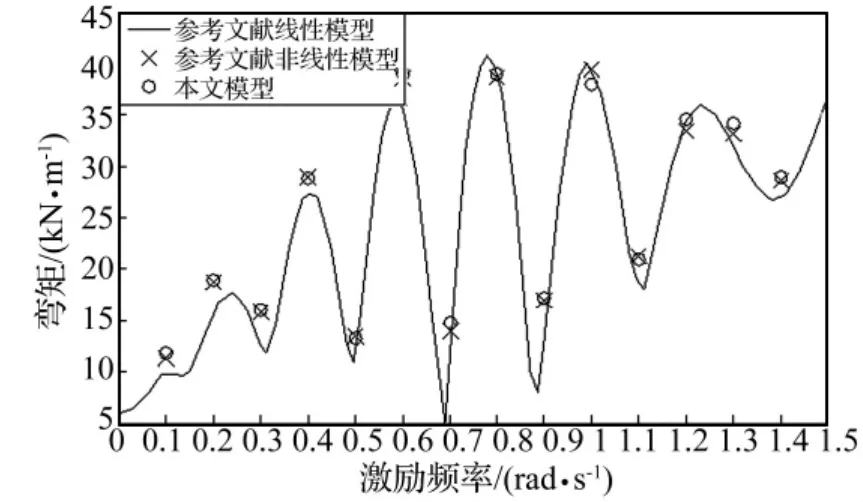
图2 MSBM处动弯矩结果比较Fig.2 Comparative results for the dynamic bending moment at the location of the maximum static bending moment

3 结果与讨论

由于已有研究成果计算中未考虑外部流体以及内流的作用。所以，以下内容将针上述模型在内外流体流动影响下的动力响应进行详细的分析，深入研究立管在弹性模量、内流流速以及外部流体流速等不同影响因素的作用下动力响应的变化情况。外部流体的参数为:海水密度 ρe=1 025 kg/m3，海流流速U=0 ～1.5 m/s，附加质量系数CA=1，惯性系数CM=2。

3.1 弯曲刚度的影响

本文建立的模型的另一个特点就是考虑了立管弯曲刚度对动力响应的影响，所以有必要分析有无弯曲刚度时立管的动力学行为。图3为不同激励频率时立管响应弯矩的包络线，图中虚线均为弯曲刚度为零时的动力响应。从图中可以看出，弯曲刚度存在对立管的动力响应幅值有一定的影响，特别是上下两端影响较大。对于立管顶部，ωV=0.4 rad/s时不考虑弯曲刚度计算所得的弯矩值约为考虑弯曲刚度时的1.4倍，ωV=1.1 rad/s时不考虑弯曲刚度计算所得的弯矩值约为考虑弯曲刚度时的1.5倍。

图3 弯曲刚度影响下立管沿水深动弯矩幅值Fig.3 The total bending moment along the riser under horizontal excitation demonstrated the effects of extensibility

3.2 内流流速的影响

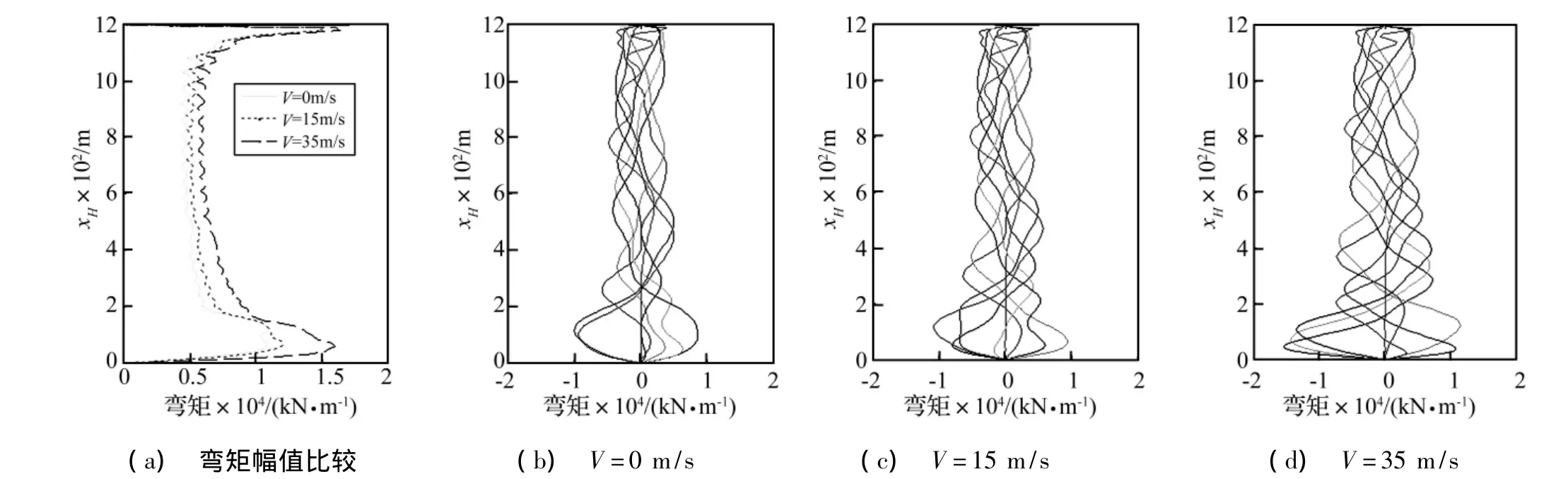
图4 不同时刻立管动弯矩分布图Fig.4 The total bending moment along the riser demonstrated the effects of internal fluid velocities

内流流速的变化会使立管的刚度产生变化［12］，进而影响立管在浮体激励下的动力响应。图4为Tt=2.5×1 279×103kN、ωV=0.4 rad/s时不同内流流速对立管浮体激励动力响应的影响。从可以看出，内流流速的增加使动弯矩幅值增大，特别是立管的底部弯矩增加的最明显，当流速达到35 m/s时，弯矩增大了约0.5倍。同时还可以看出流速增加使产生最大弯矩的位置向下移动。

图5为不同内流流速时立管底端和顶端的应力时程曲线，从中可以看出，动力响应经过一定的时间趋于问题。流速的变化对立管底端的应力值产生很大的影响，而对顶端却无明显的影响。

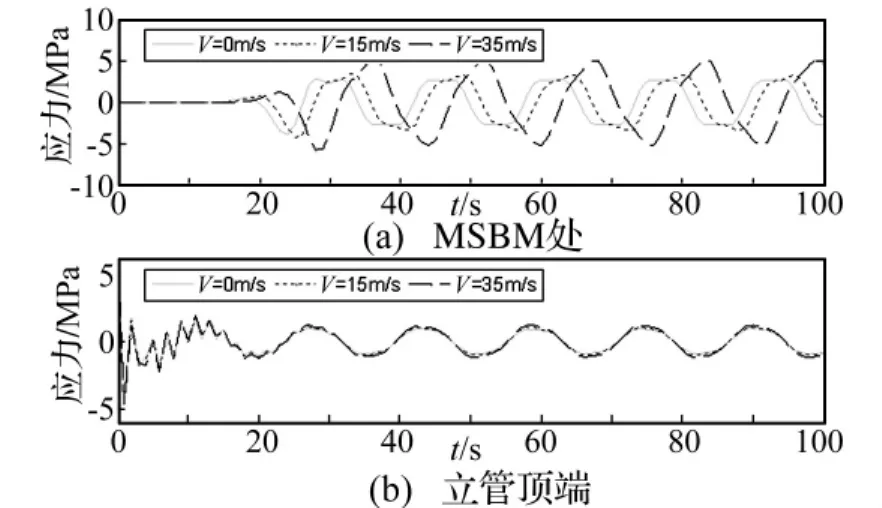
图5 不同内流流速时单元应力时程曲线Fig.5 Time history curve of stress at different internal fluid velocities

3.3 外部流体对动力响应的影响

外部流体的存在不但使钢悬链线立管产生附加质量，还会产生非线性拖曳力的作用，所以对其动力响应肯定会有影响。图6和图7分别为不同外流流速时立管动力响应的弯矩分布图和单元应力时程曲线。从图中可以看出，外流流速对立管底端的弯矩和应力的影响非常明显，如流速达到0.341m/s时，弯矩增大了约3倍，而对立管的其他部分影响很小。另外，与以上影响因素不同的是，外流流速增大会使立管底端由原来的正负应力交替出现变为正应力大小的交替变化，从图7中可以明显的反映出来。

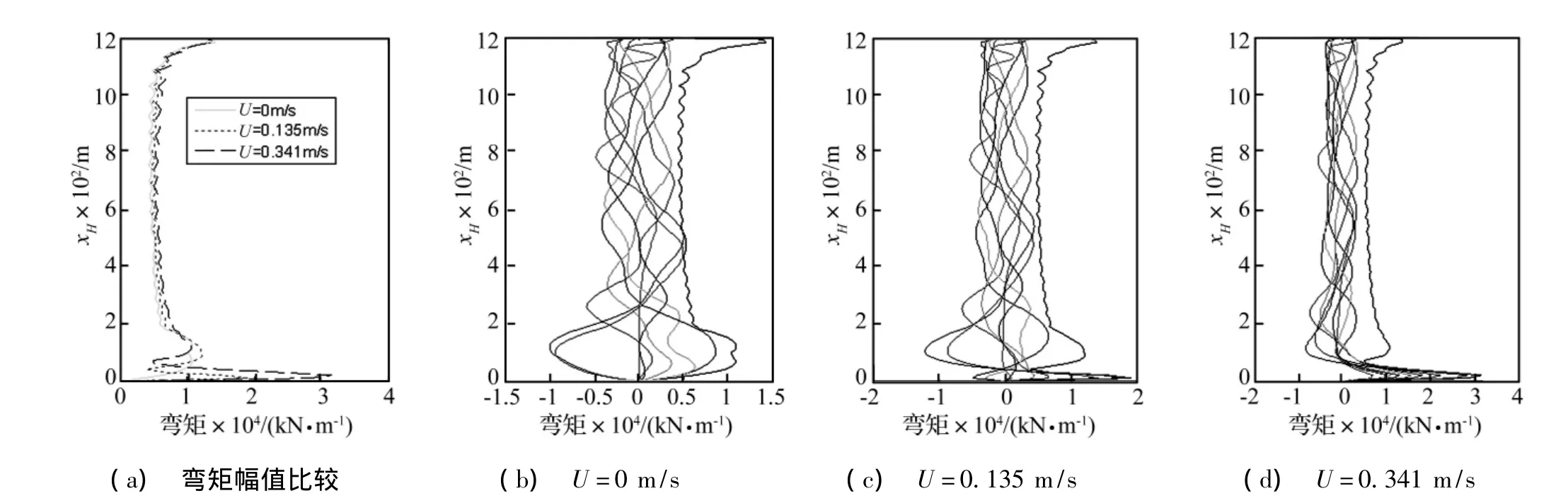
图6 不同时刻立管动弯矩分布图Fig.6 The total bending moment along the riser demonstrated the effects of external flow velocity

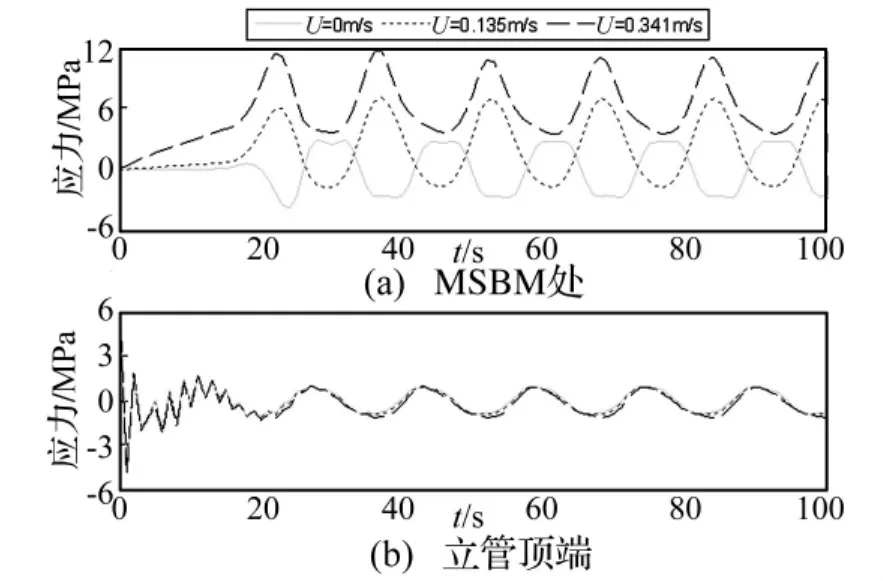
图7 不同外流流速时单元应力时程曲线Fig.7 Time history curve of stress at different external flow rate

4 结论

本文详细分析了弹性模量、内流流速和外部流体对立管在上部浮体激励下动力响应的影响。结果表明，本文建立的动力学模型在分析钢悬链线立管XOY平面内的运动特性是有效的。并且，立管的动力分析设计需要考虑各种因素的影响。

钢悬链线立管弯曲刚度存在与否对立管动力响应的影响很大，特别是上下两端。内流的变化使立管的浮体激励响应产生变化，随着内流流速的增加，立管底部的弯矩明显变大;外部流体的存在不但使钢悬链线立管产生附加质量，还会产生拖曳力的作用，所以对其动力响应产生影响。外流流速对立管底端的弯矩和应力的影响非常明显，对立管的其他部分影响很小。另外，与弯曲刚度和内流等影响因素不同的是，外流流速增大会使立管底端由原来的正负应力交替出现变为正应力大小的交替变化。

［1］ Giertsen E，Verley R，Schroder K.CARISIMA a catenary riser/soil interaction model for global riser analysis［C］.Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering(OMAE)，2004，1:633-640.

［2］ Dantas C M S，de Siqueira M Q，Ellwanger G B，et al.A frequency domain approach for random fatigue analysis of steel catenary risers at brazil's deep waters［C］.Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering(OMAE)，2004，1:199-209.

［3］金庆焕.深水油气是当今海洋油气勘探的主要热点［J］.科学中国人，2006，(11):18-19.

JIN Qing-huan.Deepwater oil and gas is the main interest of today's offshore oil and gas exploration［J］.Scientific Chinese，2006，(11):18-19.

［4］李清平.我国海洋深水油气开发面临的挑战［J］.中国海上油气，2006，18(2):130-133.

LI Qing-ping.The situation and challenges for deepwater oil and gas exploration and exploitation in China［J］.China Offshore Oil and Gas，2006，18(2):130-133.

［5］ Mekha B B.New frontiers in the design of steel catenary risers for floating production systems［J］.Journal of Offshore Mechanics and Arctic Engineering， 2001， 123:153-158.

［6］ Chucheepsakul S，Monprapussorn T，Huang T.Large strain formulation of extensible flexible marine pipes transporting fluid［J］.Journal of Fluids and Structures，2003，17:185-224.

［7］ Leklong J， Chucheepsakul S， Kaewunruen S. Dynamic responses of marine risers/pipes transporting fluid subject to top end excitations［C］.Proc of 8th ISOPE Pacific/asia Offshore Mech Symposium，2008，105-112.

［8］ Chatjigeorgiou I K.A finite differences formulation for the linear and nonlinear dynamics of 2D catenary risers［J］.Ocean Engineering 2008，35:616-636.

［9］Irani M B，Modi V J，Welf F.Riser dynamics with internal flow and nutation damping［C］.Proceeding 6th International Offshore Mechanics and Arctic Engineering Conference，1987，3:119-125.

［10］林海花，王言英.波流共同作用下隔水管动力响应非线性分析［J］.船舶力学，2009，13(2):189-195.

LIN Hai-hua， WANG Yan-ying. Analysisofnonlinear dynamic responses for marine riser induced by waves and currents［J］.Journal of Ship Mechanics，2009，13(2):189-195.

［11］ Chakrabarti，S K.Nonlinear Methods in Offshore Engineering［M］.Amsterdam Elsevier，1990.

［12］ Meng D，Guo H Y，Xu S.Nonlinear dynamic model of a fluid-conveying pipe undergoing overall motions［J］.Applied Mathematical Modelling，2011，35:781-796.