某牵引车共振问题测试及研究

卜绍先，谭松涛，闵 鹏，高中美，焦安勇

(中国重汽集团技术发展中心计算分析所，济南 250002)

工作模态测试及分析是利用自然激励，如车辆受路面、发动机和风力激励，然后采集输出数据，分析系统的实际工况。近40多年来，通过实验及数据处理来识别实际结构的动力学模型是结构动力特性研究方面的一个重要发展。实验模态分析方法与计算模态分析方法一起，成为解决现代复杂结构动态特性设计的相辅相成的重要手段。应用模态分析方法，人们有可能把复杂的实际结构简化成所谓模态模型，来进行系统的响应计算，从而大大简化系统的数学运算。因而，本文仅采集一辆牵引车共振状态时的整车数据，然后研究其振动特性［1-4］。

1 理论算法

1.1 分析方法

在无法测量输入信号的情况下，假定激励信号为白噪声，从而用各自输出信号的自相关和互相关函数替代冲激响应函数进行模态参数识别［1］。

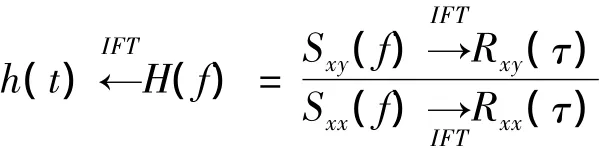
其中，H(f)为响应h(t)的傅氏变换，Sxy(f)为时域响应信号互相关函数Rxy(τ)的傅氏变换，Sxx(f)为时域响应信号互相关函数Rxx(τ)的傅氏变换。实际上，不会有真正的白噪声激励。只要是有色噪声激励，或脉冲激励，都有可能在激励源的频率范围内得到良好的分析结果。

1.2 SCE － LSFD 法［5－7］

1.2.1 用 LSCE(Least Square Complex Exponential)法求极点

将自相关和互相关函数视为包含Nm个模态的衰减正弦分量之和:

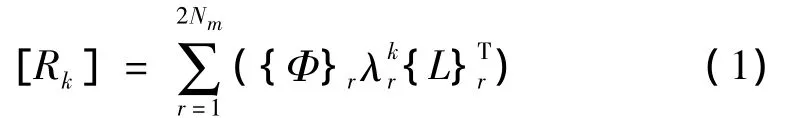
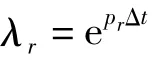
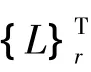
1.2.2 用 LSFD(Least Square Frequency Domain)法求模态振型

用LSCE法求得极点pr的基础上，再用LSFD法求模态振型{Φ}r。拟合函数不再是频响函数，而是自功率谱Smm(ω)和互功率谱Smn(ω)。新用的参考关系式为:

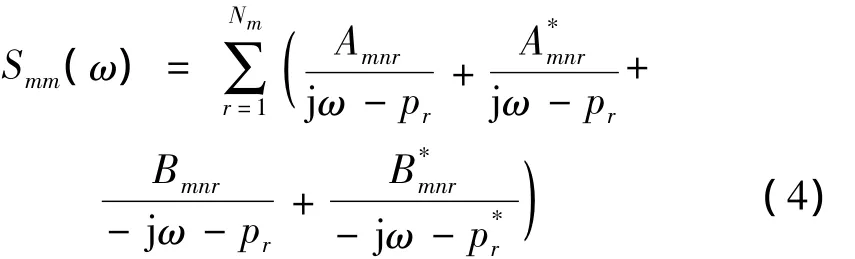
在自功率谱情况下，m=n，Amnr=Bmnr。留数Amnr正比于模态振型{Φ}r的第m个元素，而留数Bmnr则正比于{Φ}r的第n个元素。通过拟合所有测点与某一参考点之间的互功率谱，便可得到完整的模态振型。

2 测试及分析

数字采集器比利时的LMS SCANDⅢ，加速度传感器美国PCB 315A16，数据采集及处理系统都使用比利时的LMS Test.Lab9A。频宽为256 Hz，频率分辨率取0.062 5 Hz。

2.1 测试工况

2.1.1 载荷

空载(9.85 t)，即仅牵引头，这是一种常用工况;满载(45.5 t)，即带上挂车且装满载荷，这也是一种常用工况。

2.1.2 车速

经过初步的诊断，得知该车的共振现象仅出现在2个速度段，因此，仅考虑出现共振现象的车速。两种载荷下需要采集数据的车速如表1。

表1 测试车速及载荷情况Tab.1 Conditions of testing velocity and load

2.2 响应点布置

如图1所示，根据测试要求，在整车的驾驶室、车架、车桥和传动系上共布置27个测试点。

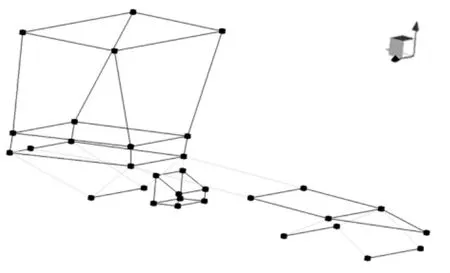
图1 测试点布置示意图Fig.1 Layout of testing points

2.3 工作模态分析

根据测试的各个车速的所有互谱和参照点自谱，求出总和，然后分析SUM PSD(Power Spectral Density)的特性和求出共振状态的模态频率和振型，从而判断出振源的位置。

2.3.1 整车总功率谱密度曲线分析

由图2可知，空载时，共振最强烈出现在两个车速时，即30 km/h和80 km/h，且频率分别为4.16 Hz和11.94 Hz，这与人为感觉的振动强烈程度相一致。

由图3可知，满载时，共振最强烈出现在两个车速时，即25 km/h和75 km/h，且频率分别为3.43 Hz和11.05 Hz，这与人为感觉的振动强烈程度相一致。

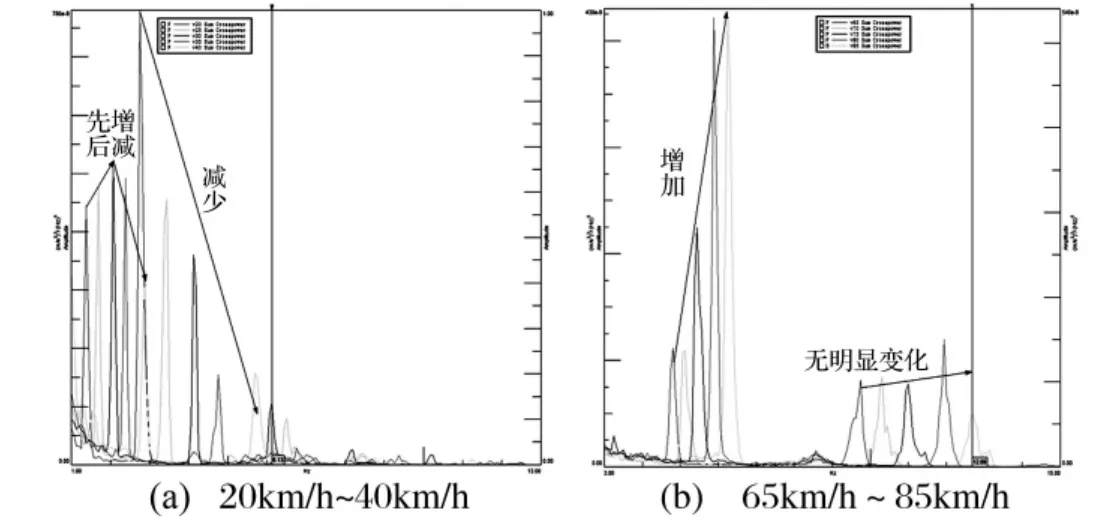
图2 空载时总功率谱密度曲线Fig.2 Sum of PSD at the unloaded condition

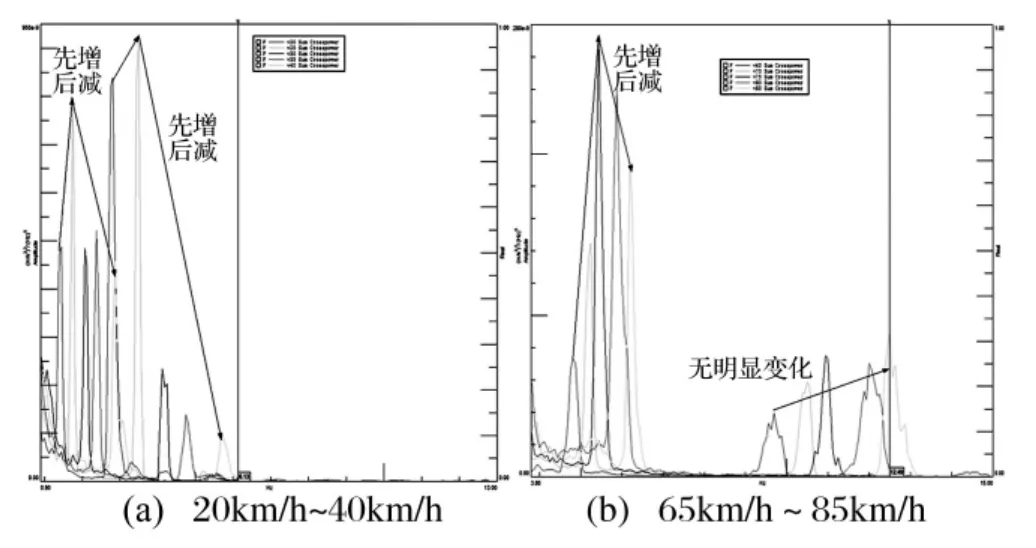
图3 满载时总功率谱密度曲线Fig.3 Sum of PSD at the loaded condition

2.3.2 共振状态的模态频率和振型

运用上述LSCE-LSFD算法分别求出空载和满载状态下共振的模态频率和振型(如表2)，模态振型动画分别如图4和图5。

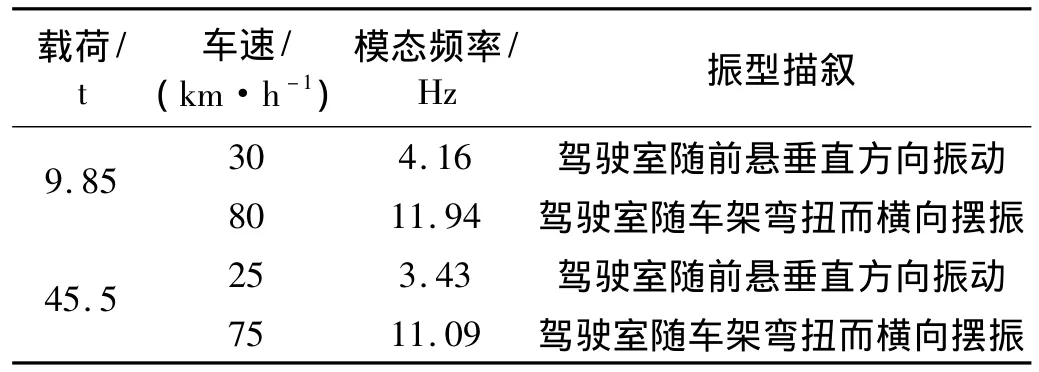
表2 模态频率及振型描述Tab.2 Modal frequency and description of mode shape

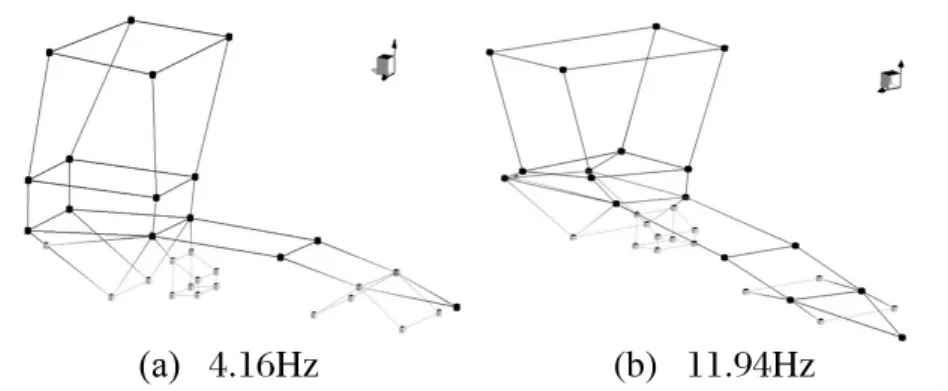
图4 空载时共振的模态Fig.4 Mode of resonance at the unloaded condition

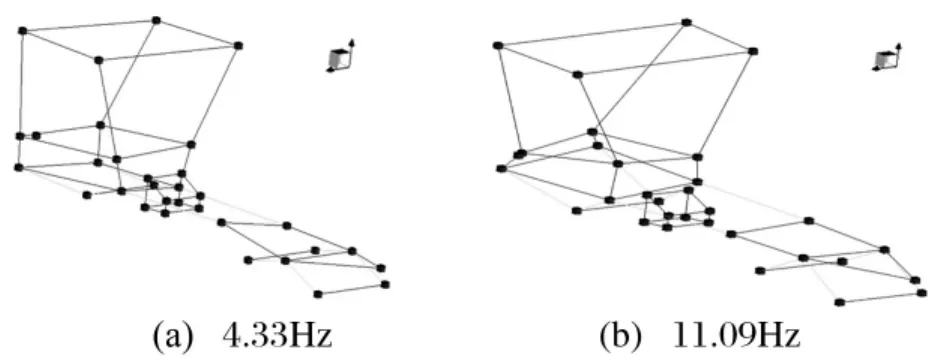
图5 满载时共振的模态Fig.5 Mode of resonance at the loaded condition

2.3.3 激励源的确定

统计出各个车速下总PSD的峰值与车桥两端的激励频率相比较如图6所示。车桥的1倍频率与总PSD图上的第1个峰对应频率一致，车桥上2倍频率与总PSD图上的第2个峰对应频率一致。因此，判断引起该车共振的激励源来自车桥。

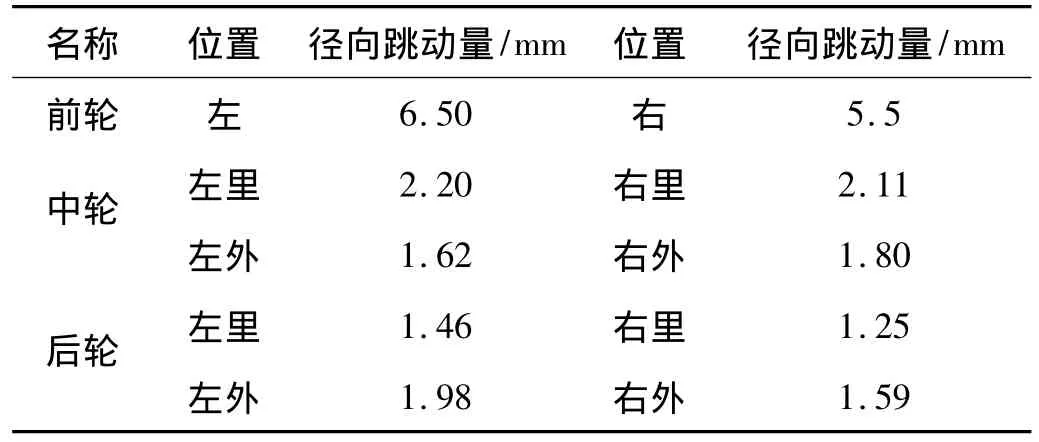
表3 车轮径向跳动量测量记录Tab.3 Measuring record of tires’radial fluctuation

图6 车桥激励频率和模态频率与车速的关系Fig.6 Relation of axle’s exciting frequency and modal frequency with velocity of vehicle

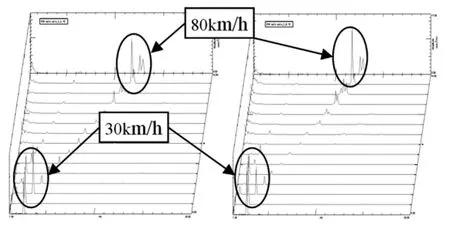
图7 空载时前桥左右PSD瀑布图Fig.7 Compare of the left and right ends’PSD waterfall of the front axle at the unload condition

由瀑布图7、8和9可知，前桥左右的PSD曲线峰值与整车总PSD的峰值相一致，在车速为30km/h和80km/h时幅值最大，而第2、3桥却没有这个特征。因此，可以判定空载时引起共振的激励源就是前桥。

同样，可以判定满载时引起共振的激励源也是前桥。

参照国标GB QC/T 717-2004《汽车车轮跳动量的要求和检测方法》，对该车所有车桥两端轮毂和车轮总成的径向跳量进行了测量。

发现轮毂的跳动量在设计要求内，而车轮径向跳动量数据记录如表3所示。前轮径向跳动量超过行业标准值(2.2 mm)150%以上，参照国标GB/T 18506-2001《汽车轮胎均匀性试验方法》，这种失圆会使车轮在行驶过程中径向波动力幅值过大，当它的频率频率与前悬架和后悬架偏频一致时就会产生共振。

2.3.4 验证

更换两条满足要求的新车轮，重复以前的工作模态测试，数据处理的结果如下图10-13。由图12、图13瀑布图可知，更换车轮后PSD峰值远远小于更换车轮前;由图10、图11中PSD曲线可知，空载时峰值消失，即共振现象也消失。

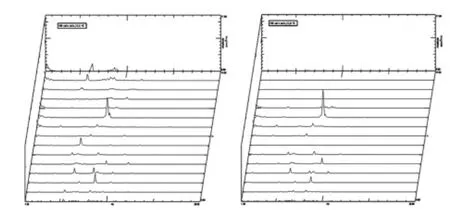
图8 空载时第2桥的左右PSD瀑布图Fig.8 PSD waterfall of the second axle at the unload condition

图9 空载时第3桥的左右PSD瀑布图Fig.9 PSD waterfall of the third axle at the unload condition

图10 空载时低速段的总PSD更换前后对比Fig.10 Compare of the sum PSD of fore-and-aft change at the low velocity and unloaded condition

图11 空载时高速段的总PSD更换前后对比Fig.11 Compare of the sum PSD of fore-and-aft change at the high velocity and unloaded condition

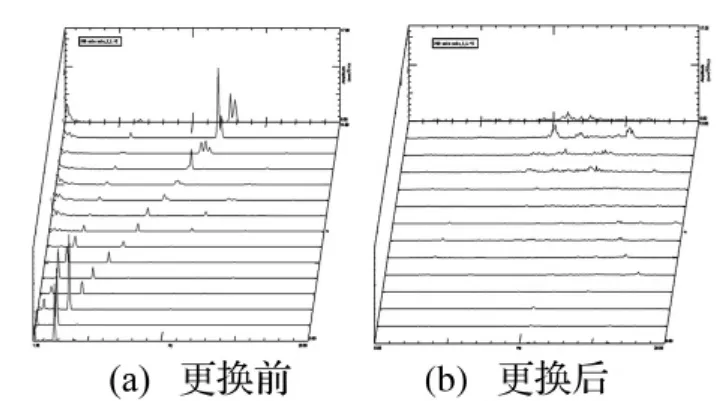
图12 空载时前桥左边的PSD瀑布图更换前后对比Fig.12 Compare of the front axle’left PSD waterfall of fore-and-aft change at the unloaded condition

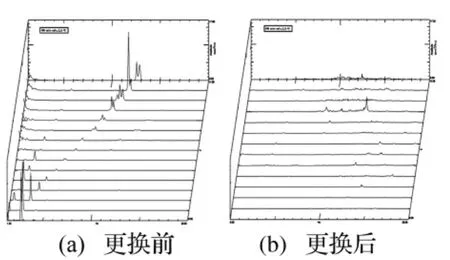
图13 空载时前桥左边的PSD瀑布图更换前后对比Fig.13 Compare of the front axle’right PSD waterfall of fore-and-aft change at the unloaded condition

同样，满载时对整车进行工作模态测试验证，共振现象也消失。

3 结论

该论文详细阐述了工作模态测试理论及方法，并运用该技术成功地解决了一辆牵引车存在的典型共振问题。因此，总结出以下几个结论:

(1)运用工作模态测试及分析可以得到共振状态的振型和频率;

(2)通过多个车速和多个测试点的PSD曲线的对比分析，可以判断出该车共振的激励源位置;

(3)人为感觉振动强度与系统总功率谱密度曲线上峰值的高低相一致。

［1］ LMS.Operational modal analysis［M］.9A，2008.

［2］李德葆，陆秋海.实验模态分析及其应用［M］.北京:科学出版社，2001.

［3］管迪华.模态分析技术［M］.北京:清华大学出版社，1996.

［4］沃德·海伦，斯蒂芬·拉门兹，波尔·萨斯［M］.北京:北京理工大学出版社，2001.

［5］ Peeters B，Vanhollebeke V，Van der Auweraer H.Operational PolyMAX for estimating the dynamic properties of a stadium structure duringa footballgame［C］//Proceedingsof International Modal Analysis Conference 23，Orlando，FL，USA，January-February，2005.

［6］Janssens K，Kollar Z，Peeters B，et al.Order-based resonance identification using operational PolyMax［C］//Proceedings of International Modal Analysis Conference 23，Orlando，FL，USA，January-February，2005.

［7］Gupta A D，Santiago J M，Meyer C.Comparison of computational and experimental modal analysis of an armored vehicle hull with multiple access openings［J］.USA:Computers ＆Structures，1995，56(2/3):411-414.