基于解析解和边界元解的圆柱壳声辐射对比研究

张俊杰，原春晖，刘 彦，吴武辉

(中国舰船研究设计中心 船舶振动噪声重点实验室，武汉 430064)

圆柱壳结构在工程中广泛应用，其产生的振动和声辐射也越来越受到关注。圆柱壳结构的分析方法分为解析法和数值法。由于解析法仅能研究结构形式简单的圆柱壳，对于工程中复杂的圆柱壳，一般采用数值解法。在中低频频段，数值解法一般是采用有限元和边界元联合的方式。其计算流程一般是:① 建立复杂壳体结构有限元模型，施加边界条件并计算;② 提取壳体表面网格作为边界元网格;③ 提取壳体外表面的法向位移;④ 将边界元网格和法向位移导入到边界元软件中计算，得到相关的声学参量。详细计算流程见文献［1］。上述求解过程清晰，简单易行，国内外学者运用有限元和边界元联合分析了圆柱壳结构的振动和声辐射。

商德江等［2］运用有限元和边界元分析了加肋双层圆柱壳在受点力激励作用的声辐射特性，并运用有限元和解析解比较了弹性球壳在轴对称点力激励下表面法向位移和表面声压分布。徐张明等［3］运用有限元和边界元分析了带浮筏装置的水中双层加了圆柱壳振动和噪声，文中对长方体声腔和椭圆球壳简单结构运用编程和边界元软件计算进行了声振对比，而对于带浮筏装置复杂圆柱壳采用有限元软件和边界元软件联合处理方式。贺晨等［4］运用有限元、边界元和统计能量分析方法对圆柱壳在流场中振动和声辐射效率进行了计算，文中运用边界元和解析解比较了空气中圆柱壳的辐射效率，两者得到的结果在中低频率相差较大。其他作者如石焕文［5］、曹贻鹏［6］、陈海龙［7］和姚熊亮［8］也用有限元和边界元对单层圆柱壳，双层圆柱壳等壳体结构的振动和声辐射进行了研究。

在上述文献中，边界元计算一般是假设每个波长六个单元线性单元或三个二次单元［9］以确定最大可以计算频率，并没有考虑不同加载方式—基于单元(Element)加载和基于节点(Node)加载对计算结果的影响，以及这两种方式网格加密后收敛的问题。事实上，这两种加载方式对计算结果以及网格加密的收敛性问题有较大影响。基于此，本文针对工程广泛应用的圆柱壳结构，通过与解析法对比，探讨了边界元两种加载方式对声辐射影响，以及网格加密的收敛性问题，得到一些对工程有益的结论。

1 模型简介和理论计算

1.1 模型简介

流场中简支在无限障板上有限长圆柱壳的几何、材料参数和坐标系如图1所示。圆柱壳半径为R，长度为L;流场中声速和密度分别为c0和ρ0;壳体杨氏模量、泊松比和密度分别为E1、v1和ρ1。分别用r，θ和 x表示柱坐标系的径向、周向和轴向，w，v和u表示这三个方向的位移分量。

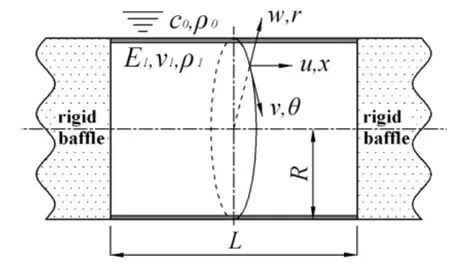
图1 有限长圆柱壳几何、材料参数和坐标系Fig.1 Geometry material parameters and coordinate system of finite cylindrical shell

1.2 圆柱壳运动方程

对于理想流体中受法向激励力作用的单层圆柱壳，为了便于求出壳体的法向位移，给出用阻抗表示的法向位移的关系式为［10－11］:

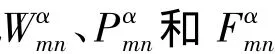
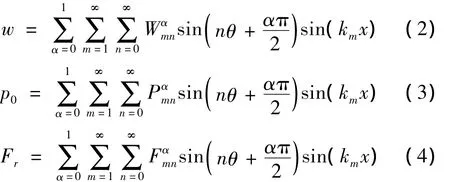
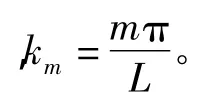
1.3 流场声压推导

理想流体中，流场中的声压满足Helmholtz方程，壳体和流场边界处满足位移的连续方程。运用傅立叶变换，最后得到时域中声压表达式:

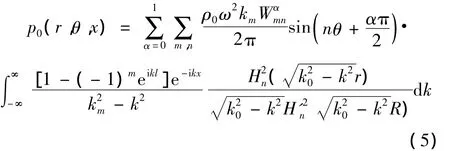
若不考虑轴向模态耦合，把式(5)代入式(3)，运用三角函数的正交性得到(r=R)

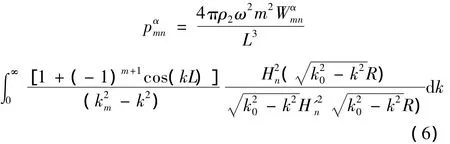
为方便计算，无量纲化。设λ*=kR，k*=k0R，则式(6)可以变为:

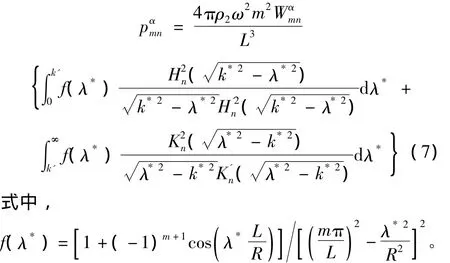
为了加快计算速度，可以对式(7)进行变量替换，具体可以参考文献［11］。

1.4 作用力

考虑点激励作用，且激励力作用在壳体内表面，沿着径向。点激励运用式(3)模态展开后的系数

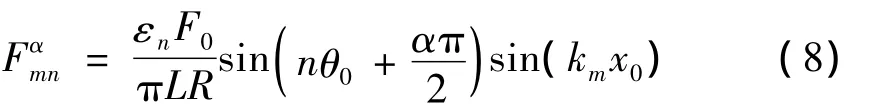
式中:n=0时εn=1;n≥1时εn=2，F0外力幅值，x0和θ0分别是外力在轴向和周向的作用位置。

1.5 耦合方程求解

把式(6)和式(8)代入式(1)，便可以求出对应于模态(m，n)的对称或者反对称法向位移，接着根据式(2)的算出壳体的位移w，以及根据式(6)和式(3)算出壳体和声场耦合面的声压p。

1.6 辐射声功率

一旦求出壳体的位移w和壳体与声场耦合面的声压p，辐射声功率便可以求出:

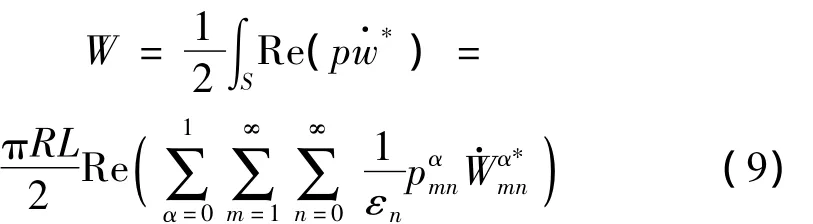
辐射声功率级定义为:

式中:W0=10－12W。

2 边界元计算

2.1 边界元基本方程

根据边界积分方程，把辐射面离散为小单元，并设离散后节点数目为N个，则节点处的声压ps与法向振速向量ws的关系式可以表示为:

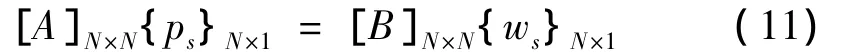
式中，矩阵［A］和［B］为影响矩阵，与振动面形状、流场属性和频率相关，与法向速度分布无关。

通过矩阵变换，式(11)可得到:

根据式(12)，一旦给定节点速度便可计算得到节点处声压，进一步可以得到辐射声功率。

2.2 辐射面的离散形式

对于工程复杂圆柱壳来说，声振解析解无法求出，需要借助数值解法。数值解法的一般求解过程是先在有限元软件中计算辐射面的振动速度，再将表面速度导入边界元中插值进行声场计算。有限元软件可选择性较多，如Ansys，MSC.Patran等，而声场计算一般是运用软件Sysnoise进行计算。Sysnoise软件提供了基于单元(Element)和基于节点(Node)的两种加载模式。

对于图1的壳体结构，圆柱面展开示意图如图2(a)。根据基于单元(Element)和基于节点(Node)的两种加载模式，以及考虑离散后节点数目大致相等的情况，图2(b－d)给出了典型三种分区形式。图中粗线表示单元的边界，小黑点表示边界元施加速度的位置。图2(b)是基于单元(Element)的加载形式，速度边界条件加载在单元中心位置上，单元速度分布均匀，等效为活塞运动。图2(c)－图2(d)是基于节点(Node)的加载形式，其中图2(c)的单元与图2(b)的单元位置和大小相同，只是速度边界条件加载在单元的节点上;图2(d)中单元节点的位置与图2(b)中施加速度位置(除去左右两侧)相同。

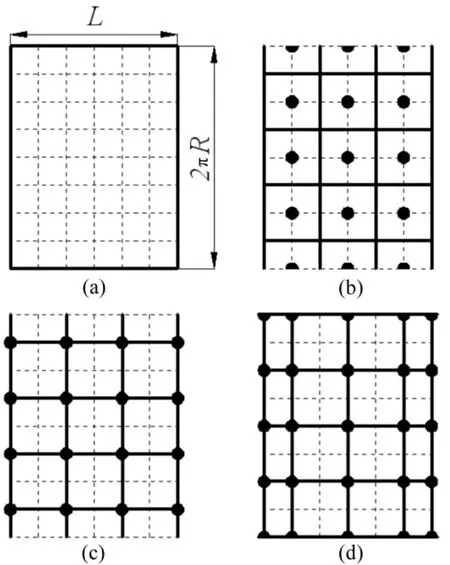
图2 壳体展开图及网格分区图Fig.2 Unfolded drawing and different meshes of cylindrical shell

3 数值计算及讨论

3.1 壳体几何、材料参数以及数值计算流程

3.1.1 壳体几何和材料参数

计算中壳体几何参数R=1 m，长度为L=3 m;流场中声速和密度分别为c0=1 500 m/s和ρ0=1 000 kg/m3;壳体杨氏模量E1和泊松比v1以纵波cd1、横波cs1和密度ρ1表示，其中纵波 cd1=cd(1+iζd)1/2，横波 cs1=cs(1+iζs)1/2，cd=5 800 m/s，ξd=0.001，cs=3 100 m/s，ξs=0.01 以及ρ1=7 850 kg/m3，激励力 F0=1 N。

3.1.2 解析解和边界元计算流程

边界元计算时壳体的表面位移从解析解中提取出来，解析解和边界元对比计算流程为:

(1)运用式(1)求解出有限长圆柱壳在激励力作用下的法向位移 Wαmn，运用式(9)求出壳体辐射声功率;

(2)从解析解的位移中提取出对应于图2(b－d)小黑点处的位移值;

(3)对应于图2(b－d)，生成边界元输入文件并计算得到辐射声功率;

(4)对比第(1)步和第(3)步的计算结果。

3.2 基于单元和基于节点的两种加载方式结果与解析解对比分析

按照工程经验，边界元单元大小要满足每波长六单元的基本要求。对于图2(b－d)的分区形式，除非特殊说明，其边界元网格的分区大小分别为20×40分区、20×40分区和21×40分区。按照这个要求计算出来的频率是1 593 Hz。在下面的数值计算中，讨论的频率范围为［0，1 000 Hz］，因此，按照每波长六单元的的要求结果是收敛的。下面分别就单个周向模态激励和所有周向模态激励(点激励)时解析解和边界元计算结果进行对比讨论。

3.2.1 单个周向模态激励情形

首先比较了点激励的分量—某个周向模态激励的情形，此时只需令式(8)中某个单个周向模态激励有值，而其它周向模态激励为零，且在计算时式(1)的轴向模态m截断上限取为30。计算中点力作用位置为x0=3L/5和θ0=π/6，取周向模态n=1和n=2两种情况。其中边界元计算考虑了图2(b－d)分区和加载的情况。解析解和边界元的结果分别如图3－4。由于三种分网方式得到的结果画在一幅图上不清晰，这里在保持坐标轴不变的情况下分别与解析解对比给出。需要说明的是，图中曲线指向横轴的阴影区域表示这个区间段算出的声功率为负值，这与实际情况不符，称该阴影区域为该方法“不可计算频率范围”，该“不可计算频率范围”是由于边界元计算中奇异性引起的。

单一周向模态激励时，壳体表面的速度变化平缓，如图5是周向模态n=1频率为300 Hz时壳体表面速度实部沿轴向和周向分布图。此时在周向模态n=1和n=2，运用解析解和三种分区方式计算的辐射声功率如图3和图4所示。由图可知，三种分区计算结果除了“不可计算频率范围”，其它频率段与解析解的结果趋势保持一致。通过仔细比较曲线间的相对误差可知，图2(b)分区基于单元(Element)加载的结果要优于基于节点(Node)加载的结果。事实上，这不是个例，接下来讨论点激励时也是这个规律。

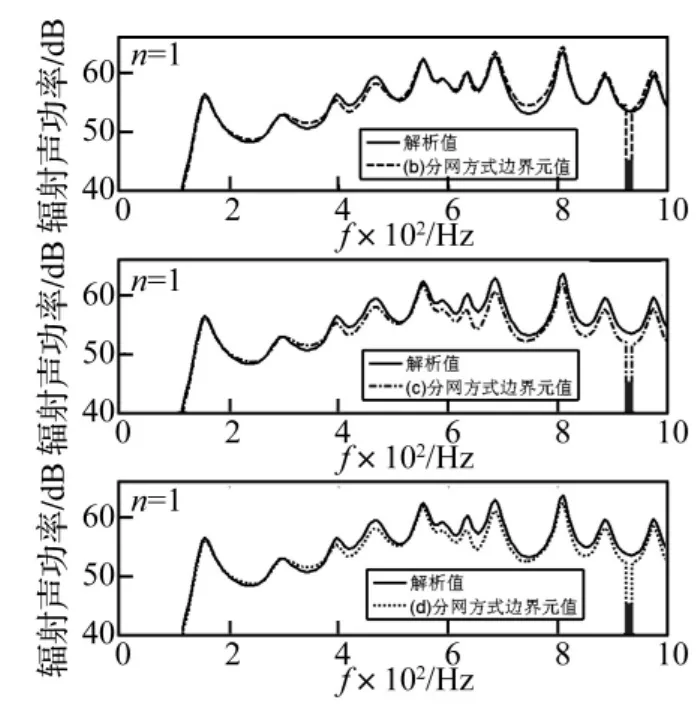
图3 周向模态n=1时解析和不同分区结果比较图Fig.3 The comparisons of analytical solution and results of different meshes with n=1

图4 周向模态n=2时解析和不同分区结果比较图Fig.4 The comparisons of analytical solution and results of different meshes with n=2

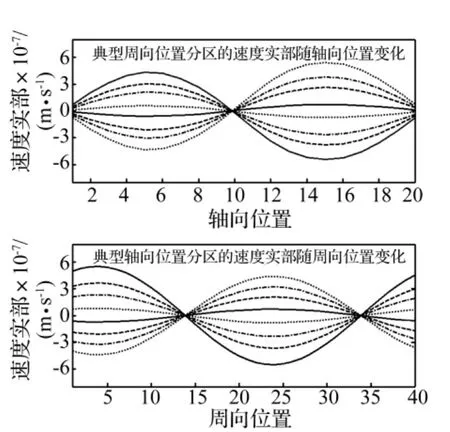
图5 周向模态n=1时速度实部沿轴向和周向分布Fig.5 The distribution of real part of velocity in axial and circumferential with n=1

3.2.2 所有周向模态激励(点激励)情形

点激励展开式式(3)包含所有周向和周向模态叠加，壳体表面的速度变化较大，如图6是单点激励情况下300 Hz时壳体表面速度实部沿轴向和周向分布图。

点激励计算时式(1)的轴向和周向模态m和n截断上限均取为30。不失一般性，给出了单点激励和两点同时激励时壳体辐射的声功率如图7和图8。单点激励位置为x0=3L/5和θ0=π/6;两个点力同时作用时激励位置分别为x0=3L/7和θ0=π/4，x0=3L/5和θ0=π/6。由图7－8可知，无论是从三种分区结果与解析解的相对误差，还是从“不可计算频率范围”的个数，图2(b)基于单元(Element)加载的结果明显要好于图2(c－d)基于节点(Node)加载的结果。对比图3－8可以推断，壳体表面速度分布越不均匀，图2(c－d)基于节点(Node)加载的结果可能与解析值差别越大，而图2(b)基于单元(Element)加载的结果与解析值接近程度与壳体表面速度分布基本无关。

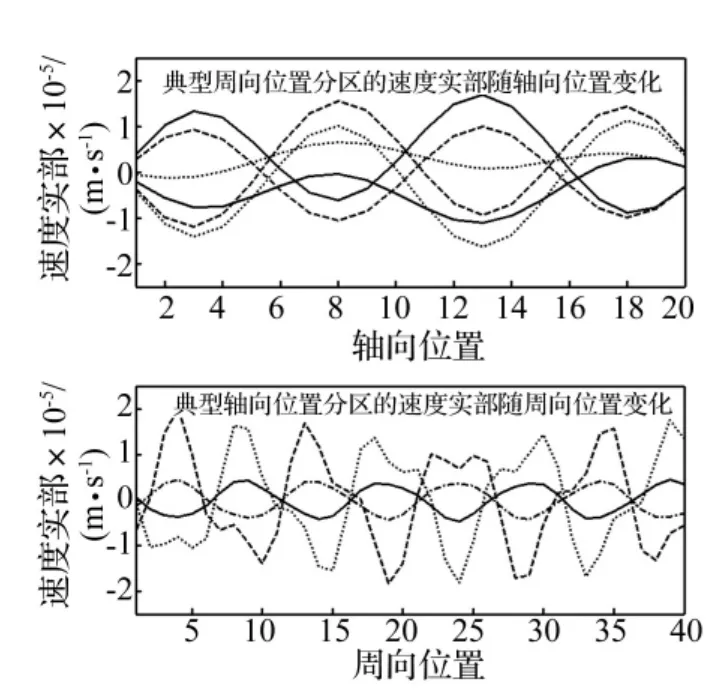
图6 点力作用下速度实部沿轴向和周向分布Fig.6 The distribution of imaginary part of velocity in axial and circumferential with a point force excitation

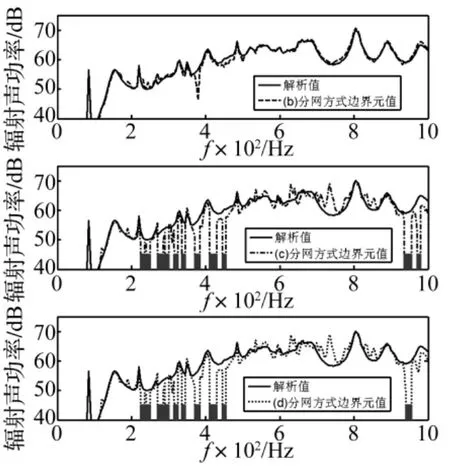
图7 一个点力作用下解析和不同分区结果比较图Fig.7 The comparisons of analytical solution and results of different meshes with a point force excitation

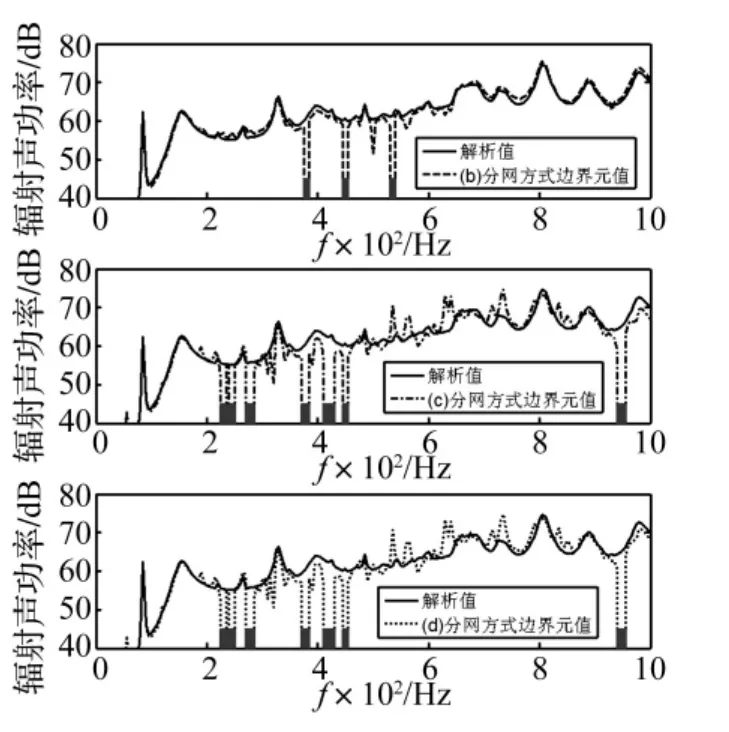
图8 两个点力作用下解析和不同分区结果比较图Fig.8 The comparisons of analytical solution and results of different meshes with two point force excitation

3.3 点激励下基于单元和基于节点的两种加载方式网格加密收敛性讨论

加密收敛性是讨论在已经满足了每波长六单元所要求的频率以内，分析图2(b－d)分区网格继续加密结果收敛性问题，也就是与解析值逼近的问题。选取的分区数目分别为16×32、20×40和30×60，三种分区方式每波长六单元对应的频率分别为1 275 Hz、1 593 Hz和2 388 Hz。计算中考虑的最高频率为1 000 Hz，是满足每波长六单元要求的。根据图7－8结论可知，基于节点加载的分区方式图2(c)和图2(d)的结果类似，因此这里仅选取图2(b－d)具有代表性的基于单元(Element)加载的图2(b)和基于节点(Node)加载的图2(c)。事实上，这两幅图的网格是一致的，只是加载方式不同。

图9 图2(b)分区网格加密收敛性Fig.9 The convergence of Fig.2(b)when refining the mesh

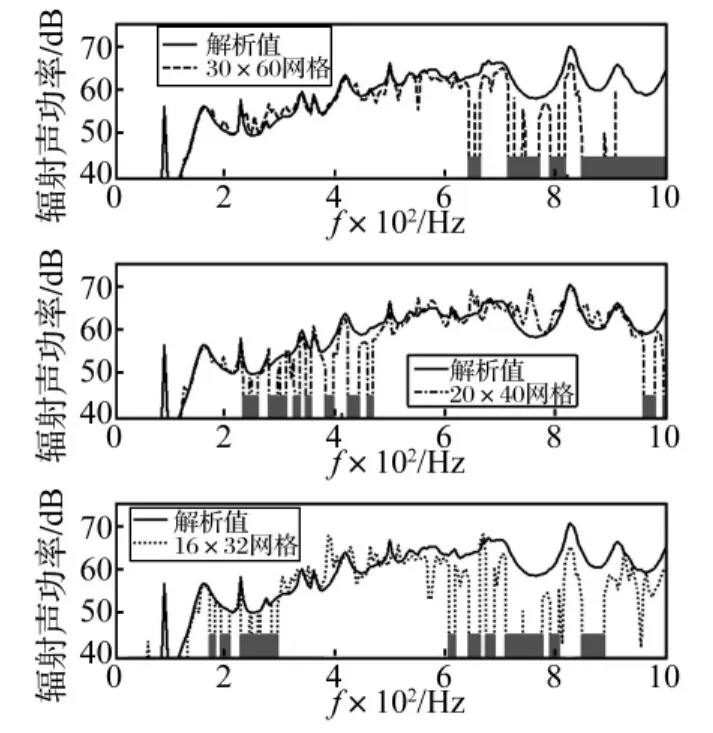
图10 图2(c)分区网格加密收敛性Fig.10 The convergence of Fig.2(c)when refining the mesh

图9和图10分别给出了图2(b)和图2(c)分区网格加密收敛性。由图9可知，随着网格细分，图2(b)基于单元(Element)加载的声功率与解析解越来越逼近，在网格30×60时几乎重合，这说明基于单元(Element)加载的方法在网格加密后具有很好的收敛性。而对于图10，在基于节点(Node)加载在网格加密后，在频段［0－150 Hz］是收敛的。在大于150 Hz的频段，不同分区数目出现了不同的“不可计算频率范围”。根据这个性质，可以试着划分不同的网格数量以避开“不可计算频率范围”，但是总的来说网格加密后不一定得到收敛结果。

4 结论

本文针对工程广泛应用的圆柱壳结构，在单元数目大致相等的情况下，通过与解析法的结果进行对比，探讨边界元了基于单元(Element)加载方式和基于节点(Node)加载方式对声辐射影响，以及这种加载方式网格加密的收敛性问题，得到如下结论:

(1)当壳体速度变化不大时，比如单个模态激励情形，基于单元(Element)加载方式和基于节点(Node)加载方式的计算结果与解析解计算结果基本一致，基于单元(Element)加载方式的结果要优于基于节点(Node)加载结果。

(2)当壳体速度变化较大时，比如单点激励或多点激励情形，基于单元(Element)加载方式的计算结果与解析解计算结果基本一致，而基于节点(Node)加载方式的结果与解析结果在部分频段相差较大，而且可能出现多个“不可计算频率范围”。

(3)壳体表面速度分布越不均匀，基于节点(Node)加载的结果可能与解析值差别越大，而基于单元(Element)加载的结果与解析值接近程度与壳体表面速度分布无关。

(4)当改变加密网格大小确定收敛性时，基于单元(Element)加载方式在网格加密后具有很好的收敛性;而基于节点(Node)加载方式并不一定得到收敛结果。

［1］王 晶，商德江.Ansys和Sysnoise之间的数据接口技术研究［J］.应用科技，2004，31(8):32－34.

WANG Jing，SHANG De-jiang.Study of the interface between ANYSYS and SYSNOIS［J］. Applied Science and Technology，2004，31(8):32 －34.

［2］商德江，何祚镛.加肋双层圆柱壳振动声辐射数值计算分析［J］.声学学报，2001，26(3):193－201.

SHANG De-jiang，HE Zuo-yong.The numerical analysis of sound and vibration from a ring－stiffened cylindrical double－ shell by FEM and BEM［J］.Acta Acustica，2001，26(3):193－201.

［3］徐张明.带浮筏装置的水中壳体模型振动、声辐射及其结构参数灵敏度研究［D］.上海:上海交通大学，2003.

［4］贺 晨，盛美萍，石焕文，等.圆柱壳体振动声辐射效率数值计算分析［J］.噪声与振动控制，2006，26(4):51－54.

HE Chen，SHENG Mei-ping，Shi Huanwen，et al.The numerical analysis of vibration and sound radiation efficiency from a cylindrical shell［J］.Noise and Vibration Control，2006，26(4):51 －54.

［5］石焕文，盛美萍，孙进才，等.加纵肋平底圆柱壳振动和声辐射的FEM/BEM研究［J］.振动与冲击，2006，25(2):88－92.

SHI Huan-wen，SHENG Mei-ping，SUN Jin-cai，et al.On FEM/BEM forthe problemsofvibration and acoustic radiation from an axially stiffened cylindrical shell with two end plates［J］.Journal of Vibration and Shock，2006，25(2):88－92.

［6］曹贻鹏，张文平.轴系纵振对双层圆柱壳体水下声辐射的影响研究［J］.船舶力学，2007，11(2):293－299.

CAO Yi-peng;ZHANG Wen-ping.A study on the effects of the longitudinal vibration of shafting on acoustic radiation from underwater double cylindrical shell［J］.Journal of Ship Mechanics，2007，11(2):293 －299.

［7］陈海龙，钱德进，计 方，等.静水压与阻尼覆盖层对圆柱壳声辐射的影响［J］.传感器与微系统，2009，28(3):42－44.

CHEN Hai-long，QIAN De-jin，JI Fang，et al..Effects of hydrostatic pressure and damping materialon acoustic radiation of cylindrical shell［J］.Transducer and Microsystem Technologies，2009，28(3):42 －44.

［8］姚熊亮，杨娜娜，陶景桥.双层壳体水下振动和声辐射的仿真分析［J］.哈尔滨工程大学学报，2004，25(2):136－140.

YAO Xiong-liang，YANG Nana，TAO Jing-qiao.Numerical research on vibration and sound radiation of underwater double cylindrical shell［J］.Journal of Harbin Engineering University，2004，25(2):136 －140.

［9］李增刚.Sysnoise Rev 5.6详解［M］.北京:国防工业出版社，2005.

［10］何祚镛.结构振动与声辐射［M］.哈尔滨:哈尔滨工程大学出版社，2001.

［11］张俊杰.基于不同理论的流场中圆柱壳振动能量流和辐射声功率研究［D］.武汉:华中科技大学，2010.