高强度梁类件回弹及补偿的二维截面法修正

聂 昕 申丹凤

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082 2.湖南湖大艾盛汽车技术开发有限公司，长沙，410205

0 引言

汽车钣金件的回弹问题（回弹预测及补偿）一直是汽车行业关注的热点。大量的学者及工程技术人员对此问题进行了分析、研究、探索，并取得了一定的成果。总的来说，对于结构复杂零件的三维回弹量预测和补偿的方法都不够理想，尤其是采用高强度钢板的零件，预测和补偿的效果更差。相比之下，简单形状零件二维回弹量预测和补偿的精度还是比较让人满意的。

1996年，Karafillis等［1］在板件回弹补偿的模具设计中，采用了截面法来计算、判断回弹大小，模具的补偿精度较高。2007年，聂昕等［2］利用二维截面法对汽车梁类件回弹进行了研究，取得了不错的效果。2009年，刘迪辉等［3］利用截面法提出了一种针对任意截面形状的回弹计算理论方法，最后通过某B柱零件证明了其方法的可行性。2011年，吴磊等［4－5］基于截面法对冲压回弹的特征进行了分析并建立了一套评价方法，将回弹模式简化为纯几何运动，并应用优化方法对参数进行了优化，此方法工程实用性强。

但随着高强度钢板在车身上的大量应用，人们发现，高强度钢板的回弹量及变形模式与普通低碳钢零件相比有明显不同，其回弹量远远大于普通低碳钢的回弹量，而且侧壁的卷曲回弹更明显，在成形、切边后容易发生纵向回弹等。因此，利用截面法对高强度梁类件的回弹进行研究出现了新的问题：一是纵向回弹问题，在低碳钢材料梁类件的冲压过程中，零件的纵向方向拉延很充分，发生了比较充分的塑性变形，一般很少会出现纵向回弹，回弹补偿精度也能保证。可是，高强度钢板材料的高强度、低延伸率的特点造成了梁类件往往在纵向也会发生回弹，且数值较大，回弹结果不能忽略。2010年，钱直睿等［6］在研究卡车的纵梁回弹时也发现了此问题，他们通过多次试验及工艺修改确定了回弹量及补偿量并控制回弹量在3mm内。另一个比较严重的问题就是在回弹补偿时，截面法无法正确考虑到零件侧壁补偿后可能出现的负角问题，尤其是在侧壁出现卷曲回弹时，负角问题更为严重。这个问题是现有二维截面法无法解决的，也是上述文献没有考虑到的。Dutton等［7］在2005年对防撞梁进行回弹补偿时提出了避免负角的算法，但同时也提出该算法仅能用于该防撞梁，没有普遍性。Ninshu等［8］提出负角边界的概念，通过负角边界来控制回弹位移的最大比例系数，超过负角边界的比例系数需要重新通过工艺及型面进行修正。2011年，Lee等［9］在预测高级高强度钢回弹时，指出要注意考虑冲压负角对回弹模拟及补偿的影响。

因此，本文针对高强度钢板材料梁类件出现纵向回弹及进行回弹补偿时易出现侧壁冲压负角的问题，对二维截面算法进行修正，主要包括二维截面法的回弹预测和回弹补偿两个方面。以某汽车前纵梁为例，利用修正后的二维截面法对其进行回弹预测及回弹补偿，并对比了算法修正前后结果的差异性。

1 二维截面算法基本思想

二维截面算法是笔者在2007年提出的一种用于汽车梁类件回弹预测及补偿的方法［2］，它是提取梁类零件各典型关键截面，对其截面进行二维回弹计算并根据回弹补偿公式进行回弹节点补偿、循环迭代计算，从而得到满足设计要求的补偿截面的一种优化方法。其基本流程如图1所示。

2 二维截面算法的修正

针对采用高强度钢板材料出现的回弹新问题及二维截面算法的局限性，本文分别对考虑纵向回弹的回弹计算、回弹补偿以及考虑冲压负角的回弹补偿算法进行修正。修正后的算法将根据各个关键截面各节点的回弹值，组合进行节点位移的处理及调整。

图1 二维截面法流程图

2.1 考虑纵向回弹的二维截面法回弹计算

二维截面法只考虑了横向回弹，通过对零件各个横向关键截面的回弹分析，来确定其截面的回弹补偿量，各个截面之间没有关联。零件纵向回弹的出现，就必然要考虑各个截面之间的联系。

根据初始整体回弹结果及零件纵向的复杂程度，选取合适的零件纵向关键截面，一般选取1～3个典型截面。对其纵向截面按照设计工艺进行精确成形、回弹分析，计算出纵向截面各个位置的回弹情况，用于评价零件的纵向回弹水平。将各个位置的Z向回弹情况，根据零件各个横向截面的位置进行插值处理，从而得到各个横向截面的考虑纵向回弹的真实回弹值。

回弹前，截面某点坐标N0＝（X0，Y0，Z0），回弹后，该点坐标为N1＝（X1，Y0，Z1），考虑纵向回弹后，该点坐标为 N1＝（X1，Y0，Z1＋Zri），该点的回弹量为

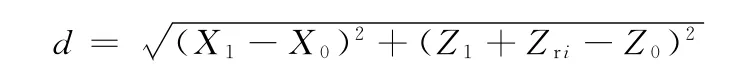
式中，Zri是纵向回弹各个截面上的回弹量。

2.2 考虑纵向回弹的二维截面法回弹补偿

在对零件各个关键截面进行二维回弹分析后，需要对其进行回弹补偿来解决零件的回弹问题。对比截面内回弹前后节点的回弹值，根据二维截面回弹补偿算法来对截面上的节点进行回弹补偿。

未修正前的二维截面法节点回弹补偿公式为

S1集：节点 N2＝ （（2 X0－X1），Y0，Z0）

S2集：节点 N2＝ （（2 X0－X1），Y0，2Z0－Z1）

其中，S1集包含顶面和两侧面的节点；而S2集主要包含底面翻边和侧面底圆角上的节点。

由于高强度钢零件存在不可忽略的纵向回弹Zr，原有的补偿算法得不出准确的补偿值，所以必须利用纵向回弹Zr来对各截面的回弹补偿算法进行修正。

算法修正后，S1的节点N2＝（（2 X0－X1），Y0，Z0－KZri）；而S2的回弹补偿后的节点坐标为N2＝（（2 X0－X1），Y0，2Z0－Z1－KZri）。其中，K 是比例系数，K 值一般小于或者等于1。

经过大量回弹算例的实践，发现了一个现象，随着板件材料抗拉强度的升高，尤其是新型超高强度钢板的应用后，通过节点偏置补偿算法补偿节点的距离往往不够，需要较多次的迭代，反复补偿才行，比较费时费力，所以，根据实践积累的大量数据，在偏置算法上又增加了两个参数，进一步优化完善了节点偏置算法。

设I为材料系数，I＝f（t，σb）代表了材料系数与板厚t和材料抗拉强度σb两个变量的一个函数关系，0.8≤I≤2.2，其中t0＝1.2mm，σb0＝270MPa，即t0、σb0为适用于此节点偏置算法的普通板材的一般标准。设J为整体能动控制系数，一般为0.9≤J≤1.3。所以，最终修正后回弹补偿算法为S1集：节点 N2＝J（I（2 X0－X1），Y0，Z0－KZri）；S2集：节 点 N2＝J（I（2 X0－X1），Y0，2Z0－Z1－KZri）。

2.3 考虑冲压负角的二维截面法回弹补偿

当零件出现较大回弹，尤其材料采用的是超高强度钢板时，在回弹补偿时，要特别注意板件侧壁补偿的负角问题。

梁类件侧壁的拔模角度数不大，一般都小于10°。如果回弹量较大，而零件的拔模倾角又不够大，就可能出现补偿后的型面出现负角问题，这样的型面模具是无法进行冲压、调试的。一般希望补偿侧壁后的倾角要至少大于β，1°＜β＜3°。这样的拔模角度才有利于成形。

所以，如果发现型面补偿后倾角小于β的情况，就必须重新调整。

按照回弹类型的不同，修正负角的补偿算法分为两种情况：

第一种是发生截面角度回弹，尤其是侧面发生角度回弹时，即侧面形状没有发生变化，只是侧面与冲压方向的角度发生了变化。在这种状态下，补偿后的侧壁节点坐标和成品节点坐标保持一致，法兰边的节点沿用原算法求得新坐标（修正负角算法1）。 其中，侧壁节点：N2＝（X0，Y0，Z0）； 法 兰 边 节 点：N2＝J（I（2 X0－ X1），Y0，2Z0－Z1）。回弹前截面某点坐标N0＝（X0，Y0，Z0）；回弹后该点坐标为 N1＝（X1，Y0，Z1），具体见图2所示。

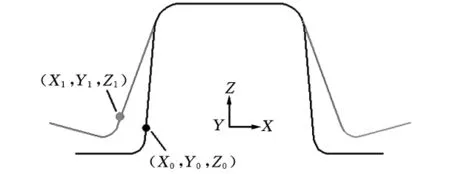
图2 梁类件截面示意图

在回弹补偿后，对截面节点进行曲线拟合时，法兰边拟和的曲线和侧壁拟和的曲线按照零件圆角值光顺连接即可。由于对截面进行了负角修正，修正后肯定在长度上和成品有偏差，一般都偏小。所以，为了保证截面线的长度相等，一定要对修正后的补偿截面线进行调整。

这种修正方法较简单，原因是角度回弹相对于卷曲回弹和扭曲回弹变形更加规则，形状更好控制。在存在基本补偿的情况下，只需调节凸模圆角和利用整形工序即可控制，所以，只需要保证把法兰边补偿到位即可。侧壁的补偿可以通过侧整形解决。

第二种情况是出现卷曲回弹的时候。这种情况一般出现在DP钢和TRIP钢这种高级或者超高强度钢板零件。这时候用上述修正补偿算法效果不好，因为侧壁出现了卷曲，如果侧壁还是保持不变的话，永远无法补正卷曲情况。所以，第二种修正补偿算法（修正负角算法2）是：

考虑整个域为搜索区间，设侧壁上补偿后紧邻的两节点为 An（Xn，Zn），An＋1（Xn＋1，Zn＋1），如果∂＝arctan＞β，最终An＋1坐标为（Xn＋1，Zn＋1）；如果∂＝arctan≤β，最终An＋1坐标为（Xn＋dsinβ，Zn＋dcosβ）。其中d＝

法兰边上的节点保持不变，侧壁和法兰边之间的过渡节点需要用大圆角插值来实现。在构造B样条曲线时，用大圆角对圆角处节点进行拟和，保持其光顺性。

3 考虑纵向回弹及冲压负角的拼焊板纵梁回弹计算及补偿

以一个典型案例来反映考虑纵向回弹及冲压负角的二维截面法的应用。此零件是某车型的前纵梁后段加强板，采用激光拼焊板冲压而成。材料分别为CR780DP和CR340LA，板厚为1.75mm和2.0mm，属于新型高强度钢板。材料特性如表1所示。零件及工艺补充面见图3。该纵梁的成型工序包括：拉延，修边，翻边整形，冲孔－侧冲孔。

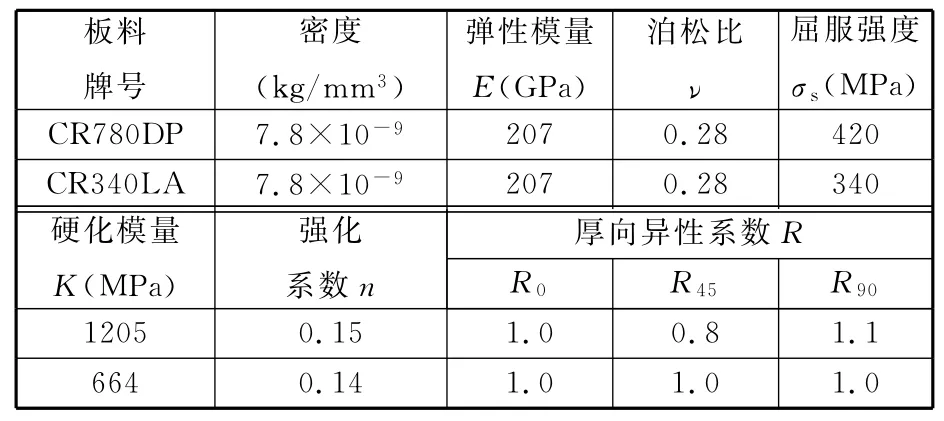
表1 拼焊板的材料性能参数

图3 拼焊板纵梁零件及工艺补充面

3.1 拼焊板纵梁的二维截面回弹计算

该零件整体形状比较单一，为典型梁类件，应用二维截面法进行分析如下。首先进行整体回弹计算，了解变形趋势、确定外部参数及关键截面。此纵梁的成形工序包括：拉延，修边，翻边整形，冲孔－侧冲孔。其中，拉延工序（OP10）的压边力为784kN，翻边整形工序（OP30）的压边力为117.6kN。

从图4整体回弹云图上可以看出，纵梁两端都有上跳的回弹现象，而且回弹量比较大，在3～5mm之间，1号点的回弹量为4.34mm。2号点的回弹量为3.00mm。而法兰边的最大回弹量达到了9mm。这说明该高强度钢纵梁不仅法兰边回弹量大，而且由于未发生充分的塑性变形，造成两端部上跳回弹。这就要求除了选取横向截面计算横向回弹外，一定需要对零件纵向做二维截面的回弹分析来确定零件的纵向回弹量。

图4 零件修边后的整体回弹图

为了保证精度，选取20个横向截面和3个纵向截面作为分析截面，然后利用二维截面法借助有限元软件LS－DYNA进行成形、回弹计算。如图5所示。

图6、图7列出了最大回弹截面X＝－267mm处的回弹云图和截面位置回弹图。

图5 零件选取的关键二维截面

从图中可以看出，截面右侧最大回弹位移为10.9mm，左侧最大回弹位移为8.7mm，基本上属于角度回弹。位置回弹图展示了截面回弹值和截面位置的关系。其他截面回弹值见表2。

图6 截面X＝－267mm处的回弹云图

图7 截面X＝－267mm处的回弹图

表2 各截面数值计算回弹值

图8为Y＝0处的纵向截面回弹图，截面的两端明显发生变形，产生比较大的回弹。计算值比整体预测值要大一些，但整体趋势保持一致。纵向截面回弹的最大值为6.36mm，出现在材料为CR340LA的这部分零件的端头（即图8云图的最右端），在纵向方向坐标X＝278mm的位置，回弹基本消失，回弹量几乎为零。而材料为CR780DP的这一部分拼焊零件从左边端头到纵向方向坐标X＝－579mm的位置，回弹量基本一致；然后从纵向方向坐标X＝－579mm到X＝－254mm位置，回弹量基本按线形下降直到0；中间一段基本上没有回弹，最大值才0.2mm。所以，在回弹截面节点偏置后，根据纵向截面的回弹值，需要对各截面的Z向位置进行整体调节。根据工程问题的精密要求，可以进行函数拟合来简化计算。

图8 Y＝0处的纵向截面回弹图

通过横向及纵向各截面的回弹分析，可以得到该零件的回弹情况，横向回弹的最大值为10.9mm，纵向回弹的最大值为6.36mm。两端端头上跳比较严重。实际试模板件回弹结果见图9。从图9可以看到，板件两端的确有比较大的Z向回弹，经测量最大回弹值有7.5mm，和截面法计算出来的回弹值比较接近。最大的回弹发生在X＝－245mm左右的区域，回弹值为12mm。

图9 实际冲压板件的回弹

3.2 拼焊板纵梁的二维截面回弹补偿

根据各典型截面的回弹计算值可以发现，该零件的两端存在较大的纵向回弹，中部的纵向回弹不大，但侧壁尤其是法兰边的回弹较大，最大回弹量在10mm以上，存在回弹补偿时出现冲压负角的危险。下面选择典型截面来说明二维截面算法的修正。

3.2.1 考虑纵向回弹的二维截面修正

根据零件各纵向截面和横向截面的回弹分析结果，对其截面节点进行回弹补偿。其中修正后的回弹补偿算法为

S1集：节点N2＝J（I（2 X0－X1），Y0，Z0－KZri）。

S2集：节点 N2＝J（I（2 X0－X1），Y0，2Z0－Z1－KZri）。

其中拼焊板中材料为CR780的截面材料补偿系数I取1.42，材料为CR340的截面材料补偿系数I取1.20。而且对各截面回弹补偿的大小可以通过能动系数J根据实际经验进行能动地控制，本例20个截面的系数J取值在0.9～1.2之间。取截面X＝－588mm处回弹状况来对比整个补偿算法修正前后的不同。图10显示了该截面在回弹前、回弹后，以及算法修正前的补偿后、算法修正后的补偿后四种状态。

图10 X＝－588mm截面的补偿算法修正前后的对比图

从图10可以看出，考虑了纵向回弹的状态和没考虑纵向回弹的状态差了很多。最后修改的型面和原补偿型面也有了很大的变化，尤其在两端部。

3.2.2 考虑冲压负角的二维截面修正

在此纵梁上取X＝－213mm处一截面，此处的回弹比较大，最大值为8mm。而侧面拔模角度比较小，左侧为6°，右侧为5°。左侧壁经过回弹补偿后，发现拔模倾角几乎为0。这样不满足要求，需要进行修正。经过测量，左侧回弹基本上能算作纯粹回弹或者直回弹。所以利用修正负角算法1就可以解决。而从右侧壁的回弹可以看出，经过补偿后，右侧壁的拔模倾角出现了负角，而且由于零件造型的原因，右侧壁在1／3处有条棱线，在成形过程中起到了一个卡子的作用。所以棱线上回弹较少，几乎没有，但棱线下出现了卷曲回弹。这就必须要求应用修正负角算法2来对侧壁进行修正。修正后的对比图如图11所示。

图11 修正补偿算法前后截面的对比

从图11可以看出，左侧壁的直回弹补偿，修正前后区别较大，主要是在侧壁的角度上，但是底面的法兰边补偿会起到牵制作用，再进行成形、回弹迭代计算时，回弹量会减小很多，而且，将很少发生回弹的转化。

而右侧壁的卷曲回弹，通过修正负角算法2得出的补偿截面线的拔模角定为2°。由于侧壁存在卷曲回弹，按照修正算法1的补偿得出的补偿线无法解决这个问题，因为其没有考虑侧壁卷曲变形问题。为了保证补偿后的截面长度和回弹后的截面长度一致，人为在法兰边上补偿长度差值，具体见图12所示。

图12 修正补偿算法前后截面的局部放大

3.2.3 修正后的截面及型面生成

图13为全部截面通过修正补偿算法补偿后的补偿情况和与回弹前后的对比图。通过补偿因子修正后，会较容易得到满意的补偿面，根据补偿后型面和原有压料面做OP10拉延工序的工艺补充，再进行成形和回弹的模拟，2～3次的循环补偿就可以得到比较满意的结果，迭代过程一般不会超过4次，少许的回弹偏差在后续整形工序可以解决。

图13 所有回弹截面的补偿图

本算例通过三次的循环迭代，最大公差控制在－0.3～0.3mm以内，满足补偿要求。图14是循环迭代后最终生成的纵梁补偿型面。从图14可以看出，考虑了纵向回弹及冲压负角的回弹补偿型面能满足冲压成形工艺要求。

4 实验验证

图14 最终生成的纵梁补偿型面

将补偿后的零件型面进行数控加工来制造模具，模具经过少许调试，冲压出来的零件放在检具上检查，表面质量好，零件和检具的间隙比较均匀，型面偏差都在公差要求范围之内。图15为前纵梁经过三次补偿修改后放在检具上的成品图。可以看到，零件在检具上安放平稳，间隙均匀。

图15 前纵梁三次补偿修改后放检具上的成品图

5 结论

（1）通过考虑纵向截面的回弹，并引入材料系数、能动控制系数修正了回弹计算、补偿算法。通过考虑回弹补偿后出现的侧壁负角，针对侧壁回弹变形模式的不同（直回弹和卷曲回弹），分别采用两个不同补偿算法公式处理、修正了原有补偿算法。

（2）实践证明，修正后的二维截面补偿算法解决了原有算法回弹补偿后忽视纵向回弹及会出现冲压负角的可能性，一般通过3次循环迭代计算即可解决实际回弹问题，有较好的可行性及较高的精度，能广泛地应用于汽车各种梁类件。

（3）由于有限元软件计算回弹值精度不够高，现在无法将此方法应用于形状变化复杂的三维零件，但这是以后重点研究的方向。

［1]Karafillis A P，Boyce M C.Tooling and Binder Design for Sheet Metal Forming Processes Compensating Springback Error［J］.International Journal of Machine Tools Manufacture，1996，36（4）：503－526.

［2]聂昕，成艾国，钟志华，等.二维截面法在精确预测汽车梁类件回弹上的应用［J］.汽车工程，2007，29（1）：83－86.Nie Xin，Cheng Aiguo，Zhong Zhihua，et al.Application to Predict Springback Accurately in Automotive Side Member by 2－D Section Method［J］.Automotive Engineering，2007，29（1）：83－86.

［3]刘迪辉，吴磊，李光耀，等.任意截面线回弹理论计算方法及应用［J］.锻压技术，2009，34（6）：143－147.Liu Dihui，Wu Lei，Li Guangyao，et al.Theoretical Calculation Method and Its Application of Arbitrary Section Springback［J］.Forging ＆ Stamping Technology，2009，34（6）：143－147.

［4]吴磊，李光耀，曹昭展.基于截面法的冲压回弹特征评价方法［J］.中国机械工程，2009，20（19）：2280－2283.Wu Lei，Li Guangyao，Cao Zhaozhan.Method for Determining Parameters of Springback Based on Characteristic Sections［J］.China Mechanical Engineering，2009，20（19）：2280－2283.

［5]吴磊，曹昭展，李光耀.一种弧形高强钢车身零件冲压回 弹 控制方法 ［J］.计算 力 学 学 报，2011，28（1）：37－43.Wu Lei，Cao Zhaozhan，Li Guangyao.A New Method of Control of Springback of High Strength Steel Parts with Arched Surface［J］.Chinese Journal of Computational Mechanics，2011，28（1）：37－43.

［6]钱直睿，刘克欣，辛显静，等.卡车纵梁弯曲回弹分析与补偿研究［J］.模具工业，2010，36（6）：36－39.Qian Zhirui，Liu Kexin，Xin Xianjing，et al.Springback Analysis of Bent Truck Longeron and Compensation Study［J］.Mould Industry，2010，36（6）：36－39.

［7]Dutton T，Edwards R，Blowey A.Tool Design for a High Strength Steel Side Impact Beam with Springback Compensation［C］／／5th European LS－DYNA Users’Conference.Birmingham，England，2005：6－10.

［8]Ninshu M，Yasuyoshi U，Yuko W.Springback Prediction by Yoshida－Uemori Model and Compensation of Tool Surface Using JSTAMP［J］.Numisheet，2008，9：473－478.

［9]Lee M G，Kim C，Pavlina E J，et al.Advances in Sheet Forming－ materials Modeling，Numerical Simulation，and Press Technologies［J］.Journal of Manufacturing Science and Engineering，2011，133（6）：1001－1012.