基于粒子群优化神经网络的机器人精度补偿方法研究

周 炜 廖文和 田 威 万世明 刘 勇

1.南京航空航天大学，南京，2100162.中航工业成都飞机工业（集团）有限责任公司，成都，610091

0 引言

在飞机的制造过程中用工业机器人进行自动柔性装配、部件加工（如钻铆、喷漆、焊接等），可以极大地提高飞机生产的效率和质量的可靠性［1］。当以机器人为载体配合一定的末端执行装置进行自动制孔时，由于飞机装配过程中制孔的工作量很大，因此示教编程无法满足生产高效率的要求，所以通常只能通过离线编程指定机器人末端执行装置的TCP（tool center point）的理论位姿来控制机器人进行定位。然而由于机器人零部件的加工制造误差、机器人的安装误差、传动机构误差、机器人负载以及环境等因素的影响，机器人实际到达的位姿与理论位姿之间存在着一定的偏差。机器人的精度是反映机器人性能的一个重要指标，它包括绝对定位精度和重复定位精度。一般工业机器人有着较高的重复定位精度，但它的绝对定位精度却是比较低的，往往重复定位精度达到0.1mm的机器人，其绝对定位精度误差却可能有1～3mm。而采用离线编程控制机器人进行定位所产生的误差是由机器人的绝对定位精度来决定的，因此为了提高制孔的精度和质量，就必须对提高机器人绝对定位精度的补偿方法进行研究。

在已有的文献中，提高机器人绝对定位精度的补偿方法按照控制方式通常可以分为两种：一种是全闭环控制。这种方法在系统中增加了末端实时反馈检测，通常是通过视觉识别技术或是采用嵌入式控制方法，把激光跟踪仪、机器人、上位机集成起来对机器人末端的位姿进行实时快速地反馈，从而提高机器人的定位精度。采用这种控制方式一般可以达到±0.1mm的绝对定位精度，但是对于那些外形比较复杂的部件以及在工业现场中，此方法不易实施。另一种是半闭环的控制方式，即不在系统中引入实时末端反馈检测，只是通过标定的方法来提高机器人的绝对定位精度。此种控制方式相关的研究方法主要有以下几种［2］：运动学模型参数标定法［3－7］、基于神经网络的正标定 法［8］、基于神经网络的逆标定法［9－10］。这些方法补偿后的精度通常可以达到±1mm，可以满足焊接等对精度要求不是很高的应用场合，但不适应飞机装配这种对精度有着很高要求的场合。

针对上述问题，本文在机器人空间网格精度补偿方法的基础上，进一步综合考虑了环境温度的变化对机器人绝对定位精度的影响。此时除了已经考虑到的影响定位精度的三个空间坐标因素外，还增加了温度这一影响因素，由于这四个影响因素之间有着无数种组合，因而通过实验来采集空间网格精度补偿方法中所需要的空间网格顶点的实际定位数据就不太现实。BP神经网络又称为误差反向传播（back propagation）神经网络，具有实现任何复杂非线性映射的能力。针对BP神经网络的这个特点，本文提出了基于神经网络的机器人综合精度补偿方法。同时为了防止神经网络在训练过程中陷入局部极值，利用粒子群优化方法对它的初始值进行了优化。

1 机器人空间网格精度补偿方法

机器人空间网格精度补偿方法的基本思想是假设机器人在一定边长的立方体网格区域内，任一点的绝对定位精度与包含它的立方体网格的八个顶点的绝对定位精度具有一致性或存在某种内在关联［11］。因此对于工作空间内的任一点可以通过它所在的立方体网格的八个顶点的绝对定位误差进行空间插值，估算出该点的绝对定位误差，并将它逆补偿到理论坐标上从而提高它的绝对定位精度。

反距离加权法是常用的空间插值方法［12－13］，它是一种加权平均算法，以两点之间的距离的倒数作为权值，即距离越近相互影响的权值因子越大，距离越远相互影响的权值因子就越小。当已知点分布比较均匀时，插值点的逼近程度也比较高，且计算简单，运算速度快。

将机器人的工作空间按一定的步长均匀地进行空间网格划分，划分的任一立方体网格如图1所示，其中立方体网格八个顶点Ki（i＝1，2，…，8）理论定位坐标为（Xi，Yi，Zi），通过激光跟踪仪测得的实际定位坐标为（X′i，Y′i，Z′i），将它们进行比较得到相应的绝对定位误差为（ΔXi，ΔYi，ΔZi）。

图1 空间网格精度补偿原理图

立方体网格中的任一点P（X，Y，Z）的绝对定位误差可以通过以下几个步骤预测出：

（1）计算立方体网格各顶点对P点的影响权值。首先根据P点的理论坐标计算它与立方体网格各顶点实际定位坐标的距离di，接着根据距离的远近反向求得权值qi，其中

（2）插值计算P点的误差。根据立方体网格各顶点对P点的影响权值大小在机器人坐标系各方向上分别进行加权平均，插值计算出P点在坐标系三个方向上的误差ΔX、ΔY、ΔZ，表示为

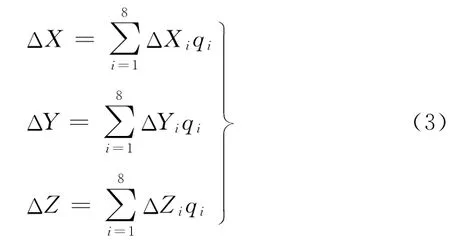
（3）用预测出的P点绝对定位误差对它的理论坐标进行修正，用修正后的坐标（X′，Y′，Z′）驱动机器人进行定位：

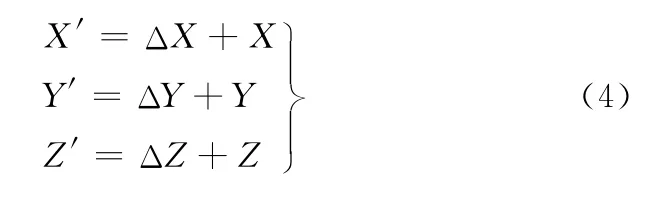
2 基于粒子群优化神经网络的综合精度补偿模型

采用机器人空间网格精度补偿方法，在机器人负载确定的情况下，需要测量在其工作空间内划分的立方体网格的各个顶点的绝对定位误差，继而才能通过空间插值的方法对工作空间内的每个点进行精度补偿，此时并没有考虑环境温度发生变化带来的影响。因此当机器人标定时的温度与实际加工时的温度相差较大时，由于机器人在两个不同温度下运行相同的指令到达相同点时的定位精度可能会发生变化，此时如果仍然采用标定的数据来补偿和定位，机器人的定位精度将得不到保证。而引入温度影响因素后，尽管划分网格的顶点数量是有限的，然而由于温度是个连续变化的变量，所以理论上不能通过实验的方式来获得在任意温度条件下所划分的网格的各个顶点对应的绝对定位误差。神经网络通过训练样本可以模拟某种客观存在的内在规律，因此可以考虑在负载恒定、温度发生变化的情形下利用神经网络模拟机器人定位的内在规律。

由此，为综合利用机器人空间网格精度补偿方法和BP神经网络方法各自的优点，将它们结合起来作为综合的精度补偿方法。其基本思想是：在标定时选取任意几个温度下划分的空间网格顶点的理论坐标和对应的实际定位数据分别作为输入输出样本来训练神经网络，以模拟机器人在不同温度下的定位规律，应用时则用检测的实时环境温度结合包围目标定位点最小网格的顶点的理论定位坐标作为神经网络的输入来预测相应的实际定位坐标，最后再利用空间网格精度补偿方法对该点进行精度补偿。图2所示为神经网络的输入输出示意图。其中，（X，Y，Z）为划分的立方体网格的某个顶点的理论定位坐标，T为检测到的现场温度，（X′，Y′，Z′）为神经网络预测出的在当前温度下该顶点的实际定位坐标。当工作温度与标定温度一致时，神经网络的预测作用就相当于一个查表过程。

图2 神经网络输入输出示意图

相关理论已经证明神经网络的初始权值和阈值的选择会对网络最终的训练效果产生重要影响。图3是PSO优化BP神经网络算法的流程图，它包括BP神经网络和PSO优化算法两部分，其中PSO优化算法部分的目的是给已确定网络结构的BP神经网络提供最优的初始权值和阈值以防止网络在训练过程中陷入局部极小值。在获得优化的初始权值和阈值后，神经网络以实验获得样本数据进行训练，直至满足结束条件为止。

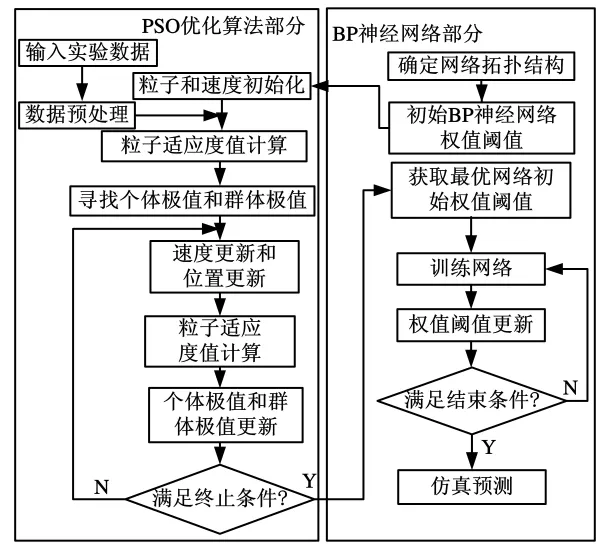
图3 PSO优化BP神经网络算法流程

当神经网络经过训练满足精度要求后就可以结合机器人空间网格精度补偿方法对位于机器人工作空间内的任一点的绝对定位精度进行补偿了。综合精度补偿方法流程如图4所示。

图4 综合精度补偿方法流程图

3 实验验证

提出的基于粒子群优化神经网络的机器人精度补偿方法在本实验室的KUKA公司生产的六自由度KR150－2型串联机器人上进行，额定负载为1500N，测量工具是FARO SI型激光跟踪仪。

实验现场如图5所示，在标定过程中，对划分的网格点进行定位时，机器人都是从相同姿态的同一个出发点也称为HOME点开始的，且所有定位点的目标姿态也是相同的。温度的调节控制是通过一个额定功率为3836W（5P）的空调来进行的，且每次调节温度后的测量工作都是在调温约8h后室温基本处于稳定的状态下进行的。

图5 实验现场

3.1 测量数据的获取

由于需要用激光跟踪仪对所有划分的立方体网格顶点的实际定位数据进行测量，所以这就涉及到大量的坐标系之间的转换，坐标系转换关系如图6所示。文献［14－15］介绍了机器人加工系统各坐标系建立的方法，这里不再进一步叙述。下面假设激光跟踪仪测量坐标系与机器人坐标系、世界坐标系、工具坐标系已经建立关联。为了便于测量，将靶标球放置在末端制孔机构的压力脚处时的球心位置作为TCP。在建立了坐标系间关联后，在负载恒定的情况下，以300mm步长对位于机器人零点位置正前方工作空间的一块1.5m×0.9m×0.3m的区域进行立方体网格划分，如图6所示，共划分了15个立方体网格，涉及48个网格顶点。接着分别在19℃、23℃、26℃、29℃这四个温度条件下对划分的立方体网格的所有顶点进行定位实验，共得到480组实验数据。从图中很容易看出其中有些网格顶点是重合的，因此对这些重复的网格顶点的实际定位数据取平均值作为最终的实际定位数据，这样做可以在一定程度上减少测量误差带来的影响。

图6 坐标系转换关系

3.2 PSO优化BP神经网络的确定

在获得了实验数据后，需要建立对应的神经网络模型。通过反复试验，最终确定BP神经网络由四层组成，分别为输入层、隐含层1、隐含层2、输出层，其中输入层包含4个节点，2个隐含层都各自包含7个节点，输出层包含3个节点。网络的训练函数为“trainlm”，它采用Levenberg－Marquardt算法；网络的学习率为0.1；网络训练的样本数为187；验证的样本数为5。确定PSO优化算法的种群数为50，进化的次数为600，其他的相关的参数设置如表1所示。

表1 BP神经网络和PSO优化算法重要参数设置表

用设置的相关参数以及试验取得的192组样本值输入到MATLAB编制的程序中进行训练，结果如图7所示，随机选取的5组测试样本在X、Y、Z方向上的预测精度都在0.06mm以下，满足精度要求。此外，对于用于网络训练的187组样本值，绝大多数点的训练精度在0.1mm以下，对于极个别超过0.1mm的点，究其原因是因为这些点处于划分网格的边缘，样本中缺少足够描述它们特征的信息。而三个方向上综合误差的数值大小与机器人标称的重复定位精度0.15mm数值相仿。

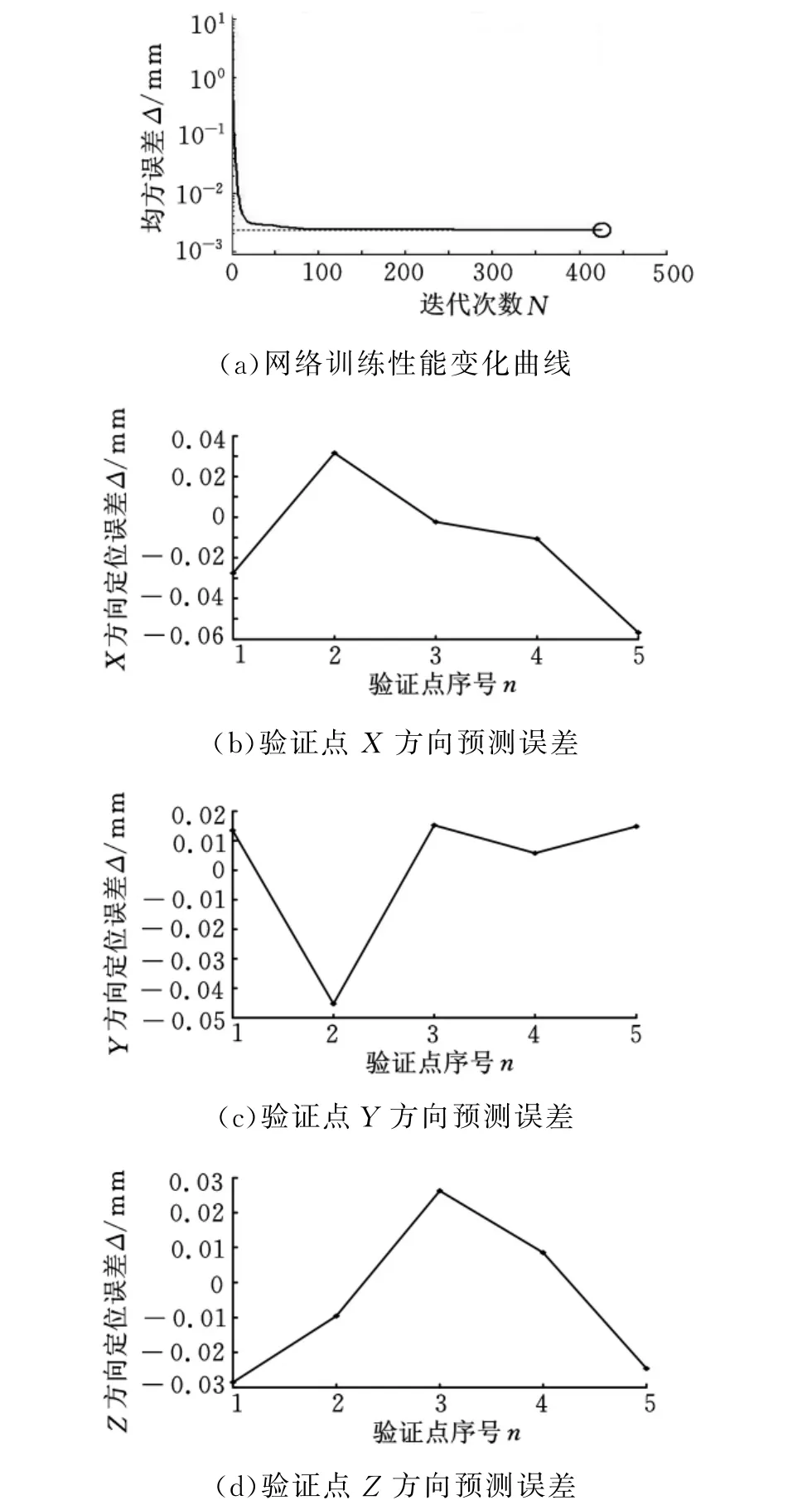
图7 神经网络训练结果

为了验证提出的基于粒子群优化神经网络的机器人精度补偿方法在工作温度与标定温度不一致的情况下的适应性，在划分的待加工区域里任意选取5个测试定位点，其期望坐标值及测试温度如表2所示。

调节环境温度使温度发生改变，用表2中坐标值结合温度作为神经网络的输入，用预测出的所处立方体网格八个顶点的实际定位坐标进行空间网格精度补偿，然后用修正后的坐标值控制机器人进行定位，经激光跟踪仪测量得到实际定位坐标，用它与期望坐标相比较，结果如表3所示，经过补偿后这些测试点的最大定位误差是0.32mm，最小误差是0.11mm，平均误差是0.19mm。

表2 测试点位置及环境温度

表3 测试点精度补偿效果 mm

4 结语

在机器人空间网格精度补偿方法的基础上进一步考虑环境温度因素给机器人的绝对定位精度带来的影响，提出了基于粒子群优化神经网络的机器人精度补偿方法。实验结果显示测试点的绝对定位精度最高为0.11mm，最低为0.32mm，比未补偿前的1～3mm有了一个数量级的提高，因此提出的精度补偿方法可以在标定温度与实际工作温度不一致的条件下有效地提高机器人的绝对定位精度，证明了该方法在理论上和技术上均是可行的。

［1]许国康.大型飞机自动化装配技术［J］.航空学报，2008，29（3）：734－740.Xu Guokang.Automatic Assembly Technology for Large Aircraft［J］.Acta Aeronautica et Astronautica Sinica，2008，29（3）：734－740.

［2]龚振邦.机器人机械设计［M］.北京：电子工业出版社，1995.Gong Zhenbang.Robot Mechanical Design［M］.Beijing：Publishing House of Electronics Industry，1995.

［3]任永杰，邾继贵，杨学友，等.利用激光跟踪仪对机器人进行标定的方法［J］.机械工程学报，2007，43（9）：195－200.Ren Yongjie，Zhu Jigui，Yang Xueyou，et al.Method of Robot Calibration Based on Laser Tracker［J］.Chinese Journal of Mechanical Engineering，2007，43（9）：195－200.

［4]焦国泰，阿德依科拉夫，余跃庆.工业机器人位姿误差的计算［J］.机械科学与技术，2002，21（1）：35－39.Jiao Guotai，Egorov，Yu Yueqing.A Method for Calculating Position and Orientation Errors of Industrial Robot［J］.Mechanical Science and Technology，2002，21（1）：35－39.

［5]解则晓，辛少辉，李绪勇，等.基于单目视觉的机器人标定方法［J］.机械工程学报，2011，47（5）：35－39.Xie Zexiao，Xin Shaohui，Li Xuyong，et al.Method of Robot Calibration Based on Monocular Vision［J］.Journal of Mechanical Engineering，2011，47（5）：35－39.

［6]Judd R P，Knasindki A B.A Technique to Calibrate Industrial Robots with Experimental Verification［J］.IEEE Transaction on Robotics and Automation，1990，6（1）：20－30.

［7]蔡鹤皋，张超群，吴伟国.机器人实际几何参数识别与仿真［J］.中国机械工程，1998，9（10）：11－14.Cai Hegao，Zhang Chaoqun，Wu Weiguo.The Robot Actual Geometry Parameter Identification and Simulation［J］.China Mechanical Engineering，1998，9（10）：11－14.

［8]Xu W L，Wurst K H，Watanabe T，et al.Calibration a Modular Robotic Joint Using Neural Network Approach［C］／／Proceedings of IEEE International Conference on Neural Networks.NewYork：IEEE，1994：2720－2725.

［9]Zhong X L，Lewis J M，Rea H.Neuro－Accuracy Compensator for Industrial Robots［C］／／Proceedings of IEEE International Conference on Neural Networks.NewYork：IEEE，1994：2797－2802.

［10]夏凯，陈崇端，洪涛，等.补偿机器人定位误差的神经网络［J］.机器人，1995，17（3）：171－176.Xia Kai，Chen Chongduan，Hong Tao，et al.A Neural Network Model for Compensating Robot Kinematics Error［J］.Robot，1995，17（3）：171－176.

［11]周炜，廖文和，田威，等.面向飞机自动化装配的机器人空间网格精度补偿方法研究［J］.中国机械工程，2012，23（19）：2306－2311.Zhou Wei，Liao Wenhe，Tian Wei，et al.Robot Accuracy Compensation Method of Spatial Grid for Aircraft Automatic Assembly［J］.China Mechanical Engineering，2012，23（19）：2306－2311.

［12]朱求安，张万昌，余钧辉.基于GIS的空间插值方法研究［J］.江西师范大学学报，2003，28（2）：183－188.Zhu Qiuan，Zhang Wanchang，Yu Junhui.The Spatial Interpolations in GIS［J］.Journal of Jiangxi Normal University，2003，28（2）：183－188.

［13]林忠辉，莫兴国，李宏轩，等.中国陆地区域气象要素的空间插值［J］.地理学报，2002，57（1）：47－56.Lin Zhonghui，Mo Xingguo，Li Hongxuan，et al.Comparison of Three Spatial Interpolation Methods for Climate Variables in China［J］.Acta Geographica Sinica，2002，57（1）：47－56.

［14]曲巍崴，董辉跃，柯映林.机器人辅助飞机装配制孔中位姿精度补偿技术［J］.航空学报，2011，32（10）：1951－1960.Qu Weiwei，Dong Huiyue，Ke Yinglin.Pose Accuracy Compensation Technology in Robot－aided Aircraft Assembly Drilling Process［J］.Acta Aeronautica et Astronautica Sinica，2011，32（10）：1951－1960.

［15]张文增，陈强，孙振国，等.弧焊机器人工件坐标系快速标定方法［J］.焊接学报，2005，26（7）：1－4.Zhang Wenzeng，Chen Qiang，Sun Zhenguo，et al.Quick Calibration Method of Part Coordinates for Arc Welding Robot［J］.Transactions of the China Welding Institution，2005，26（7）：1－4.