大型风机叶片模态参数识别的试验研究
张磊安 黄雪梅
山东理工大学,淄博,255049
0 引言
模态参数在结构动态设计中起着至关重要的作用,也是识别结构系统其他参数的先决条件。阻尼作为一个主要的模态参数,反映了构件在振动中能量耗散的能力。目前对构件进行模态参数识别主要采用试验模态方法,因为它针对构件本身进行,所以试验数据更加可信。自由悬臂梁在工程领域应用比较广泛,静力学、动力学的理论与试验领域涌现了许多研究成果[1-4],许多重要的成果可被直接参考,因此本文将研究对象(风力机叶片)等效为一个根部固定的自由悬臂梁进行模态参数识别。另外,在叶片的模态参数识别方面也有一些重要研究成果,如文献[5]采用有限元方法对叶片的模态参数进行数值计算,并将其与实际测试值进行比较,检验了有限元模型的正确性;文献[6]剖析了有限元分析中阻尼矩阵的构建方法,解决了具有单独共振频率或具有临近共振频率的振动问题。
本文采用试验方法对风机叶片的模态参数(阻尼和频率)进行识别。首先从理论角度推导了悬臂梁自由衰减振动的阻尼比识别关系式。为了完成风机叶片的大振幅自由衰减试验,构建了一套大型风机叶片自由衰减试验系统,对aeroblade3.6-56.4风机叶片进行了自由衰减试验,并通过阻尼比识别关系式和傅里叶变换得出了该叶片的模态参数。
1 阻尼比关系式推导
对叶片的振动响应信号进行分析,可得出反映该叶片的阻尼、振幅衰减率和低阶固有频率等一系列模态参数。其中,阻尼反映叶片在运动过程中受阻力影响,能量逐渐衰减导致运动减弱的特性。在自由衰减过程中,叶片振幅以指数形式衰减,不同阻尼比ξ下的振动衰减曲线如图1所示。

图1 自由衰减曲线
由图1可知,阻尼比ξ越大,振幅衰减地越快。若0<ξ<1,则称为欠阻尼运动,该状态下的自由衰减响应可表示为

式中,A、φ分别为初始幅值和相位;ωn为无阻尼固有频率;ωd为有阻尼固有频率。
设相邻振动周期T的前后时间点分别为t1和t2,同时由于ξ足够小,故由式(1)可得
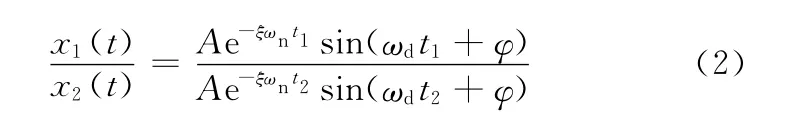
根据t2=t1+T,T=2π/ωd得
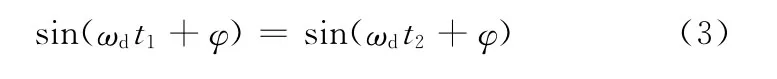
相邻两个周期的振动幅值之比称为衰减系数,表示为
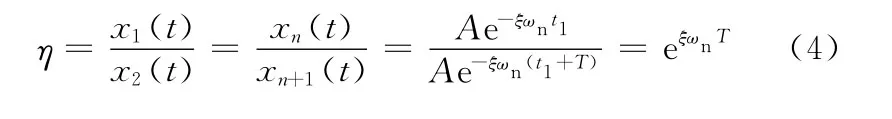
自由振动过程中,相距n个振动周期的衰减系数可表示为
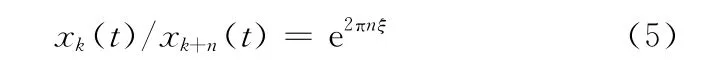
式中,xk(t)、xk+n(t)为相邻n个周期的振幅。
根据式(5),阻尼比ξ可表示为

即根据相距n个周期的振幅,可求出叶片阻尼比。
2 试验方案
为了得到叶片的模态参数,进行了自由衰减试验,具体试验方案如下:叶片根部通过若干个高强度螺栓固定在筒型加载基座上,加载支架固定在地面导轨上,加载支架内部安装液压加载系统,液压绞车通过钢丝绳将叶片加载点拉到设定挠度后,通过快卸装置迅速释放加载力,实现叶片的自由衰减振动。叶片另一侧位置固定一个激光测距仪,实现对叶片振幅的实时测量,反馈后的数据通过RS485总线传给PLC,PLC将数据处理之后送到上位机界面存储和显示。同时叶片尖部安装一个加速度计,实时测试叶片的加速度,并反馈给控制器。总体试验方案如图2所示。

图2 大型风机叶片自由衰减试验方案
3 模态参数识别试验
3.1 试验对象
被试验的叶片型号为aeroblade3.6-56.4[7],该叶片额定功率为3.6MW,长 度 为56.4m,质量为17 277kg,重心距离叶片根部19.05m,如图3所示。限于篇幅,本文仅测试该叶片最小挥舞方向(Min flapwise)的阻尼。

图3 aerobalde3.6-56.4风机叶片
3.2 自由衰减试验
将风机叶片通过法兰螺栓固定在筒型加载支座上,在沿叶片展向70%处固定好夹具,将快卸装置串联于钢丝绳之中,激光测距仪发出的激光点打在叶片表面。液压绞车通过钢丝绳将叶片加载点拉到设定挠度后,快卸装置迅速释放加载力,完成叶片的自由衰减运动,试验现场如图4所示。

图4 风机叶片自由衰减试验
风机叶片做大振幅自由衰减振动时的抖动非常大,因此对叶片振幅的测量不宜采用接触式传感器。本文选用激光测距仪,数据转换时间小于40ms,相比叶片的振动周期,数据采集的实时性完全满足要求。测量系统及试验环境如表1所示。

表1 测试系统技术指标
3.3 阻尼比识别
对aeroblade3.6-56.4风机叶片做不同初始振幅下的自由衰减试验。限于篇幅,仅给出初始幅值为0.5m和1.0m时,沿叶片展向70%处的振幅衰减曲线,如图5所示。
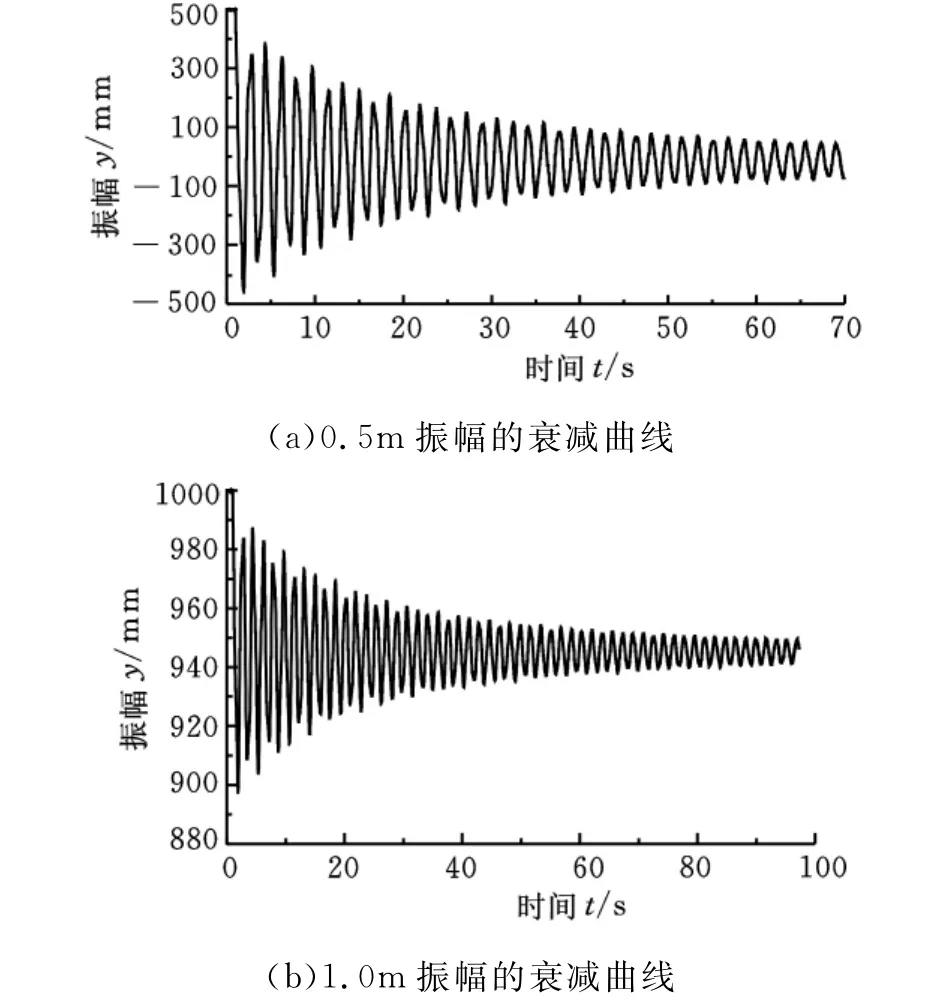
图5 aeroblade3.6-56.4振幅自由衰减曲线
根据振幅曲线可得,在叶片衰减过程中,它的各阶模态产生了叠加,导致加载点振幅并不是恒定地呈递减状态,具体表现为振幅在不断波动。根据阻尼比计算关系式(式(6))和叶片振幅衰减试验曲线,同时采用样条曲线拟合,得到叶片阻尼比与初始振幅的关系,如图6所示。
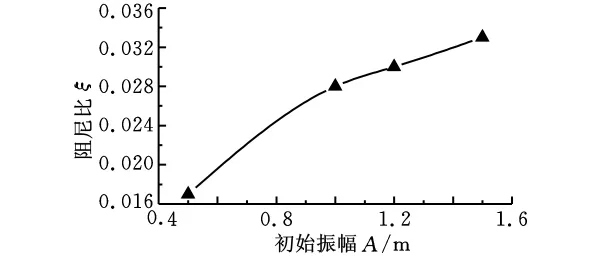
图6 叶片阻尼比随振幅变化曲线
从图6可以看出,初始振幅越大,阻尼比也相应变大,基本呈非线性变化。例如,当起始振幅为1.0m时,阻尼比ξ=0.028。
3.4 低阶固有频率识别
将数据采集仪得到的加速度信号进行快速傅里叶变换,所得频谱如图7(部分截图)所示。aeroblade3.6-56.4风机叶片最小面向的低阶固有频率:min flapwise1st=0.57Hz,min flapwise2nd=1.67Hz。
4 结论
(1)推导的阻尼比识别关系式能较好地计算大型风机叶片的阻尼比。
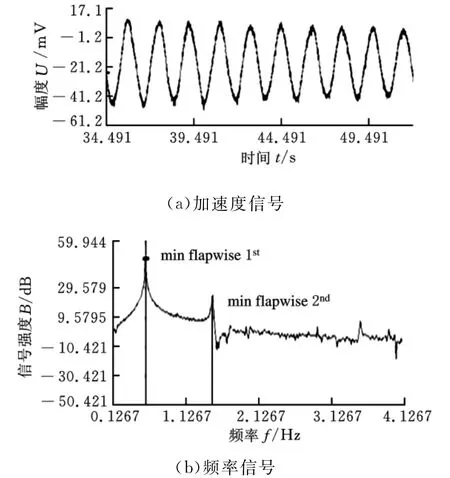
图7 aeroblade3.6-56.4风机叶片频谱图
(2)构建的大型风机叶片模态参数识别平台,可以进行系列化大型风机叶片的阻尼比和低阶固有频率的识别试验,试验结果可为后续的风机叶片疲劳加载试验打下基础。
(3)自由衰减过程中,叶片振幅逐渐衰减,模态叠加使得振幅呈不规则的波动。阻尼比与叶片的初始振幅有较大关系,初始振幅越大,阻尼比相对越大,且呈非线性正比关系。
(4)由于叶片振动曲线中含有高阶振动分量,下一步可通过滤波等信号处理手段得到各阶模态下叶片的振动衰减曲线,进而研究不同模态下叶片的阻尼特性。
[1]胡明勇,王安稳.自由阻尼悬臂梁瞬态响应的近似解析解[J].华中科技大学学报(自然科学版),2009,37(11):108-110.Hu Mingyong,Wan Anwen.Approximate Analytical Solutions to the Transient Response of Unconstrained Damped Cantilever Beams[J].Journal of Huazhong University of Science and Technology,2009,37(11):108-110.
[2]李家文,李道奎,周建平.冲击波作用下的悬臂梁瞬态响应的传递函数方法[J].振动与冲击,2007,26(3):101-114.Li Jiawen,Li Daokui,Zhou Jianping.Transient Response Analysis of a Cantilever Beam under Blast Wave with Distributed Transfer Function Method[J].Journal of Vibration and Shock,2007,26(3):101-103.
[3]吴国荣.一种求解梁动力响应的新方法[J].振动与冲击,2006,25(4):146-148.Wu Guorong.A New Method for Solving Dynamic Response of Beams[J].Journal of Vibration and Shock,2006,25(4):146-148.
[4]Viola E,Ricci P,Aliabadi M H.Free Vibration Analysis of Axially Loaded Cracked Timoshenko Beam Structures Using the Dynamic Stiffness Method[J].International Journal of Sound and Vibration,2007,38(3):124-153.
[5]李声艳,徐玉秀,周晓梅.风力发电机风轮动态特性分析[J].天津工业大学学报,2006,25(6):65-67.Li Shengyan,Xu Yuxiu,Zhou Xiaomei.Analysis of Dynamic Characteristic for Wind Turbine Rotor[J].Journal of Tianjin Polytechnic University,2006,25(6):65-67.
[6]王春健,陈官峰,卿华.涡轮叶片模态实测阻尼比的有限元应用[J].航空动力学报,2012,27(2):260-264.Wang Chunjian,Chen Guanfeng,Qing Gua.Application of Damping Ratio for Turbine Blades by Modal Testingon Finite Element Anlysis[J].Journal of Aerospace Power,2012,27(2):260-264.
[7]张磊安,乌建中,陈州全,等.兆瓦级风机叶片静力加载控制系统设计及试验[J].中国机械工程,2011,22(18):2182-2185.Zhang Leian,Wu Jianzhong,Chen Zhouquan,et al.Design and Trial of MW Wind Turbine Blade Static Loading Control System[J].China Mechanical Engineering,2011,22(18):2182-2185.

