基于改进EMD的旋转机械耦合故障诊断方法研究
时培明 李 庚 韩东颖
燕山大学,秦皇岛,066004
0 引言
目前,国内外学者对裂纹和碰摩单一故障研究较多,提出了一些有效方法来诊断裂纹故障和碰摩故障[1-4]。但在实际转子系统中,常常出现裂纹故障和碰摩故障共存的情况。这种耦合故障转子的动力学行为较单一故障转子更加复杂,且故障相互影响,不容易诊断。针对这一问题,文献[5]采用有限元方法分析了裂纹碰摩耦合故障转子系统的响应,在显著碰摩故障信号中诊断出了裂纹故障。文献[6]建立了带有裂纹碰摩耦合故障且具有三轴承支承的双跨弹性转子系统动力学模型,利用延拓打靶法和Floquet理论研究其稳定性。文献[7]提出了一种基于微分的经验模态分解方法,并在转子裂纹碰摩耦合故障诊断中取得了良好的效果。虽然,针对耦合故障的诊断开展了一些研究,但是在诊断精度和准确性上还有待提高。
耦合故障信号具有典型的非线性和非平稳性,对于这类信号,普通的信号分析方法具有局限性。EMD是近年来发展起来的处理非平稳、非线性信号的时频分析方法[8]。该方法克服了传统时频分析方法中的不足,并在机械故障诊断领域得到了广泛应用[9-13]。
本文提出一种基于相似极值延拓法[14]和余弦窗函数的改进EMD方法,并将其应用在转子-轴承系统裂纹碰摩耦合故障诊断中。采用本文方法对耦合故障仿真信号进行特征提取时,边界谱和希尔伯特谱既包含裂纹引起的高频信号成分,又包含碰摩引起的低频信号成分。由此诊断出该故障系统中同时存在裂纹和碰摩故障,从而验证了该方法的有效性。
1 系统力学模型和运动微分方程
图1所示为建立的含有裂纹碰摩耦合故障的对称刚性支承转子-轴承系统模型[15]。模型两端对称结构的滑动轴承支承中间的转子,转子与轴承之间为无质量的弹性轴。转子左侧有一弓形横向裂纹,其深度为a。转子受到碰摩故障影响,其碰摩函数为P。图1中,O1为轴瓦几何中心,O2为转子几何中心,O3为转子质心,kc为定子刚度,k为弹性轴刚度,m1为转子在轴承处的集中质量,m2为转子处的等效集中质量。左侧滑动轴承产生的非线性油膜力在水平和垂直方向上的分力分别为Fx、Fy。

图1 裂纹碰摩转子-轴承系统模型
设转子左端的径向位移为x1、y1,转子圆盘的径向位移为x2、y2,则具有裂纹碰摩耦合故障的转子-轴承系统运动微分方程为

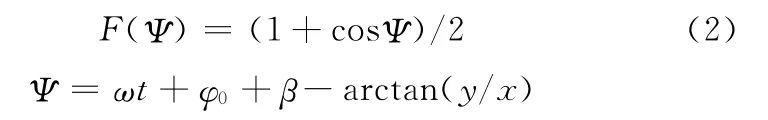
式中,u为转子的偏心量;c1为转子在轴承处的阻尼系数;c2为转子圆盘的阻尼系数;ω为转子转速;g为重力加速;ε、δ为仅与裂纹深度a有关的相对刚度参数;F(Ψ)为裂纹开闭函数,本文采用余弦波模型来表示裂纹开闭过程;φ0为初相位;β为裂纹方向与偏心之间的夹角,(x,y)为转子初始位置,如图2所示。

图2 裂纹截面模型
相对刚度系数ε、δ的表达式为

转子、定子碰摩函数P(e≥ξ)为
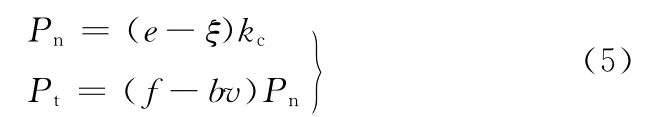
式中,Pn为法向碰摩力;Pt为切向摩擦力;ξ为静止时转子与定子之间的间隙;e为转子轴心位移;f为不考虑速度影响时的摩擦因数;b为速度影响系数;v为转子静件间的相对滑动速度。
e>ξ时,系统发生碰摩故障,如图3所示。
碰撞发生(e≥ξ)时,转子正向碰摩力与切向摩擦力分解在XY坐标系可以表示为


图3 碰摩力模型
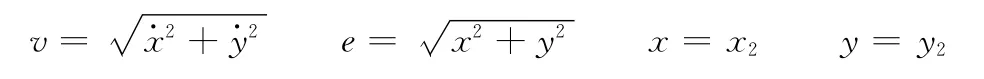
式(1)中油膜力沿X和Y两个方向的分量为

式中,μ为润滑油黏度;c为轴承径向间隙;R为轴承半径;L为轴承长度。
2 EMD改进方法
HHT(Hilbert-Huang transform)先通过EMD将待分析的信号分解为一系列不同尺度的本征模式函数(intrinsic mode function,IMF)信号,再针对这些IMF分量信号进行希尔伯特变换,得到希尔伯特谱。IMF信号一般满足两个条件:①从全局特性上看,极值点数必须和零点数一致或者至多相差一个;②在某个局部点,极大值包络和极小值包络在该点的算术平均值是零,即两条包络线关于时间轴对称。
我们可以把任何信号x(t)按下面步骤分解:
(1)用三次样条线将所有的局部极大值点连接起来形成上包络线。
(2)用三次样条线将所有的局部极小值点连接起来形成下包络线。
(3)上下包络线的平均值记为m1,求出

理想地,如果h1是1个IMF,那么h1就是x(t)的第1个分量。
(4)如果h1不满足IMF的条件,把h1作为原始据,重复步骤(1)~步骤(3),得到上下包络线的平均值m11,再判断h11=h1-m11是否满足IMF的条件,如不满足,重复循环k次,得到h1k=h1(k-1)-m1k,使得h1k满足IMF条件。记c1=h1k,则c1为信号x(t)的第1个满足IMF条件的分量。
(5)将c1从x(t)中分离出来,得到

将r1作为原始数据重复以上过程,得到x(t)的第2个满足IMF条件的分量c2,重复循环n次,得到n个满足IMF条件的分量。这样就有

当rn成为一个单调函数不能再从中提取满足IMF条件的分量时,循环结束。这样由式(9)和(10)得到

对式(11)中的每个内禀模态函数ci(t)作希尔伯特变换得到
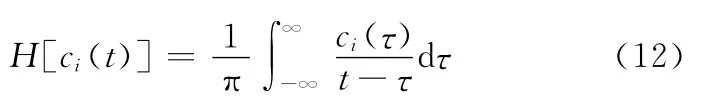
构造解析信号

于是得到幅值函数

和相位函数

进一步可以求出瞬时频率:

这样,原始信号就可以表示为
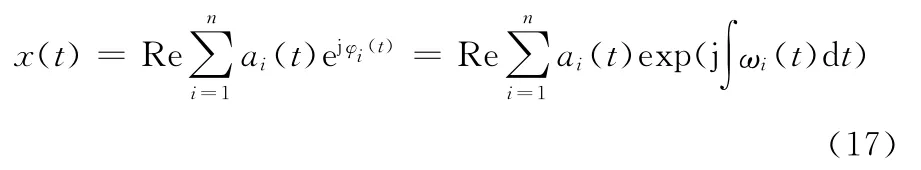
相似极值延拓加余弦窗函数法是改进端点效应,提高EMD准确性的新方法。该方法先对原信号进行相似极值延拓处理,然后加上余弦窗函数,最后再按照原函数的长度去掉延拓部分,这样可以得到更准确的IMF。相似极值延拓方法的原理如下。
设离散信号:

式中,n为离散数据点数;Δt为采样步长。
X(t)有M个极大值和N个极小值,它们对应的时 间 为tmax(M)和tmin(N),函 数 值 为xmax(M)和xmin(N)。下面以左侧延拓为例进行算法说明:

若延拓时遇到tmin(0)>0或tmax(0)>0的情况,需要继续延拓出tmin(-1)或tmax(-1),方法如下:

然后在拟合时只用tmin(-1)、tmax(0)、t1或tmax(-1)、tmin(0)、t1,不再用tmin(0)或tmax(0)。在给延拓出的点赋值时,若遇到xmin(0)>x(t1),可令xmin(0)=xmin(1);若xmax(0)<x(t1),可令xmax(0)=xmax(1)。
定义余弦窗函数:

式中,L为信号延拓后的长度;S信号两端延拓中较长的延拓长度。
用余弦函数窗w(t)对信号x(t)进行处理,即将信号与窗函数进行内积运算,得到信号y(t)= 〈x(t),w(t)〉:
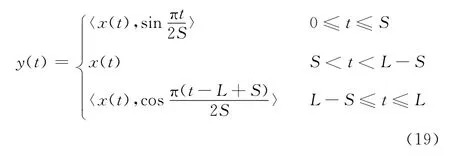
对处理后的信号y(t)进行EMD分解,再将分解得出的每个IMF分量的两端按照延拓前数据的长度去掉相应的延拓部分。最后对减去延拓部分的IMF进行边界谱和希尔伯特谱分析。
3 数值仿真和故障诊断
用EMD方法对故障进行诊断,需要得到故障信号的时域图。由式(1)可以看出,含有裂纹碰摩耦合故障的转子系统是一个有复杂外激励的非线性系统。目前,分析这种系统的最有效的方法就是数值仿真,本文用目前最常用的变步长4阶龙格-库塔法对式(1)进行数值求解,系统参数选取如下:m1=4kg,m2=32.5kg,R=25mm,L=12mm,c=0.11mm,a=15mm,μ=0.018Pa·s,c1=1050N·s/m,c2=2100N·s/m,f=0.1,b=0.01,k=25MN/m,kc=45MN/m,u=0.05mm,ω=789.3rad/s,ξ=0.5mm,φ0=β=0。
通过数值仿真得到振动信号时域图,图4a为转子左端的径向位移x1的时域图,图4b为转子圆盘的径向位移x2的时域图。由图4可以看出,由于碰摩和裂纹故障的影响,x1和x2的振动有很强的非线性。采用改进的EMD方法对两组数据进行处理,并通过边界谱和希尔伯特谱进行故障诊断。

图4 x1和x2的时域图
首先对上述两图进行延拓加窗处理,再用EMD方法分解得到两组IMF,如图5所示。由于EMD方法本身原因产生虚假模态,故只给出IMF1~IMF4。

图5 x1和x2的EMD处理结果
为了得到裂纹碰摩耦合故障的故障特征,需要对已经得到的IMF求边界谱图。首先求得转子左端径向位移x1的边界谱,如图6a所示,并通过与单一故障的边界谱图比较来分析故障特征,如图6b、图6c所示。这里的单一故障边界谱是由耦合故障模型简化得到的,由于篇幅所限不进行详细说明。

图6 x1边界谱
为了更好地看出倍频关系,图6、图7横轴采用频率比,即信号振动频率与转子旋转频率之比。由图6a可以看出,x1处的故障信号除1倍频外还有2倍频等高频存在。通过与图6b的比较发现,高倍频是由裂纹故障引起的,由此可以诊断出故障信号含有裂纹故障信号特征,即该系统存在裂纹故障。但由于耦合作用,低频碰摩故障信号特征则不明显,下面要对x2的振动信号进行分析。
图7a表明,该信号同时含有低频成分(1/3倍频)和高频成分(5/2倍频、7/2倍频)。由图7可知,低频成分是由碰摩故障引起的,裂纹故障是系统产生高频信号的原因,由此诊断出该系统存在裂纹碰摩耦合故障。
希尔伯特谱能够更清晰地显示出信号所含故障特征。图8表明,x1的信号中包含1倍频、2倍频和3倍频成分,x2的信号既含有3倍频又含有1/3倍频。由此可以更好地诊断出该系统同时存在裂纹和碰摩故障。
4 结语

图7 x2边界谱
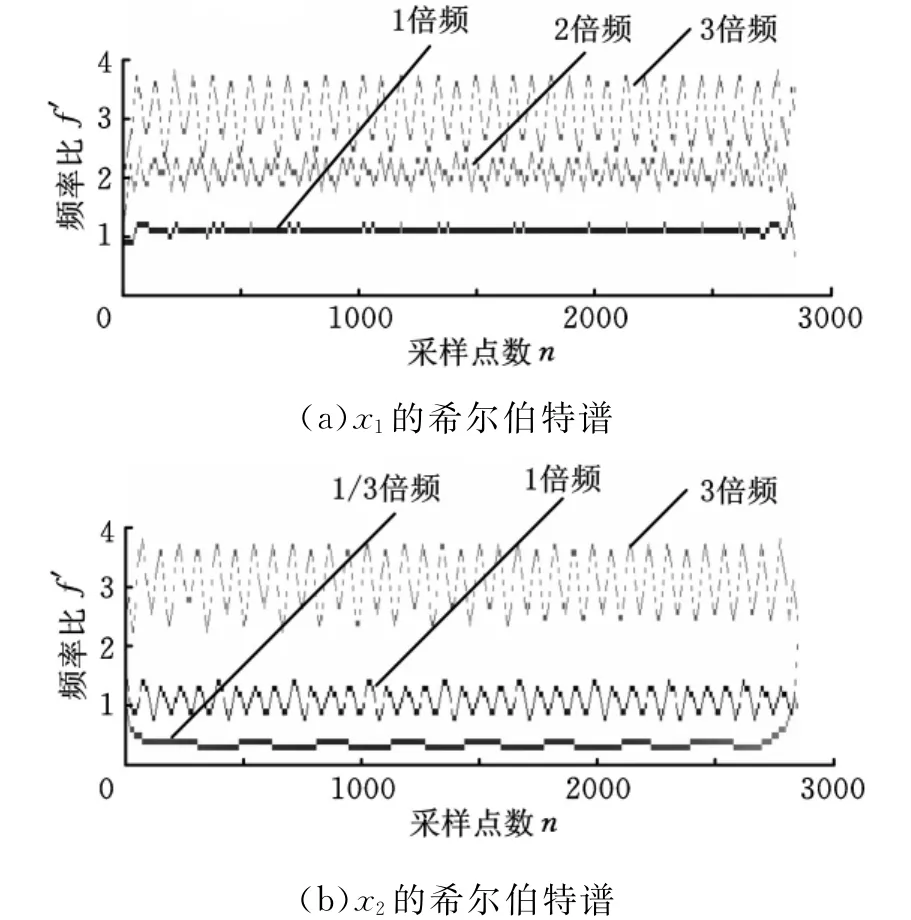
图8 x1和x2的希尔伯特谱
对信号做延拓加窗处理是一种抑制EMD中端点效应的新方法。先利用相似极值延拓方法对信号两端进行延拓,再根据延拓情况对信号用余弦窗函数加以处理,得到更准确的IMF。把该方法应用到裂纹碰摩转子-轴承系统模型的故障诊断中,通过对系统转子左端的振动信号和转子圆盘处振动信号的分析,准确诊断出该信号同时存在由裂纹引起的高频信号和碰摩引起的低频信号,证明了改进EMD能够对旋转机械耦合故障进行有效诊断。
[1]Gounaris C D,Papadopoulos C A.Crack Identification in Rotating Shafts by Coupled Response Measurements[J].Engineering Fracture Mechanics,2002,69(3):339-352.
[2]Hu N Q,Wen X S.The Application of Duffing Oscillator in Characteristic Signal Detection of Early Fault[J].Journal of Sound and Vibration,2003,268(5):917-931.
[3]Sekhar A S,Mohanty A R,Prabhakar R.Vibrations of Cracked Rotor System:Transverse Crack versus Slant Crack[J].Journal of Sound and Vibration,2005,279(3/5):1203-1217.
[4]王翔,王仲生.基于改进Hilbert-Huang变换的转子碰摩故障诊断[J].中国机械工程,2011,22(24):2937-2940.Wang Xiang,Wang Zhongsheng.Incipient Rubimpact Fault Diagnosis of Rotor System Using Improved HHT[J].China Mechanical Engineering,2011,22(24):2937-2940.
[5]姚红良,李鹤,李小彭,等.裂纹碰摩耦合故障转子系统诊断分析[J].振动工程学报,2006,19(3):307-212.Yao Hongliang,Li He,Li Xiaopeng,et al.Diagnoses of Coupling Fault of Crack and Rub-impact in Rotor Systems[J].Journal of Vibration Engineering,2006,19(3):307-212.
[6]罗跃纲,闻邦椿.双跨转子-轴承系统裂纹-碰摩耦合故障的稳定性[J].机械工程学报,2008,44(4):123-132.LuoYuegang,Wen Bangchun.Stability of the Two-span Rotor-bearing System Periodic with Coupling Faults of Crack and Rub-impact[J].Chinese Journal of Mechanical Engineering,2008,44(4):123-132.
[7]景蓓蓓,李鸿光.基于微分的经验模式方法在转子裂纹和碰摩故障诊断中的应用[J].噪声与振动控制,2009(5):66-69.Jing Beibei,Li Hongguang.Fault Diagnoses of Cracked Rotor and Rub-impact Rotor Based on DEMD Method[J].Noise and Vibration Control,2009(5):66-69.
[8]Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proceedings of the Royal Society London A,1998,454(1971):903-995.
[9]Yang Yu,He Yigang,Chen Junsheng,et al.A Gear Fault Diagnosis Using Hilbert Spectrum Based on MODWPT and a Comparison with EMD Approach[J].Measurement,2009,42(4):542-511.
[10]Li Yujun,Tse P W,Yang Xin,et al.EMD-based Fault Diagnosis for Abnormal Clearance between Contacting Components in a Diesel Engine[J].Mechanical Systems and Signal Processing,2010,24(1):193-210.
[11]程军圣,于德介,杨宇.EMD方法在转子局部碰摩故障诊断中的应用[J].振动、测试与诊断,2006,26(1):24-27.Cheng Junsheng,Yu Dejie,Yang Yu.Application of EMD to Local Rub-impact Fault Diagnosis in Rotor Systems[J].Journal of Vibration,Measurement & Diagnosis,2006,26(1):24-27.
[12]戴桂平,刘彬.EMD相关度去噪及其在轧机信号处理中的应用[J].电子器件,2009,32(1):191-194.Dai Guiping,Liu Bin.Research on EMD Denoising Method Based on the Correlation Degree and Its Use in the Signal Processing for Rolling Mill’s Signal[J].Chinese Journal of Electron Devices,2009,32(1):191-194.
[13]吴虎生,吕建新,吴庐山,等.基于EMD和SVM的柴油机气阀机构故障诊断[J].中国机械工程,2010,21(22):2710-2714.Wu Husheng,LüJianxin,Wu Lushan,et al.Fault Diagnosis for Diesel Valve Train Based on SVM and EMD[J].China Mechanical Engineering,2010,21(22):2710-2714.
[14]沈路,周晓军,张志刚,等.Hilbert-Huang变换中的一种端点延拓方法[J].振动与冲击,2009,28(8):168-174.Shen Lu,Zhou Xiaojun,Zhang Zhigang,et al.Boundary-extension Method in Hilbert-Huang Transform[J].Journal of Vibration and Shock,2009,28(8):168-174.
[15]罗跃纲,张松鹤,闻邦椿.转子-轴承系统裂纹-碰摩耦合故障的非线性特性研究[J].振动与冲击,2005,24(3):43-46.Luo Yuegang,Zhang Songhe,Wen Bangchun.Study on Nonlinear Characteristics of Rotor-bearing System with Coupling Faults of Crack and Rub-impact[J].Journal of Vibration and Shock,2005,24(3):43-46.

