异形内孔曲面的磨料流均匀加工方法研究
张克华 许永超 丁金福 陆 爽 程光明
浙江师范大学,金华,321004
0 引言
磨料流加工是一种利用含磨粒的半流动状态磨料流,在一定压力下强迫其流经被加工表面,由磨粒的刮削作用去除工件表面材料,从而达到光整加工目的的工艺方法[1]。该加工法在曲面精密加工方面已取得了许多成功的经验[2]。磨料流加工参数和磨料介质的流变特性是影响加工效果的两个重要因素,介质黏度和工作压力对金属去除率和表面粗糙度有显著的影响[3-6]。不规则的异形曲面加工中,磨料流道的不一致导致各部分所受的剪切应力不同,导致表面各部分加工质量的一致性比较差。王阿成等[7]分析了磨粒流加工时链条片状型腔表面的剪切应力分布,通过置入模芯方法改善加工过程中的剪切应力分布,并取得一定的效果。但总体而言,目前对异形曲面均匀化加工尚缺乏系统性研究。
磨料流加工中加工效果的预测通常采用曲面所受剪切应力对抛光效果的影响,并借助数学模型和有限元方法进行预测、设计和评估[8-12]。因此,笔者利用非牛顿流体模型来模拟加工过程中磨料的流动情况,利用设置模芯的方法实现均匀化加工,从仿真结果出发去设计能使加工表面剪切应力趋向相同的磨料流加工流道,从而使复杂孔洞表面精度的一致性达到理想目标。
1 理论分析、仿真分析及加工实验
1.1 理论基础
磨料流加工时,磨粒的分布是随机的,每个磨粒在加工过程中的运动状态很难进行准确描述,所以从微观机理的角度去理解磨料流的加工过程非常困难[13-14]。磨料流是由高分子载体、磨粒和添加剂均匀地混合而成的一种黏弹性流体,磨粒多为SiC、Al2O3、B4C和金刚石粉等。磨料流内聚力强,具有弹性,并且与金属的黏着力小,表现为一种弱黏性的非牛顿流体[15]。因此,从宏观角度可将磨料流的运动看作是一种非牛顿流体流动,利用非牛顿流体模型可以对磨料介质的运动状态进行简单有效的描述。由高分子材料的性质可知,磨料流黏度会随着剪切速率的增大而减小,因此在CFD仿真过程中考虑“剪切变稀”的因素。本文利用非牛顿流体的幂律方程描述磨料流的工作状态:

式中,τ为剪切应力,Pa;η为黏度,Pa·s;∂γ/∂t为剪切速率,s-1;n为流动指数。
令非牛顿流体的表观黏度为

则幂律方程(式(1))可写成

在给定温度和压力下,非牛顿流体的ηa不是常数,它与剪切速率∂γ/∂t有关。
1.2 磨料介质
实验所用的磨料是由高分子聚合物材料、硅胶稀释剂和相应的磨粒按一定的比例配制而成的。磨粒一般根据工件的材质来决定,铝合金的研磨抛光一般采用白刚玉,经过淬火处理的较硬材料需要选用SiC等较硬的磨料。SiC又称金刚砂,硬度高,热传导性好,适用于加工硬度较高的材料。调制而成的磨粒流必须具有良好的黏弹性和可塑性,并与金属的黏着力小,表现为一种典型的高黏度非牛顿流体。磨料的性能参数如表1所示。磨料介质的黏度与其剪切率之间的关系曲线如图1所示。

表1 磨料介质的性能参数
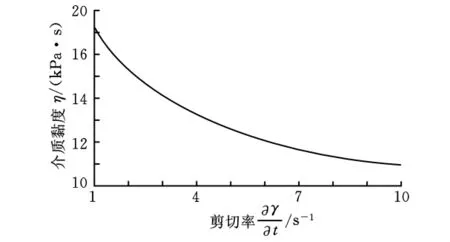
图1 磨料介质黏度与剪切率的关系曲线
1.3 实验工件
为了验证仿真结果,选择摆线形状异形孔洞曲面工件作为加工对象。工件的高度为60mm,其几何参数如图2所示,当磨料介质流经较窄的区域时,加工表面所受到的剪切应力较大;当流经空间较大的区域时,加工表面所受到的剪切应力相对较小。异形曲面所形成加工流道的不规则性,使得磨料流加工中各个曲面所受到的剪切力不均,从而难以达到较为一致的表面精度。实验中,表面状态的主要测试部位如图2中的1、2、3位置。

图2 摆线形状异形孔洞曲面的几何尺寸
1.4 仿真分析
利用非牛顿流体模型,通过COMSOL Multiphysics软件中的CFD模块来模拟放入不同模芯时磨料介质在摆线形状孔洞内的流动状态,并分析磨料介质速度、剪切率及剪切应力的分布。通过设计和制造不同的模芯对CFD仿真结果进行验证。实际加工中,磨料流的工作压力设为1.3MPa,磨料介质的密度初始值为1841.8kg/m3,结合表1中介质的性能参数进行建模仿真。将磨料介质流速、剪切率及剪切应力作为判断摆线形状孔洞加工表面质量一致性的检测依据。
首先对磨料流在无模芯异形曲面内的流动状况进行分析。工件中部橫截面上,磨料介质的流速分布如图3所示。磨料流的流速在径向上急剧减小,其主要原因是磨料流在纵向截面上异形表面各点至流道中心的距离不同,导致各截面间的剪切速率不同,从而导致剪切应力不一致。由此不难发现,在往复加工过程中,不同的剪切应力对工件表面进行抛光的效果不尽相同,往往导致被加工表面精度不一致。
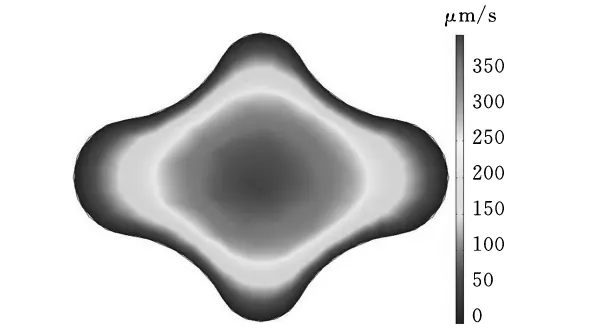
图3 无模芯加工过程中的速度分布
磨料介质在流动过程中的剪切率分布如图4所示。在磨料流加工过程中,磨料流往复加工时受力的情况基本一致,但方向相反。因此,只需考虑流道平行方向上剪切速率为正值的半个周期的情况。如图4所示,在相对较窄的区域,工件表面所受到的剪切速率较大。结合剪切应力与剪切速率之间的关系(式(1))可知,在相对较窄的观察部位(图2中2处)将受到相对较大的剪切应力,而在其他部位(图2中1处和3处)的剪切应力相对较小且几乎相等。在这种情况下,各个部位所受到的不同剪切应力将在工件内壁表面形成不同的加工效果。

图4 无模芯加工过程中的剪切速率分布
然后,对在加工工件内置入2个圆柱体后的流动状况进行分析。工件中部的磨料流流速和剪切速率分布分别如图5、图6所示。

图5 置入圆柱体模芯时的速度分布
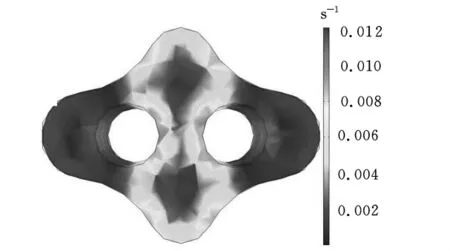
图6 置入圆柱体模芯时的剪切速率分布
由图5可知,磨料流在1处和2处的部分区域内的流速基本相同,但2个圆柱体之间和2个圆柱体与部位3之间的流速依然很大。这表明在加工过程中,这部分区域的磨料流量要比其他区域的磨料流量大。加工过程中磨料的剪切速率分布如图7所示。部位3所受到的剪切速率比部位1、部位2所受到的剪切速率大,这是由部位3磨料流较大的流量造成的。因此,部位3要比其他区域受到更大的剪切应力。置入2个圆柱体后,工件内壁各个部分所受到剪切速率的最大差值减小,由约0.1130s-1降为约0.0347s-1,剪切速率的差值也得到相应的减小。
仿真得出,由于孔洞曲面的不规则性,磨料流流速、剪切率及剪切应力在工件内壁上呈不均匀分布,较窄部位受到的剪切应力大,较宽部位受到的剪切应力小。通过改变曲面各部位介质的流速,可以改变剪切应力的分布,从而改变加工效果。
为了使曲面各部位介质的流速基本相同,设计了与工件内壁形状相似的模芯。图7、图8所示分别为工件中部的磨料介质的流速和剪切速率分布情况。结果表明,利用等宽度的流道有利于改善剪切速率的分布,使各曲面所受的剪切应力趋向一致。3处的流速虽有微量的偏大,但其偏离量已是一个非常小的值(最大的速度差值约为4.7138μm/s)。由图8可知,工件内壁各部位的剪切速率分布较为均匀。由于3处存在着相对较大的弯曲度(致使磨料流在此处的剪切速率比其他部位的剪切速率要大),但其偏离量也已经非常小了(最大的剪切速率差值约为8.93×10-3s-1)。在这种情形下,磨料流可以在整个加工表面形成较为均匀的剪切应力,从而使工件内壁得到精度一致的表面。
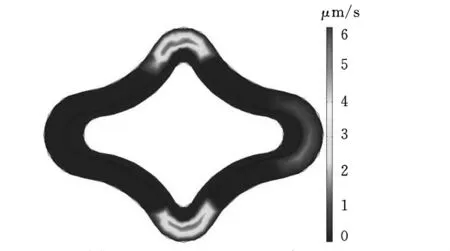
图7 置入相似模芯时的速度分布

图8 置入相似模芯时的剪切速率分布
1.5 加工实验
为了提高异形内孔曲面加工精度的一致性,设计了一种合适的模芯,以使异形曲面获得较为一致的表面加工精度。通过设置不同的模芯对异形曲面工件进行加工实验,以验证仿真结果的正确性。实验使用的仪器设备为自主开发的单柱形磨料流抛光机AFD-100、JB-4C精密粗糙度测试仪等仪器设备。
整个模芯装置由上压盖、下压盖和模芯组成。模芯通过螺栓固定在压盖后,再与夹具组合形成磨料流动通道。采用两种不同类型的模芯进行对比实验:①置入2个半径均为3mm的圆柱体模芯(柱状模芯与左右摆线之间的距离为5mm),如图9所示;②与工件内壁形状相似的模芯,其与内壁间的距离均为2mm,如图10所示。

图9 圆柱体模芯

图10 与工件内壁相似的模芯
2 结果分析
2.1 无模芯时的工件内壁
磨料流加工后,图2中1、2、3处的表面粗糙度Ra如图11所示,加工表面的粗糙度随着加工循环次数的增加而减小。磨料流加工后,在2处得到了相对较小的表面粗糙度。在受到几乎相同的剪切应力下,1处和3处得到了相近的表面粗糙度。由于1处和3处所受到的剪切应力相对较小,其表面粗糙度Ra比2处的大。所得到的表面粗糙度Ra的结果与流道平行方向上剪切应力的分布情况非常的相似。因此,可以通过分析流道平行方向上剪切力的分布预测加工后各部位表面粗糙度Ra的情况。
2.2 置入2个圆柱体模芯时的工件内壁

图11 无模芯加工后的表面粗糙度
磨料流加工后,不同部位的表面粗糙度Ra如图12所示。加工后的表面的粗糙度随着加工循环次数的增加而减小。2处、3处比1处的表面粗糙度小,但加工循环次数超过30后,3个观察区域的表面粗糙度相近。这是由于图6中剪切速率的最大差值要比图4中的小,各部位受到的剪切应力相对较为均匀,随着加工循环次数的增加,剪切应力相对较大区域的表面粗糙度的减小速度率先放缓,而剪切应力较小区域仍有较大的表面金属去除率,因此当加工循环次数达到一定值时,不同的部位会得到相对较接近的表面粗糙度。但图12所得到的加工效果仍不十分理想,且需要较多的加工循环次数,既不经济又不高效。

图12 放置圆柱模芯加工后的表面粗糙度
2.3 置入与工件内壁形状相似模芯时的工件
上面的实验结果表明,当置入2个圆柱体的模芯后,加工表面剪切应力的均匀性有所改善,磨料流加工后得到的表面精度一致性有所改善。如图13所示,采用与工件内壁形状相似的模芯时,加工表面的粗糙度随着加工循环次数的增加而减小,20次循环加工后,部位3与部位2的表面粗糙度Ra的最大差值由无模芯时的0.376μm降为0.017μm。最终的表面粗糙Ra为0.250μm。因此在磨料流加工中可以通过设置模芯,使模芯与异形曲面之间形成等间距的流道,可以大大提高表面精度的一致性。
3 结论
(1)利用磨料流的性质和剪切速率与黏度之间的关系代数方程建立了一个幂律模型,通过COMSOL Multiphysics软件的CFD模块对这个数学模型进行了仿真分析,得到了磨料流在加工过程中的速度、剪切速率和剪切应力的分布情况。因此,非牛顿流体的幂律模型能够很好地模拟磨料流加工过程的流动情况。
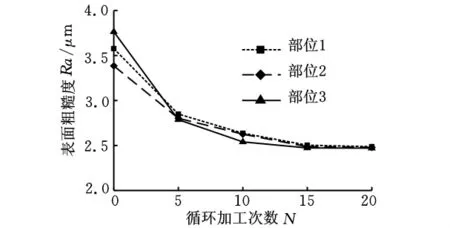
图13 放置相似模芯加工后的表面粗糙度
(2)未置入模芯时,异形曲面曲率变化较大部位的剪切速率和剪切应力要比曲率变化较小部位的剪刀速率和剪切应力大,因此曲率变化大的部位可以得到较高的表面精度。由于曲率变化小的部位所受到的剪切应力要小很多,因此无法得到一致的表面精度。当置入2个圆柱体的模芯时,加工表面各部位的受力情况发生了变化,与没有置入模芯时相比,各部位剪切应力的差值在减小。当加工循环次数达到一定值时,不同的部位可以达到较接近的表面粗糙度,但需要较长的加工时间。
(3)置入与工件异形内壁形状相似的模芯可以大大提高表面精度的一致性和加工效率。实验结果表明,工件内壁表面粗糙度Ra的最大差值由无模芯时的0.376μm降到置入与工件内壁形状相似模芯时的0.017μm。最终的表面粗糙度Ra达到0.250μm,大大提高了被加工表面的精度的一致性和加工效率。
[1]汤勇,陈澄洲,张发英.磨料流加工时磨料流动形态的研究[J].华南理工大学学报(自然科学版),1997,25(9):100-102.Tang Yong,Chen Chengzhou,Zhang Faying.Study on the Flowing State and the Practical Efficiency of Abrasive Flow Machining[J].Journal of South China University of Technology(Natural Science),1997,25(9):100-102.
[2]武利生,李元宗.磨料流加工研究进展[J].金刚石与磨料磨具工程,2005,2(1):69-72.Wu Lisheng,Li Yuanzong.Progress of Abrasive Flow Machining[J].Diamond & Abrasives Engineering,2005,2(1):69-72.
[3]Wang A C,Liang K Z,Liu C H,et al.High Precision Polishing Method in 3-D Surface and Elastic Abrasive Gel Development[C]//4th Asia Pacific Forum on Precision Surface Finishing and Deburring Technology.Taichung,2005:123-128.
[4]Loveless T R,Williams R E,Rajurkar K P.Study of the Effects of Abrasive Flow Machining on Various Machined Surfaces[J].Journal of Materials Processing Technology,1994,47(1/2):133-151.
[5]Tom K.Advanced Abrasive Flow Technologies[C]//4th Asia Pacific Forum on Precision Surface Finishing and Deburring Technology.Taichung,2005:129-138.
[6]Kim J D,Kim K D.Deburring of Burrs in Spring Collets by Abrasive Flow Machining[J].International Journal of Advanced Manufacturing Technology,2004,24(7/8):133-151.
[7]王阿成,白轩豪,陈韦达,等.流体研磨加工对工件表面的磨耗研究[C]//中国机械工程学会第二十四届全国学术讨会论文集.桃园,2008:3862-3866.Wang A C,Pai S H,Chen W D.Study of the Surface Wear in the Abrasive Flow Machining[C]//24th National Symposium of the Chinese Mechanical Engineering Society.Taoyuan,2008:3862-3866.
[8]赵培锋,轧刚.基于有限元方法的磨料流加工数值模拟[J].电加工与模具,2011(3):42-44.Zhao Peifeng,Ya Gang.Numerical Simulation of Abrasive Flow Machining Based on the Finite Element Method[J].Electromachining & Mould,2011(3):42-44.
[9]Gorana V K,Jain V K,Lal G K.Forces Prediction during Material Deformation in Abrasive Flow Machining[J].Wear,2006,260(1/2):128-139.
[10]Jain R K,Jain V K.Finite Element Simulation of Abrasive Flow Machining[J].Proceedings of the Institution of Mechanical Engineers,Engineering Manufacture B,2003,217(12):1723-1736.
[11]Jain R K,Jain V K.Stochastic Simulation of Active Grain Density in Abrasive Flow Machining[J].Journal of Materials Processing Technology,2004,152(1):17-22.
[12]Jain R K,Jain V K,Dixit P M.Modeling of Material Removal and Surface Roughness in Abrasive Flow Machining Process[J].International Journal of Machine Tools and Manufacture,1999,39(2):242-248.
[13]王时英,吕明,轧刚.磨料流加工的力学原理及应用[J].太原理工大学学报,1998,25(3):272-275.Wang Shiying,LüMing,Ya Gang.The Principle and Application of Abrasive Flow Machining(AFM)[J].Journal of Taiyuan University of Technology,1998,25(3):272-275.
[14]Walia R S,Shan H S,Kumar P.Determining Dynamically Active Abrasive Particles in the Media Used in Centrifugal Force Assisted Abrasive Flow Machining Process[J].The International Journal of Advanced Manufacturing Technology,2008,38(11/12):1157-1164.
[15]计时鸣,唐波,谭大鹏.基于VOF的模具结构化表面软性磨粒流数值模拟[J].中国机械工程,2011,22(3):334-339.Ji Shiming,Tang Bo,Tan Dapeng.Softness Abrasive Flow Numerical Simulation for VOF Based Structural Surfaces of Mould[J].China Mechanical Engineering,2011,22(3):334-339.

