新型3－RPC柔性精密平台的刚度与动力学分析

李仕华 龚 文 李富娟 姜 珊

燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

0 引言

并联机构满足了微动机器人运动分辨率高（纳米级）、响应快（数十赫兹）、体积小、精度高等要求［1］，因此微动机器人多采用并联机构，通常以柔性铰链代替传统运动副，来消除机械摩擦和间隙对精度的影响。

柔性并联机构刚度的理论分析对设计、制造一个柔性机构至关重要。当前，对柔性机构的刚度分析主要集中在柔性铰链的刚度分析［2－4］和平面柔性机构［5］的刚度分析，对空间柔性机构［6－7］刚度分析的研究成果并不多。对于空间柔性机构，通过建立其刚度的数学模型来获得良好的刚度性能，满足复杂工作条件下精确的操作要求。

在柔性机构动力学上，国内外大多数研究停留在对柔性机构的运动学分析及优化上，动力学方面的理论研究［8－9］不多，在一些需要高精度或振动环境的工况下，基于运动学的控制方法往往不能很好地达到实际应用要求。本文提出一种新型柔性机构，并在刚度分析的基础上，对该柔性机构进行了动力学分析。

1 3－RPC柔性精密平台模型

如图1所示，新型3－RPC柔性精密平台由固定平台、动平台及3个RPC分支组成，每个分支由柔性R副、柔性P副和柔性C副构成。为获得空间立方体工作空间，3个分支采用空间正交布置方式，该平台具有3个自由度，即沿着x、y、z轴的移动。该柔性精密平台工作时由3路压电陶瓷驱动器驱动，能完成空间微／纳米级操作。该平台具有结构紧凑、运动解耦、易于控制、精度较高等优点，具有很好的应用前景。

2 刚度分析

2.1 柔性运动副的刚度

组成分支的柔性运动副的基本柔性单元为半圆弧形柔性铰链，如图2所示，r为切口圆弧半径，b为铰链宽度，t为柔性转动副最薄弱处的厚度。

图2 半圆弧柔性铰链

半圆弧柔性铰链的柔度矩阵在图2建立的坐标系中可表示为

元素c1～c8的具体表达式参见文献［10］。

柔性P副采用的是柔性桥式微位移放大机构。该机构采用全对称设计，由刚性梁和半圆弧柔性铰链组成，并应用线切割技术在一块金属材料上加工而成。图3中，l、a、a1分别为柔性移动副中两柔性转动副之间的长度、厚度和空隙长度，t1为柔性移动副中转动副最薄弱处的厚度，r2为柔性移动副中转动副的切口圆弧半径。

图3 结构Ⅰ简图

根据图3，柔性铰链在局部坐标系Aixaiyaizai（i＝1，2）下的柔度矩阵Ci可以通过坐标变换变换到坐标系Bixbiybizbi，转换公式为

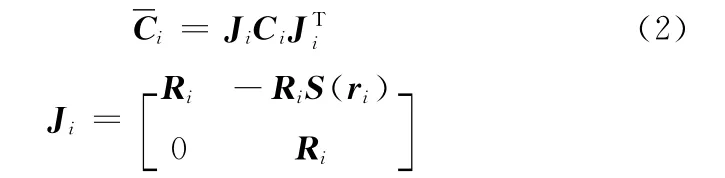
如图4所示，柔性移动副由结构Ⅰ、结构Ⅱ、结构Ⅲ、结构Ⅳ组成，结构Ⅰ、结构Ⅱ串联形成柔性移动副的右半部分，结构Ⅲ、结构Ⅳ串联形成柔性移动副的左半部分，结构Ⅰ、Ⅱ与结构Ⅲ、Ⅳ以并联形式连接固定端和输出端。分别求出结构Ⅰ、Ⅱ、Ⅲ、Ⅳ的刚度或柔度矩阵，通过柔度矩阵变换法，建立柔性微位移放大机构的刚度矩阵：

图4 柔性移动副

其中，Ry（＊）为局部坐标系到坐标系O2x2y2z2下绕y轴的旋转矩阵（下同），如图4所示。

同理，可建立柔性C副的刚度矩阵，柔性C副由2条串联分支EiFiGi组成，如图5所示，每条分支包含柔性铰链Ei、Fi、Gi，因此柔性C副的刚度矩阵为

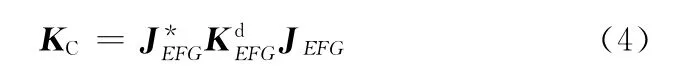
图5中，w为柔性圆柱副内部长度，l3为柔性圆柱副中两转动副之间距离，r3为柔性圆柱副中转动副的切口圆弧半径。

图5 柔性圆柱副C

2.2 分支刚度矩阵

以分支1为例，分支1由1个柔性转动副R、1个柔性移动副P、1个柔性圆柱副C组成。选择动平台中心P为参考点，如图6所示，在每个柔性运动副建立局部坐标系，因此它们相对于参考坐标系的柔度变换矩阵可写成

其中，l1为坐标系Pxyz原点到坐标系O1x1y1z1的距离；l2为坐标系O1x1y1z1原点到坐标系O2x2y2z2的距离；a0为柔性圆柱副两侧的厚度；h为正方体上平台的边长；rO1、rO2、rO3分别为O1O、O2O、O3O在局部坐标系O1x1y1x1、O2x2y2x2、O3x3y3x3下的表示，如图6所示。

分支1的柔度矩阵为

式中，Jc1为分支1由局部坐标系到参考坐标系的变换矩阵；J1、J2、J3分别表示柔性R副、柔性P副、柔性C副建立的局部坐标系到参考坐标系的变换矩阵；Cd为分支1的柔

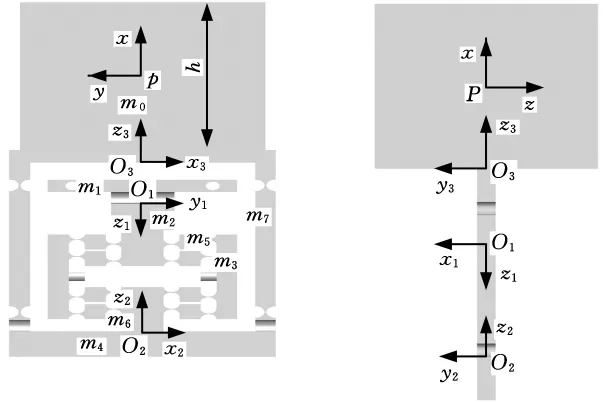
图6 分支1柔度坐标系

参考坐标系Pxyz下，分支1的刚度矩阵为

同理，分支2和分支3柔度矩阵分别为

其中，柔度变换矩阵Jc2、Jc3由式（5）和分支2与分支3的具体参数推导而得。

参考坐标系Pxyz下，分支2和分支3的刚度矩阵为

2.3 整体刚度矩阵

3－RPC柔性精密平台由3个相同分支以并联形式组成，考虑到每个分支刚度模型的局部坐标系与整体刚度模型的参考系Pxyz重合，转换矩阵Joj（从第j（j＝1，2，3）支链的局部坐标系Ojxjyjzj到参考坐标系Oxyz转换矩阵）变为单位矩阵。整体刚度矩阵为

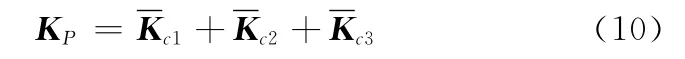
将整体刚度矩阵KP转换到参考坐标系Hxyz中，参考坐标系的原点位于动平台上表面的中心，则转换后刚度矩阵KH为

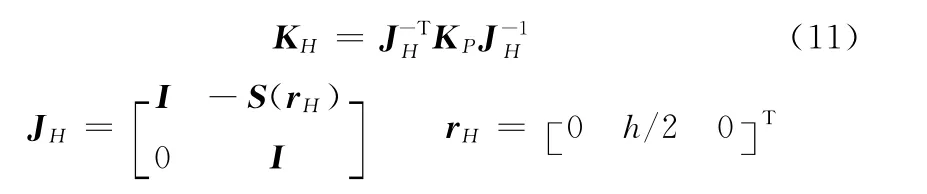
参照表1、表2中参数和材料属性，利用MATLAB计算参考点H刚度矩阵的KH：

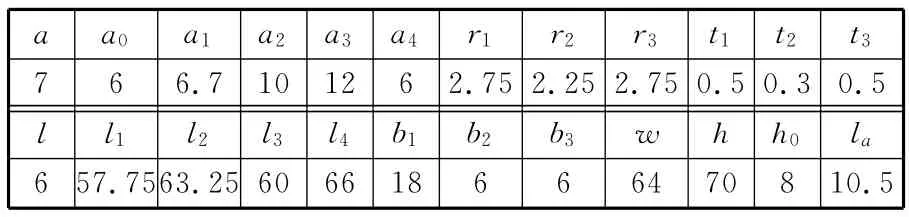
表1 3－RPC并联微动机构几何参数 mm

表2 Ti－6Al－4V合金材料属性

2.4 有限元分析

采用ANSYS对平台的刚度进行了仿真分析。每个分支添加了2个固定约束，在动平台的上表面施加1个作用力，材料属性选择钛铝合金，几何结构参数见表1。

首先，施加外力Fy＝－1N作用在动平台上表面的中心H，在H坐标系z轴负向取一点H1，并满足HH1＝dz，dz为测量点在z方向的位移，如图7所示。可测得点H、H1处的位移yH、yH1，得到

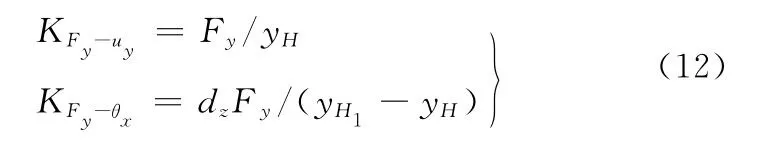
式中，KFy－uy为Fy引起的y方向位移所产生的刚度；KFy－θx为Fy引起绕y轴转动所产生的刚度。

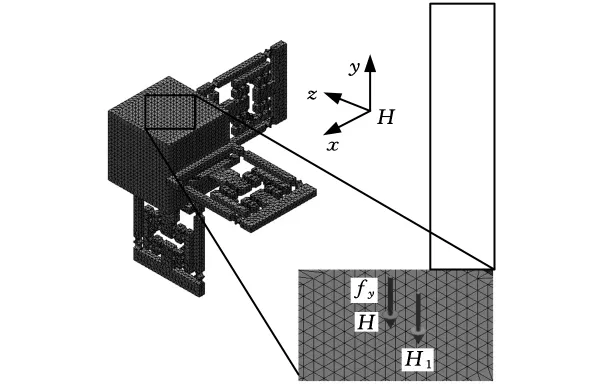
图7 有限元分析模型

然后，施加外力Fy＝－1N作用于点H1处，将产生一力偶mx绕x轴转动，点H、H1的位移yH、yH1测出后，通过下式计算刚度：

式中，Kmx－θx为mx引起的x方向转动所产生的刚度。

具体的计算结果见表3。

表3 平台的刚度

有限元结果和理论结果还存在8%左右的误差，刚度建模将连接柔性单元的连杆等效为刚性杆，忽略了其柔性特性对刚度模型的影响，这是造成误差的主要原因，但误差在合理范围内。

2.5 结构参数对刚度的影响

根据建立的平台刚度模型，以刚度KFy－uy为指标，绘制了几何结构参数a0、a、l1、l2、l3、l4、h、w改变时，刚度的变化情况，见图8、图9。

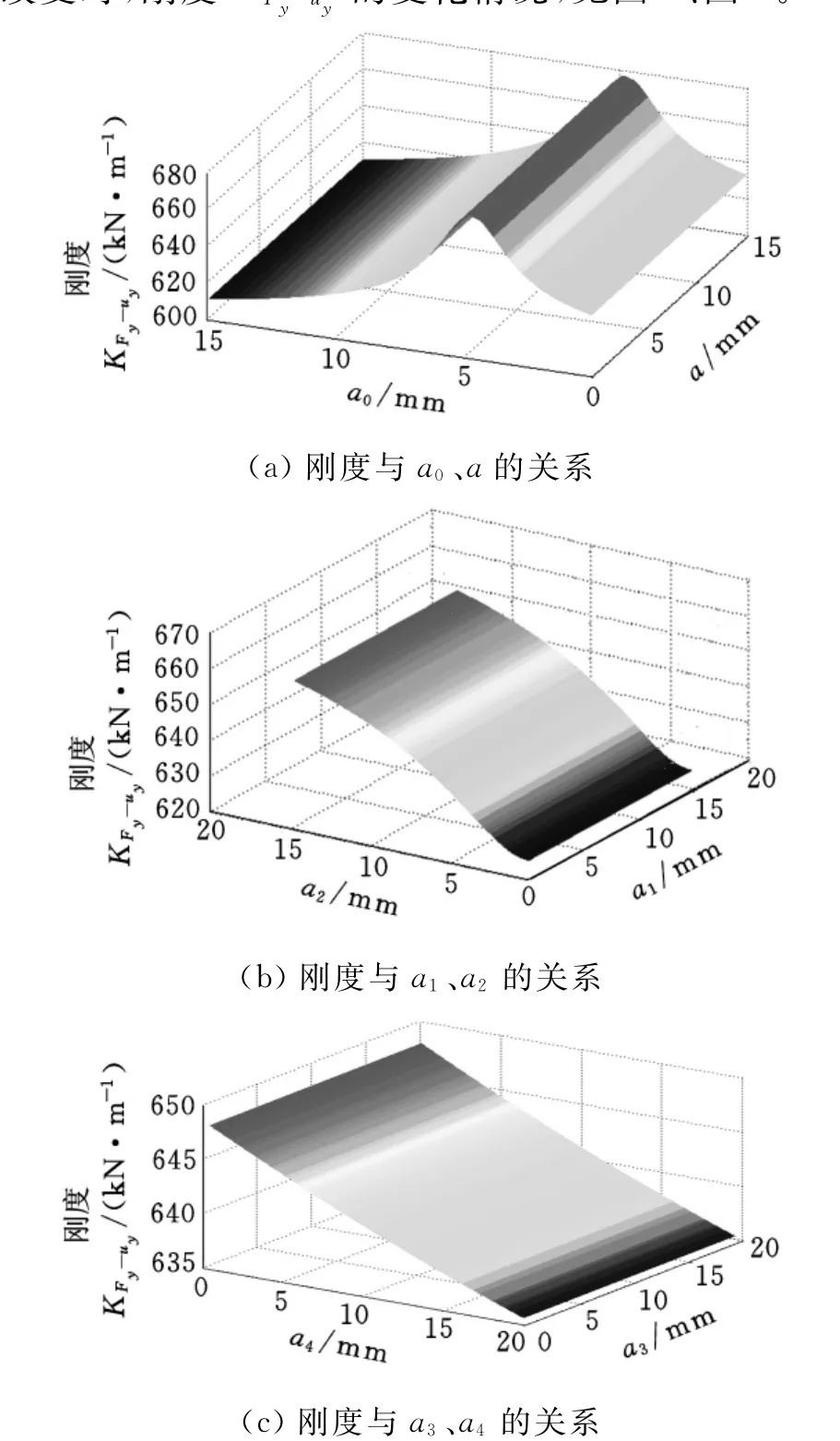
图8 结构参数和刚度之间关系Ⅰ

从图8、图9可以看出，刚度KFy－uy随着结构参数a0、a的增加而增大，当a0＝a＝4.5mm时出现了一个峰值，而后又逐渐减小（图8a）；随着结构参数a1、a2的增大而非线性增大（图8b）；随参数a3、a4的增加呈线性减小（图8c）；随结构参数l1、l2的增加而增大，在l1＝l2＝42mm达到一个峰值后又非线性递减（图9a）；随参数l4、h0非线性递减（图9b、图9c）；随结构参数h、w的增加而增大，在h＝w＝52mm达到一个峰值后又非线性递减（图9d）。

3 动力学分析

3.1 动力学方程的建立

利用拉格朗日方法建立机械系统的动力学方程。该方法只需计算系统的动能和势能，不需考虑约束力的影响。选取广义坐标q＝［q1q2q3］T，平台的动能和势能可用选取的广义坐标及其变化形式表示。

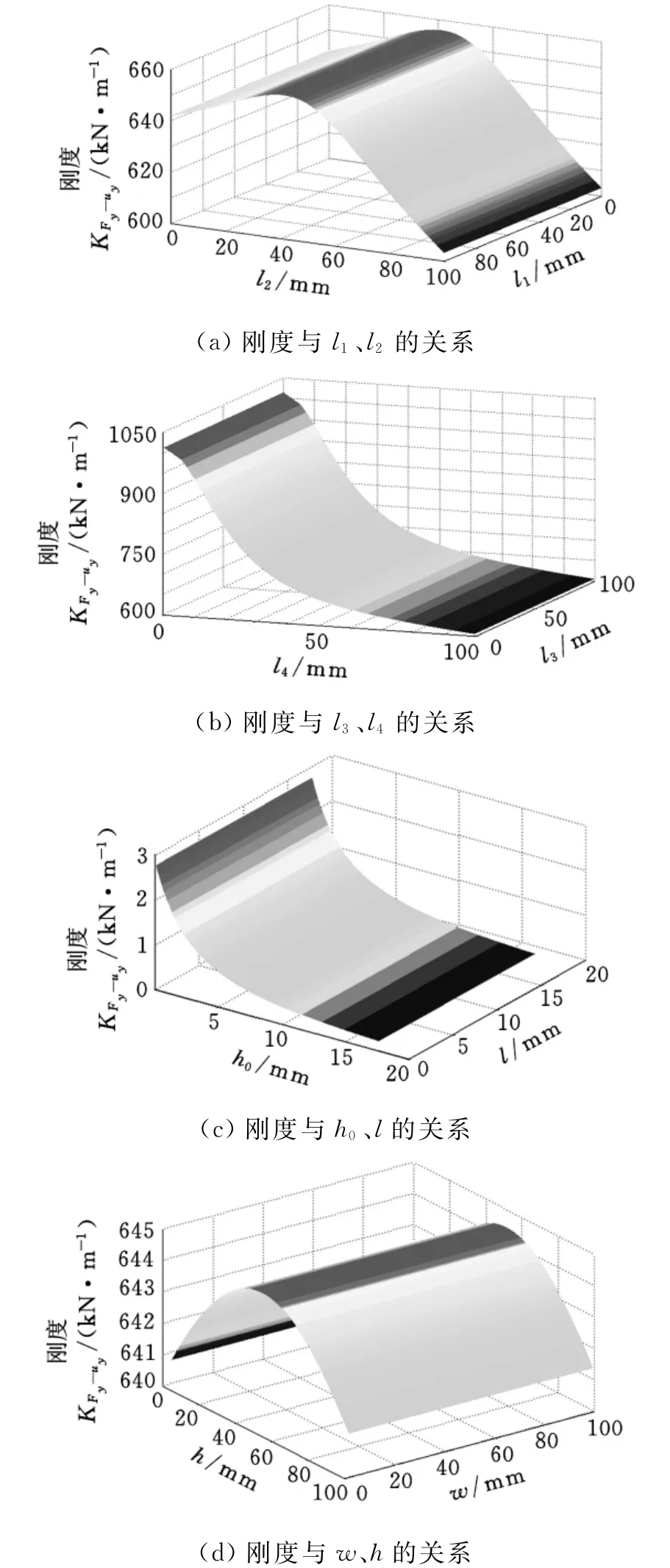
图9 结构参数和刚度之间关系Ⅱ

柔性转动副R的能量方程为

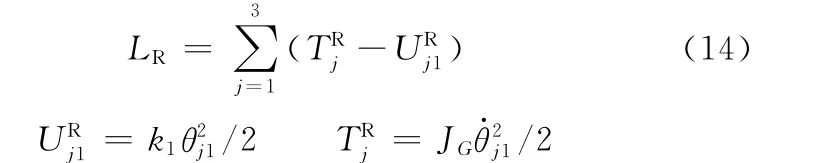
柔性移动副P的能量方程为

柔性圆柱副能量方程为

以第二分支为例，柔性圆柱副C的动能为

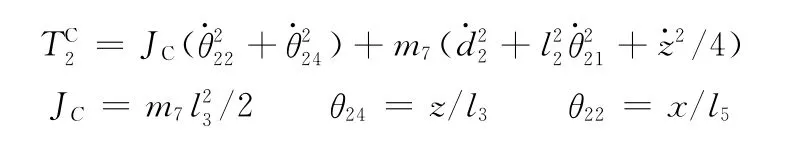
柔性圆柱副C的弹性势能为

同理，其他2个分支的动能与势能很容易求得。

机构的动平台的势能只来源于重力，因此动平台的动能为

机构的重力势能为

其中，m0～m7如图6所示。

机构拉格朗日方程为

式中，LR、LP、LC分别为柔性转动副R、移动副P、圆柱副C的能量表达式。

拉格朗日方程一般形式为

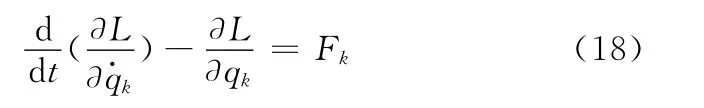
式中，qk为第k个广义坐标；Fk为第k个驱动力。

根据式（18），再考虑各变量与广义坐标之间关系，可推导出微动机构动力学方程为

式中，G为重力矩阵；F为驱动力矩阵；F1、F2、F3分别为第一、第二、第三分支的驱动力；A为放大器的放大倍数；k1为第i分支第一个柔性转动副R的一个近似转动刚度；k2为第i分支柔性移动副P的一个近似刚度；k3为第i分支柔性圆柱副C的一个近似刚度。

微动平台的自然频率为

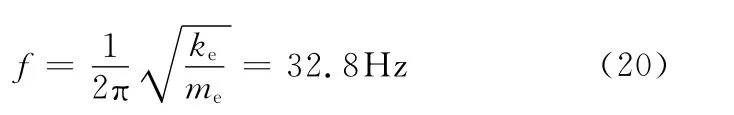
3.1 模态分析和有限元仿真验证

基于振动理论，对机构进行了模态分析和有限元仿真验证。由有限元仿真可以分析得到表4的结果。通过表4所示的有限元结果与式（20）所计算的理论值进行对比，可以看出，理论值和有限值存在10.8%的误差，原因是桥式位移放大器理论模型没有考虑变形对柔性铰链转动惯量的影响，但误差在合理范围内，验证了理论模型的合理性。

表4 机构前6阶自然频率 Hz

表4中的前3阶振型是分别沿着3个坐标轴的移动，后3阶振型是分别绕着3个坐标轴的转动。由于机构结构的对称性，前3阶自然频率相等，后3阶自然频率也相等。

自然频率随r1、r2、r3的增大而均呈现非线性递减，随r1的变化如图10a所示；自然频率随b1、b2、b3的增大均呈现线性递增，随b1的变化如图10b所示；自然频率随t1、t2、t3的增加均呈现非线性递增，随t1的变化如图10c所示。柔性铰链结构参数对频率影响的研究有利于设计面向工程需要的三维微动平台。

图10 自然频率与柔性铰链参数变化曲线

4 结论

（1）提出了一种新型3－RPC并联精密平台，该平台具有结构紧凑、运动解耦、易于控制、精度较高等优点，具有很好的应用前景。

（2）采用柔度矩阵变换法建立了新型空间并联柔性精密平台的刚度模型，并用有限元方法对刚度模型进行了验证，讨论了柔性铰链结构参数对平台刚度的影响。

（3）采用拉格朗日法建立了柔性精密平台的动力学方程，并利用有限元对其进行了模态分析，得到了柔性精密平台的前6阶振动频率；进一步讨论了柔性精密平台的自然频率与柔性铰链参数变化规律。

［1］贾庆轩，魏秋霜，孙汉旭，等.并联微动机器人的研究现状［J］.山东理工大学学报，2003，17（6）：98－102.Jia Qingxuan，Wei Qiushuang，Sun Hanxu，et al.Current Research Status of Parallel Jiggle Robots［J］.Journal of Shandong University of Technology，2003，17（6）：98－102.

［2］Tian Y，Shirinzadeh B，Zhang D.Closed－form Compliance Equations of Filleted V－shaped Flexure Hinges for Compliant Mechanism Design［J］.Precision Engineering，2010，34（3）：408－418.

［3］Zelenika S，Munteanu M G，De Bona F.Optimized Flexural Hinge Shapes for Microsystems and High－precision Applications［J］.Mechanism and Machine Theory，2009，44（10）：1826－1839.

［4］Tian Y，Shirinzadeh B，Zhang D，et al.Three Flexure Hinges for Compliant Mechanism Designs Based on Dimensionless Graph Analysis［J］.Precision Engineering，2010，34（1）：92－100.

［5］刘平安.柔性关节及3－DOF微动平面并联机器人设计与分析［D］.北京：北京交通大学，2008.

［6］Pham Hy－Hoang，Chen I－Ming.Stiffness Modeling of Flexure Parallel Mechanism［J］.Precision Engineering，2005，29（4）：467－478.

［7］Dong Wei，Sun Lining，Du Zhijiang.Stiffness Research on a High－precision，Large－workspace Parallel Mechanism with Compliant Joints［J］.Precision Engineering，2008，32（3）：222－231.

［8］Zhang Xianmin，Hou Wenfeng.Dynamic Analysis of the Precision Compliant Mechanisms Considering Thermal Effect［J］.Precision Engineering，2010，34（3）：592－606.

［9］贾晓辉，田延岭，张大卫.基于虚功原理的3－RRPR柔性精密定位工作台的动力学分析［J］.机械工程学报，2011，47（1）：68－73.Jia Xiaohui，Tian Yanling，Zhang Dawei.Inverse Dynamics of 3－RRPR Compliant Precision Positioning Stage Based on the Principle of Virtue Work［J］.Chinese Journal of Mechanical Engineering，2011，47（1）：68－73.

［10］Koseki Y，Tanikawa T，Koyachi N，et al.Kinematic Analysis of Translational 3－DOF Micro Parallel Mechanism Using Matrix Method［C］／／IEEE／RSJ International Conference on Intelligent Robots and Systems.Takamatsu，Japan，2000：768－792.