空间机械臂在轨刚度计算与验证
毛嘉炜,贺帅,刘昌儒,吴清文,4,徐振邦,4,谢宗武,母德强
(1.中国科学院,长春光学精密机械与物理研究所,吉林长春 130033;2.中国科学院大学,北京 100049;3.中国科学院,空间光学系统在轨制造与集成重点实验室,吉林长春 130033; 4.中国科学院大学材料与光电研究中心,北京 100049;5.哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001;6.长春工业大学机电工程学院,吉林长春 130012)
0 前言
随着科学技术的不断发展,各国在太空层面进行了进一步探索。但是太空环境有着微重力、高真空、高寒、大温差、强辐射的特性,阻碍了对太空的进一步探索,尤其是载人航天工程。在恶劣的空间环境下,人类许多空间活动很难完成,因此空间机械臂的研究成为太空探索的重要基础。自1981年哥伦比亚号航天飞机在太空中首次采用机械臂以来,国际空间站(ISS)的加拿大臂(CANADARM2)、欧洲臂(ERA)、日本臂(JEMRMS)等在外太空操作中起到了非常重要的作用。随科技的进步,对于空间机械臂技术的需求越来越迫切,而且对其工作能力和性能、可靠性、安全性、寿命等方面也提出了越来越高的要求。
空间机械臂是一个机、电、热、控一体化集成系统,建立准确的运动学、动力学模型和相关的仿真分析、实验验证是实现机械臂功能的保障。机械臂在轨状态要保证相应的控制性能与运动精度,也要求确保机械臂的结构刚度。其刚度特性是影响整体运动学的主要因素,为此对其在轨刚度进行准确模拟分析。目前,国内对于空间机械臂刚度的分析方法和实验方法研究较少,也少有学者将柔度矩阵建模与机械臂构型相结合,国外的相关资料也有限。MUSSA-IVADI和HOGAN给出了冗余度串联机械臂的柔度矩阵和刚度矩阵。DIMENTBERG第一次运用旋量理论求出刚体在平衡位置的刚度矩阵。赵朋飞针对已有刚度矩阵算法进行重构与优化,但是该研究只是对串联机械臂末端工具的刚度进行了分析。陈少帅对谐波传动引起的刚度变化进行分析。上述研究只考虑了谐波减速器与力矩传感器等具有明显柔性特征的部件的柔度,而忽略了其他部件的柔度。而空间机械臂具有高轻量化的特点,其他部件的柔度会引起更大的误差,不能忽略,可以采用有限元分析的方法计算机械臂的整体柔度。
采用有限元计算机械臂在一种构型下的柔度时,需要在有限元软件中旋转7个关节并重新进行连接和计算,该过程约耗时4 h。而机械臂实际工作时的构型有无穷多种,采用有限元分析对各个构型进行建模与分析工作量巨大且不切实际。因此,应采用新的方法分析机械臂在不同姿态下的柔度。
针对上述情况,本文作者提出一种将经典柔度理论与经典机器人运动学理论相结合的计算方法,计算机械臂在各个位姿下的整体柔度矩阵,并据此预估机械臂抓取载荷的基频。该方法充分考虑机械臂各部件的柔度影响,其理论分析与有限元分析计算的柔度偏差为3.4%、基频偏差为1%,说明了其理论计算方法的准确性。利用该方法可将计算机械臂在一种构型下的柔度矩阵的时间由4 h减小到10 ms,大大提高计算效率。
1 机械臂运动学建模
文中的研究对象是一个七自由度的空间机械臂,由2个臂杆、7个关节、2个末端执行器、2台手眼相机、2台肘部相机组成。机械臂零位构型如图1所示,其零位时的坐标系如图2所示。基座坐标系{0}的原点位于基座末端作用器端面中心点,轴方向垂直于相机。末端坐标系的原点位于末端作用器端面中心点,轴方向垂直于相机。相应的D-H参数见表1,则末端相对基座的齐次变换矩阵为

表1 机械臂D-H参数
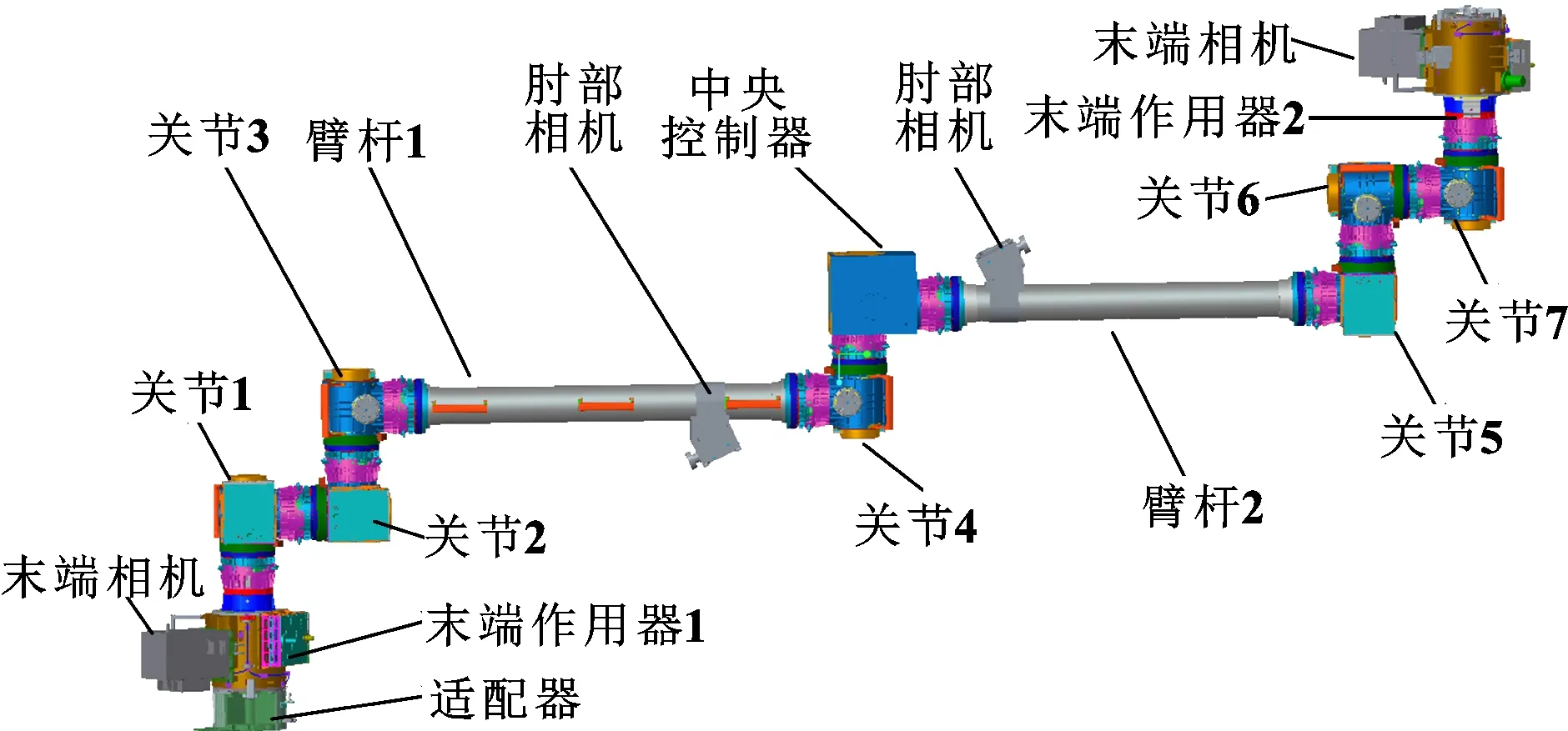
图1 空间机械臂零位构型
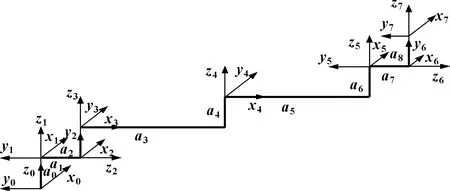
图2 空间机械臂零位构型坐标系
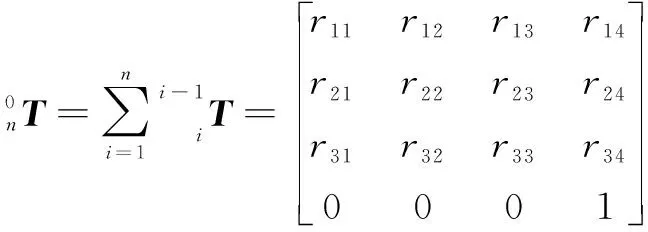
(1)
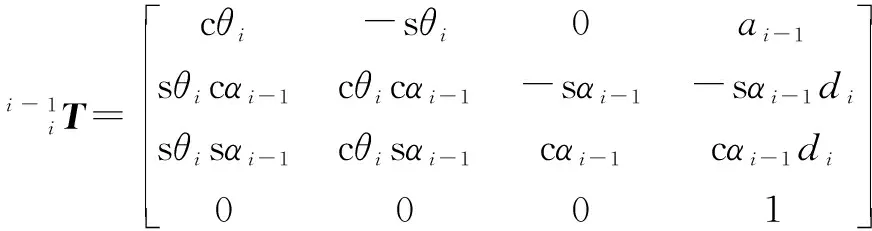
(2)
机器人的正运动学即给定关节转动角度求解末端位姿(角度采用欧拉角321表示)。将各关节角度代入式(1)可以求得齐次变换矩阵,则相应的末端位姿为
===
(3)
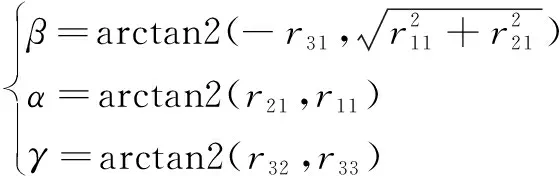
(4)
当=±90°时

(5)
当=90°时
=0,=arctan2(,)
(6)
当=-90时
=0,=-arctan2(,)
(7)
2 柔度理论建模
2.1 单元柔度矩阵变换

图3 单元柔度矩阵变换
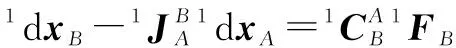
(8)
其中:
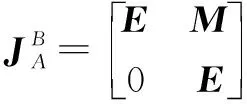
(9)

(10)
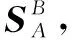
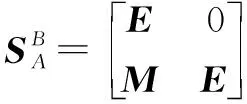
(11)

(12)
点受到的力在坐标系{0}下与在坐标系{1}下关系式为

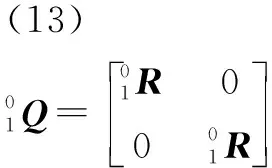
(14)
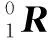
则:
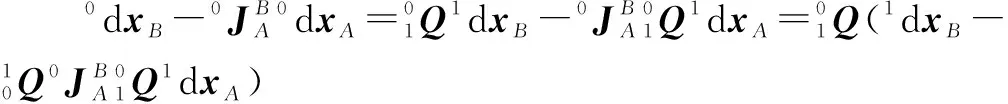
(15)
对应图中单元,点受到的力向点等效时,在坐标系{1}下的描述为
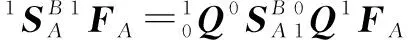
(16)
则:

(17)

(18)
从而推导出单元在坐标系{0}下的柔度矩阵与在坐标系{1}下的柔度矩阵的关系为
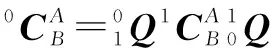
(19)
2.2 单元柔度矩阵

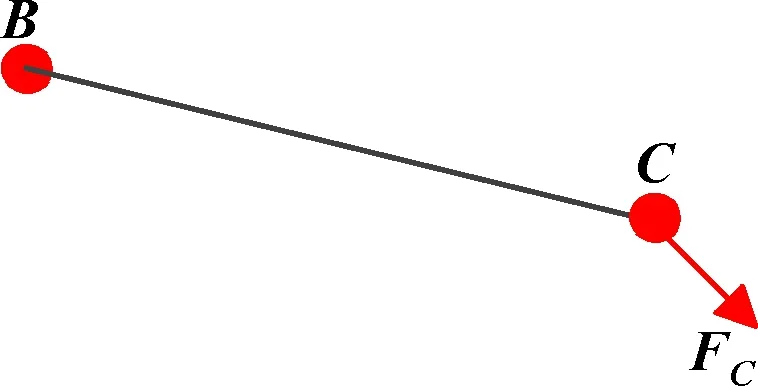
图4 单元柔度矩阵模型
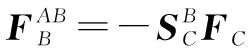
(20)
则有:

(21)
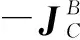
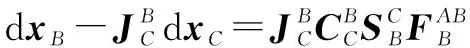
(22)

(23)
2.3 串联单元柔度矩阵
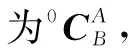

图5 单元串联模型

(24)
其中:
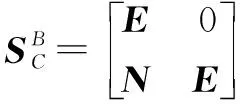
(25)
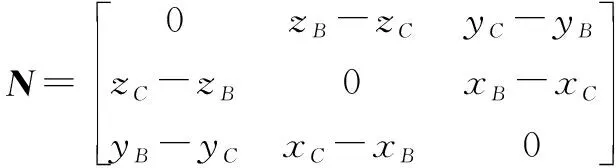
(26)
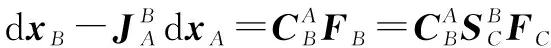
(27)

(28)
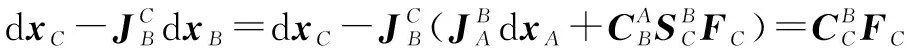
(29)

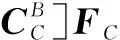
(30)
所以串联后点相对点的柔度矩阵为
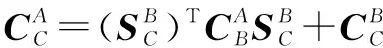
(31)
2.4 镜像单元柔度矩阵

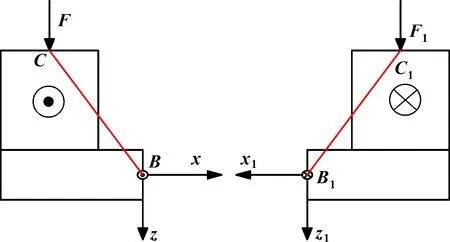
图6 镜像单元模型

(32)

(33)
2.5 整机柔度矩阵
将个连杆的柔度矩阵串联,得到整机柔度矩阵。将相对连杆坐标系的柔度矩阵转换到世界坐标系下,得到转换后的柔度矩阵:

(34)
利用串联柔度矩阵公式(31),依次求得前个连杆串联后的柔度矩阵:

(35)
3 机械臂刚度理论模型与实验对比
3.1 刚度矩阵理论验证
在轨工作状态时,机械臂需要抓取3 t货物。为满足机械臂的控制需求,需要分析其不同构型下抓取3 t物体的基频。因此,为验证柔度矩阵理论模型的准确性,对机械臂2种构型进行有限元分析,对应有限元模型如图7所示,其构型参数见表2。采用柔度矩阵算法与有限元分析分别计算2种构型下的柔度矩阵,结果如表3所示。可知,主对角值最大偏差为3.4%,该偏差主要来源于有限元D-H参数与理论D-H的参数偏差。同时,非对角线参数存在较大的偏差,是由于主对角线参数比其他项参数大几个数量级,矩阵运算时主对角线参数与非主对角线参数耦合导致的。
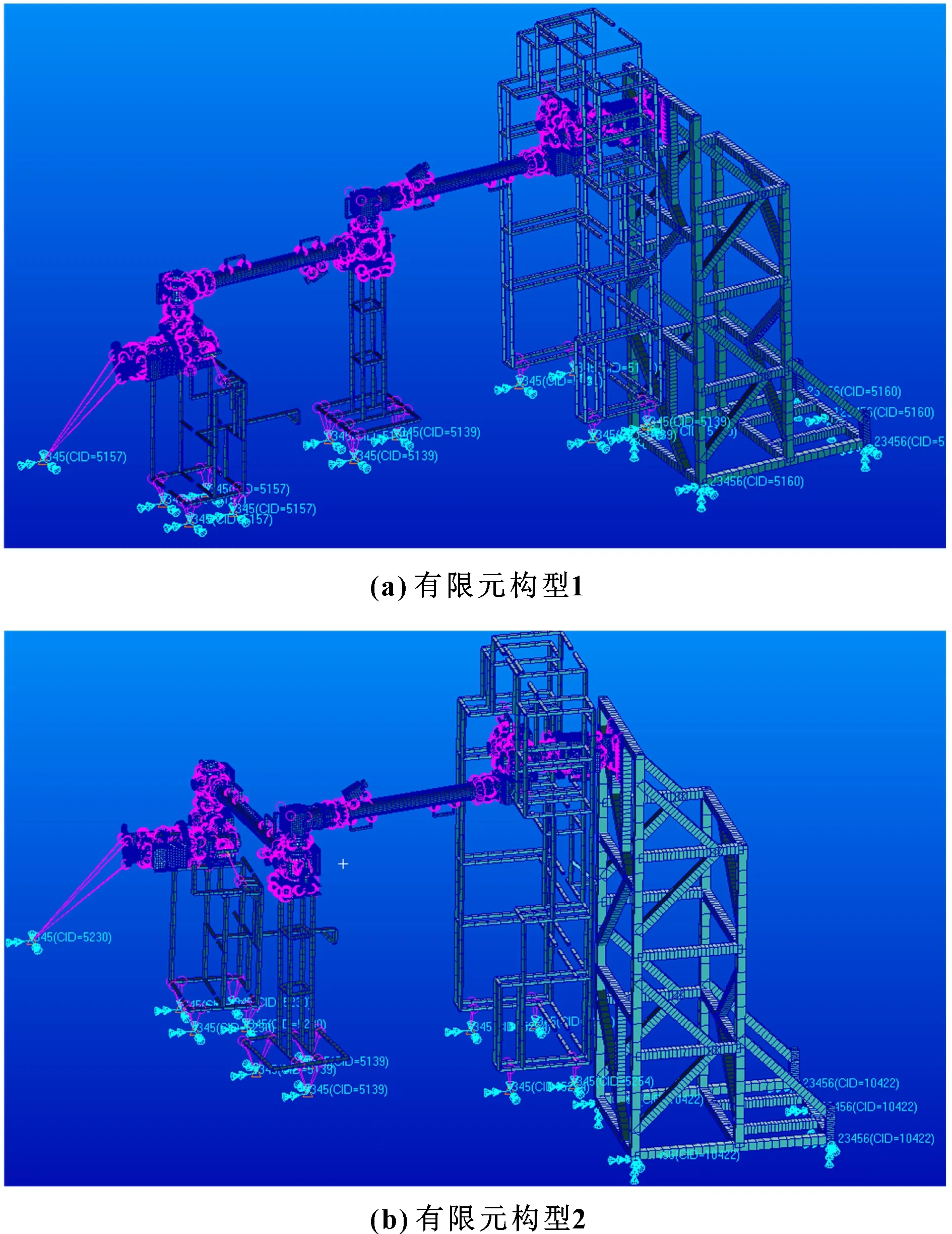
图7 机械臂测试状态下模型

表2 机械臂2种构型下的关节角度 单位:(°)
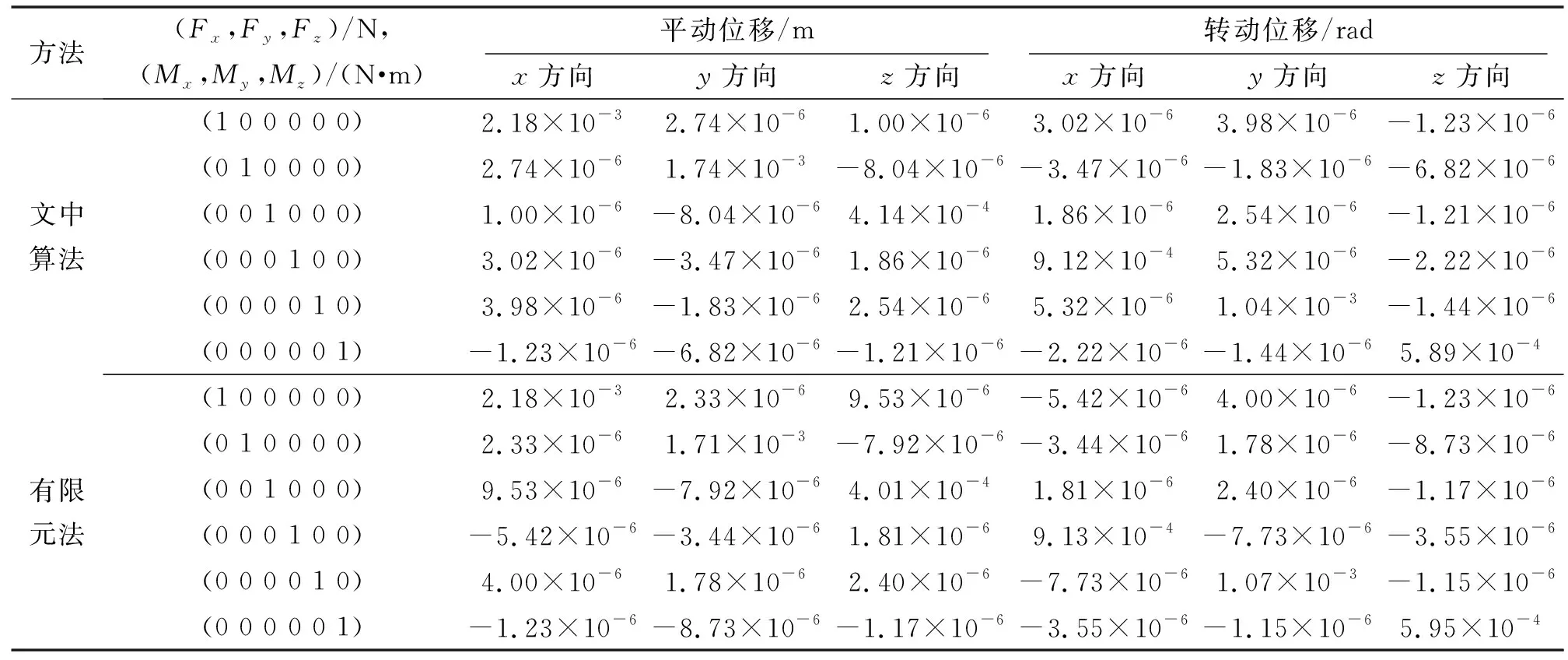
表3 机械臂连杆柔度矩阵
采用柔度矩阵理论模型进行在轨基频分析时,机械臂的质量难以精确,为此需要对机械臂质量进行相关等效分析。由于机械臂负载较大,机械臂自身质量特性对在轨基频的影响相对较小,将机械臂质量的1/2等效到末端负载上。下面是对该等效方法的偏差估计。
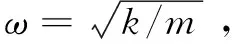
则:

(36)
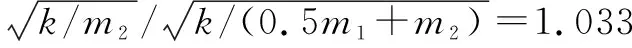
(37)
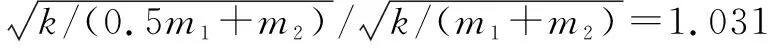
(38)
因此,将机械臂质量的1/2等效到末端负载上的偏差可控制在3%左右,由于此计算方法考虑的是单自由度频率,而实际机械臂采用多自由度柔度矩阵,计算结果会存在一定差异。选取表中2个典型构型进行理论计算与有限元分析,结果如表4所示。可知理论计算结果与有限元分析结果最大比值为1.01,产生该偏差的主要原因:(1)理论分析时机械臂质量等效到负载上时存在一定误差;(2)有限元中的D-H参数与机械臂实际的D-H参数存在一定偏差。
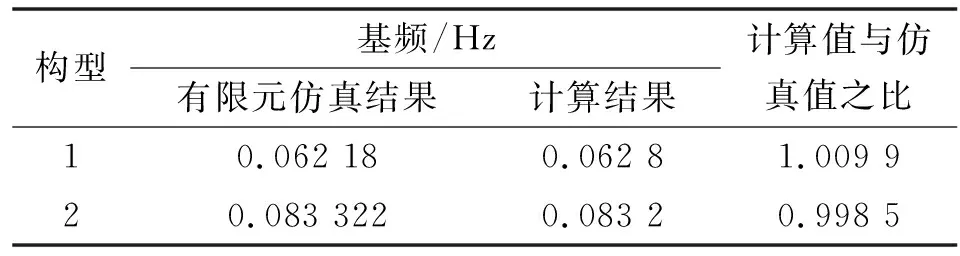
表4 机械臂基频分析结果
3.2 实验验证
为得到柔度矩阵理论模型与实验测试结果的偏差以验证此计算方法的准确性,对机械臂2种构型进行测试,其构型参数同表2。
基频测试时将机械臂一端固定在模拟墙上,机械臂各主要单元由气浮工装实现重力卸载,在负载上施加一定的力使机械臂偏离平衡位置,同时用激光跟踪仪记录机械臂末端位移。
实验时增加了气浮工装的质量、气浮桁架的刚度等因素,因为模拟墙的质量与刚度偏低,导致得到的基频结果也偏低。通过测试实验得到的结果如表5所示。机械臂抓取物体时的柔度理论模型计算结果比实验测试结果偏高,柔度理论模型计算结果与测试结果之比为1.071 8,故柔度矩阵算法计算的基频与实验结果的偏差为7.2%,说明利用该算法能够较准确地计算机械臂的在轨基频。
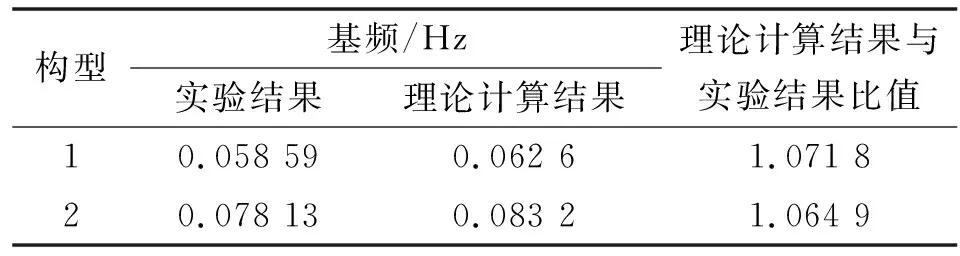
表5 模拟墙测试状态下基频分析结果
4 结论
本文作者提出一种基于柔度理论建模的计算方法,相较于常见柔度矩阵只考虑关节处柔度的分析方法,文中柔度矩阵理论方法考虑了机械臂各连杆中主要零件的柔性,并根据连杆柔度矩阵计算机械臂各个位姿下的整体柔度矩阵,然后将机械臂整体柔度矩阵用于机械臂的在轨基频预估。柔度矩阵偏差为3.4%,理论分析基频与有限元计算基频偏差为1%,验证了所提出的柔度理论建模方法对机械臂在轨基频计算的准确性。而理论分析基频与实验基频偏差为7.2%,偏差主要来源于有限元仿真,但满足工程上10%的偏差要求。相对于在采用有限元计算在轨基频时需要建立各种构型,柔度理论算法将柔度矩阵与机械臂构型相结合,能快速计算机械臂在不同构型下的基频,具有工程应用价值。

