基于混合参数蚁群算法的移动机器人路径规划

荆学东，杜黎童，郭泰，蔡震寰

(上海应用技术大学机械工程学院，上海 201418)

0 前言

全局路径规划是研究室内移动机器人运动控制的重点技术之一。移动机器人根据自身所处的全局地图环境和目标点的信息，它可以迅速地通过自主计算找到一条从当前位置到达指定目标点的适宜路径。路径规划的算法许多，主要有A算法、栅格解耦法和人工势场法、神经网络算法、遗传算法和粒子群算法等。

蚁群算法(Ant Colony Optimization,ACO)是由意大利学者DORIGO等提出的一种群集智能算法。算法早期主要是用来解决商旅问题，随着算法的应用发展，且ACO算法本身具备的分布式计算、正反馈性和强鲁棒行等特点，它也广泛应用到路径规划领域，并且取得了许多优秀成果。虽然ACO算法优点很多，但也存在许多缺点。对它的缺点，STÜTZLE、HOOS提出了最大最小蚁群系统；文献[14]提出了把ACO算法和遗传算法(Genetic Algorithm,GA)结合使用的混合算法(Genetic Algorithm-Ant Algorithm,GAAA)；文献[15-18]则把GAAA算法成功运用到旅行商、车间调度等生产生活的问题中去。本文作者设计了一种混合参数的蚁群进化算法(Hybrid Parameter Ant Colony Evolutionary Algorithm,HPACEA)，此算法在GA算法和ACO算法融合节点和衔接处进行优化改进，并通过实验验证了该算法的可行性和有效性。

1 基于栅格地图的环境建模

文中的室内移动机器人搭载单线激光雷达，它无法获取周围物体的高度信息，仅能获取平面数据，扫描数据为二维数据。为简化室内环境，采用栅格地图法对移动机器人获得的室内环境数据进行建图，栅格尺寸大小与移动机器人的外形大小有关，用黑白2色栅格表示不可行路径节点和可行路径节点。为保证机器人和障碍物有安全的间隔距离，根据机器人实际尺寸取边长的二分之一长度对障碍物进行“膨化”处理，用黄色栅格表示膨化处理的安全距离空间。当雷达数据映射到地图中时，如果障碍物面积不足一个栅格，则当作占据一个完整栅格。文中栅格地图中每个栅格的序号从左上角开始，依次编号为1、2、…、。对环境进行栅格建图，如图1所示。

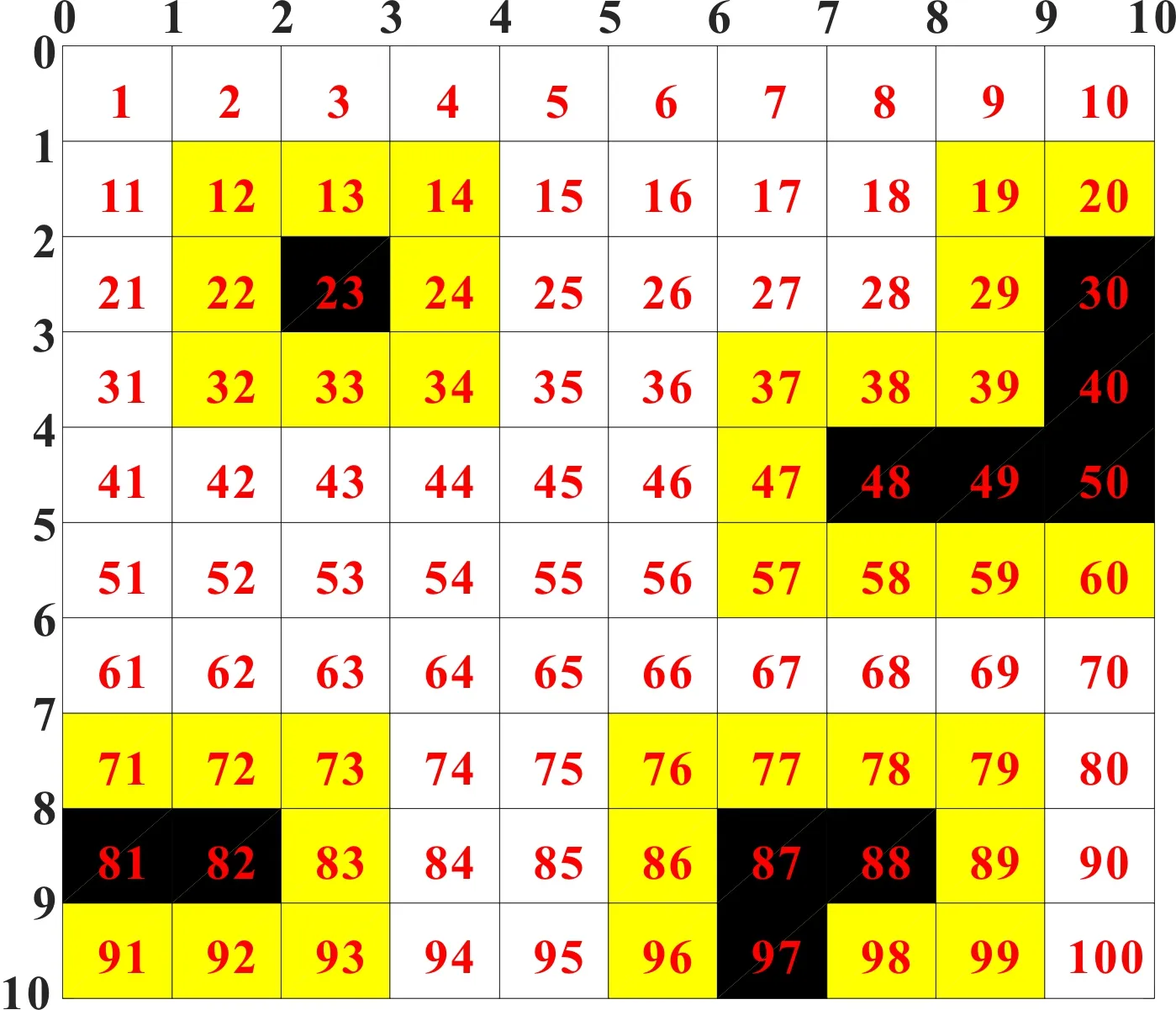
图1 栅格法的环境地图

2 混合参数蚁群进化算法的原理与改进

本文作者提出的混合参数蚁群进化算法(HPACEA)的总体框架如图2所示。

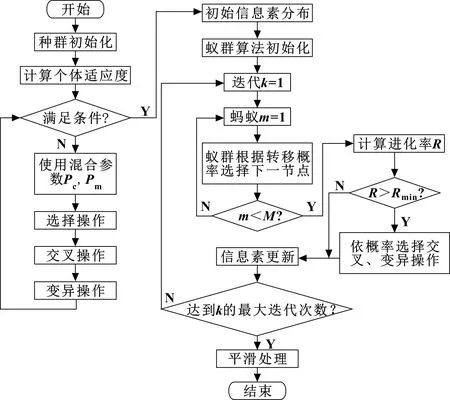
图2 HPACEA算法框架

2.1 HPACEA中遗传算法的设定

2.1.1 交叉概率和变异概率的改进

为增加算法初期蚁群信息素分布的多样性，对遗传算法的交叉概率和变异概率引入高斯变异算子。首先在种群每次迭代中随机在区间[0.2，0.9]中选择交叉概率，然后对该交叉概率随机选择一定数量的维度进行高斯变异操作，生成的满足+=1。其操作方式为

=roundn(0.2+0.7×rand(),-1)

(1)

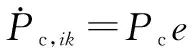
(2)

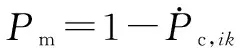
(3)

式中:～(1,1),(1,1)表示均值为1、方差为1的高斯分布；roundn为四舍五入函数；rand产生[0,1)均匀分布随机数。

在高斯变异过程中，产生的可能会超出区间范围。当它在维度上超出边界，通过式(4)的映射规则映射到可行区间的新位置。

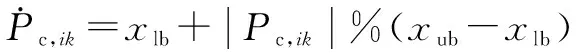
(4)

式中:、分别为交叉概率区间的上边界和下边界。

2.1.2 适应度函数改进

GA算法的适应度函数是基于路径长度和路径拐角奖惩机制进行评价的。路径长度计算公式如下：

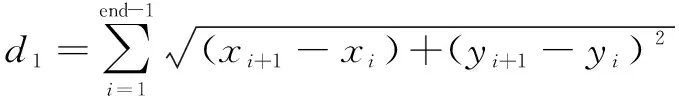
(5)

=1

(6)

式中:为连续路径的总长度。

为减少路径的拐弯个数，让路径尽量平滑，引入拐点奖惩机制，公式如式(7)所示：

(7)

=1

(8)

式中:为连续路径的奖惩点数。

适应度函数总的计算公式如下：

=+

(9)

根据路径长度和拐角奖惩点数选择合适的权重参数。

2.1.3 交叉方法

遗传算法的交叉操作流程如图3所示。

图3 交叉方法流程

2.1.4 变异方法

遗传算法的变异操作流程如图4所示。

图4 变异方法流程

2.2 HPACEA中蚁群算法的改进与链接

2.2.1 蚁群算法衔接设置

为了充分发挥GA算法的进化效果，减少算法的无用迭代,在GA算法和ACO算法融合处采用最小进化率参数评估是否由GA算法进入ACO算法。对GA算法设置一个最小迭代数和最大迭代数,当GA算法的进化率连续代小于给定的最小进化率时开始进入ACO算法。进化率计算方法如下：

=(--1)-1=2,3,…,

(10)

(11)

式中：为适应度评价值；为个体的进化率；为进化代数；为种群规模；RE为每一代的进化率。

当确定由GA算法进入ACO算法时，将GA算法最后一代得到的路径中排名前15%路径信息转化为HPACEA算法中的初始信息素分布。

=+

(12)

式中：为信息素常数；为由遗传算法得到的初始路径经过计算得到的信息素值。

2.2.2 蚁群算法信息因子和期望因子改进

HPACEA算法蚂蚁寻路时采用混合参数来提高蚁群寻路的多样性，即每次迭代都引入高斯变异产生新的和。∈(0,3),∈(0,7),其选择公式如下:

=roundn(((3-rand())·min(3,2+7)),-2)

(13)

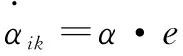
(14)

=roundn(7×rand()06,-2)

(15)

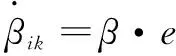
(16)

(17)

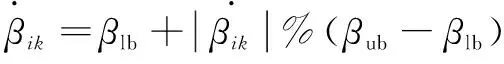
(18)

式中:、、、分别为、的上边界和下边界。

2.2.3 信息素更新方法

在每代蚁群寻路结束后，进行信息素更新时采用精化策略，其更新方式为

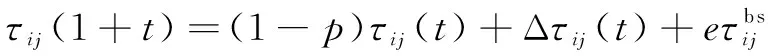
(19)

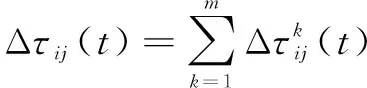
(20)

对信息素挥发因子采用一种自适应调整方式：

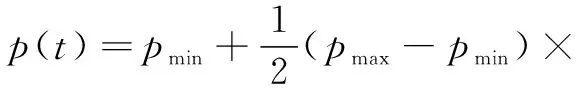
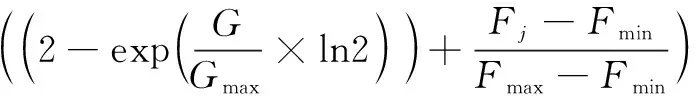
(21)

式中:为的最小值；为的最大值；为适应度最大值；为适应度最小值。

在ACO算法的最后再次引入遗传操作，当ACO算法每次迭代路径的进化率大于给定的时，根据轮盘赌的概率决定是否对当代产生的路径进行交叉操作或变异操作，这样HPACEA算法总体形成了一个类似闭环的算法机制。

2.3 HPACEA算法路径光滑处理

在HPACEA算法的最后阶段引入三次B样条曲线，实现机器人路径的相对光滑。为判断去除多余节点后新生成的路径是否经过障碍物区域，引入评价变量。的表达式为

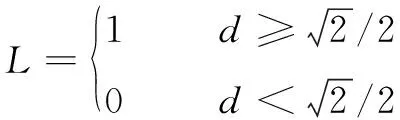
(22)

式中:为障碍物节点中心到新生成路径的距离。

平滑机制实施步骤：

(1)针对所有路径的节点，两两相连计算它们的斜率，若2个斜率不相同，则取它们共有的节点，放入节点集合中。

(2)把最优路径的起始节点和终止节点放入集合中，设={|=1,2，…，}，为起始点，为目标点。首先连接、，判断、连线是否经过障碍物，若=1;继续连接与下一节点，直到、连线穿过障碍物区域停止，则把、-1连接起来，删除它们中间的多余节点、…、-2，得到新的路径;从节点-1开始连接+1，依次判断每次连线是否经过障碍物。当集合中的节点都被连线过且新生路径中没有多余节点为止。

(3)对去除多余节点的新路径,采用准均匀B样条曲线对其进行优化处理。

图5展示了路线光滑过程中的3个路径阶段。

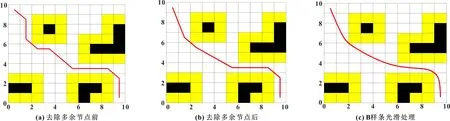
图5 光滑机制处理前后的路径

3 仿真实验验证

为证明HPACEA算法是有效可行的，采用MATLAB软件对栅格环境下的室内机器人进行路径规划仿真验证，和不同的算法进行验证比较。

3.1 20×20简单环境实验仿真

将HPACEA算法与传统的GA算法、ACO算法和文献[14]中GAAA算法在20×20的栅格地图进行仿真对比试验。HPACEA算法的初始条件为：遗传算法的迭代次数=50和=10，=3%，=50，=100，=100，∈[0,3]，∈[0,7]，(0)=07，=0.2,=1.8，设置起始点栅格序号为1，终止点为400。GA算法、ACO算法和GAAA算法，共有的参数设置和HPACEA相同，不相同参数按照经验自行设定。对比算法的具体参数设为：GA算法和ACO算法最大迭代次数为120,=0.8，=0.2，=1，=7。结果如图6、图7所示。

从图6可以看出:HPACEA算法获得的路径最短且相对光滑，ACO算法和GAAA算法次之，GA算法的运动轨迹最长且拐角最多。图7为4种算法的收敛曲线：GA算法的收敛速度最快，在迭代18次找到稳定解，但找到的路径经常属于次优解；HPACEA算法的收敛速度较快，在迭代20次即可找到最优解；GAAA算法和ACO算法都是50次迭代以后找到稳定解，并且找到的解经常不是最短路径。

图6 20×20环境中4种算法运动轨迹

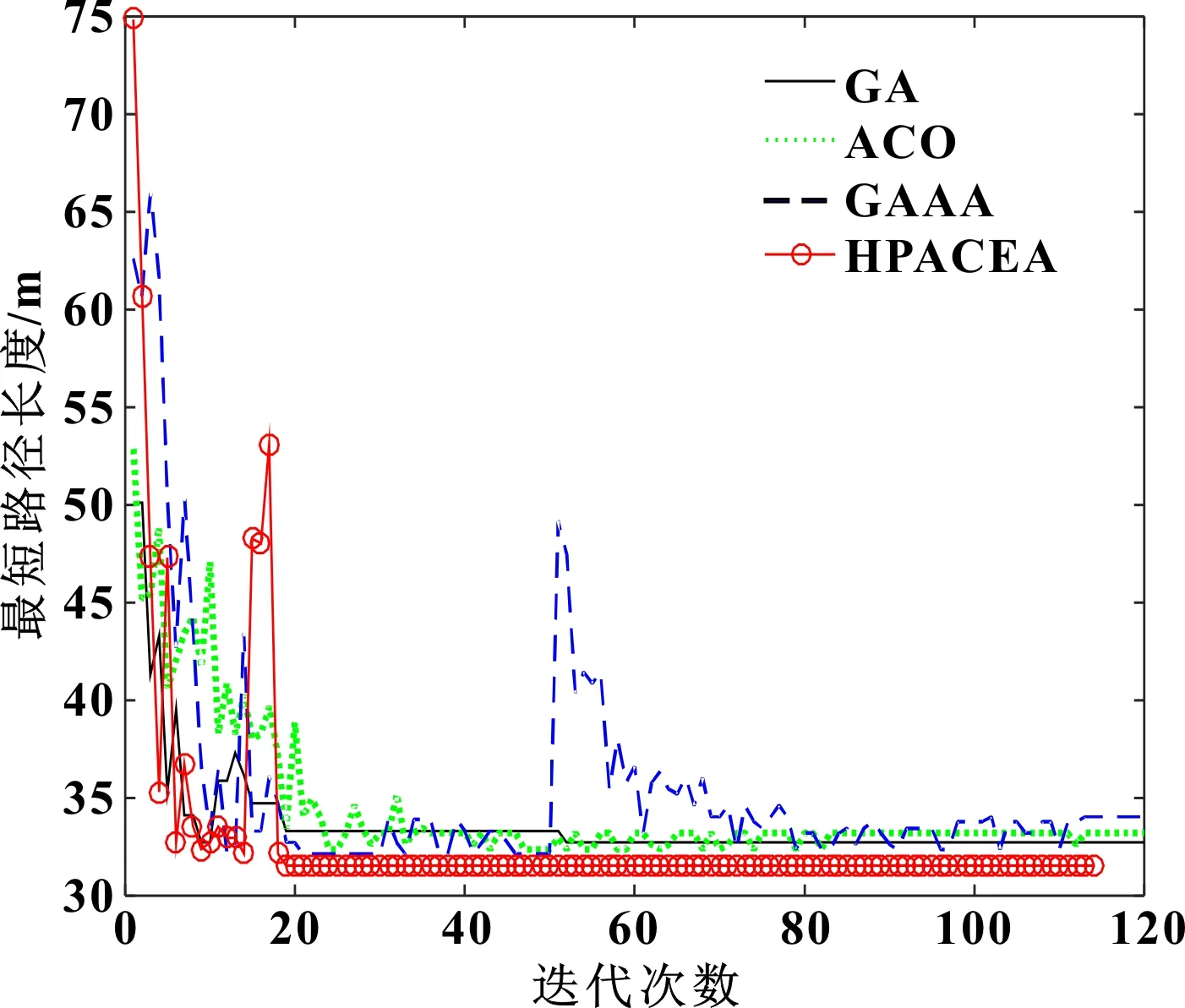
图7 20×20环境中4种算法的收敛曲线

表1是在20×20的栅格地图对4种算法进行10次路径规划的仿真实验数据，表中引入最佳寻优性能指标、时间性能指标和鲁棒性能指标作为路径规划算法的评价指标。可以看出：HPACEA算法找到的最优路径为29.49 m,相比其他算法找到的路径长度减少4.7%～9.8%，转弯节点减少45%～57%。从性能评价指标可以看出:GAAA算法和HPACEA算法的最佳寻优性能指标和鲁棒性能指标明显优于GA和ACO算法，其中HPACEA算法最好，GAAA算法次之；从时间性能指标上对比，GA算法收敛速度最快，HPACEA算法次之；从综合性能指标看出，HPACEA算法最优，综合性能明显比其他3种算法优秀。

表1 20×20环境中4种算法的仿真结果

3.2 30×30复杂环境实验仿真

采用30×30的复杂环境验证HPACEA算法的有效性，并与其他3种算法进行验证对比。实验结果如图8、图9所示。

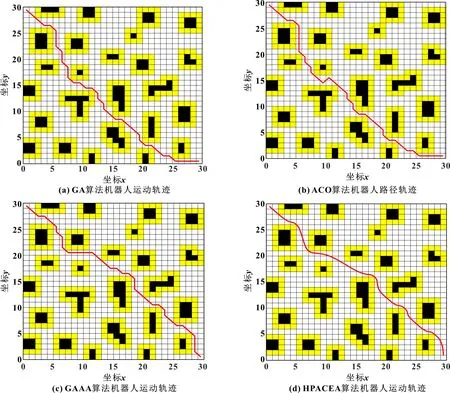
图8 30×30环境中4种算法运动轨迹

由图8知:传统GA、传统ACO和文献[14]的GAAA算法在面临复杂环境时，规划的路线存在许多转折点;而HPACEA算法加入光滑机制后，拐点数减少31%～40%，并且规划的路径更光滑。由表2知：最短路径长度是HPACEA算法找到的43.12 m,相比其他算法找到的路径长度减少6.8%～8%；文献[14]的GAAA和改进的HPACEA算法在鲁棒性能和最佳寻优性能指标上比较优秀，且HPACEA算法表现得最好。结合图9知:在复杂的环境里，传统GA算法和HPACEA算法达到稳定解的迭代速度是最快的，但HPACEA算法能找到更短的路径，且它的鲁棒性最好。HPACEA综合性能比其他3种算法更优秀，即使面对复杂的环境也能保持稳定性和快速寻找最优解的能力。

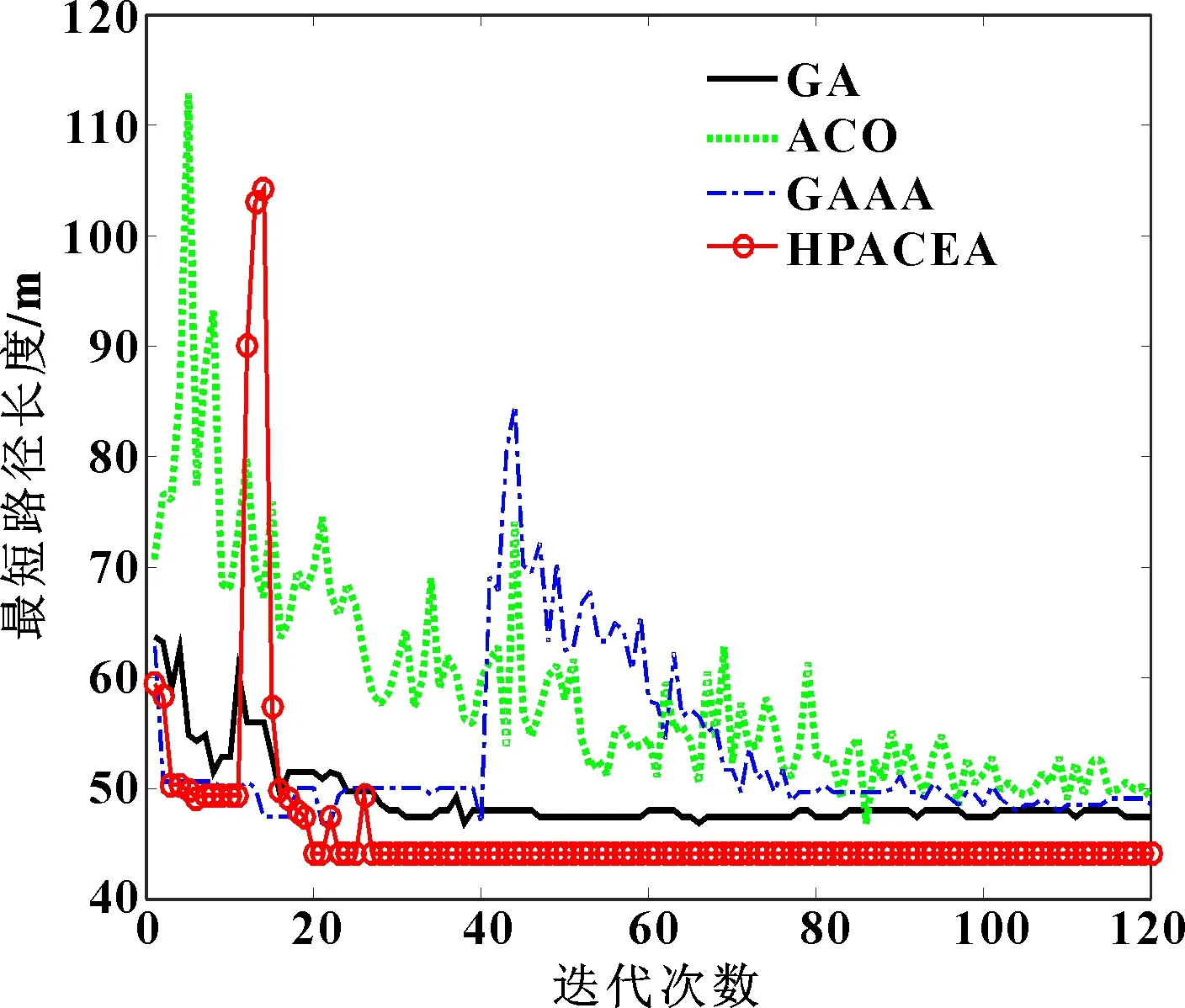
图9 30×30环境中4种算法的收敛曲线

表2 30×30环境中4种算法的仿真结果

通过设计2种不同室内环境，对传统GA算法、传统ACO算法、文献[14]的GAAA算法和改进HPACEA算法进行仿真实验，从算法的寻优能力、收敛速度和算法鲁棒性进行评估对比，验证了改进HPACEA算法在进行路径规划时具有较强的寻优能力、较快的搜索速度和求解稳定的特点，对复杂的环境也具有较强的适用性。

4 结论

(1)针对蚁群算法收敛速度慢和易陷入局部最优等缺陷，提出了混合参数的蚁群进化算法。该算法首先进行选择、交叉、变异操作，为下一步蚁群算法提供不同信息素信息;然后对蚁群算法的、、因子进行优化改进;最后对输出路径进行光滑加工处理。通过仿真实验证实了算法的可行性。

(2)在MATLAB中采用栅格法建立两种室内环境模型，将文中算法与其他3种算法进行仿真对比实验。结果表明：改进的算法在不同的环境下，找到的路径长度比其他3种算法减少了4.7%～8%，路径拐点减少了30%以上，且改进的算法可以较快找到一条相对光滑的路径，达到稳定解的迭代次数比ACO和GAAA算法减少了50%。