石材雕刻机械臂运动学性能的分析与优化

尹方辰，史宏伟，纪清智，陈寅昊，王柴志，黄国钦，崔长彩

(华侨大学制造工程研究院，福建厦门 361021)

0 前言

在石材产业中，石雕作为一门艺术，是石材与雕刻艺术的完美结合，一直记录着世界文明的发展历程，是人类文化及艺术传承的主要载体之一，具有较高的艺术价值和文化价值。立体石雕更是以其整体形状与轮廓构造复杂、曲面繁多等特点成为附加经济值较高的石材制品。在立体石雕产业中，加工是产业核心，立体石雕加工是离散制造形态，无法像鞋帽服装一样流水化生产，不能通过扩充设备数量、提高工人数量来降低单价成本，且产品的质量完全取决于专业工人的技术积累，因此新技术的引入是行业命脉。近年来，以机械臂为代表的智能加工装备，可以最大限度地代替人工劳动，降低人力成本，同时可以在各种复杂的环境中完成加工作业，在工件尺寸、加工效率与造型灵活性等方面已经表现出传统石材数控雕刻中心无法比拟的优势。在国内，厦门大学、山东大学与华侨大学等单位相继投入力量研发石材雕刻机械臂，在机械臂雕刻系统的总体设计、雕刻刀位轨迹生成与雕刻过程的仿真上取得了大量的研究成果。在国际上，ANDERSSON和JOHANSSON研究了机械臂雕刻过程中的力控方法，从而保证了机械臂雕刻过程的稳定性；HU和CHEN提出了一种机械臂雕刻复杂曲面的轨迹优化方法，为机械臂雕刻复杂曲面的轨迹设计提供了新的思路。

石材雕刻机械臂是六自由度串联机构，在其工作空间内运动性能的变化相当复杂，且立体石雕的工件毛坯尺寸通常较大，雕刻机械臂通常在较大的工作空间内进行加工，因而石材雕刻机械臂在其可达工作空间内运动性能的优劣直接影响立体石雕产品的加工质量。本文作者针对这一问题，对石材雕刻机械臂的运动性能进行分析与优化，并给出其最优工作空间的选取方法。为分析石材雕刻机械臂的运动性能，需要建立能描述石材雕刻机械臂运动性能的指标。机械臂雅克比速度矩阵具有奇异性，其求解逆矩阵精度较低，只可以定性地描述石材雕刻机械臂的运动性能。然而，石材雕刻机械臂的工作空间不仅要避开奇异区域，而且由于雕刻实际操作和控制精度的要求，工作空间应该尽量远离奇异区域。灵巧度是定量描述石材雕刻机械臂运动性能优劣的一个有效指标，它是指机器人沿任意方向运动并施加力和力矩的能力的难易程度。灵巧度越高，机械臂执行器末端越远离奇异点，可加工范围和控制精度都能显著提高，该指标在研究机械臂的连杆尺寸设计、轨迹规划和避障等问题时具有重要的指导作用。国内外许多研究机构对机械臂本体和机械臂加工系统进行了灵巧度分析及其加工空间优化。王伟和贠超优化了磨削机接触轮相对于机械臂基坐标系的位移偏移量，获得了机械臂砂带磨削系统具有最高灵巧度的磨削工作空间。郭肖鹏和张志利建立了排爆机械臂在工作空间内的灵巧度优化目标函数，并通过遗传算法对目标函数进行求解，实现了排爆机械臂灵巧度的优化。菅奕颖以工作空间与灵巧度为约束条件,对不同构形的六轴工业机械臂进行构形优化设计,对相同构形的机器人进行尺寸参数优化设计。肖华等人对一种六自由度压力容器检测机械臂的灵巧度进行仿真分析，并给出指定操作点的机械臂灵巧度仿真结果。对于石材的机械臂雕刻加工而言，如果石材工件毛坯能够摆放在合理的位置上，使得机械臂能够运动在其灵巧度最优的工作空间内，机械臂的运动性能与加工精度将得到显著提高。

本文作者基于D-H方法建立石材雕刻机械臂的运动学模型；提出一种适用于石材雕刻机械臂的灵巧度指标，并推导出它在工作空间内任意一点的计算方法；通过对石材雕刻机械臂加工轨迹进行仿真，分析机械臂在关节空间和操作空间坐标下灵巧度的变化规律。采用Dijkstra优化理论，以灵巧度最大为目标函数，在石材雕刻机械臂可达工作空间内，寻优得到其最优工作空间，并采用ADAMS仿真软件验证优化结果的有效性。

1 石材雕刻机械臂的运动学建模

1.1 D-H参数建模

本文作者所研究的石材雕刻机械臂如图1所示，其主体部分由德国库卡(KUKA)公司所生产的KR240-R2900高精度机械臂与意大利HSD公司生产的高速电主轴(30 kW,12 000 r/min)构成,并配备专用的石材雕刻刀具。由于石材雕刻机械臂中所有关节轴都是旋转副，使用D-H参数建立KR240-R2900机器人每个连杆的坐标系，如图2所示。此外，末端执行器的装载也会影响机械臂的运动学性能，为标定末端执行器参数与机械臂的负载参数，在图2中建立虚拟关节坐标系{}与腕关节坐标系{6}相连。根据图1所示的石材雕刻机械臂机械结构参数，确定石材雕刻机械臂各连杆D-H参数如表1所示。

图1 石材雕刻机械臂结构

图2 石材雕刻机械臂D-H参数坐标系

表1 石材雕刻机械臂D-H参数

-1、-1、和为连杆参数。其中，连杆长度是沿-1方向从-1轴到轴的距离；连杆扭角-1是绕-1轴从-1轴旋转到轴的转角；关节距离是沿方向从-1轴到轴的距离；关节转角是绕轴从-1轴旋转到轴的转角。

1.2 石材雕刻机械臂的正逆运动学建模

根据图2与表1,将所有的齐次变化矩阵相乘可得到石材雕刻机械臂末端位姿的变换矩阵。齐次变换矩阵已由D-H参数给出，因此正运动学方程可表示为

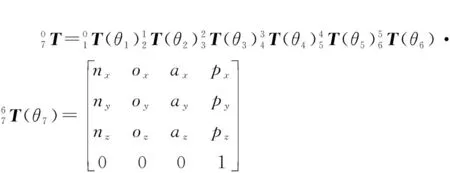
(1)

式中:[ ]表示变换矩阵中坐标系相对于轴的旋转向量，同理[ ]、[ ]分别表示变换矩阵中坐标系相对于、轴的旋转向量；[ ]表示机械臂末端刀具的位置向量。

根据每个坐标系的建立步骤，可将相邻坐标系变化的表达式描述为

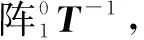
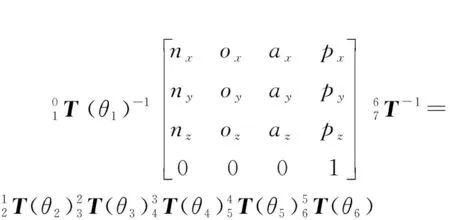
(2)

从等式(2)可以推导出下式：

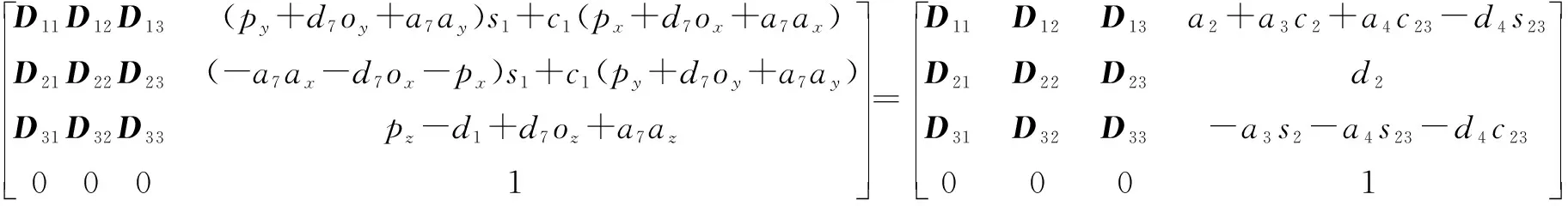
(3)

式中：为sin(+)；为cos(+);—为石材雕刻机械臂末端刀具姿态的矩阵。

令等式(3)左右两侧矩阵第二行第四列元素相等，得等式(4)如下：

(---)+(++)=

(4)

由等式(4)可得，关节角的逆运动学方程如下：

=arctan(++,++)-

arctan[,(-1)·

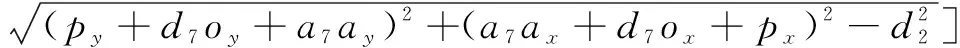
(5)

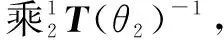
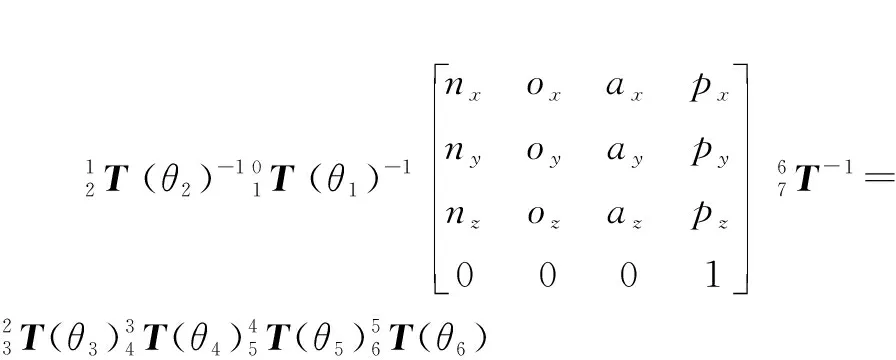
(6)

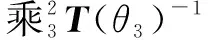
(7)

在等式(7)中只有3个未知量，因此求解等式(7)便可得到剩余的3个关节角、和的逆运动学方程。由建立的逆运动学方程可知，求解得到的石雕机械臂姿态解不是单一解而可能存在多个解。这表明当石材雕刻机械臂的末端执行器到达加工空间中的任意位置时，会存在不同的加工姿态。因此，石材雕刻机械臂能以不同的姿态到达同一个加工位置，并且其在不同的姿态下的运动性能也不相同。因此在实际的石材雕刻加工中，机械臂需要以具有最优运动性能的姿态来雕刻石材，以保证加工质量。

2 石材雕刻机械臂的灵巧度

在机械臂运动学中，机械臂雅克比矩阵反映了操作空间机械臂末端速度与关节空间的关节角速度之间的关系，如式(8)所示：

=()d

(8)

式中:()表示机器人的雅克比矩阵；表示末端执行器的速度。

对于文中所研究的石材雕刻机械臂，其雅克比矩阵为6×6阶方阵，当存在一组关节角度，使得雅克比矩阵行列式为0，此时机械臂有一个或者多个关节的轴线重合，机械臂就会丧失一到多个自由度。此时，末端执行器的坐标称为奇异点，奇异点的速度反解不存在，机械臂不具有可操作性，并且其运动性能指标都会变差。因此，在选择机械臂加工位姿时，应尽量远离奇异点。

机械臂的运动学性能指标是一个标量，用于衡量机械臂沿任意方向运动并施加力和力矩的能力。雅克比矩阵的条件数()的倒数可以作为运动性能指标来衡量机械臂末端执行器距离奇异点的距离，它被称为机械臂的灵巧度。其中，石材雕刻机械臂的雅克比矩阵条件数()可表示为

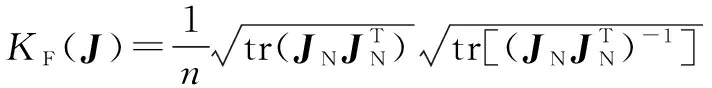
(9)

其中:tr()表示雅克比矩阵的迹；表示雅克比矩阵的维数。

则石材雕刻机械臂的灵巧度可表示为

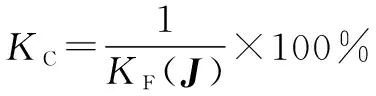
(10)

对于石材雕刻机械臂，为7。需要注意的是，这里的不是公式(8)中的雅克比矩阵()，而是雅克比矩阵的规范标准型。 规范标准类型的引入是为了解决雅克比矩阵的内部单位不一致的问题，其定义为

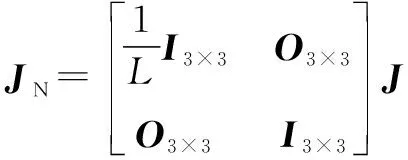
(11)

其中:、、分别是3×3的单位矩阵、3×3的零矩阵和雅克比矩阵。

特征长度的定义：确保雅克比矩阵的所有元素都有相同物理单位的归一化长度，计算公式为

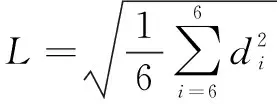
(12)

当条件数()为最小值时，石材雕刻机械臂的特征长度为一个关节点的转轴与末端点的转轴之间距离的均方根值。为获得石材雕刻机械臂的特征长度，建立目标函数如下：

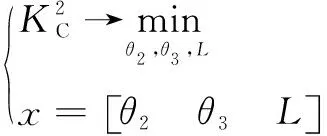
(13)

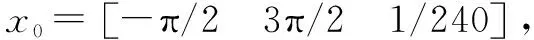
=-1.314 rad= 2.127 rad= 233.14 mm

根据公式(10)与式(11)可知，0<()≤1。当()=1时，雅克比矩阵的所有奇异值都相等，其对应的石雕机械臂运动性能最好。相反，当()趋于0时，雅克比矩阵的最小奇异值趋于零或者最大奇异值趋于无穷大。此时，末端执行器接近奇异点，其对应的石雕机械臂运动性能会显著降低。因此，为使石雕机械臂具有良好的运动性能，理论上应尽可能选择在()值大的区域运动。

3 石材雕刻机械臂运动性能分析

在使用石材雕刻机械臂进行雕刻加工时，常用走刀轨迹有回字形轨迹和工字型轨迹两种。文中以回字形走刀轨迹为例，在雕刻机械臂的可达工作空间内，对其进行运动学性能分析。在石材雕刻机械臂加工路径的离线仿真中，设定末端刀具姿态垂直于工件表面，在机器人末端刀具的姿态(，，，，，)中，只有、两个方向会随着加工路径而发生变化,如图3所示。将机器人操作空间坐标系的原点定义为，当石材雕刻机械臂在-平面上以不同的高度进行加工时，根据上文所提出的灵巧度指标()，可以获得石材雕刻机械臂在其可达工作空间内的运动学性能的分布。

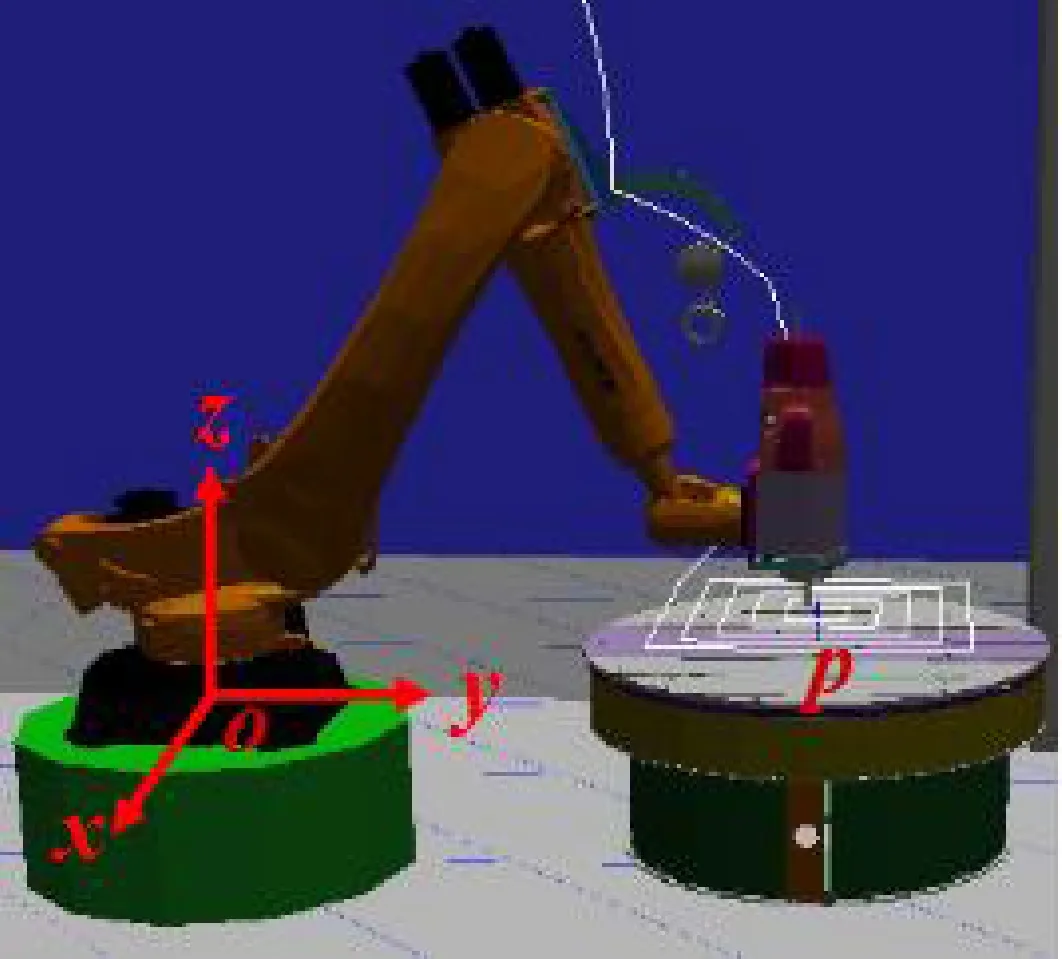
图3 石材雕刻机械臂加工空间区域示意

3.1 关节空间下的运动性能分析

如图3所示，工作台中心的坐标为(0,2 000,0)，轴的加工范围为-500～500 mm，轴的加工范围为1 500～2 500 mm。将轨迹位移每100 mm定义为一个单位步距，在石雕机械臂走回字形轨迹的过程中，轨迹的步数与-平面轨迹之间存在如下关系：

(14)

在石雕机械臂走回字形轨迹过程中，、和轴仅有微小变化，而机械臂轴不影响其加工性能，和轴主要影响机械臂末端位置的变化。因此,为分析石雕机械臂在其关节空间下的运动学性能，设定、、和为常数，通过改变和来分析石雕机械臂在关节空间内运动学性能的变化规律。变量条件设置如下：

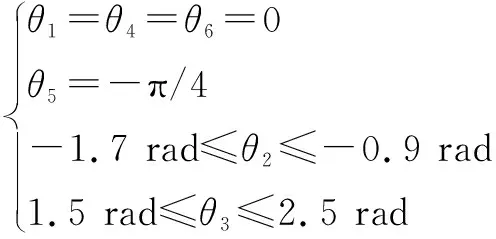
(15)

石雕机械臂在操作空间内和轴可达角度范围分别为[-1.7 rad,-0.9 rad]和[1.5 rad,2.5 rad]。在关节空间内计算得出石雕机械臂运动学性能随和轴角度变化分布，如图4(a)所示。在第1.1节机械臂D-H参数建模中提到，机械臂末端执行器的质量也会影响其运动学性能。因此，本文作者以相同的角度约束条件分析石雕机械臂在未装载末端执行器情况下的关节空间运动性能分布情况，结果如图4(b)所示，与装载电主轴情况下的机械臂运动性能进行比较。

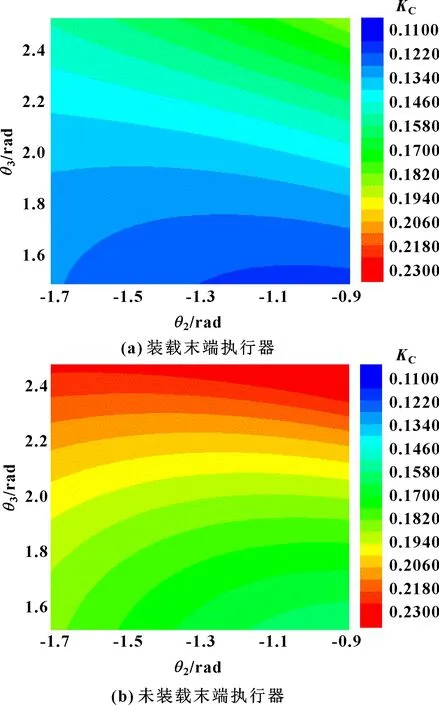
图4 石雕机械臂在关节空间下的运动性能图谱

由图4可知：石雕机械臂未装载末端执行器时灵巧度指标在0.16～0.24范围内分布，装载末端执行器时灵巧度指标在0.12～0.19范围内分布，两者具有类似的变化趋势。末端执行器的装载降低了机械臂的灵巧性能，石雕机械臂整体运动性能下降。同时，石雕机械臂在其工作空间内，其运动性能随着和的增大逐渐增强。因此，在末端轨迹点不变的条件下，石雕机械臂应该选择和角度较大的姿态进行加工。

3.2 操作空间下的运动性能分析

石雕机械臂在实际雕刻加工中，逐层向下走回字形轨迹，在操作空间中可视为在不同方向高度上进行加工。为研究石雕机械臂在操作空间下运动性能分布，将-平面中的工作区域按每100 mm分成11×11=121个步数点,计算出石雕机械臂在不同高度下，每个步数点位置下的灵巧度指标()，拟合得出灵巧度的等高线，即运动性能图谱，如图5所示。

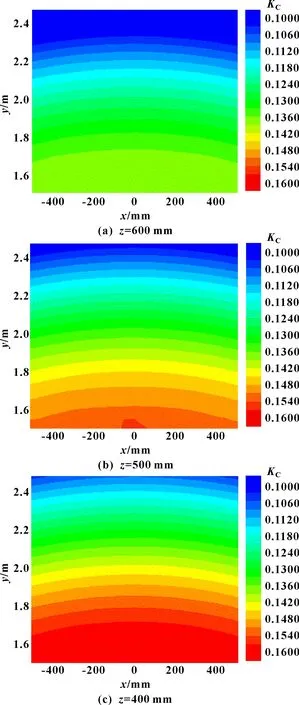
图5 不同高度z下的x-y截面运动性能图谱

由图5可以看出:在方向不同高度上，石材雕刻机械臂的运动性能分布均关于轴对称。这是由于石雕机械臂轴的变化不会影响机械臂的运动性能，且灵巧度指标是以同心圆形状向外扩散，而不是以平行线形式递减，同样验证了第3.1节中所述的轴不会影响机械臂的运动性能的假设。同时，在相同的方向高度上，随着方向的位移不断增加，即机械臂不断向外延伸加工，其运动性能逐渐降低。当加工高度为600 mm时，石雕机械臂在-截面上灵巧度分布范围为0.087～0.139，在=500 mm和=400 mm高度下灵巧度分布范围分别为0.096～0.156、0.104～0.162。可以发现，随着雕刻过程的进行，即末端执行器垂直工件表面向下运动时，石雕机械臂在不同高度下时，-截面的整体运动性能也随之逐渐增强。

进一步地，选取二维空间平面-，其中轴范围是-500～500 mm，轴范围是100～1 100 mm，方向选取1 500、2 000、2 500 mm 3个位置，以同样的加工姿态，分析在方向不同位置上-截面石雕机械臂运动性能分布情况，如图6所示。

图6 y方向不同位置处x-z截面运动性能图谱

由图6可知：在方向不同位置处，石雕机械臂的运动性能均随着高度的减小而增强；当=1 500 mm时，机器人在-截面上灵巧度分布范围为0.076～0.175；当=2 000 mm和=2 500 mm时，-截面上石雕机械臂灵巧度分布范围分别为0.053～0.160、0.027～0.126。可以发现，随着石雕机械臂向外伸展加工，它在方向不同位置处-截面的整体运动性能随之逐渐减弱。

4 基于Dijkstra优化理论的石雕机械臂工作空间优化

一般石雕工件毛坯多为规则几何体形状，而毛坯位置的摆放大多遵循人为经验选择，对毛坯工件的摆放尚未有理论的指导依据。根据前文的分析可知，石雕机械臂在不同的关节空间与操作空间下，其运动性能有很大差别。因此，需要对石雕机械臂的固有灵活工作空间进行优化，使得机械臂的作业对象完全布局在该优化空间内，这样石雕机械臂在进行雕刻加工时，才会具有更好的运动性能。文中所研究的石材雕刻机械臂的可达工作空间为工作台中心上方1 000 mm×1 000 mm×1 000 mm的立方体空间区域。石材雕刻机械臂在其可达工作空间中的灵巧度分布如图7所示。其中，预设的工件毛坯尺寸为500 mm×500 mm×500 mm，以其灵巧度最大的加工区域为优化目标进行优化。

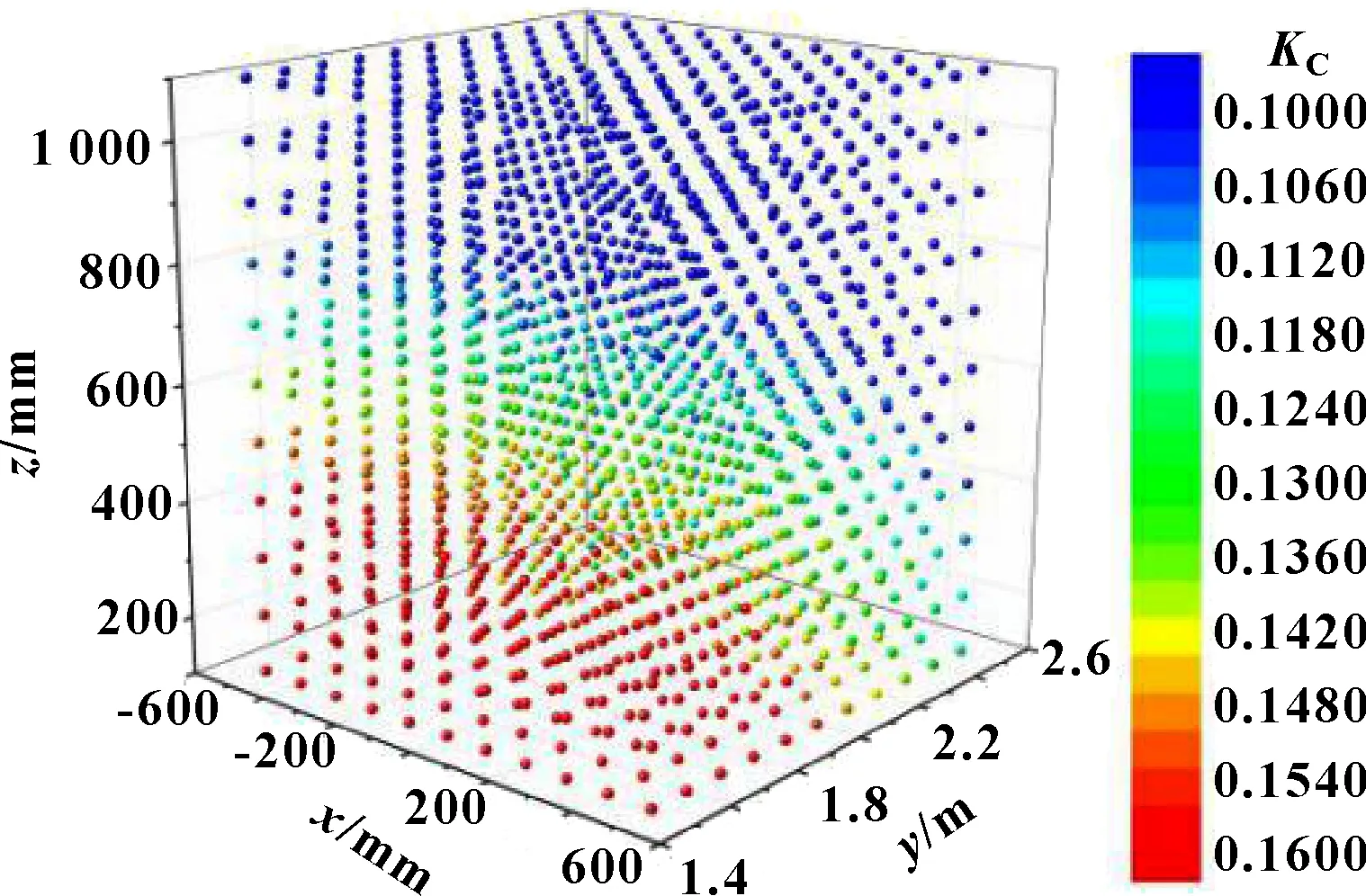
图7 石材雕刻机械臂在工作空间下的运动性能图

4.1 基于Dijkstra理论的优化过程

Dijkstra优化理论是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径，其主要特点是以起始点为中心向外逐层扩展，直到扩展到终点为止，其搜索优化过程如图8所示。在图8中，通过建立的二维数组(见图9) 将具有某种关系的任何两个顶点连接在一起。数组dis表示起点和其他点之间的距离，其初始值为[0，2，6，4]。数组簿表示是否数组dis所对应的距离是最短，其初始值为[1，0，0，0]。Dijkstra优化理论的目的是获得起点与其他点之间的距离，选择距离点1最近的点2作为下一个搜索点。在图9所示的二维数组中，所有项都是正数，如果选择另一个点作为下一个搜索点，则距离一定会比点2和点1之间的距离更长。数组簿更新为[1，1，0，0]，然后检查是否存在通过点2到达起点1的任何其他点间的距离短于点2与点1之间的距离。可以发现，dis[3]=6，dis[2]+edge[2][3]=5<6，dis更新为[0，2，5，4]。重复上述更新过程，可以在每次迭代计算后获得中间点和起点之间的距离。因此，最多执行3次更新过程，便可得到优化结果。

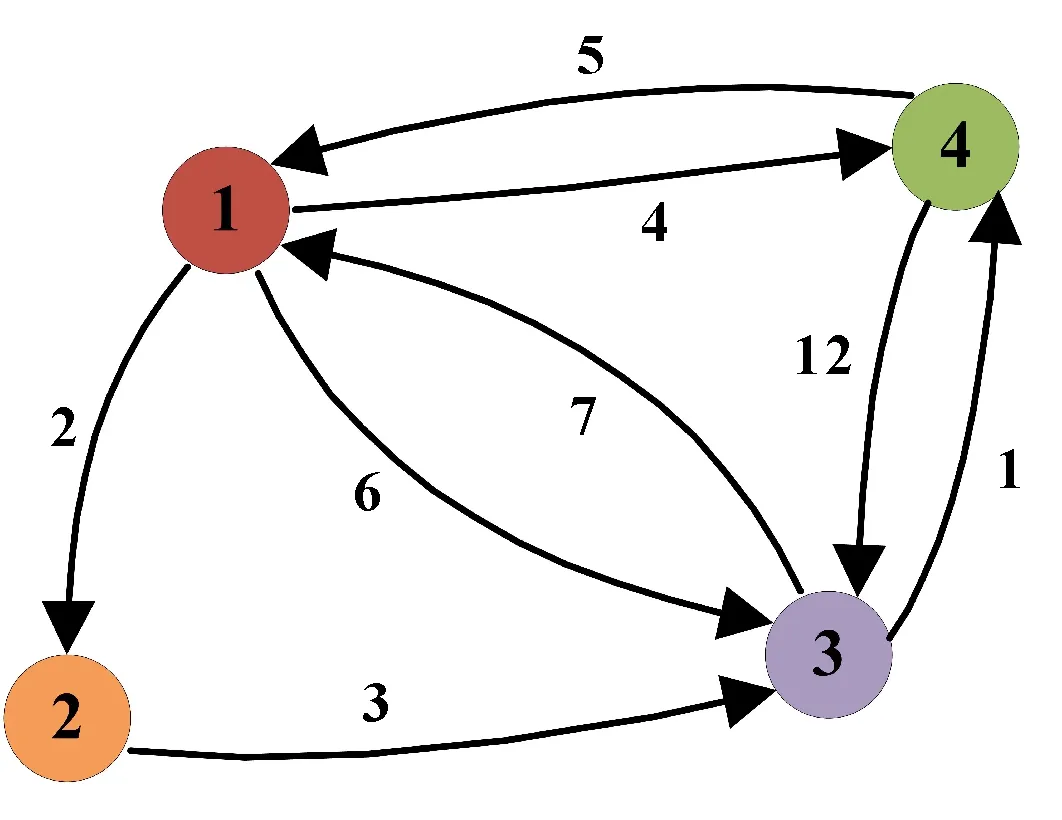
图8 Dijkstra优化理论的搜索优化过程示意

图9 Dijkstra优化理论中的数组

为在石材雕刻机械臂可达工作空间内，寻优得到运动性能最优的工作空间，设计Dijkstra优化理论的执行流程如图10所示。

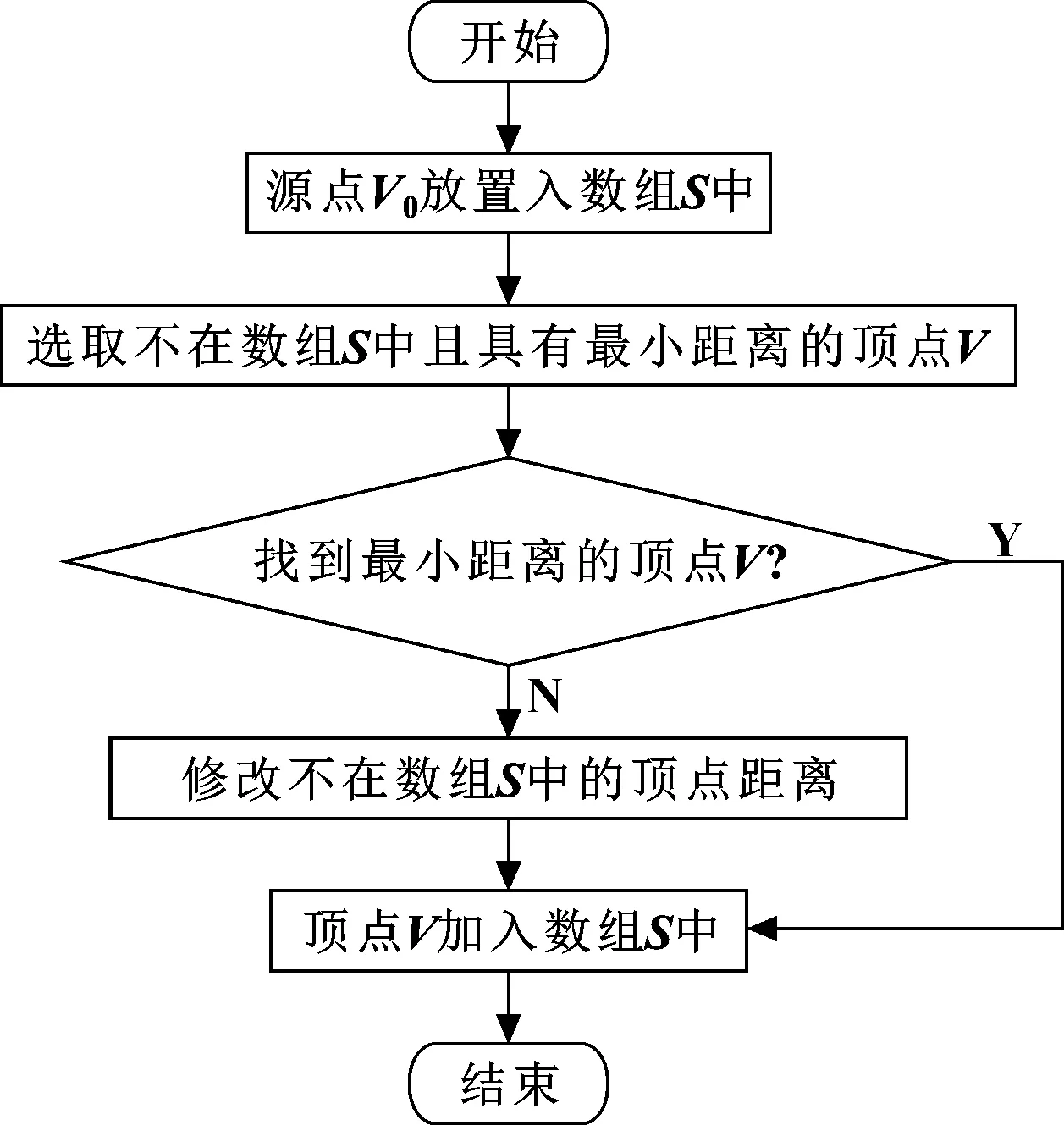
图10 Dijkstra优化理论的执行流程

步骤1，初始时，数组只包含源点，即={}，与其他顶点的距离为0。数组包含除外的其他顶点，即={其余顶点}，若与中顶点有共边，则<,>正常有权值，若不是的共边邻接点，则<,>权值为∞;

步骤2，从数组中选取一个距离最近的顶点，把加入中(该选定的距离就是到的最短路径长度);

步骤3，以为新考虑的中间点，修改中各顶点的距离；若从源点到顶点的距离(经过顶点)比原距离(不经过顶点)短，则修改顶点的距离；

步骤4，重复步骤(2)和(3)，直到所有顶点都包含在数组中。

根据上述设计步骤，将石材毛坯内216个步数点的灵巧度逐步累加求和得到区域灵巧度，经过寻优得到值最大的区域即为目标加工区域。经过寻优计算得到，石材雕刻机械臂在其可达工作空间内灵巧度最大的5个点分别为(500,1 500,100)、(400,1 500,100)、(300,1 600,100)、(0,1 600,100)、(0,1 600,100)，其灵巧度分别为0.174 57、0.174 53、0.174 51、0.174 50、0.174 45。将这5个点 (=1,2,3,4,5)作为源点，可达空间内其余1 326个点作为数组；选取中相对中灵巧度两者差值最小的点加入中，以此类推，将每个源点逐渐扩展至与预优化空间几何形状和大小相同的点集，计算每个的值。经过计算，石材毛坯内216个步数点，最大灵巧性值=33.475 65，位于∈[-300 mm,200 mm]、∈[1 500 mm,2 000 mm]、∈[100 mm,600 mm]的几何区域，如图11所示。

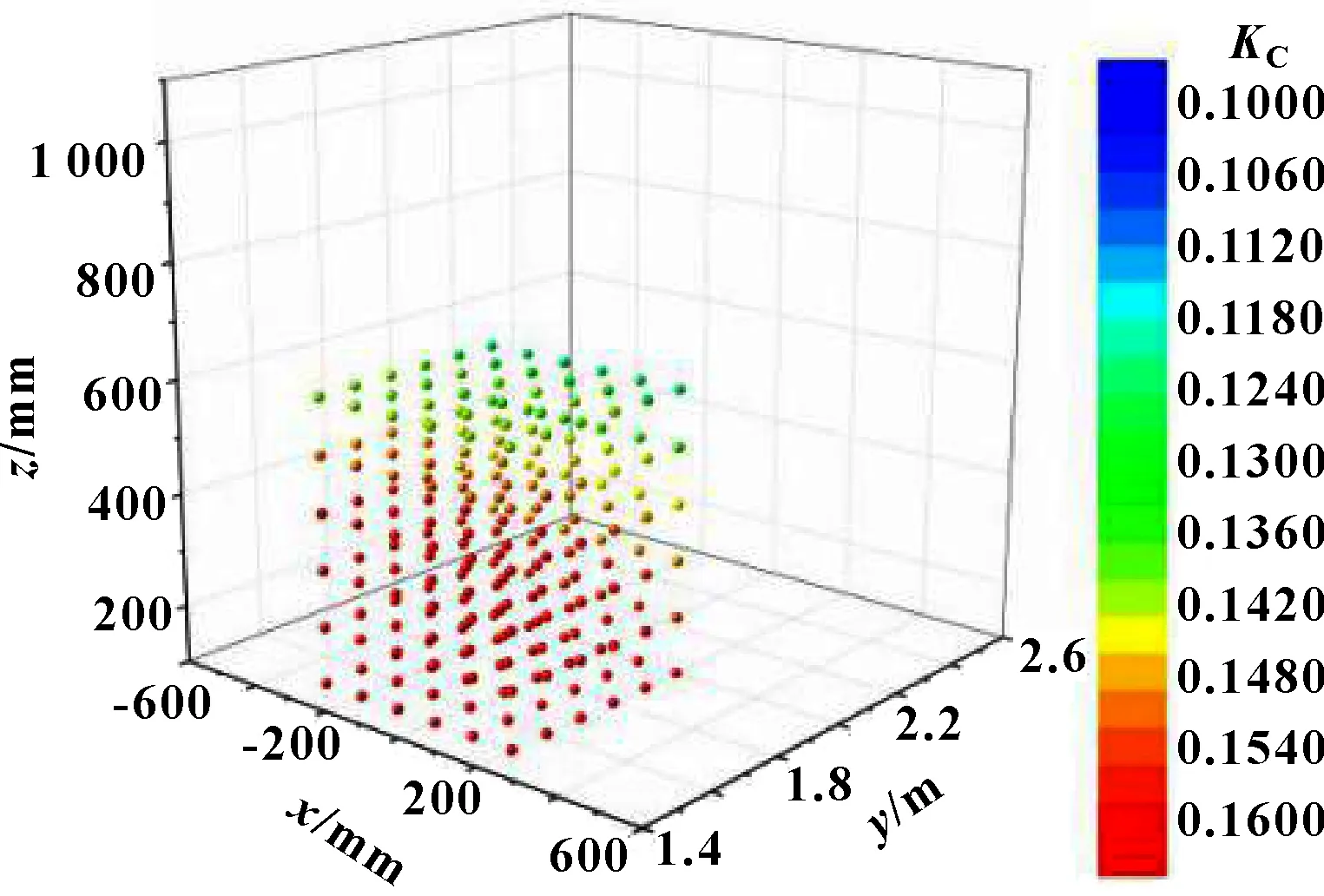
图11 石材雕刻机械臂最优工作空间

4.2 优化结果验证

石材雕刻机械臂是一个复杂的非线性系统，每个关节都会相互作用，因此很难直接在ADAMS软件中建立其3D模型。为验证优化结果的正确性，在3D设计软件SolidWorks中建立KR240-R2900机械臂模型和HSD末端执行器模型，并将所建立的模型以特定格式导入到ADAMS中。最后，建立一个可正确表征雕刻机械臂在石材雕刻过程中运动性能的动态模型。模型建立的具体过程如下：

(1)石材雕刻机械臂模型装配

末端执行器的实物如图12(a)所示，根据实际尺寸，在SolidWorks中设计的末端执行器的三维模型如图12(b)所示。将机械臂主体与设计的末端执行器装配在一起，如图13所示，将装配配合约束添加到石雕机械臂的相邻组件中(机械臂基座，腰关节，大臂关节，小臂关节，肘关节和末端执行器)。为使石雕机械臂装配模型可导入ADAMS中，在SolidWorks中将其模型保存为parasolid (*.x_t)格式。

图12 石雕机械臂末端执行器模型

图13 石材雕刻机械臂的装配模型

(2)ADAMS中的仿真参数设置

①仿真环境设置

HSD末端执行器是由45钢制成。经过多次相关标定试验后，将末端执行器的材料密度设为7.801×10kg/mm，将其弹性模量设为2.07×10N/mm，泊松比设为0.29。然后，基于建立的装配模型，计算其各组成部分的动态特性参数，并对各关节进行校正试验，表2所示为石材雕刻机械臂的最终动态特性参数。该表包含了仿真所用到的石材雕刻机械臂每个连杆质量、质心与惯性矩的信息。

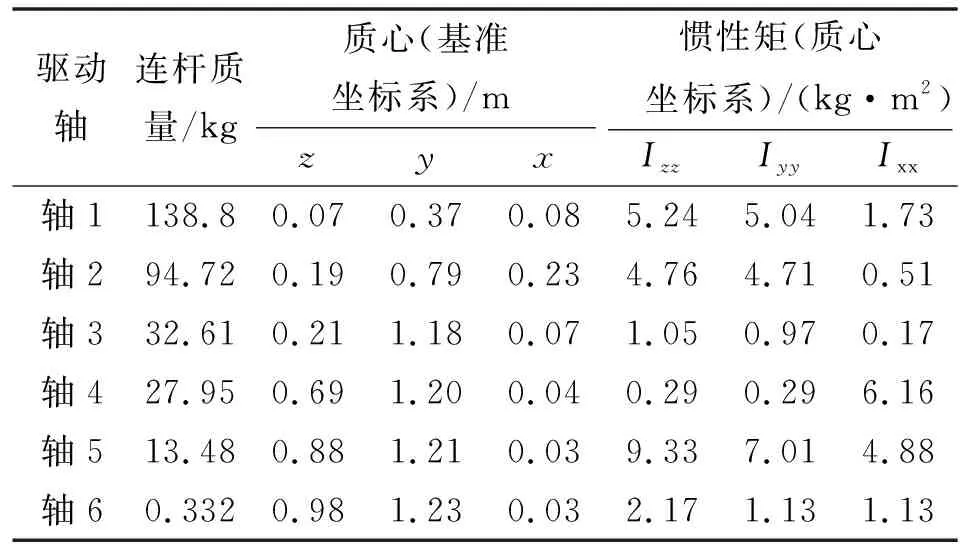
表2 石材雕刻机械臂组成部分的动态特性参数

②关节驱动设置

石雕机械臂基座和大地坐标之间的关系是固定的，关节6和末端执行器之间的关系也是固定的，因此将它们的关节连接方法设置为固定副。此外，相邻关节 (轴1，轴2，轴3，轴4，轴5，轴6) 之间存在偏转运动，将它们的关节连接方法设置为旋转副。然后，创建石雕机械臂每个关节的角度函数作为用于驱动设置的各关节驱动函数。将前文中的角度函数导入ADAMS软件中，以创建位于数据单元中的SPLINE函数。最后，配合使用SPLINE函数与ADAMS中内置的“Cubic Fitting Method”就可以驱动石材雕刻机械臂运动。

③仿真与测量

设置好驱动函数和仿真时间(12 s)后，可以在ADAMS中模拟石材雕刻机械臂的运动过程。根据实际要求，测量石雕机械臂每个关节的角速度和角加速度，并在后处理窗口中获得每个关节的测量变化曲线。在该窗口中，可以导出测量变化曲线，也可以将外部数据导入到ADAMS中，从而实现不同变化曲线的比较。在3个不同加工位置，石材雕刻机械臂均以相同回字形轨迹和2 000 mm/min的进给速度运动，如图14所示。按照文中所提到的方法，计算不同加工位置(No.1、No.2和No.3)的总灵巧度，结果如表3所示。位置1 (No.1)是通过Dijkstra理论优化的加工位置，位置2(No.2)和位置3(No.3)是石雕机械臂可达空间中选取的任意加工位置。在3个位置(No.1、No.2和No.3)、6个关节角速度～和角加速度～的变化曲线分别如图15和图16所示。方差值～、～分别如表4、表5所示。

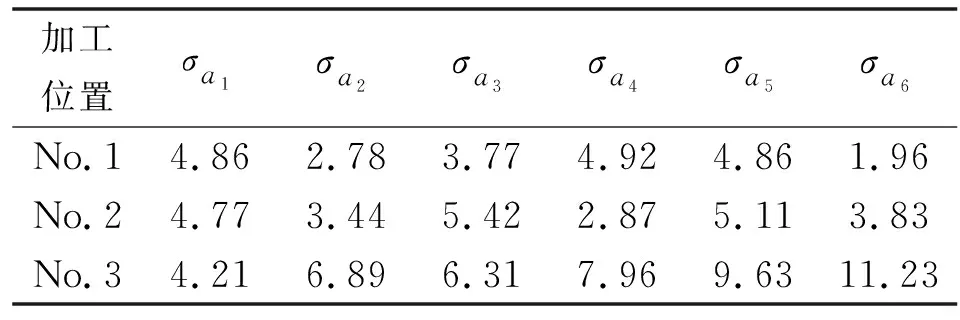
表5 不同加工位置的角加速度性能对比

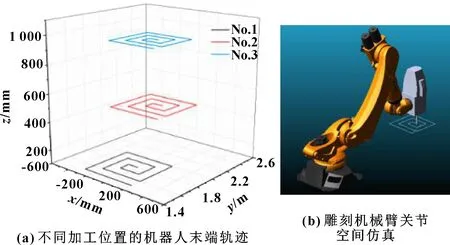
图14 石材雕刻机械臂雕刻过程仿真

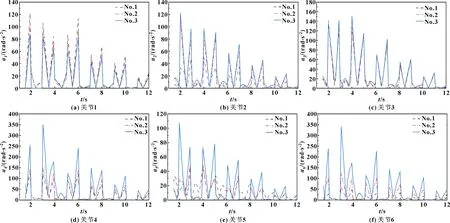
图16 石雕机械臂各关节角加速度的变化曲线

表3 不同加工位置的灵巧度对比

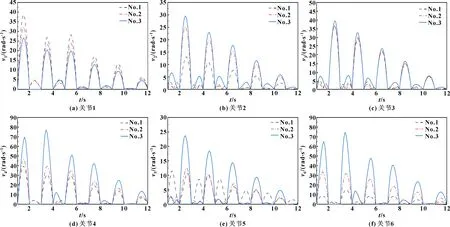
图15 石雕机械臂各关节角速度的变化曲线

如图15和表4所示：除石雕机械臂关节1外，其他关节位置No.1处的速度最大值与方差值均明显小于加工位置No.2与No.3,且随着灵巧度指数的增加，石雕机械臂的运动性能变强。以最影响石雕机械臂运动性能的关节2为例，在机械臂运动性能最优的位置No.1处进行加工，相比于位置No.3处，角速度方差减少了60.6%。各关节角速度方差的减少，不仅可以提高石雕机械臂的作业效率，同时也可以降低加工时的能量消耗。

表4 不同加工位置的角速度方差

如图16和表5所示：石雕机械臂在最优加工位置No.1处运动时，除了关节1外，其他关节的角加速度方差也均明显小于加工位置No.2与No.3，进一步验证了优化结果的有效性。在位置No.1处运动时，关节2的角加速度方差仅为2.78，比它在位置No.3处运动时减少了59.6%；在位置 No.1 处，关节3的角加速度方差仅为3.77，比它在位置No.3处运动时减少了40.2%。各关节角加速度方差的减少，不仅可以提高石雕机械臂的运动脉冲，也可以减少加工中的冲击，有利于提高跟踪精度，保护机械结构。

5 结论

(1) 基于D-H参数法建立了所研究的石材雕刻机械臂的运动学模型，并通过旋量理论中的指数乘积公式推导出了石材雕刻机械臂正运动学解和逆运动学解。

(2) 基于雅克比矩阵的条件数，提出了一种可以定量描述石材雕刻机械臂运动性能的指标(灵巧度)，并进一步研究了灵巧度指标在关节空间坐标和操作空间坐标下的变化规律。结果表明：随着石雕机械臂不断向外延伸(方向位移增加)，其运动性能会降低，且在其可达空间内，-横截面的整体运动性能随着雕刻加工的进行(即高度逐渐减小)而提升。

(3) 基于Dijkstra优化理论，设计了石材雕刻机械臂最优工作空间的优化目标与优化流程。仿真结果表明：当石材雕刻机械臂在其最优工作空间中工作时，其关节角速度的波动会减少60.6%，关节角加速度的波动会减少40.2%。证明了文中算法的有效性，可为石材雕刻机械臂加工位置的布局提供参考。