Delta并联机器人机构多目标优化设计
孔凡国,李肇星,柯子旭
(五邑大学智能制造学部,广东江门 529000)
0 前言
Delta系列机器人的工业需求日益增大,使其研究与应用呈现轻量化、高速、高精度、高灵活性等趋势。由于设计时要同时考虑的各项性能指标数量较多,基于Pareto 排序的传统算法在处理目标数为4个或以上的问题时(即高维目标)效果并不理想,并且会产生较高的计算费用。
文献[2]基于雅克比矩阵,对机器人运动性能的影响因素进行了研究,并分析了工作空间的主要影响因素。文献[3]针对三自由度Delta机器人控制精度问题进行研究,详细分析了机器人各结构误差源对控制精度的影响。文献[4]对三自由度 Delta 并联机构的设计空间、空间点位置及雅克比矩阵条件数3个目标建立惩罚函数,并采用遗传算法进行尺度综合。文献[5]研究了三自由度Delta并联机构的运动学和定向能力,定向能力与尺寸参数之间的关系表明,尺寸参数不会影响奇异位置运动的输出运动特性。文献[6]根据工作空间、速度、加速度和惯性力的要求,建立了4个目标函数,选取NSGA-2 算法,基于iSIGHT平台DOE方法,对3-PUU并联机构进行了多目标优化设计,最终得到了Pareto解集。
本文作者针对运动学、动力学的多个目标,考虑机构关节的影响,选取合理的优化策略,在满足性能要求的基础上对机械结构进行尺度综合,在控制计算费用的同时,使机器人具有良好的性能。
1 Delta并联机构
以3-DOF Delta机器人为例,对如图1(a)所示的三维模型进行抽象与简化,建立其机构简图,如图1(b)所示。将静、动平台简化为2个等边三角形,外接圆半径分别为、。以静平台中心为原点建立静坐标系-,以动平台中心′为原点建立动坐标系′-′′′;两坐标系轴均为竖直向上,轴指向中点,轴指向中点。
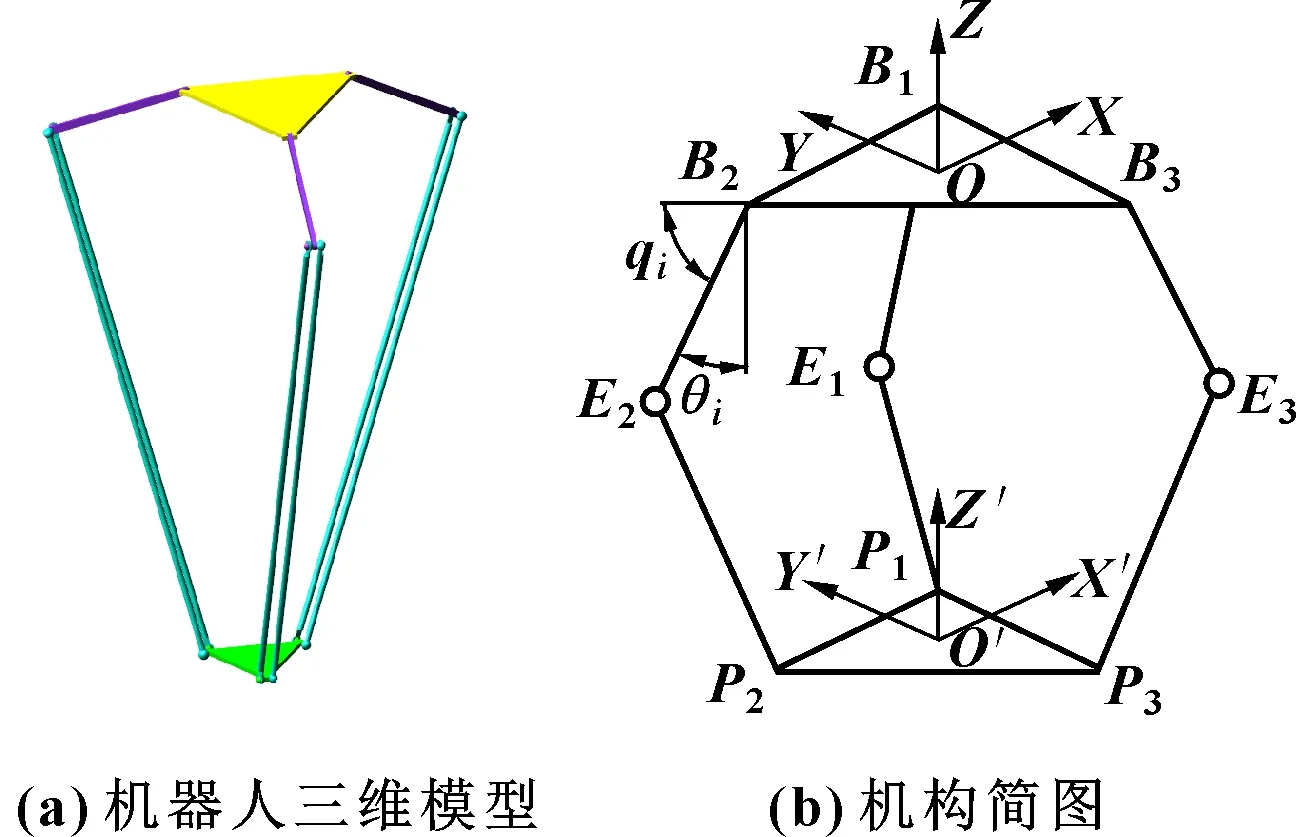
图1 Delta机器人模型及机构简图
设为各主动臂长度,为各从动杆长度,为从动杆直径,为主动臂与静平台轴锐角夹角,(=1,2,3)为各驱动关节的驱动角度。
2 动力学模型
计算闭链机构动力学模型的经典方法:考虑等效树结构,使用Lagrange乘数或D′ Alembert原理实现运动学约束。
常用动力学建模方法包括虚功原理法、拉格朗日法、密哈尔顿原理法和牛顿-欧拉法。其中,建立牛顿动力学方程需要分析质点系的约束力,消去非独立坐标,然后消去未知的约束力,以求得一个尽可能简单的微分方程组。
对于并联机构而言,动力学模型通常比较复杂不易求解,且坐标间的耦合程度会影响其运动性能和控制性能,因此需对模型进行简化以消除杆件之间的耦合。将从动杆的质量惯量分为2份,1份分给主动臂,1份分给动平台。将从动杆的惯量分为3份,2份分配给主动臂,1份分配给动平台。由虚功原理可知系统受力包括动平台受力和主动臂受力,所有非惯性力之和等于惯性力。如图2所示,动平台仅平动,受到自身重力和惯性力的影响;主动臂仅转动,受到自身重力、电机转矩和主动臂自身转动惯量的影响。

图2 Delta机器人系统受力树状图
简化后动平台等效平动惯量及等效惯性质量分别表示为

(1)

(2)
式中:为动平台质量;为动平台负载质量;为从动杆质量。
简化后主动臂等效质量为

(3)
式中:为主动臂质量;为主动臂上的球铰质量。
模型简化后,主动臂惯性质量的质心位置为

(4)
主动臂重力等效转矩为
=···[cos]
(5)
主动臂总转动惯量b为输出轴转动惯量与主动臂自身转动惯量的和:
b=+=1,2,3
(6)
=(+)
(7)

(8)
式中:为电机转动惯量;为减速器转动惯量;为减速器减速比。
令主动臂等效转动惯量为

(9)
由虚功原理可得Delta并联机构逆动力学方程为

(10)

(11)
3 优化策略
对于低速并联机构,仅考虑工作空间、雅克比条件数、奇异值等基本动力学指标即可得到较好的优化结果。上述指标可经基本代换变为单目标问题解决,优化过程较简单。
由于机械手不停向高速度、高精度方面发展,机械手的设计优化既要满足运动学要求,还需有良好的动态特性。对于运动构件的惯量、逆动力学方程中坐标间的耦合程度以及驱动机构运动所需的驱动力矩与驱动功率等性能指标,要建立准确的动力学方程进行优化。
考虑到机构所处的位形不同,杆件的长度、截面积不同均会影响上述指标,高速并联机构的优化问题常常较为复杂。
本文作者以非支配排序遗传算法NSGA-II 对Delta并联机器人结构尺寸进行优化。优化策略:进行试验设计,依据试验结果规定设计变量及其取值范围;选取试验结果中趋势相似的响应变量,整合后建立新的目标函数;在加以约束的情况下,借助NSGA-II完成机构运动学、动力学多目标尺度综合。
3.1 设计变量
为研究多因子与响应变量之间的关系,进行试验设计。选取最优拉丁超立方试验设计方法获得数据样本,设置样本为1 000组,令为局部刚度,为局部动力学灵巧度,+为驱动力矩和功率的和,为最小奇异值,为可操作度,得出自变量、、、、与响应变量的关联度如表1所示。

表1 因子与响应变量的关联度
假设各杆截面形状规则,杆质量与杆长、截面尺寸成正比关系,依据试验结果选取动平台半径、静平台半径、驱动臂长度、从动杆长度、从动杆直径作为设计变量,以使机械手在给定范围的工作空间中整体尺寸最小。
3.2 优化目标
由于具有高维目标的最优解求解时不易收敛,且可视化较差,所以本文作者将Delta并联机构运动学、动力学的常见性能指标综合为3个优化目标。所涉及到的指标包括:可操作度、全局刚度、全局动力学灵巧度、功率及力矩、雅克比全局条件数。
3.2.1 运动学目标
在机械手的优化设计中,由于可达工作空间的体积并不能成为评价机器人在工作空间中的整体运动学性能的唯一判据,需引入其他性能指标。对于一个并联机构,其灵巧度可以用来反映输入输出运动或力之间的传递精度,通过求解机构速度雅克比矩阵可得出3种可影响灵巧度的指标:全局条件数指标、最小奇异值指标1/()、可操作度指标1/。将3个指标归一化处理后求和形成综合指标,用于评价机构全局灵巧度特性。
(1) 全域条件数指标。GOSSELIN等定义了全局指标全域条件数指标(Global Condition-number Index,GCI)评估机械手在工作区上的条件数分布,当=1时,机构处于运动学各向同性状态。表达式为

(12)
为局部条件数(Local Condition-number Index,LCI),在可达工作空间内的均值,反映机构条件数在全域范围内的各向同性。
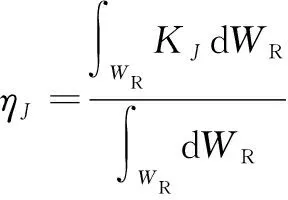
(13)
(2)最小奇异值指标。雅克比矩阵的最小奇异值()体现了输入与输出之间的最小传递放大倍数。()越大执行端对运动传递越快。令最小奇异值指标为1()。
(3) 可操作度指标。按YOSHIKAWA的定义,机器人雅克比矩阵与其转置矩阵乘积的行列式值的开方体现了机构距离奇异形位和不定形位的程度,为机器人的可操作度:

(14)
当=0,机构处于奇异形位;当=∞,机构处于不定形位;当≠0且≠∞时,机构处于非奇异形位。令1/为可操作度指标。
(4)综合灵巧度指标。先将、1()、1/进行归一化处理;再根据该机构的各向同性和响应速度,配置权重系数,设定=0.4、=0.4、=0.2,构造综合评价指标:
=[+()+]→min
(15)
3.2.2 动力学目标
对Delta机构的动力学逆解进行数值分析,假设动平台运动轨迹为典型门字轨迹,对机构刚度和灵巧度进行分析。
(1)刚度指标。当外力作用在末端执行器上时,机构发生形变,形变量关系着机器人动力学性能和位置精度,尤其对于并联机床或某些需要高精度的并联机械手,静态刚度(或刚度)是设计时的首要考虑因素。
在文中,仅考虑驱动机构的刚度(其他部分看作是刚体),通过应用动态和静态方程,得到局部刚度指标(Local Stiffness Index,LSI):

(16)

(17)
其中:为并联机器人的刚度矩阵。为全局刚度指标(Global Stiffness Index,GSI);由LSI在可达工作空间内的均值表示。优化时应满足:→min。

质量矩阵为
=()
(18)
设定局部动力学灵巧度指标(质量矩阵条件数)在可达工作空间内的均值,为全局动力学灵巧度指标,→min。、表达式为

(19)

(20)
(3) 综合动力学指标。根据DOE的结果,、趋势相近,则令动力学目标函数为
=(+)→min
(21)
(4)控制性能指标。在执行门字形轨迹运动时,机器人驱动力矩和功率的最大值越小越好。令性能控制目标函数为
=(+)→min
(22)
3.3 约束条件
3.3.1 结构尺寸约束
Delta并联机构的可达工作空间受到静平台和动平台铰接点分布圆半径差、主动臂、从动杆直径以及关节转角范围的约束。本文作者采用极坐标搜索法对进行取点,由图3可知,为顶部带有尖角的不规则几何体。
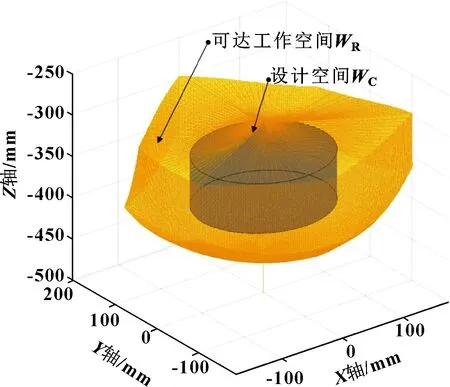
图3 Delta机器人可达工作空间
对旋转副转角进行约束:
min ≤≤max =1,2,3
(23)
对球副转角进行约束:
min≤≤max=1,2,3
(24)
连杆的干涉约束:
≥
(25)
其中:为任意相邻两杆间最短距离。
在实际应用中,所要求的设计工作空间一般是规则的(如长方体、圆柱体等),文中以圆柱体为设计空间,要求设计空间包含于可达工作空间,即∈。
3.3.2 运动学约束
在可达工作空间内,给定≤5且≥0.2的约束条件,以保证机构的各向同性,提高末端动平台的响应速度,同时避免奇异位形。
3.3.3 动力学约束

3.4 优化模型
该机构的优化数学模型可表述为
设计变量:,,,,
目标函数:

约束条件1:

约束条件2:

4 非支配排序遗传算法(NSGA-Ⅱ)
4.1 多目标优化问题
NSGA-II算法多用于解决多目标问题,NSGA-II在NSGA的基础上,增加了精英保留策略、计算拥挤距离值作为密度估计策略和快速非支配排序策略。该算法比NSGA效率更高,且不必选取参数。
4.2 算法流程
NSGA-II算法流程如图4所示。

图4 NSGA-II算法流程
5 优化结果
5.1 具体应用过程
NSGA-Ⅱ算法流程中参数设定:种群大小为24,运行代数为200代,交叉概率0.9,变异概率0.1。

步骤4中机器人各构件均质且为刚性,运动过程中不考虑摩擦因素影响,采用5次多项式构造门运动轨迹函数如图5所示。图中,起点(-100,0,-380)、中间点(-100,0,-330)、中间点(100,0,-330)、终点(100,0,-380)。
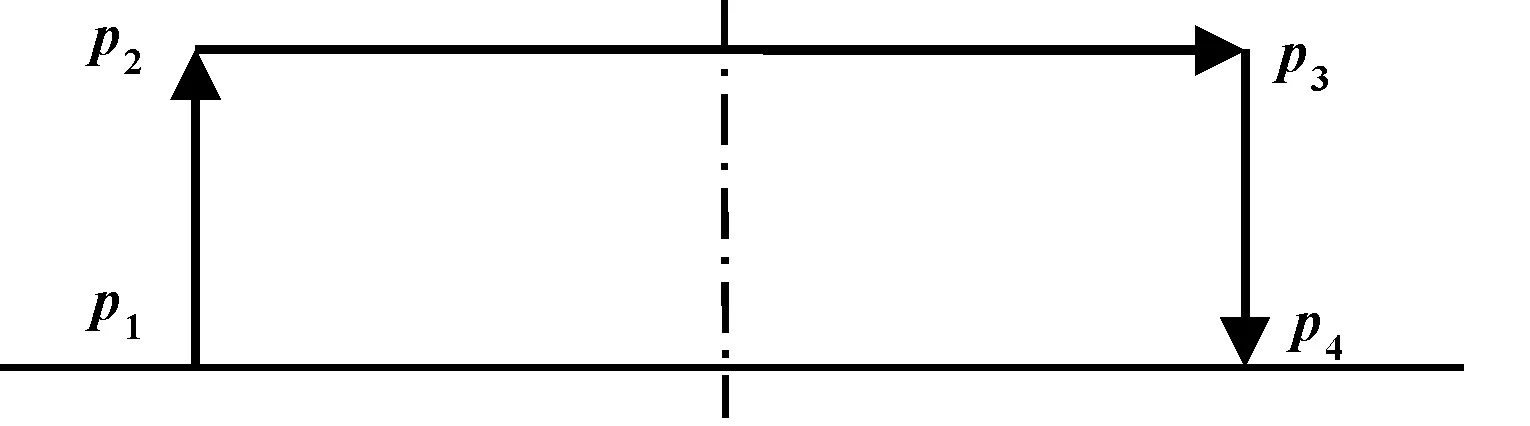
图5 末端动平台的运动轨迹
5.2 运算结果
通过iSIGHT软件迭代计算后得到Pareto前沿解,如图6所示。如表2所示,选取其中各项目标值较优的8组解,其中第0组为初始值作为参考;第1组为软件给出的最优解。
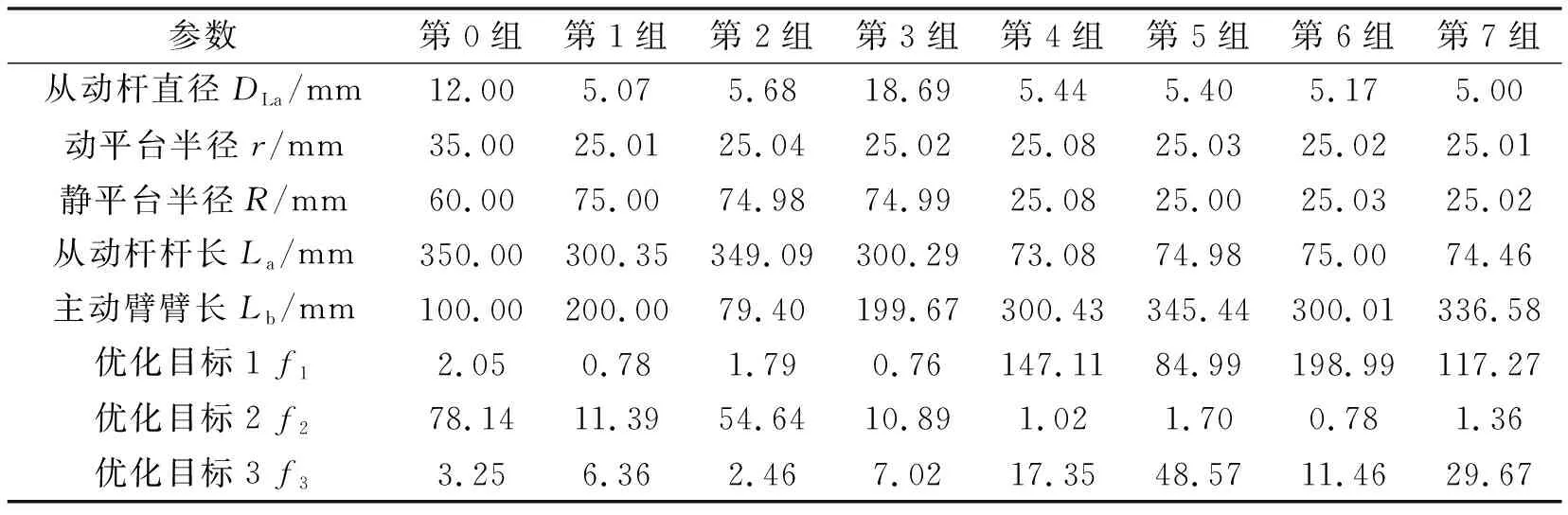
表2 多目标优化结果

图6 Pareto 最优解
为验证优化策略的可行性,设计不同维度的目标函数,对比的优化解集,对比方案中仅将拆分为2个单独目标=、=。结果表明:在使用同种算法、相同迭代次数下,方案1(3个目标函数)生成可行解624个、最优解13个,方案2(4个目标函数)生成可行解62个、最优解1个。
6 结论
本文作者通过DOE选定设计变量并建立目标函数,利用控制关键变量控制整体优化过程;通过整合趋势相近的目标,将目标数降为3个,相对于更高维度的目标数,文中的优化策略收敛性好,可视化程度强,计算费用大大降低,验证了优化策略的合理性。Pareto前沿图表明NSGA-Ⅱ算法在此次设计优化过程中,在保证机构满足设计空间和特定轨迹的条件下,能保持良好的综合性能,减小了整体尺寸,体现了优化策略的有效性。给出了部分Pareto前沿解供设计人员参考,后续还可加入模态分析、误差分析等使优化策略更加完善。

