关联维在砂体储层预测上的应用

李小霞，文晓涛，杨小江

（1.成都理工大学地球物理学院，四川成都 610059；2.中海石油有限公司深圳分公司研究院，广东深圳 518067）

分形几何（Fractal geometry）是20世纪70年代由法国数学家B.B.Mandelbrot创立的，它揭示了自然界中所形成的无规则的内在规律，已广泛应用于其它学科[1]。目前，在地震资料处理中，从地震道中提取属性参数来进行岩性与储层含油气特征研究，是地震资料处理的一种主要的技术方法。但是在我们从地震道中进行属性参数提取时，大部分都是基于线性分析理论。而实际上，地震道是一个典型的非线性时间序列，在标度范围内普遍具有标度不变性和自相似性[2]。因此，基于动力学非线性理论，利用非线性时间序列分析的方法和技术来进行地震道属性参数提取才会对地震信息的合理利用更有利。

在石油勘探中用于计算地震记录时使用的主要是关联维，它反映了以一定的嵌入维数为尺度对地震序列进行剖分，若剖分后各段地震序列之间的相似性好，则关联维就增大，否则相反。含油气层与不含油气层地震序列经剖分后各小段地震序列之间相似性有差异，即关联维的大小反映了处理时窗内地层变化复杂程度。由于地质构造和岩性的复杂多变，使得地震反射信号极不规则[3-5]。因此，关联维数的大小反映了地震反射系列的复杂程度。本文主要研究和提取的地震属性参数就是动力学非线性系统中不变量—关联维。

1 地震属性关联维求取原理

由于地质构造和岩性的复杂多变，导致地震反射信号极不规则。因此认为地震道是一个混沌时间系列，具有介于一维和二维之间的分维数，这个分维数可以用重构相空间的方法来确定。重构一个相空间的目的使这个时间系列在一个合适的空间坐标中能够显示出混沌吸引子的结构。计算出的分维值就是地震道的关联维，常用D表示，它对油气层的反映较为直接而敏感。D值取决于地震道的波动形态，储集层中是油、是气、还是水，有不同的波阻抗，产生不同的反射系数，就会有不同的波形，因此就会有不同的D值[4-6]。

1.1 相空间重构

将地震道针对目的层开时窗，设地震道的采样点数为n，某道的采样点可以表示为：

采用延迟坐标法将其重构组成一个m维的向量空间xN｛｝，即：

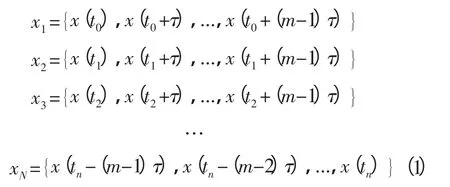
这是按采样间隔τ顺序构成的向量。这实际上相当于移动时窗，时窗宽度为m个样，即为（m-1）τ。N=n-（m-1）τ为重构向量数。

1.2 计算相关函数

建立相空间后，求取任一点对xi，xj之间的欧氏距离Lij：

任意设定一个标度r，并统计距离小于r的一切点对的数目在全体点对数（N2）中的比例，其中N为相点数。

考虑到度量空间距离的对称性，（3）式可进一步写成：

上式为关联积分，式中 （x）为Heaviside函数，即：

1.3 求关联维数

r选择合适的空间时，C（r）随r呈幂级数形式变化，即：

取对数有

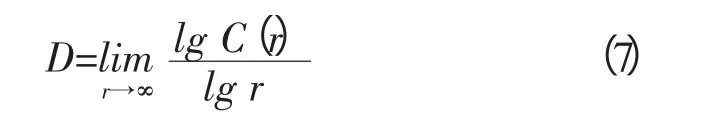
2 无标度区间的确定

在实际计算中，首先，标度r的取值要适中。为保证r的取值在无标度区间内，r值存在满足条件：

其次，由于信号采集的数据长度也会影响到参加数据拟合的点数，从而影响到无标度区间的确定。因此综合上述两个方面，计算方法如下：计算出重构相空间中两点距离的最大值和两点距离的最小值设标度的单位长度为Δt（Δt的取值应根据不同的分析对象分别考虑），取步长k=ss，标度r的方程为：

经过取不同的ri（i=j，j+1，...，n，j≥1）能够得到一系列的Cm（ri）；将得到的ri和Cm（ri）取对数用最小二乘法进行拟合，得到图像的斜率值即为该系统的关联维数。

3 理论模型数值分析

针对研究砂体储集层的关联维情况，建立了两套理论地质模型。砂体地质模型1（见图1（a）），围岩速度为4 000 m/s，储层砂体速度为3 500 m/s；模型2（见图1（b）），盖层泥岩速度为 3 300 m/s，下部砂层速度为3 000m/s，中间储集层速度为2 800 m/s。采用频率波数域波动方程数值模拟方法对地震波场进行正演模拟（见图1（c）、图1（d）），不仅求解速度快且很好地保留地震波场的运动学和动力学特征[8，9]。

图1（e）和图1（f）为对理论模型计算出的道内关联维剖面。图1（e）表明，在砂体边界关联维值明显降低，薄层砂体的顶底位置明显。而在图1（f）则可看出，关联维可识别薄层砂体及泥砂层分界面，但不能分辨出厚层砂体的存在。图1（g）和图1（h）为沿层道间关联维曲线，在储集层位置关联维值降低。

4 应用实例及效果

通过关联维计算结果对已钻井区进行检验。通常选择过已知井的过井剖面，根据砂层和油层的厚度确定适当的时窗（为确保其精度，所取的时窗一般不超过15 ms），来验证上述计算结果是否能有效地反映储层和油气的变化，并通过调整时窗等参数，在保证与钻井完全吻合的前提下，再进行未知区的预测。

本文研究区域为塔河YY区，该区三叠系构造较平缓，主要受N-E向断裂带和盐体的塑性活动控制，沿N-E方向延伸形成大型圈闭群。三叠系发育的储层主要有上、中、下三油组的砂体。本文针对中油组砂体进行研究。图2（a）为过THN1井剖面，单从原剖面上很难分辨砂体的发育程度及砂体的边界；图2（b）为沿地震道方向计算的关联维过井剖面，则可以清楚识别砂体储集层位置，且在砂体储集层上其D值明显降低。图2（e）是对计算的道内关联维数据体提取的沿层切片，图2（d）为沿层（道间）方向计算的关联维切片。比较图2（e）和图2（d）可知，沿层方向所得关联维对砂体范围显示更清楚，并且在围岩及储集层砂体上的关联维值基本稳定。

5 结论与建议

结合模型与实例分析证明，关联维在砂体储集层检测上具有一定的效果。

（1）道内关联维反映的是某时窗地震记录的综合信息，结合地质和钻井进行综合分析的基础上，可以判别砂体的发育程度、确定砂体储集层位置。但由于波形本身具有复杂性，造成砂体预测的多解性。

（2）道间关联维反映的是道间岩性展布，因其受波形变化影响少，所以在围岩及储集层砂体上的关联维值基本稳定，可清楚显示砂体范围。

（3）关联维应用于储层预测，其变化既可能是由于地层、储层变化引起，也可能是含油气造成的，因此在不同地区，应根据不同的地质模型，合理地进行储集层预测和油气检测。

［1］H.S.Kim，R.Eykholt，J.D.Salas.Nonlineardynamics，delay times，and embedding windows［J］.Physica D，1999，（127）：48-60.

［2］隋少强，宋丽红，李淑敏，等.分形理论在储集层横向预测和油气层判断中的应用［J］.新疆石油地质，2001，22（4）:342-344.

［3］文晓涛，贺振华，黄德济.基于小波包变换与关联维的储集层检测［J］.新疆石油地质，2007，28（5）：569-571.

［4］文晓涛，贺振华，黄德济.基于小波包变换与关联维的储层检测［G］.中国地球物理学会第22届年会论文集，2006.

［5］党建武，等.基于分形理论的地震信号空间序列分析［J］.西安石油学院学报（自然科学版），2003，18（4）：11-14.

［6］姜素华，等.地震道的分形维计算及在滩海地区油藏描述中的应用［J］.中国海洋大学学报，2006，36（5）：841-844.

［7］贾子文，等.分形理论中无标度区间的识别方法［J］.设计与研究机械，2012，11（39）：24-30.

［8］周怀来，等.各向异性介质储层数值模拟及波场特征研究［J］.物探化探计算技术，2010，32（4）：345-353.

［9］陈可洋，杨微，吴清岭，等.几种地震波叠后深度偏移方法的比较［J］.勘探地球物理进展，2009，32（4）：257-260.