GRAPES-GFS模式2 m温度预报的最优时窗滑动订正方法
何珊珊 蓝盈 戚云枫
(广西壮族自治区气象台,南宁 530022)
引言
近年来,数值天气预报发展迅速,并凭借其客观化、定量化的优势在天气分析、精细化要素预 报等方面发挥了不可替代的作用。全球区域一体化同化预报系统GRAPES(Global/Regional Assimilation and Prediction System)自投入业务运行后,已经成为全国天气预报业务的主要参考之一。目前广西区内对于数值预报的检验评估、订正方法研究和成果应用等大多是基于ECWMF模式,针对GRAPES-GFS模式产品的分析应用仍停留在主观分析方面,对其系统性的检验评估和客观订正方法研究仍为空白。不论从支撑广西智能网格气象预报业务的需求出发,还是从为改进GRAPES-GFS模式提供客观依据的角度来看,加强GRAPES-GFS模式产品本地应用,开展系统性定量化检验评估、研发和优化产品释用方案的工作都是非常必要的。
为了减少数值模式误差、改进数值预报,气象工作者们提出了许多动力-统计相结合的释用方法,例如统计-动力预报、模式输出统计(Model Output Statistics,MOS)、线性回归方法、非线性回归方法和卡尔曼滤波等方法[1-6]。目前,在广西气温预报本地释用技术的现有研究中,多采用如MOS、神经网络、逐步回归、卡尔曼滤波、模式距平积分订正等方法[7-9]。滑动平均订正法以简单平均数法为基础,通过对前期某一段时间(训练期)的预报误差取算术平均,将其作为订正量订正当前预报,达到消除模式系统误差的目的。与其他订正方法相比,滑动平均法计算量小,对历史资料需求量小,具有更好的可操作性。但问题在于,滑动平均方法的订正效果对时窗长度的选取有依赖性,必须选取合适时窗长度才能获得合理的订正方案。时窗长度过短,不能有效地消除随机误差;时窗长度过长,则可能会因为模式动力框架、参数化方案等原因导致的系统误差存在季节变化,使得订正量的可用性降低。另一方面,数值天气预报在短时效和长时效的系统误差不同,相同的时窗长度不能适用于所有预报时效。当前,广西预报业务中应用滑动订正法时,通常采取固定时窗的方式,即对所有预报时效都采用相同的时窗长度,并且时窗长度的选取大多没有经过严格检验,带有一定的主观性。国内众多学者分析了滑动订正法的效果,但采用的时窗长度不一。如王强等[10]利用1~5 d滑动平均法订正了ECMWF对湖南怀化的最高气温预报,发现不同时窗滑动平均订正的差异小,且方法操作简便、简单实用。王婧等[11]利用多种方法对GRAPES_RAFS模式2 m温度偏差进行订正,指出采用15 d滑动时窗的滑动平均法可以有效减小模式预报误差。盛春岩等[12]对几种气温客观预报方法进行研究,指出通过10~30 d 的偏差滑动订正可以提高ECMWF模式的预报准确率。
为了解决上述问题,本文拟对GRAPES-GFS模式广西区域地面2 m温度预报进行偏差分析,确定模式预报是否存在系统偏差,并进一步通过活动时窗长度的方法,设计不同的滑动平均订正方案,制定最优时窗滑动订正方案,以期获得本地适用的GRAPES-GFS模式地面2 m温度预报产品客观订正方法。
1 资料和方法
1.1 资料
本文使用的资料为2017—2018年GRAPES全球模式(GRAPES-GFS)的地面2 m温度3~240 h时效预报(简称GRAPES-GFS温度预报)和广西区域自动站逐时气温观测资料,其中,3~120 h时效内为逐3 h间隔、120~168 h时效为逐6 h间隔、168~240 h时效为逐12 h间隔;广西区域自动站逐时气温观测资料来源于全国综合气象信息共享平台(CIMISS),所采用的广西区域气温观测站数据已经过质量控制(质控码为0、3、4),站点总数为1700多个;分析区域选取为104.5°~112.0°E,21.125°~26.375°N,网格水平空间分辨率为0.25°×0.25°,站点分布见图1。利用临近法,站点实况插值到0.25°×0.25°网格点形成网格实况场,网格点取值为与其距离最近的站点有效数据。在季节的划分上,本文分析的春季为3—5月、夏季为6—8月、秋季为9—11月、冬季为12月至次年2月。在样本独立原则下,本文以2017年模式预报为基础,对比分析订正后2018年四季的订正效果。本文制定的最优时窗滑动订正方案于2021年1月开始投入广西智能网格气象预报业务应用,前期积累了1年多的试验运行数据。为验证该方案的应用效果,在本文最优时窗订正方案订正效果分析部分,对比了该方案在2018年和2020年的订正效果。

图1 广西区域气温自动观测站分布
以往研究发现日最高温度和最低温度的预报误差有显著的差别,而08:00起报(北京时,下同)和20:00起报的最高温和最低温出现的预报时效通常是不同的。为了避免温度日变化可能对检验结果造成的影响,将GRAPES-GFS温度预报分为08:00起报和20:00起报2组分别检验。由于GRAPES-GFS温度预报20:00起报场的偏差特征和订正方法研究与08:00起报场基本一致,本文以模式20:00起报场的偏差分析和订正为例进行细致讨论。
1.2 检验指标及最优判别依据
1.2.1 检验指标
本文所用的误差检验指标有平均误差ME(ME),平均绝对误差MAE(MAE)、均方根误差RMSE(RMSE)以及预报偏差2 ℃以内的准确率ACC(ACC):
其中,F表示预报值,O表示观测值,i、j表示该值为第i个网格点在第j个时间的值,m为网格点总数,n为预报次数,Nr为报对次数、Nf为预报总次数。
ME反映了统计时段和检验区域内预报偏差大小的整体情况,ME正偏差表示预报比实况偏大、负偏差表示预报比实况偏小。MAE反映了统计时段和检验区域内预报值与实况的平均偏离程度,MAE越小表示预报越准确。RMSE反映了误差的离散程度,RMSE越小表示误差的在时间和空间上的变化越小、预报越稳定。ACC反映了预报误差偏差2 ℃以内的比例,ACC越大、预报正确率越高。就单个网格点而言,在统计时间段内,MAE、RMSE有较好的一致性,MAE越大、RMSE越大,表示偏差幅度越大、预报稳定性越差。
为评估订正效果,本文定义一个订正技巧指标,即对于某个检验指标,其订正技巧指标等于订正前的检验指标减去订正后的指标。例如,MAE的订正技巧IMAE=订正前的MAE-订正后的MAE。若技巧IMAE为正,订正后的MAE小于订正前,即订正后MAE减小,有订正效果;若技巧IMAE为负,订正后的MAE大于订正前,订正后MAE增大,无订正效果。同理,IRMSE为正时,订正后RMSE减小,有订正效果;IACC为负时,订正后ACC增大,有订正效果,IACC越小(绝对值越大),订正效果越好。
1.2.2 最优时窗判别依据
对于最优时窗,本文制定最优判别依据如下:在评估期(训练期)内,IMAE非负的所有时窗中,以IMAE最大者为最优滑动时窗;若时窗不唯一,则再考察IMAE最大时窗的IRMSE,以IRMSE最大的时窗为最优;若时窗仍不唯一,进一步考察IMAE最大且IRMSE最大时窗的IACC,以IACC最小的时窗为最优。
2 模式2 m温度预报偏差特征
为考察GRAPES-GFS模式2 m温度预报性能,分季节计算20:00起报的各时效预报检验参数。由区域平均MAE和ME随时效的变化(图2)可见,对于GRAPES-GFS模式 20:00温度预报(简称GFS20),广西区域的MAE在2 ℃左右,随时效增加而波动式增大。整体而言,MAE及其随时效而增大的幅度冬季最大、夏季最小,春秋季节介于两者之间。在短中期时效(3~168 h,下同)内,MAE具有明显的日变化特征:日间MAE明显大于夜间,最大出现在18 h、42 h、66 h、90 h、114 h、138 h、162 h时效,即14:00,峰值在2.5~3.5 ℃左右。夜间,MAE的谷值出现在3~9 h、27~33 h、51~57 h、75~81 h、99~105 h、126 h、150 h时效,对应于23:00至次日05:00。从峰谷值的季节差异上看,MAE的峰值春季最大、夏季最小,两者相差0.5 ℃左右;MAE的谷值冬季最大、夏季最小,两者相差1 ℃左右。

图2 2017—2018年GFS20的不同季节广西区域平均的平均绝对误差(折线,点虚线为逐12 h预报)及平均误差(柱状)(GFS20为GRAPES-GFS模式20:00温度预报,下同)
相比而言,在全时效内,广西全区平均ME均为负偏差,在-1~0 ℃附近摆动,即温度预报整体偏低,随时效增加变化不大。在短中期时效内,ME也有具有明显的日变化特征,ME的最小值和最大值分别出现在午后和午夜到凌晨,分别在-2.5 ℃和-0.5 ℃左右,即预报偏低的幅度午后大于夜间。
另外,根据MAE和ME的相对大小,可以定性分析四季预报偏差中随机误差和系统误差的相对大小。结合MAE的日变化特征可以发现,对午后气温,模式预报四季MAE在0.5 ℃以内、季节差异不大,但冬季ME的偏差幅度明显小于其他季节,可见午后气温预报偏差在冬季随机性较大,在春夏秋季节则具有明显的系统性。对凌晨气温,除了3~24 h时效内MAE和ME对应关系较好,预报偏差还具有一定的系统性以外,多数时效ME并没有明显的季节差异,但四季MAE之间差异十分明显,预报偏差存在较大的随机性。
分析全区平均的MAE、RMSE和ACC(图略)发现,MAE和RMSE随时效的增加而逐渐增大,ACC随时效增加而减小,且季节差异及日变化特征具有很好的一致性:RMSE冬季最大、夏季最小,ACC冬季最小、夏季最大,MAE达到峰值(谷值)时,RMSE也达到峰值(谷值),ACC为谷值(峰值),表明当预报偏差大(小)时,预报偏差在时间和空间上的差异较大(小)。
为进一步了解预报偏差的空间分布特征,下面以最接近起报时的05:00(MAE谷值、ME最大值)和14:00(MAE峰值、ME最小值)气温预报为例进行细致分析。图3a~d为GFS20预报凌晨气温(05:00)的ME和MAE空间分布,黑点区为超过全区平均的MAE相对大值区。可见,除了沿海地区四季都出现了超过3 ℃的ME正偏差区、模式预报气温偏高外,广西大部地区ME以负偏差为主,在-3~-1 ℃以内。MAE和ME的大值区多出现在桂北山区、左右江河谷及沿海,上述地区预报偏差以系统偏差为主。对于午后气温(14:00,图3e~h),广西大部ME四季均为负偏差、预报以偏低为主,ME的正偏差区只出现在来宾金秀(大瑶山)、玉林容县(大容山)及防城港上思(十万大山)等地。MAE和ME的大值区(系统性偏差区)集中出现在桂北山区以及左右江河谷,其中在桂林、贺州、柳州北部、河池及百色等地ME可低至-3 ℃以下。

图3 GFS20 9 h预报(次日05:00)(a~d)和18 h预报(次日14:00)(e~h)的四季平均误差分布(黑点代表超过全区平均值的平均绝对误差,单位:℃)
GFS20其他时效预报的午后和凌晨气温偏差的大值区分布与9 h和18 h基本一致,时效越长、偏差幅度越大。GFS08对起报日的次日05:00和当日14:00温度预报的偏差分布(图略)与GFS20相似,ME偏低的幅度及MAE超过全区平均值的范围较小,四季之间差异的情况与GFS20一致。
3 滑动订正方案订正效果分析
本文以1 d、2 d、3 d、4 d、5 d、10 d、15 d、30 d、60 d为基础,根据训练期或时窗选择方式的不同,制定2种滑动订正方案:
(1)方案A:固定时窗订正。即分别以各基础时窗对所有时效进行滑动平均订正,没有训练期,各订正方式分别简称为1 d、2 d、3 d、4 d、5 d、10 d、15 d、30 d、60 d订正。以此方案订正3~240 h时效(3 h至10 d)预报产品,需要存储的历史资料长度最少10 d、最多70 d。
(2)方案B:季节最优时窗订正、月份最优时窗订正(分别简称为SN订正、MO订正)。训练期为2017-01-01至2017-12-31(1年)。即订正前需判定训练期内各季节(月份)的最优时窗,订正时则根据起报时所处的季节(月份),选择对应的最优时窗进行订正。本方案设计主要基于模式预报系统性误差的季节特征或月际特征,与方案A相比,需要累积存储订正开始前至少1年的历史预报和实况资料。
图4为订正前后2018年四季的预报准确率ACC、图5为订正后2018年四季的各时窗平均绝对误差订正技巧IMAE。由图可见,滑动时窗越长、订正效果越好,订正效果在15 d以后趋于稳定,且春夏秋3季午后的订正效果都好于夜间。冬季,GFS20预报ACC在50%左右,在3~24 h时效所有滑动订正方式均有订正效果,其余时效只有30 d订正、 60 d订正、SN订正和MO订正这4种方法具有订正效果,但订正效果十分有限,IMAE在0~0.5 ℃附近摆动,ACC提高5%~10%。夏季,各滑动订正方式中,除短时窗1 d订正外均有订正效果。其中,方案A长时窗(≥15 d)订正(15 d、30 d和60 d订正)和方案B的订正效果最佳,IMAE在0.5~1 ℃左右,随时效增加没有明显变化,IACC约为-20%~-10%,滑动订正能使夏季午后ACC提高到60%左右,夜间ACC提高到90%以上,这几种订正方式的效果比较接近。

图4 订正前(Origin)与订正后的2018年冬季(a)、春季(b)、夏季(c)、秋季(d)的预报准确率ACC(1 d、2 d、…、60 d为固定时窗订正;SN为季节最优时窗订正;MO为月份最优时窗订正,下同)

图5 订正后的2018年冬季(a)、春季(b)、夏季(c)、秋季(d)的平均绝对误差订正技巧IMAE
春秋季节,滑动订正效果介于夏季与冬季之间。除了秋季12~24 h时效的方案A短时窗订正方案(1~5 d订正)和MO订正的效果较好外,春秋季多数时效的15~60 d订正、SN订正和MO订正的效果最优。其中,15~60 d订正的订正效果在春季稍好于SN订正和MO订正,但在秋季这几种订正方式的订正效果相当。
由上述分析可见,利用滑动订正方案A和方案B,均可以不同程度地降低预报偏差。结合前述的预报偏差分析结果可知,在预报误差以系统性为主的春夏秋三季,订正效果最佳,滑动订正效果在短中期时效有明显的日变化特征、午后订正技巧高于夜间。在多数时效中,滑动时窗越长、订正效果越好,15~60 d订正、SN订正和MO订正的订正效果好于其它方案,SN订正与MO订正的订正效果差异不大。
4 最优滑动方案订正效果分析
从上述分析可见,长时窗(15~60 d)订正、SN订正和MO订正对GFS20多数时效预报有较好的订正效果,但滑动时窗的最优除了与滑动时窗的选择有关,还和训练期、评估期的长短有密切关系,利用方案A和B中的任一订正方式并不能稳定地在所有时效、所有时段中获得最优的订正效果。因此,为使滑动订正效果稳定,本文制定的最优时窗滑动订正方案,是在滑动时窗订正方案A和B的基础上,通过一段时间的训练(评估),在训练期内选定最优时窗再用于实际订正。在实际订正中,训练期为每个起报时的前N天,订正时所用的滑动时窗,为训练期N天内评估挑选的最优时窗。例如,若设置训练期为5 d,订正前需对起报时前5 d内的所有滑动订正结果进行评估,选择订正效果最优的时窗作为当前起报时的最优订正时窗。由于训练期的时间长度固定、时间不固定,此方案的最优时窗是动态的。训练期长度N的确定,成为最优时窗滑动订正方案的关键环节。与订正方案A和B相比,本方案需要存储训练期内所有滑动方案的订正场,耗费一定存储空间。
为了排除训练期长短对订正效果的影响,寻找适用于GRAPES-GFS模式广西本地2 m温度预报的训练期,本文分别将N设置为1、5、10、15、30、60、90进行考察(各训练期订正分别简称为Dyn1、Dyn5、…、Dyn60、Dyn90订正),通过评估各训练期的订正效果确定合适的训练期N。
从订正后的IMAE(图6)来看,最优滑动方案订正效果明显,随训练期延长,IMAE增大,订正效果在30 d训练期后基本稳定。除了短训练期(≤15 d)在冬季IMAE为负、没有订正效果以外,Dyn30、Dyn60、Dyn90订正在四季均有订正效果。从60 d订正、SN订正、MO订正和Dyn30订正在2018年全年的订正效果(图7a)来看,这4种订正方式的订正效果十分接近,IMAE相差不到0.1 ℃,ACC相差不到2%(表略),60 d订正在各时效中的表现最佳。但在业务运行的试验阶段(2020年,图7b),60 d订正的效果最差,多数时效的IMAE为负、没有订正效果,SN订正与MO订正的效果几乎一致,Dyn30订正的效果最好。由此可见,实际订正中采用30 d训练期的最优滑动订正方案(Dyn30订正),可以在不同滑动方案的基础上稳定地提高预报准确率,达到最优时窗滑动的目的。

图6 经过最优时窗滑动订正方案不同训练期订正的2018年冬季(a)、春季(b)、夏季(c)、秋季(d)平均绝对误差订正技巧IMAE(Dyn1、Dyn5、…、Dyn90分别表示滑动时窗的训练期分别为1 d、5 d、…、90 d,下同)
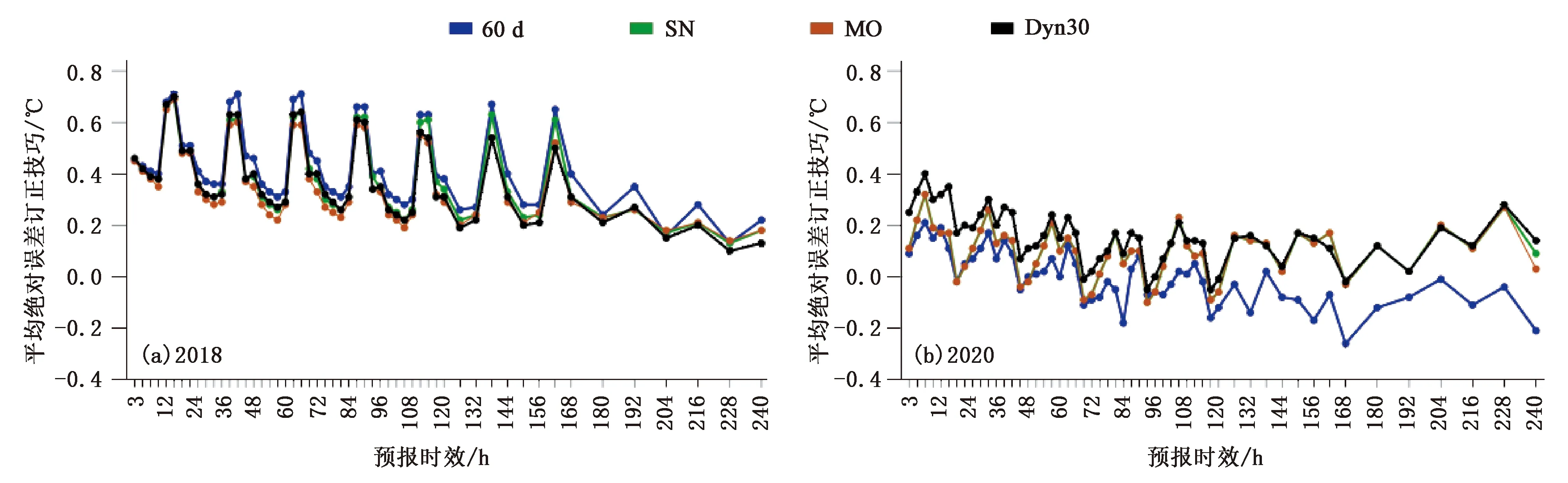
图7 经过固定60 d订正、SN订正、MO订正和Dyn30订正的2018年(a)、2020年(b)平均绝对误差订正技巧IMAE
5 结论
本文通过GRAPES-GFS模式对广西2 m温度的预报偏差特征分析,确定了模式预报存在系统偏差的事实,并进一步通过活动时窗长度的方法,设计不同的方案,制定最优时窗滑动订正方案,得到如下结论:
(1)GRAPES-GFS模式对广西区域2 m温度的预报系统性偏低,随着时效增加,预报偏差增大。日间气温的预报偏差明显大于夜间,午后气温的预报偏差在春夏秋3季以系统偏差为主、在冬季以随机偏差为主,四季凌晨气温的预报偏差在多数时效有较大随机性;在空间分布上,系统性偏差主要出现在桂北山区、左右江河谷及沿海。
(2)采用滑动平均的固定时窗订正、季节最优订正和月份最优订正方案,可以不同程度地减少GRAPES-GFS模式的预报误差、提高预报准确率。在预报误差以系统性为主的春夏秋3季,滑动订正效果明显好于冬季,午后订正技巧高于夜间。与其他滑动方式相比,15~60 d订正、季节最优时窗订正和月份最优时窗订正的效果最优。
(3)所制定的最优时窗滑动平均订正方案建立在对训练期内不同滑动订正方式订正效果评估的基础上,它可以在不同滑动方案的基础上稳定地提高预报准确率,达到最优时窗滑动的目的。

