一种基于改进时窗法的爆炸冲击波检测方法

艾斯煜，杜博军，王 军,3

(1.苏州科技大学, 江苏 苏州 215009; 2.中国人民解放军63850部队， 吉林 白城 137001；3.中国科学院 长春光学精密机械与物理研究所, 长春 130033)

一般在靶场测试系统中，爆炸冲击波的检测对象主要是空气超压。而气压检测系统易受爆炸所产生的光辐射和热辐射影响。就本文中仅涉及的地面爆炸冲击波检测系统[1-2]而言，可以通过地下浅埋加速度传感器检测冲击波的加速度值实现。

在爆炸冲击波检测领域，研究重点多为传感器数据采样，尤其是结合了前端数据处理的高精度采样问题。冲击波中有效信号拾取是研究的关键，其方法主要有滑动窗口法和相关耦合法。滑动窗口法是指在每个滑动产生的窗口中计算窗内时域波形的特征函数，根据函数的变化特征情况来标示冲击波的存在，并通过分析起突变情况以拾取冲击波初至。而相关耦合法主要基于相邻信道之间的波形相似性，对冲击波波形信号上的部分或者整体波形截取并将其时间延迟，最终与待测冲击波信道上的记录对比以获得冲击波信号的存在性并确定波峰到达时间。

滑动窗口法的最新应用有学者时伟等[3]提出的双约束变换时窗能量比法，该方法计算步骤简单，初至拾取效率高；左国平等[4]提出的滚动能量比法，提高了计算精度和准确度；郑江龙等[5]提出的能量差法，将计算能量和比值转换为能量差比值，提高了时窗检测灵敏度。该类方法虽然对多路信号独立处理，无需考虑信号关联性问题，运算简单、数据处理效率高，但对高频低信噪比信号获取效果较耦合法不明显。

相关耦合法的最新研究成果有北京大学喻志超等[6]提出的利用波形相似性进行初至时刻拾取的时窗选择法,解决了冲击波的微变化数据提取问题；魏梦祎等[7]学者提出了一种结合STA/LTA方法的基于波形互相关的冲击波初至拾取方法，联合多路数据为一个整体处理,实现初至获取结果全局优化；Akram等[8]国外学者基于迭代的互相关算法并在初至时刻获取方面应用，有效识别了地震冲击波的微变化。但该类方法普遍存在对高频非线性、关联性较弱的信号拾取效果不明显等问题。

本文提出了一种结合了变窗长峰值滤波和耦合量互信息特性的改进时窗法。以建模仿真、实验测量相结合的方式，完成了对爆炸冲击波等实验数据的采集和效果偏差等后端数据处理。通过与传统时窗法[9]对比，验证了该爆炸冲击波检测方法的可行性。

1 方法原理

1.1 时窗能量对比法拾取冲击波信号

在三轴加速度传感器组成的冲击波检测系统中[10-11]，冲击波初至时刻是一个非常特殊的时刻，即此刻之前所记录只有噪声，而后所记录则是噪声与冲击波的迭加信号。由于初至前后两时窗积分能量有较大差异，故利用该特性来判断初至时刻的发生点。时窗能量比E(i)反映了峰值时窗与前一时窗的变化程度,其表达式为：

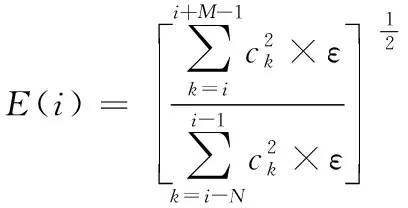
(1)

其中，ck表示加速度传感器测量值(m/s2)；M表示下一个时窗大小(s)；N表示当前时间窗大小(s)；ε表示测试环境中的背景噪声系数；i表示当前时刻相邻最大整数值。

传统时窗能量对比法受固定窗长制约，信号的高、低信噪比部分均采用同窗长采样，致使结果中高信噪比部分混叠较多噪声信号，故而感知能力不佳，拾取精度不高。

1.2 互信息量概念

将随机变量考虑成通信系统，两信道即为2个相关变量。互信息量I(x，y)表示两个相关变量之间的统计学依存度，取值范围为0～1。其中xi表示该系统的输入量，yi表示系统的输出量，通过互信息量这一概念建立两路采集信号相关性。

互信息量表达式为：

(2)

式中：p(xi，yj)为2个变量的联合分布；p(xi)、p(yj)为边缘概率分布；o和s分别是X和Y的发生数量。

1.3 改进后的时窗法拾取冲击波信号

由于传统时窗法中窗长固定且对信号的高频低信噪比部分感知效果差，进而导致采样精度低。本文结合变窗长峰值滤波和互信息量概念对传统时窗法进行了改进。

变窗长峰值滤波是一种信号增强方法，操作步骤如下：

步骤1：加速度传感器所直接采集输入时域信号x(t)通过频率调制得到解析信号z(t)：

(3)

在实际研究中原信号x(t)可表示为：

x(t)=s(t)+v1(t)

(4)

其中：s(t)是A通道加速度有效值；v1(t)是该通道的任意噪声。

步骤2：对z(t)进行Wigner-Ville转换，获得的时频域信号Wz(t，f)为：

(5)

其中：h(τ)为时窗调节函数，表示时窗长度且会随所测数据做出调整；τ为时间变量(s);f为自变量频率(Hz)。

步骤3：求取s(t)期望值，求取过程为:

(6)

其中：μ表示缩放比，由实际测试信号的强度设置。式(6)表示在对应频率f取值能让Wz(t，f)最大时，所对应时域函数按一定比例缩放。

步骤4：选取时窗。考虑到震动模型与Ricker小波信号模型(如图1所示)相似，时窗长WL的选取参照Ricker小波信号模型常用式(7)，α为时窗选择比，默认0.707。针对冲击波不同频段，fs为波峰对应频率(Hz)；fd为有效信号带宽(Hz)； 对应时段为Ts、Td，单位都为s。

(7)

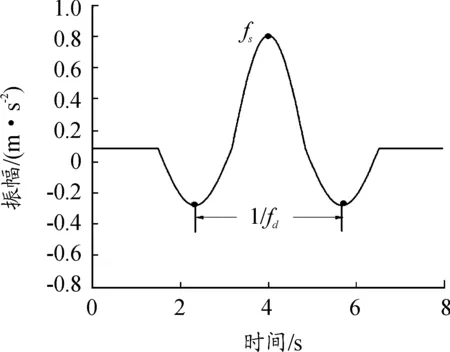
图1 Ricker小波信号模型

令2个地震信道记录A和B采样信号为x(t)和y(t)，根据冲击波一般观测方法和传播特性，信号满足以下模型：

x(t)=s(t)+v1(t)

y(t)=Q[s(t-D)]+v2(t)

(8)

B通道中Q[s(t-D)]是非线性时不变函数，它主要描述了传播过程中冲击波的波形变化程度。D是一个延迟参数，v2(t)为B通道观测噪声。通过检测y(t)中不同延迟点D处的冲击波形，并综合通道A观测信号x(t)进而对冲击波估计分析。

互信息量反映随机变量间的统计关联度，且不依赖于线性关系，可以有效避免非线性函数带来的不利影响。在测量模型中x(t)为冲击波信号，x(L)是波峰附近选择的一段时窗，由于传播通道间存在时延，可以将通道B看成A的输出关联量y(L+d)，即输出量为输入时窗长加一段函数延迟d。在时窗大小不断改变和移动的情况下，求取对应互信息量I(x，y)，I(x，y)最大值时关联性达到最强，即此窗口时刻为该通道的初至时刻。

获取A、B通道数据步骤如下：

1) 通过A、B通道加速度传感器测量得到冲击波数据x(t)，y(t+d)，计算得到其互信息量I(x，y)。

图2给出了改进算法的流程。

1.4 爆炸冲击波超压等效换算

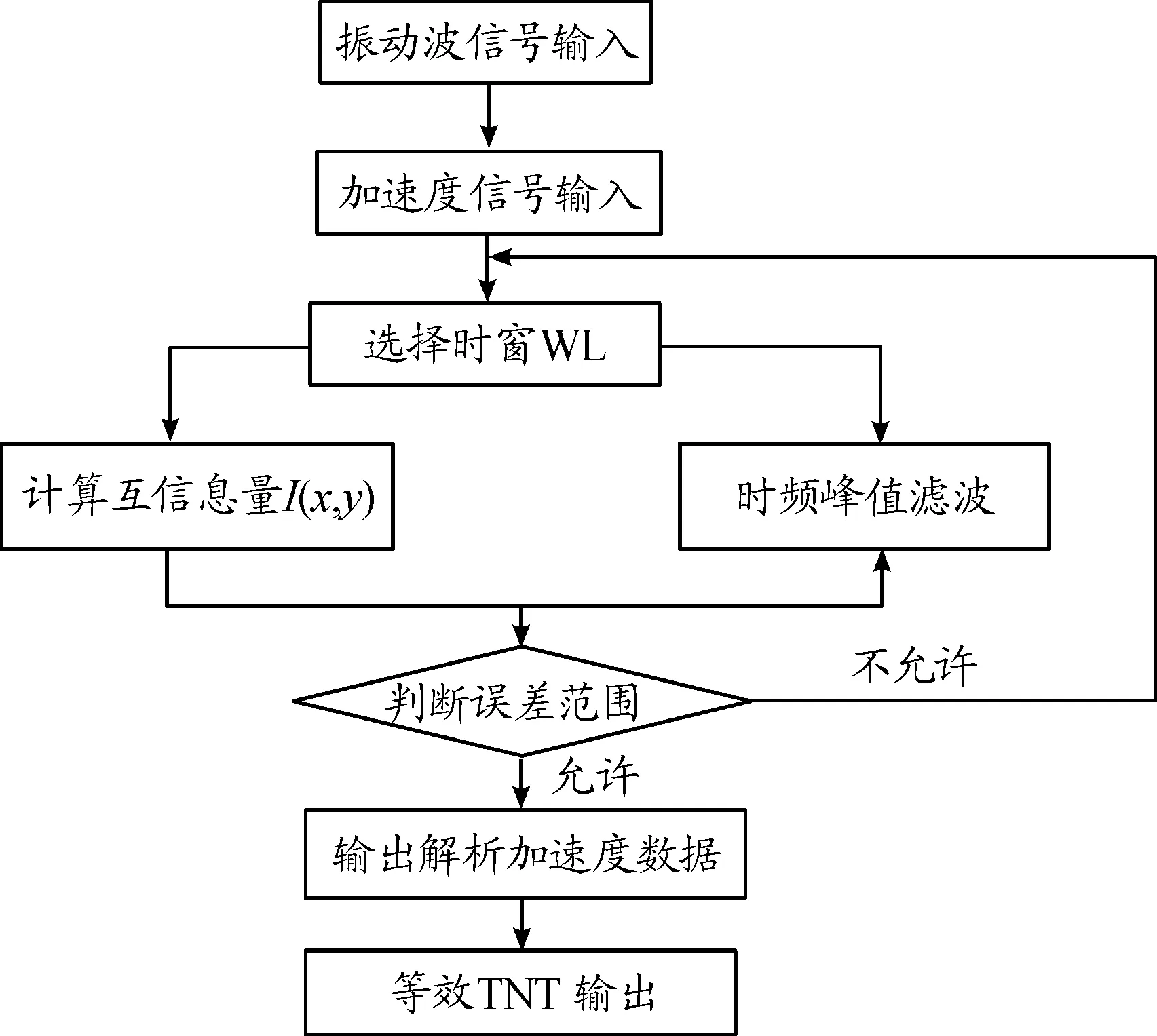
图2 改进算法流程框图

1.4.1加速度数据压强转换公式

通过实际测量和查阅相关资料[15-16]，压电式加速度传感器测量值与施加于其上压强可以通过工程公式进行转换，公式如下：

(9)

反向推导得：

(10)

式中：R为检测装置与炸点中心间距(m)；d为传感器探头部分厚度(m)；amax为加速度测量最大值(m/s2)； Δpmax为接触表面压强最大变化量(MPa)；A1为常数，由剪切模量、材料密度等性能决定；α1、α2为加速度传感器经验参数(m/s2)，需要厂商进行提供。

1.4.2萨道夫斯基公式

在1.4.1中，通过实际测量值换算得到冲击波超压，进而通过萨道夫斯基算法，可以对其与TNT当量进行换算，萨道夫斯基公式如下：

(11)

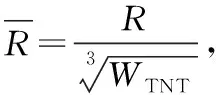
2 系统搭建与测试结果

2.1 测试设备埋设布局

图3所示为测试时炸点区及传感器埋设布局示意图，中心爆炸区为红色半径10 m圆形围成的区域，三角形所示为布设的加速度传感器，同心圆间隔2 m半径,夹角约120°。图4是测试系统框图。

图3 测试设备埋设布局示意图

图4 测试系统框图

2.2 测试数据与分析

2.2.1仿真测试结果对比

通过3组Ricker小波信号进行爆炸冲击波信号仿真，包括主频35 Hz、25 Hz和20 Hz三组反射信号和仿真频率衰减[19]，其中增加了0.3 W高斯白噪声。生成仿真波形如图5所示。

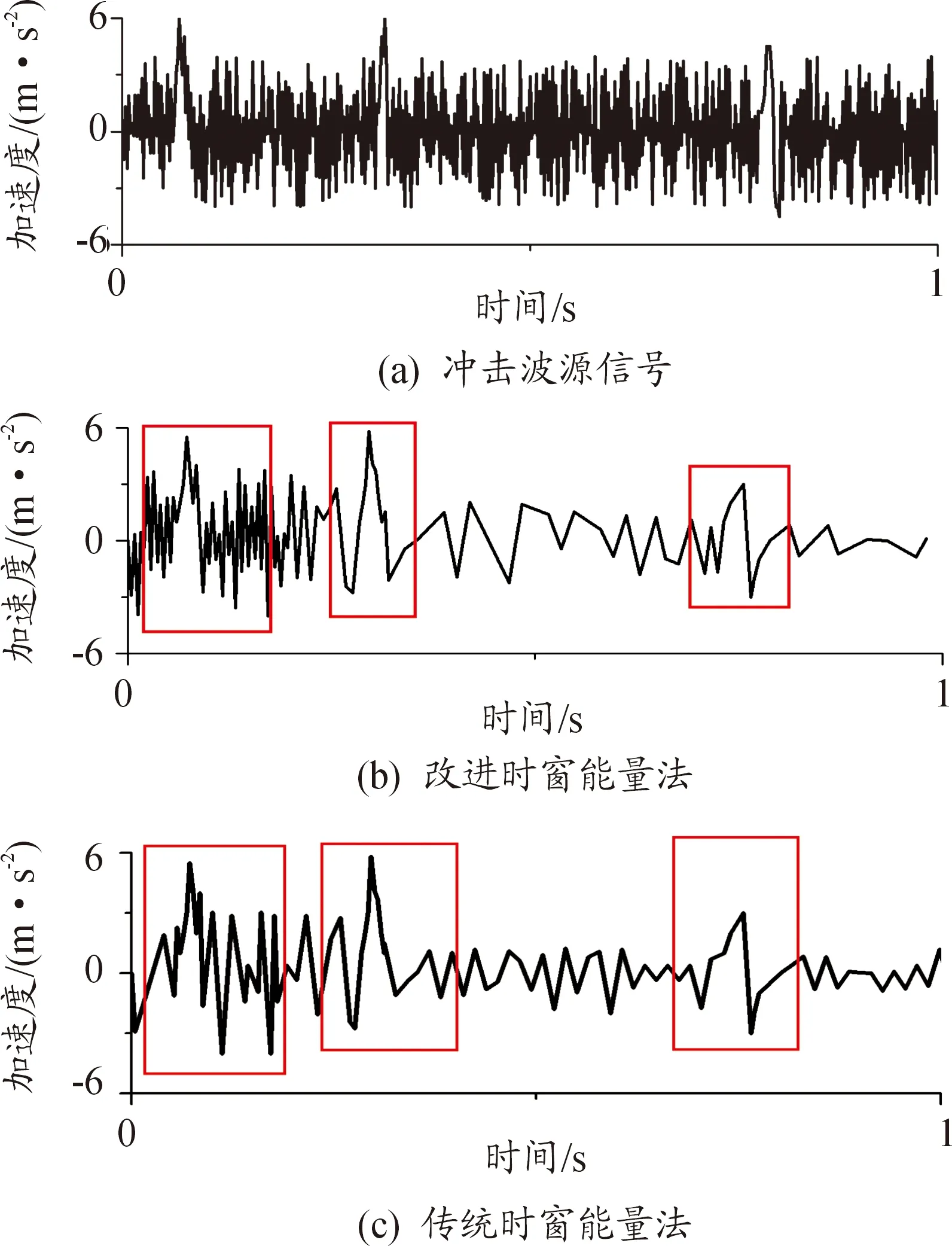
图5 源信号与不同方法提取的有效信号波形

图5(a)是添加了白噪声的源信号。图5(b)和图5(c)是滤波提取信号，三主频对应3个波峰。

图5(b)为改进时窗法提取的信号，采样时窗长为0.05s-0.1s。黑色线为信号波形，纵轴为传感器的路数，横轴为对应时刻，亮色为所选时窗。图5(c)是传统时窗法所处理信号并选取的时窗，该方法取定长时窗0.13 s。

对比图5(b)和(c)可知，第二、三峰值附近波形相似，仅第一峰值差异较大。图5(b)信号在第一小波峰即高频部分保持效果较好。而图5(c)信号中进行了滤波去噪，对原信号高频有效部分有明显削弱。由此可知，相较于传统时窗法而言，改进时窗法不但能够对信号低信噪比部分有效数据进行获取，也对高频部分保留和增强。

2.2.2冲击波实测效果对比

对11路冲击波信号采用两种方法采样，频率为1 000 Hz，采样时长为6 s。采样曲线如图6、图7所示，图6、图7分别为传统时窗法和改进时窗法的解析数据与时窗选择结果。 根据互信息量特性选取[2 2.5 3]、[3.5 4.5 5]、[5 5.5 6]三个初至时段。在该时段内，图5为1 s固定采样时窗所取波形，图6为改进时窗法分别选取0.7 s、1.5 s、0.8 s窗长解析所得波形。

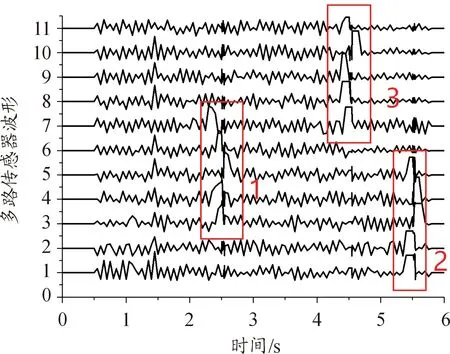
图6 传统时窗法采样曲线

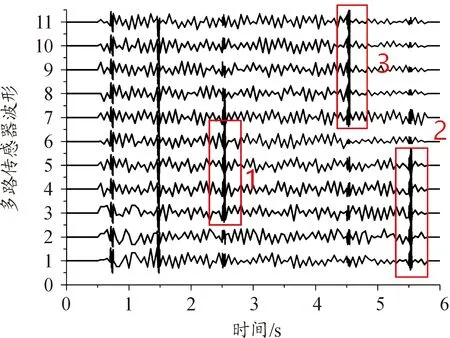
图7 改进时窗法采样曲线

图6中冲击波信号包括随机噪声，集中于框1、2、3中。噪声在整个图中分布使有效信号被抹去。从图7的数据中可得出结论，在1.3中利用改进时窗法去除高频噪声后，高频低信噪比有效信号得以保留，信号得到增强。

2.2.3实际测试数据

如表1所示是采样、换算所得数据。

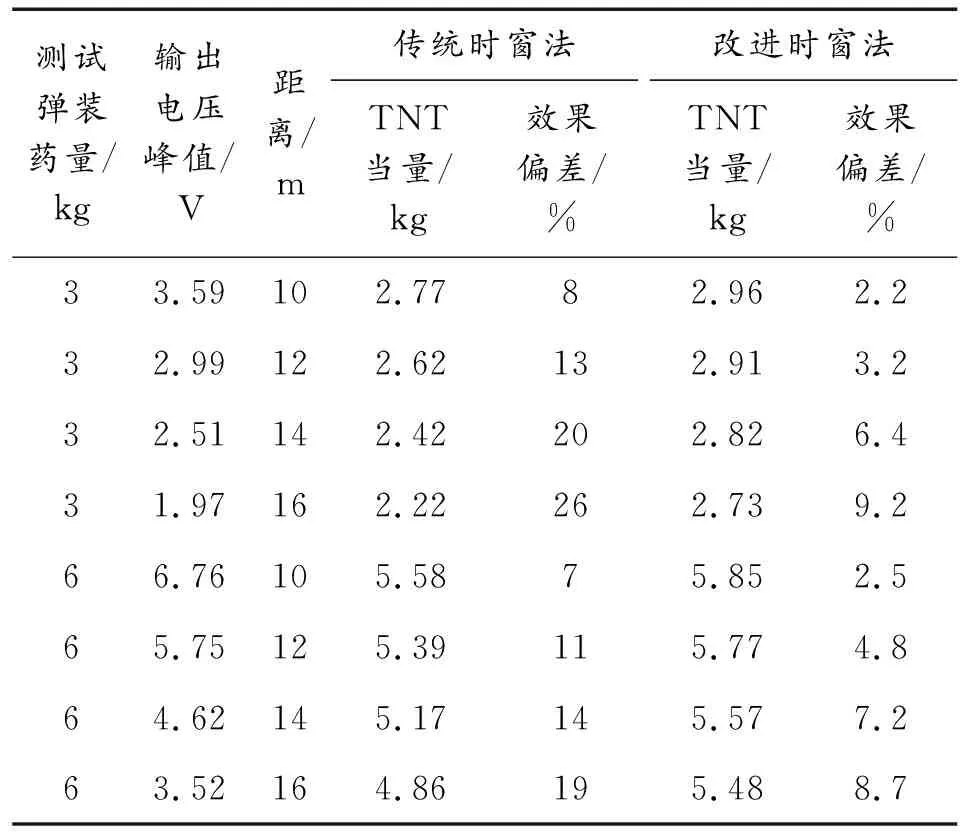
表1 测量数据

在有效半径范围内分别投放3 kg和6 kgTNT装药量测试弹，经过前端采集和上位机换算得出上表数据。通过以上数据表，可以看出在10 m、12 m、14 m、16 m位置使用传统时窗法的效果偏差均不小于7%，小部分甚至大于25%。

相较于传统时窗法，改进时窗法获取冲击波信号效果偏差降到10%以内，采样精度提升明显。

3 结论

1) 改进后时窗法通过在采集前端增加了峰值滤波，降低了信号失真水平。

2) 在时窗选择上，改进后时窗法结合Ricker小波信号实现变窗长选择时窗，实现有效信号保持和增强。

3) 系统将采样加速度有效值转换为TNT当量，满足监测数据直观性要求。