复合固体推进剂蠕变分析研究进展
强洪夫,冯帅星,杨正伟,王学仁
(火箭军工程大学, 西安 710025)
固体火箭发动机(solid rocket motor,SRM)在整个寿命周期里,其绝大多数时间都处于贮存状态,在贮存过程中,药柱在自身长期的自重作用下,将产生蠕变效应,使药柱下沉产生变形,特别是在固体火箭发动机立式贮存过程中,推进剂将一直承受较高应力状态下产生蠕变作用,如不采用适当措施,甚至会使固体火箭发动机药型发生明显变化,改变药柱的燃烧性能和安全系数。美国早在20世纪60年代就对民兵导弹进行了立式贮存研究[1],目前我国对固体火箭发动机立式贮存下推进剂的蠕变特性主要采用仿真的手段开展,对复合固体推进剂蠕变机理的研究较少。研究复合固体推进剂蠕变行为和蠕变机理对于固体火箭发动机的贮存结构完整性分析具有重要的意义。因此,本文从宏细观尺度分析了推进剂实验测试、蠕变本构模型的研究进展以及分析了复合固体推进剂蠕变机理,为固体推进剂的蠕变力学性能研究和损伤特性分析提供参考。
1 宏观蠕变测试方法研究
对复合固体推进剂宏观蠕变实验的研究主要为了研究其宏观变形与时间和应力之间的关系,研究表明,在等应力的作用下,拉伸蠕变平均比压缩蠕变大2至3倍(最大比值超过8)[2],因此,本节主要对复合固体推进剂的拉伸蠕变实验进行总结和分析,提出一种适合固体推进剂的拉伸蠕变实验方法。
1.1 力学性能测试实验
目前对复合固体推进剂的蠕变拉伸实验主要采用电子式或半电子式实验机和自行设计的纯机械式实验装置进行实验。
张永敬等[3]用INSTRON5500万能实验机对HTPB复合固体推进剂蠕变进行了研究,试件依据航天部标准QJ924—1985将复合固体推进剂制成哑铃型。电子万能实验机采用位移拉伸仪测量试件的形变,通过电脑控制系统输出数据,具有较高的精度。但在较低应力作用下实验所需时间较长、实验成本较大。
王永帅等[4]在装有无水氯化锂保温箱内并控制实验温度的温湿度,对复合固体推进剂进行了蠕变研究,加载方式为砝码加载,采用磁致位移传感器测量变形情况。王鑫等[5]通过对砝码加载和实验机加载进行了对比,验证了砝码加载可用于复合固体推进剂蠕变研究。周献刚等[6]根据不同应力水平对HTPB推进剂粘接界面进行了蠕变试验,试验仍通过挂载不同质量的砝码施加不同拉力载荷。但对测量区域的蠕变变形进行测量时采用画出标记线的方法标记出试件的观测区域,如图1所示,用调整好放大倍数的CCD摄像机通过测量每张图两道标记线的距离,可以较为准确地测量小型推进剂/衬层粘接界面试件的蠕变位移。采用挂重物的方式对拉伸蠕变进行研究并不能实现对材料的恒应力加载,目前保持恒应力的方式主要通过改变杠杆比例为基础进行设计的[7]。赵艳[8]对常规的蠕变试验机进行了改造,采用曲轴杠杆的方式加载以保证在实验过程中试件受力的恒定,改造后蠕变试验机示意图如图2。
1.2 当前研究中的不足和改进措施
目前虽然对复合固体推进剂的蠕变性能进行了,仍存在以下不足:
1) 由于蠕变过程时间较长,在采用电子万能实验机对复合固体推进剂进行蠕变研究时,成本耗费较大,采用机械式砝码的方式加载,则无法保证其在蠕变过程中恒定的应力状态,虽然目前已有相关学者对机械式蠕变实验机进行了改进[7-8],但对于不同材料和试样尺寸,仍需要设计和计算加载臂的尺寸,且加工精度要求高,加工困难。
2) 目前对复合固体推进剂蠕变的研究集中在对其单轴拉伸蠕变的研究,双轴和三轴等力学性能研究较少,而且对于固体火箭发动机而言,在贮存过程中伴随着固体推进剂的老化,目前研究并没有考虑推进剂的老化影响。
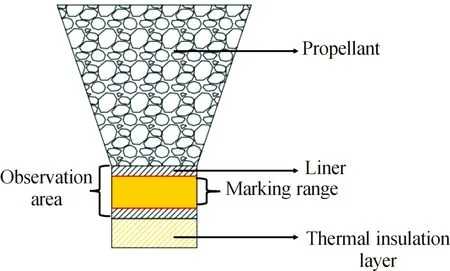
图1 固体推进剂粘接界面测试区域示意图

图2 蠕变试验机改造示意图
针对固体推进剂存在的蠕变时间长、变形测量困难及环境难控制的问题,可以设计多试件同时测量装置,采用划线或标点的方式标出测量区域,在老化箱内进行实验,用CCD相机协助进行测量,然后采用数字处理技术得到应变值。在对测量区域进行处理时,也可以采用数字相关技术对其蠕变过程中的形变进行研究,测量精度可达20 με[9]。在理论层面上,可以根据时温等效理论,采用较高的温度设计试验,通过理论换算,从而达到节约实验成本的目的。为了减少实验件的数量,还可根据Boltzmann叠加原理,在蠕变实验设计时,采用应力阶梯加载的方式进行加载。
2 细观蠕变测试方法研究
对推进剂的细观蠕变过程进行研究主要是为了研究在蠕变过程中推进剂的细观结构变化,从细观角度解释和推测推进剂的宏观变化,建立损伤本构来定量分析复合固体推进剂蠕变过程中的损伤情况。
2.1 细观静态观测实验研究
在对推进剂受载过程中的细观结构进行研究时,通常对其断面进行观测。如Knauss等[10]通过扫描电镜和图像分析的方法,对推进剂在老化作用下的裂纹扩展机理进行了研究,结果表明,扫描电镜可以对复合固体推进剂二维断面的裂纹进行较为清晰的观测。Collins等[11]采用微CT扫描的方法,扫描重构了固体推进剂的三维微观形态。Lee等[12]通过微CT扫描,研究了复合固体推进剂试件裂纹开裂及扩展情况。王亚平等[13]采用单轴拉伸和扫描电镜,研究了慢拉伸速率对复合固体推进剂拉伸性能的影响,曾甲牙[14]采用微型试件,通过扫描电镜对复合固体推进剂在拉伸应变状态下的断口微观形貌进行了观测,结果均发现,在低加载速率下主要表现为颗粒脱湿,断口上有很多裸漏的颗粒。对复合固体推进剂进行断口观测只能静态观测其断裂后的实验结果,无法对蠕变过程中的细观结构进行研究,因此需要采用动态观测方法对其蠕变过程进一步研究。
2.2 蠕变过程细观实验表征
采用静态观测方法可以研究推进剂蠕变过程细观结构变化产生的不足。如周水平等[15]采用原位扫描电镜对含GAP的复合固体推进剂单轴拉伸行为进行了分析,发现含GAP的推进剂的细观破坏由粘合剂基体拉丝、断裂以及粘合剂与固体填料之间的“脱湿”两种因素共同作用的结果。李高春等[16]采用原位扫描电镜与数字图像相结合的方法对准静态拉伸下不同变形阶段固体推进剂进行了电镜扫描,得到了推进剂细观表面变形场。由于蠕变过程和准静态过程具有相对接近的拉伸速率,因此准静态过程拉伸的细观变化可为固体推进剂的蠕变细观变化研究提供较为可靠的参考。
在固体推进剂蠕变过程中,其细观结构的损伤导致通过材料的声速发生变化,因此可以通过超声波测量变形过程中声速和声衰减等的变化对损伤演化过程进行定量分析。如Bescond等[17]用超声方法对固体推进剂拉伸加载过程的测量表明,弹性常数随应变的增加而降低。Knollman等[18]得到的固体推进剂在拉伸条件下声衰减系数随应变的变化曲线,如图3。可以看出,随着应变的增加,声速在不断衰减。Knollman等[19]认为推进剂声衰减和声速的变化主要是由于颗粒脱粘产生的孔穴引起的,于是在用超声测量推进剂的损伤演化的研究中,考虑由于颗粒脱粘和随后的孔洞生长产生的累积损伤,建立了基于超声波测量的细观损伤模型,将宏观的超声参量与细观损伤参数联系起来建立了相关模型。

图3 声速的衰减与应变的关系曲线
推进剂泊松比从不可压缩情况下的v=0.5变化到可压情况下v≠0.5时,泊松比对药柱结构分析会有特别严重的影响[20-21]。如郑健等[22]。在对固体推进剂蠕变过程中的泊松比变化研究时,采用对测量区域粘贴应变片的方式在QJ211B型电子试验机上对试件进行了泊松比测量实验。崔辉如[23]提出了一种新的考虑时间和温度相关泊松比的推进剂蠕变本构模型。陈鹏万等[24]研究了蠕变过程中应变和孔隙率的变化关系,并建立了泊松比与损伤相关模型。Hubner等[25]通过有限元细观力学计算,模拟了界面脱粘对含能材料泊松比的影响,并建立了泊松比与体积膨胀的关系。Ho等[26]、职世君等[27]分别基于蠕变实验数据和老化实验数据,得出了孔隙率与泊松比的计算公式。
2.3 当前研究中存在的不足和改进措施
目前对固体推进剂的细观静态观测方法主要有扫描电镜、微CT以及原位电镜等,间接观测方式主要有超声测量、泊松比测量等,在研究过程中仍存在以下不足:
1) 目前对固体推进剂研究较多的是对其断面进行细观结构的观测,无法控制试件断裂过程中的回弹而导致的微裂纹闭合,而且仅对其断面进行观测,并不能对固体推进剂的蠕变不同阶段的细观变化进行分析。
2) 通过间接方式如超声测量、泊松比等表征固体推进剂细观变化时,往往需要首先确定宏观表征变量与细观损伤表征参量之间的关系,建立准确的本构关系仍需要对其细观损伤表征参量进行统计分析。
在蠕变过程中的前两个阶段,很难采用接触式测量方式控制其对蠕变过程的影响,因此接触式测量方法对蠕变过程推进剂细观结构的观测不适用,可以通过间接测量的方式表征复合固体推进剂蠕变过程细观损伤的变化,比如声速测量、泊松比测量等;也可以设计适当的装置,在蠕变过程中,对固体推进剂试件选取不同的时间点控制其应变,然后用微CT中进行观测。
3 蠕变本构模型研究进展及蠕变机理的讨论
3.1 幂律本构模型及线性粘弹性模型
目前对复合固体推进剂蠕变过程较多地采用时间硬化理论和线性粘弹性模型进行描述。时间硬化理论最早由Kayahob[28]提出,该理论认为,在蠕变过程中蠕变率降低显示出材料硬化的主要因素是时间,即当温度一定时,应力、蠕变率与时间之间存在一定关系,有:
(1)

时间硬化理论可以较好地拟合推进剂蠕变过程前两个阶段的应变-时间关系[6]。在采用线粘弹性理论对复合固体推进剂蠕变过程进行描述时,胡义文等[29]采用Burgers模型对复合固体推进剂的蠕变前2个阶段进行了拟合。Burgers模型由Kelvin模型和Maxwell模型串联而成,如图4所示,蠕变模型为:
(2)
式中:EE、EVl分别为普弹模量和高弹模量;ηVl、ηVp分别是链段运动粘度和本体粘度;σ为施加的应力;t为蠕变时间。

图4 Burgers模型示意图
时间硬化理论和线性粘弹性本构模型虽然可以很好地描述复合固体推进剂蠕变过程的前两个阶段,但无法描述蠕变过程的第3个阶段。为了对复合固体推进剂的蠕变全过程进行描述,必须建立含有损伤的非线性本构模型。
3.2 非线性本构模型及损伤模型研究
目前常用的非线性蠕变模型有Leaderman非线性黏弹性蠕变模型和Schapery蠕变型非线性本构模型。Schapery蠕变型非线性本构模型为[30]:
(3)

(4)

(5)
式(3)~(5)中:D0和ΔD(ψ)分别是暂态蠕变柔量和增量;g0、g1、g2、aσ是应力相关的参函数。
张永敬等[3]基于蠕变实验,采用Schapery蠕变型非线性本构模型研究了丁羟复合固体推进剂的力学行为,研究表明,Schapery非线性本构模型可以较好地反映HTPB推进剂的力学性能。由于复合固体推进剂在蠕变过程的第三阶段损伤急剧增加,要想对复合固体推进剂的整个过程进行描述,必须考虑损伤的因素,目前常用的损伤本构有Kachonov损伤模型、Rabotnov损伤模型等。如Richard K等[31]针对固体推进剂材料,利用Kachonov损伤模型,计算了蠕变加载的损伤演化为:

(6)
式(6)中:D为损伤变量;σ0为恒定的应力;N为勒贝格应力范数;β为线性累积损伤指数;t为应力作用时间。
Richard K.Kunz等[32]阐述了线性累积损伤模型能够很好预测推进剂材料在各自载荷条件下失效,并提出了一种线性累积损伤演化模型参数的获取方法。Ho等[33]对HTPB/AP推进剂的蠕变损伤进行了研究,并采用线性累积损伤理论确定了固体推进剂的损伤程度。
3.3 复合固体推进剂蠕变产生机理的讨论
复合固体推进剂的蠕变行为具有明显的时间相关性及非线性粘弹性。如P.A Kakavas等[34]研究高氯酸铵增强推进剂复合材料的力学性能时发现,复合固体推进剂的蠕变主要取决于黏合剂的蠕变,高氯酸铵颗粒可以有效增加推进剂的模量。复合固体推进剂黏合剂作为高分子复合材料,其蠕变主要是分子链段沿外力的舒展使得高分子之间的粘滞阻力使形变和应力不能即刻达到平衡的结果。
固体推进剂用黏合剂的蠕变性能与自身分子链的大小、晶体结构以及形貌、结构组成密切相关。作用力是分子链运动的根源,因此,其蠕变速度与其所受的载荷密切相关。温度可以显著提高聚合物分子链的激活运动,同样可增加蠕变速度。胡义文等[29]对PBT基复合固体推进剂的高温蠕变行为进行了研究,结果表明,交联点增多,弹性模量增大,阻碍分子间链段运动的力增大,从而使复合固体推进剂的抗蠕变性能改善。
3.4 当前研究中的不足和改进措施
通过对复合固体推进剂蠕变本构模型的研究,发现目前对复合固体推进剂的研究大多基于宏观的蠕变行为进行研究,并未与复合固体推进剂蠕变过程内部结构变化建立宏细观尺度的构效关系;且目前的本构模型仅能描述复合固体推进剂蠕变过程的第一和第二阶段,无法描述蠕变整个过程。要解决这个问题,可以通过计算不同应力状态下蠕变最大时间和最大应变,引入损伤变量,对复合固体推进剂的整个过程进行描述。
从国内外学者对复合固体推进剂的蠕变机理研究上可以看出,复合固体推进剂的蠕变产生主要取决于黏合剂的蠕变,高氯酸铵颗粒可以有效增加推进剂的模量。在不同的载荷作用下,复合固体推进剂的蠕变行为差异较大,要深入研究复合固体推进剂的蠕变机理,必须采用宏细观试验对其蠕变力学性能进行较为全面的研究。
4 结论
1) 实验研究方面:① 借鉴其他粘弹性材料的蠕变实验方法,对复合固体推进剂的宏观蠕变实验加载方式、环境控制以及观测手段进行设计;② 根据时温等效原理和Boltzmann叠加原理对蠕变实验方法进行合理的设计;③ 借鉴复合固体推进剂在不同应变率加载条件下的细观观测方法,设计一种适合复合固体推进剂蠕变过程细观结构观测的实验方法。
2) 本构模型及蠕变机理方面:① 考虑损伤因素对复合固体推进剂蠕变整个过程的影响;② 通过引入损伤因子采用统一蠕变型损伤本构模型对不同应力加载下的蠕变断裂时间进行预测;③ 考虑机械应力和温度对蠕变影响的耦合作用,建立考虑温度和应力的统一的本构模型;④ 结合蠕变过程微细观实验,对其蠕变过程不同阶段蠕变机理和变化阈值点进行描述。

