从统计学史解析“自由度”概念
吕付华
(1.云南民族大学 社会学系,云南 昆明 650223;2.云南大学 公共管理学院,云南 昆明 650223)
可作为σ的最佳估值使用。费歇尔却
一、引 言
什么是自由度?在Fisher与Pearson(以下称费歇尔、皮尔逊)关于自由度的激烈争论尘埃落定80多年后[1-5],追问这一问题似乎有些不合时宜,但事实上直到现在,它仍是一个极为基本却在统计学教科书、专著以至相关论文中没有得到圆满回答的问题。在统计学三大分布(χ2、t、F分布)中,自由度是决定这些分布特征、性质最重要的参数。在列联表、回归与方差分析等统计方法中,自由度也是决定统计结果的关键变量之一。假若没有自由度概念,那么从样本统计量估计总体参数的统计过程必将在逻辑上缺失关键环节,在准确性上出现巨大偏差。而一旦弄错自由度的数目,则从三大分布的概率分布表中得到的将是错误的概率值,从而也必将错误解释相应假设检验的显著性。
费歇尔提出自由度概念之后,国外统计学界一直就如何一般化解释自由度进行探讨。Walker借助n维几何工具把自由度理解为样本统计量中观察值数目减去约束条件数目后的结果,但Good批评Walker不能在复杂情形下把所谓的约束条件解释清楚[6-7]。Cramer把自由度定义为二次型统计量的秩,但是因为这一定义涉及极为艰深的数学推理,它并不为一般统计学者所采用[8]379-381。即使 Good站在Walker与Cramer肩膀上提出了对自由度的简化理解,即自由度就是假设检验中检验包含于K中的假设H时的参数空间维度差异d(K)-d(H),后来事实也证明,它只不过是训练学生快速写出自由度的工具而已[7]。所以,一方面有学者如Pandey和Bright等抱怨教科书中充斥着各种各样使学生备感疑惑的自由度解释[9];另一方面,Good等学者也不得不承认无论针对学生还是统计学专家,自由度都是一个非常难于解释清楚的概念[7]。
相比国外,在国内有代表性的教科书中,陈希孺把自由度解释为三大分布中能够随意变化的变量值个数,并在附录中指出,若相关变量中有n个约束则自由度相应减少n个[10]95-104;陈家鼎等则只在有关定义、定理中提到自由度及其算法而未作特别解释[11]43-59。在极为有限的几篇专门讨论自由度的论文中,李友平认为自由度指一组数据中可以自由取值的个数,并以为统计量的“确定性”限制了与之相关的一组数据的“自由度”[12]。实践中,这些解释或能应用于简单条件下,可一旦涉及较复杂情形,如列联表中自由度的计算和理解,或者追问自由度与待估参数的本质关系,再或深究自由度的统计意义时,不难发现:以上解释不仅不能从根本上回答这些问题,而且往往导致相关专业师生对自由度的理解流于形式,以致自由度实际上成为了统计学中一个时常可见却又格外陌生的概念。
针对上述局面,Fienberg就皮尔逊与费歇尔在分类数据拟合优度检验上主要分歧的历史探讨为梳理自由度问题提供了基本线索[13]。Stigler对皮尔逊卡方检验推理逻辑和其理论错误以及费歇尔修正该错误的统计学史研究,则指出了深入理解自由度概念的根本路径[14]。陈希孺关于皮尔逊、费歇尔的统计学史研究也提供了有关自由度问题的广博数理知识和具体历史背景[15]213-246。借鉴这些成果,本文从统计学史角度,通过研究皮尔逊、费歇尔等人与自由度问题相关的原始文献,系统、深入、全面地拓展了已有相关解释,指出了Fienberg、Stigler论证过程中的不足之处,弥补了陈希孺主要依赖于Fienberg、Stigler及E.S.Pearson等人提供的二手资料以及论述不够清楚的缺陷。具体而言,本文包含了以下三个方面的分析:第一,皮尔逊是怎样论证卡方检验的理论逻辑,论证过程中出现了什么样的错误判断;第二,皮尔逊的错误判断是如何在统计实践中被发现的;第三,费歇尔通过自由度修正皮尔逊错误的理论、方法根据何在,怎么理解并以当代术语阐释这些根据。
二、皮尔逊与卡方检验
皮尔逊卡方检验曾被美国统计学史专家Hacking评为20世纪科学技术所有分支中20个主要发现之一,因为它不仅在实用上提供了检验已知数据和某个给定假设是否一致的极其简便的标准,还在理论方面成为了后继相似检验的先驱[16]。不过,在皮尔逊这一对现代统计学里程碑式贡献的原始论证中,却存在着一个不小的错误。
(一)皮尔逊(χ2,p)检验思路
1900年,皮尔逊在其标志性论文中提出[4]:假设对一个呈多项分布的k维正态总体进行随机抽样实验,得到的所有样本的频次分布在n+1个间格内,如果每个间格分别有变 量 值m1′,m2′,…,mn′,mn+1′;变量值m1,m2,…,mn,mn+1;以及变量值ms1,ms2,…,msn,msn+1。其中m′= 每个间格的 观 测 频次;m=每个间格预先假定理论频次;ms= 每个间格从样本数据中推断出的理论频次。
皮尔逊认为,在上述频次分布中,只存在着一个限制,即:∑m′=∑m=∑ms=N=样本大小。尤其重要的是,如果误差e=m′-m,则有e1+e2+…+en+en+1=0。因此他认为,n+1个误差中只有n个是自由变量,当前面的n个变量已知时第n+1个就能确定。由此,经过一系列推理,皮尔逊得到:
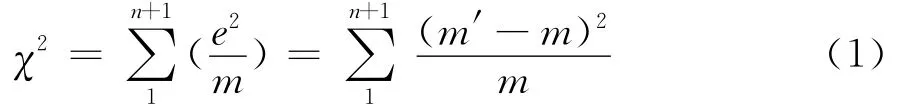
作为刻画n+1个间格中的实际观测频次和预先假定理论频次拟合程度的统计量,显然,χ2越小,说明观测频次与理论频次越一致。
进一步,皮尔逊证明,如果预先假定的理论频次是正确的,那么,随着样本大小N的无限增长,用式(1)得到的χ2统计量的抽样分布将完全独立于假定理论频次的概率分布,从而服从皮尔逊Ⅲ型分布(Γ分布),记为:

其中n′=n+1是样本间格数,并且该分布除χ2统计量外唯一决定因素就是n′。
皮尔逊随后断定,如果记大样本条件下由随机抽样导致的χ2为χn2′,由样本实际观测值与理论值算出的χ2为χ20,那么统计学家能够得到的样本由于随机抽样原因导致抽样误差大于或等于实际观测中观测值与理论值之间差异的概率将为:

鉴于式(3)不易计算,经由简化,皮尔逊又导出了两个更为当时的统计学者频繁使用的公式,即如果n′=n+1为奇数,将有:
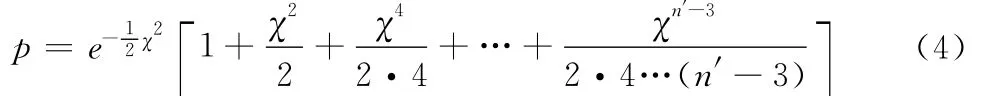
如果n′=n+1为偶数,则有:
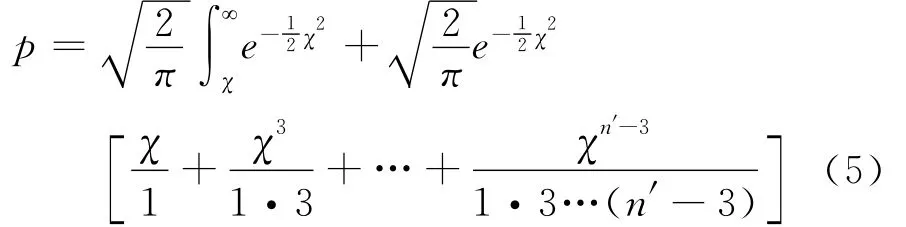
因此,实际操作中只需通过式(1)计算出χ20,再由n′的奇偶选择相应式(4)或式(5)代入χ0算出p值,就能得到在预先假定的理论频次正确条件下,随机抽样出现χ20这么大差异或更大差异的可能性有多大的判断。毋庸置疑,p值就是皮尔逊所谓的衡量样本观测频次与其假定理论频次之间拟合优度的标准,它介于(0,1)之间,并与χ20成反比,χ20越小,则p值越大,说明样本观测频次与理论频次之间的拟合度愈好,也说明预先假定的理论频次愈为可靠。所以,它也被称为皮尔逊(χ2,p)检验。
(二)应用实例与χ2表
按当时惯例,皮尔逊还以实例对上述思路进行了具体说明。以同事 Weldon实际观察到的骰子投掷实验结果为例,经整理他得到表1数据[4]。

表1 皮尔逊卡方检验数据表
表1中,理论频次m1按Weldon最初设想的二项式理论分布26 306×(1/3+2/3)12算出。而在皮尔逊对实验结果检查之后,他发现12颗骰子同时掷26 306次,5点或6点出现的总和值是106 602次。于是,皮尔逊用106 602取代用概率1/3得到的理论值105 224,得到新概率值0.337 7,然后用26 306×(0.337 7+0.662 2)12的二项式理论分布算出理论频次m2
。因为n′=n+1=13,通过式(1)和式(4),可轻易得到:按理 论频次m1,χ2= 43.872 41,p=0.000 016;而按理论频次m2,χ2=17.775 755 5,p=0.122 7。皮尔逊这样表述实验结果:对于前者,p=0.000 016=1/62 550说明,如果作62 550次随机实验,只有1次实验由于随机原因导致的系统偏差会大于或等于实验观测到的样本观测频次与理论频次的偏差,其余62 549次实验所得系统偏差都将小于实验观测偏差,这是一个极少见的小概率事件,它在实验中出现将使人们不得不怀疑由26 306×(1/3+2/3)12所得理论频次的正确性;对于后者,p=0.122 7≈1/8表明,8次随机实验中就有1次实验由于随机原因导致的系统偏差大于或等于实验观测到的偏差,这已经在可以接受的范围内。因而,实验结果证明,使用二项分布(0.337 7+0.662 2)12去拟合实际观测数据将比(1/3+2/3)12更可靠。这也说明,可以否定实验中骰子是均匀的,其每面出现的概率均为1/6,而接受骰子均匀度有偏差的假设。
考虑到卡方检验的应用前景,皮尔逊和他的学生Elderton还制作了现代统计学史上第一张标准的χ2分布表[17]28。
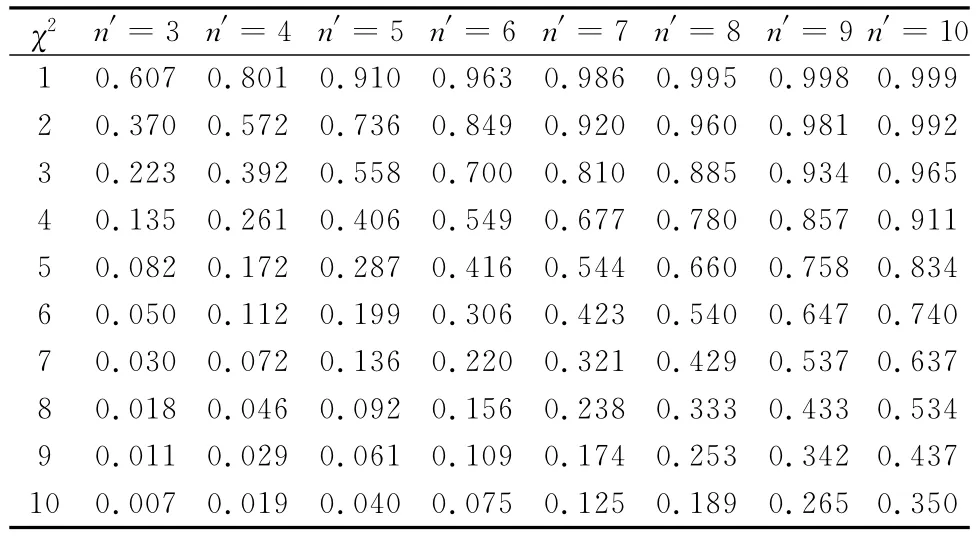
表2 Elderton标准χ2分布表
可明显看出,在假定随机抽样所得样本的理论频次已知(即抽样总体的分布已知)条件下,(χ2,p)检验的决定因素在于n′的数量,且n′=n+1。
(三)皮尔逊的错误判断
在皮尔逊卡方检验构想中,总体的理论概率都是假定预先已知的,但实际中很多案例并不如此,总体理论分布未知并需要从样本中进行推断反而更常见。皮尔逊也意识到了这个问题,但遗憾的是,他做出了一个错误判断。
上文提到,皮尔逊视随机样本中的m′为每个间格的观测频次,m为每个间格预先假定的理论频次,ms为每个间格从样本数据中推断出的理论频次。他特别声明,如果记m=ms+u,则在大样本条件下,原则上,比率u/ms将很小[4]。


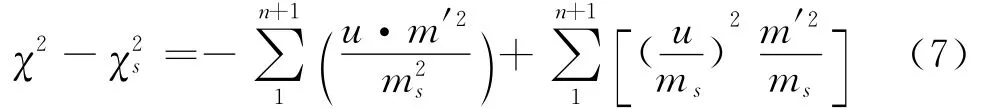
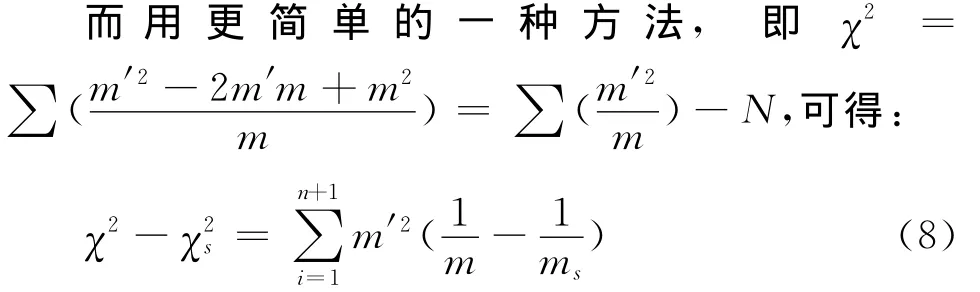
皮尔逊对式(6)有两个重要判断:第一,等式后左边第一项要么是负的(因而可以与第二项部分抵消),要么是很小的正数。第二,等式后第二项虽然为正,但在任何情况下它都将很小,因为它包含了每一个被加总的)2。因此,在这两个判断支撑下,皮尔逊断言,χ2与χs2相差不大,在大样本条件下,χ2与χs2应有同一极限分布。

客观而言,皮尔逊错误判断的后果并非微不足道。在 Weldon骰子实验中,n′=13与n′=12意味着p值接近0.05的差异,这已经非常显著了。而在列联表中,皮尔逊错误判断的影响更为突出,如后文所述,皮尔逊认为2×2列联表的n′=4而非2,3×3列联表的n′=9而非5,在假设检验中这必将导致灾难性的结果。
客观地说,皮尔逊卡方检验仍是现代统计学史上最伟大的发现之一,它是第一个也是最重要的一个沟通了描述数据分析与推断数据分析的检验准则。皮尔逊用公式分离、表达出了另一个重要问题,以至于20年后另一个天才用他自己简单的方法做出了一个巨大发现 —— 自由度。
三、卡方检验的准确性问题
或许是皮尔逊对χ2与χ2s相差不大的论证过于隐晦,在卡方检验提出后的20多年里,大多数统计学家即使错误地使用了卡方检验也往往毫无察觉。但也有例外,Greenwood与Yule就在反复检查、比对收集到的大量数据后,对卡方检验的准确性产生了疑问,这种疑问在他们对四格表(2×2列联表)的分析中更是达到了顶点,并成为了费歇尔讨论自由度问题时最重要的论据。然而,Stigler对此仅一笔带过,Fienberg也对细节囫囵吞枣、含糊其辞[13-14],所以,对此问题有必要重新细致梳理。
(一)Greenwood与Yule的发现
按皮尔逊的看法,如果对形式为表3的四格表中两属性相关问题进行研究,首先必须利用χ2统计量考察p值,以检验两属性间是否相互独立[17]27-30。

表3 一般形式的四格表
具体而言,皮尔逊认为,最好的方法就是应用统计量:

代入Elderton表找到相应p值,如果p值很大,则说明观测频次与预先假设的两属性间相互独立的理论频次相当拟合,也就表明两属性相互独立的假设成立。不过,皮尔逊认为,虽然四格表中的理论频次是由样本观测频次推断而得,但在卡方检验中,它和理论频次事前已知差异不大,所以代入Elderton表匹配相应p值时,n′=2×2=4。
Yule作为皮尔逊的学生,他对皮尔逊卡方检验的思路十分熟悉,在1906年对一个3×3列联表进行检验时,他依然使用n′=3×3作为(χ2,p)检验的n′值。直到1915年,他才在对四格表的分析中透露出了自己的不同看法。
这一年,Greenwood与Yule考察了欧洲大陆针对伤寒和霍乱进行接种预防的大量数据[18]。为了弄清楚接种是否能够预防霍乱和伤寒,他们把收集到的数据整理为表4的形式。
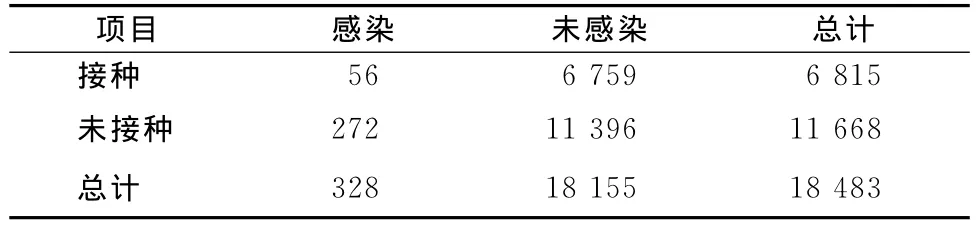
表4 欧洲伤寒、霍乱接种实际数据表
如果依照皮尔逊的方法,则首先应用式(9)算出χ2统计量,再按n′=4,找到相应p值,就可以判断接种和感染之间是否相互独立。例如表4中可得χ2=56.23,p小于0.000 1,说明接种与感染之间有显著相关。不过,虽然Greenwood与Yule有保留地承认皮尔逊(χ2,p)方法能够为这些数据提供有效的判定标准,但在反复检验和比较后他们发现,如果按照皮尔逊的方法,四格表中的χ2统计量必然服从n′=4的卡方分布,也即必然有:

而按照他们的理解,设p1=a/(a+b)= 接种感染的人/所有接种的人,p2=c/(c+d)=未接种感染的人/所有未接种的人,那么统计量(p1-p2)/σp1-p2也能够为判定两属性之间相互独立提供同样标准。进而,假设表3中A、B两因素相互独立,则必然有p1=p2= (a+c)/N,这样一来,他们发现:当四格表中的N充分大时,按棣莫弗 — 拉普拉斯中心极限定理,统计量
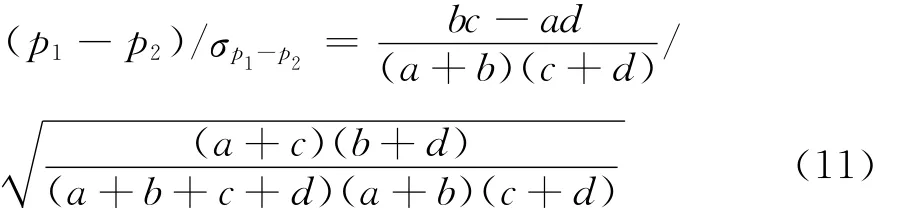
必将渐进于标准正态N(0,1)。而使他们疑惑的是,如果对式(11)取平方,则有:

显然,由于式(11)中统计量服从N(0,1),则式(12)中χ2统计量的分布必服从以下公式:

毫无疑问,式(13)等价于把n′=2代入皮尔逊卡方检验所得之结果,而非式(10)代入n′=4的结果。所以,Greenwood与Yule在文中多次指出,他们和皮尔逊之间就列联表的独立性检验存在着不同的看法[18]。
但是,Greenwood与Yule在1915年并未意识到他们上述发现的意义,也没有对他们和皮尔逊在列联表卡方检验上的分歧实质给出进一步说明。他们仅仅宣称,用皮尔逊卡方检验得出的因为随机抽样导致的任何可能事件或不可能事件的概率,总是大于用其他方法检验出的概率,因此,必须谨慎使用卡方检验。总之,他们在当时回避了困难,这种局面直到费歇尔提出自由度概念以后才得以彻底改观。
四、自由度与费歇尔对卡方检验的修正
在现代统计学史上,费歇尔是继皮尔逊之后的又一个巨人,费歇尔对现代统计学有着多方面的贡献,其中就包括他利用自由度概念对皮尔逊卡方检验错误的修正。费歇尔的修正过程,不仅集中体现了其出色的数学直觉与通过个案一般化重要问题的思想风格,也使自由度的本质含义和其蕴含的统计思想淋漓尽致地体现出来。
(一)自由度与n维几何
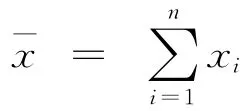
可作为σ的最佳估值使用。费歇尔却
费歇尔认为,利用n维几何的直观方法,可以把样本(x1,x2,…,xn)视为n维欧几里得空间Rn中的一点,统计量的除数之所以为n,在于确定珚x时,由于没有任何独立约束,点(x1,x2,…,xn)可以在n维空间中自由活动。而统计量s的除数应为n-1的理由在于,确定s的前提是珚x已经确定,这意味着点(x1,x2,…,xn)将受到一个独立约束(xi-)=0。因此,点(x1,x2,…,xn)就只能在一个通过点(x珚,x珚,…,x珚)的n-1维超平面上活动,统计量s只有n-1个自由度。以三维为例,样本(x1,x2,x3)可以看成是以总体均值为原点的3维空间中的一点,确定x珚时,由于没有任何限制,点(x1,x2,x3)可在3维空间中任意活动,而一旦确定,也就意味着3维空间中必存在一点A(),使得(xi-)=0。显然,一旦有了这个独立约束,点(x1,x2,x3)就不可能再在3维空间中自由活动,而只能在一个2维平面上活动了,因此,计算统计量s时就只有2个自由度了。
(二)列联表卡方检验中的自由度
有了自由度与n维几何工具,费歇尔对Greenwood与Yule在列联表卡方检验中发现的问题进行了新的思考[1]。他开宗明义地宣称:在每个间格的观察值都很大的条件下,卡方检验毫无疑问具有普遍效力,不过,当列联表卡方检验的理论频次需要从样本观察频次中推断出时,必须对n′的取值进行修正。进一步,费歇尔认为,在r×c列联表中,Elderton表虽仍然适用,不过,必须用自由度的数目加1,即n′= (r-1)(c-1)+1取代皮尔逊认为的n′=rc代入列联表进行卡方检验。


由度。而且,因为有eij=0,i=1,2,…,r以及=0,j=1,2,…,c,故还有r+c个约束条件,但由于行误差总和为零与列误差总和为零的限制,其中只有r+c-2个是独立的。因此,r×c列联表独立性检验中的χ2统计量的自由度应为rc-1-(r+c-2)= (r-1)(c-1)。
(三)卡方检验的前提假设
不料,费歇尔的文章一经发表,就遭到了来自各方的猛烈攻击。不仅皮尔逊曾轻蔑地说:“我希望我的批评者原谅我把他比作与风车作战的堂吉诃德”[5]。而且很多批评者认为,费歇尔对n′=2的修正适用的是这样的四格表[19]:牌局中甲、乙两选手各拿由26张红花色牌和26张黑花色牌组成的52张牌中一半,在红花色牌和黑花色牌期望频次均等条件下,问实际观察中出现如下频次(表5)的概率是多少?

表5 由挑选样本构成的四格表
显然,利用式(1)可得χ2=16/13,又因为表5中有独立约束条件m1=m2=m3=m4=13,以及e1=2=e4、e2=2=e3,所以有1个自由度。把n′=2代入式(5),最终可得p=0.27。
批评者认为,只有出现表5这样的非随机样本,卡方检验中的n′才需加以修正,而在表4那样他们称之为可疑个案的四格表中,无需修正n′=4。
针对这一批评,费歇尔指出了暗含于卡方检验中的三种假设前提(见表6)[2]。

表6 卡方检验的三种假设前提表
表6中,A代表着卡方检验中的理论频次在检验前预先已知的类型,在这样的前提下,1900年皮尔逊定义的、被多数统计学家代入Elderton表的n′无需做任何修正。皮尔逊利用预先已知的理论概率1/3对骰子实验结果的证明就属于这种类型。
B代表虽然总体的理论频次预先已知,但样本却非随机样本而是挑选样本,因此,代入Elderton表的n′需要修正。批评者对如表5那样的个案的讨论属于这个类型。
在费歇尔看来,卡方检验中真正重要的是C所代表的类型,它是实验、观察中最频繁出现的类型。其中理论频次必须依靠样本的边缘和进行人为计算,所以和B一样,必须对n′加以修正,Greenwood与Yule对四格表的检验就是典型。
费歇尔指出,就表3而言,他和皮尔逊分歧的实质在于:若设a,b,c,d所对应的概率为p1,p2,p3,p4,则必有p1+p2+p3+p4=1,如果两变量间相互独立,则p1p4=p2p3,假设从总体中抽取了N个样本,那么a,b,c,d必然服从如下多项分布:

显然,只要知道p1,p2,p3,p4和N,a,b,c,d的联合分布就将确定,任何关于a,b,c,d关系的函数分布也将确定。依皮尔逊的思路,在p1,p2,p3,p4预先已知的前提假设下,a,b,c,d相应的函数关系应为:



此时,必须把代入独立性卡方检验的n′修正为n′=2。其实,对费歇尔最有利的是Yule的实验结果。根据随机模拟方法,Yule获得了350个四格表的实验结果[20]。费歇尔把这些数据加以整理得到表7。得到函数关系为:

表7 Yule实验数据表
表中第2列得到的结果表示χ2值落入相应标示区间的实际观察频数,第3和第4列表示χ2值服从n′=2、n′=4的卡方分布时应有的理论频数。一目了然,n′=2时观察值与理论值的符合程度远胜n′=4,这证实了费歇尔的判断。
(四)最大似然估计法下的自由度
费歇尔认为,无论是基于直觉的n维几何证明,还是对不同前提假设的分析,都缺乏坚实的数学基础。于是,利用其1922年提出的最大似然估计方法,费歇尔对自由度问题做出了总结性的分析[3]。
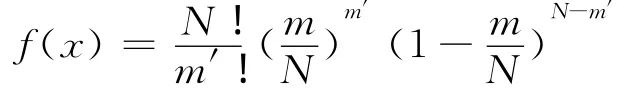


然而,当研究目的不在于直接得到m(),而是要对包含有m(θ)的χ2统计量的有效性进行判断时,情况又有所不同。此时,应该取什么样的χ2估计量作为含有参数真值的χ2的最佳估计呢?费歇尔以为,在这种情形下,应该以最小χ2为原则,取使
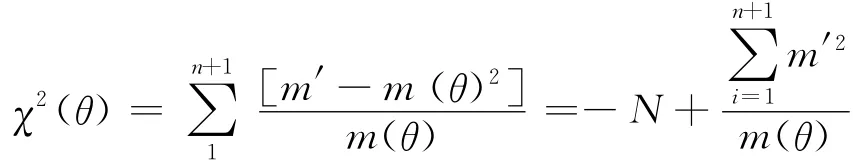
最小的χ2()作为最佳估计。理由很明显,作为刻画由于随机原因导致实际观察值与其理论概率值偏差程度的统计量,当取得最小χ2值时,说明此时χ2值中包含的m(θ)将最接近总体真值。因而,在诸多χ2(θ)的估计中,如果χ2()是其最佳估计,那它必然是关于θ的函数χ2(θ)的最小值点。又根据可微函数达极值的必要条件可得:
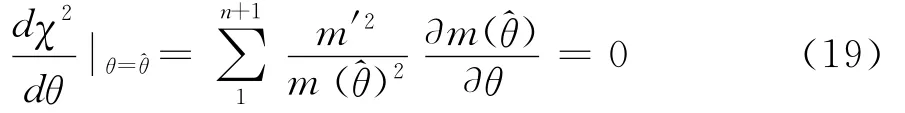

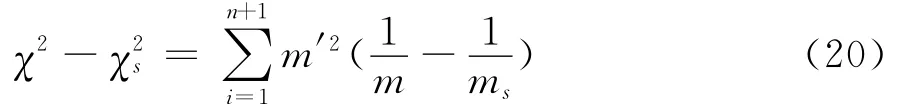
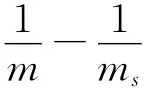

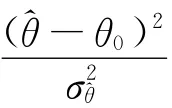
回到实际案例中,事实将更为明显。在1925年首版的《研究工作者用的统计方法》中,费歇尔对表1进行了新的解释。已知在表1中,皮尔逊利用样本观测数据估计了5点或6点出现的概率为0.337 7后,其代入卡方检验的n′仍然是n′=n+1=13。而费歇尔认为,因为0.337 7是从样本中估计出来的一个总体未知参数,因此代入卡方检验的n′必将失去一个自由度,也即应该用n′=12进行同样的检验。
3.小结。同一时期,费歇尔还利用自由度概念详细讨论了t分布和F分布(当时费歇尔考虑的是统计量logF的分布,即z分布),初步奠立了三大分布的数理逻辑基础。这些工作不仅在数理统计学界影响巨大,它们还成为了经济学、社会学等社会科学学科定量研究思想、方法的重要源泉,自由度概念也由于三大分布的广泛使用深入人心。随着20世纪30年代后统计学的高速发展,对那些不熟悉现代统计理论的基础文献,或者是从教科书中了解它们的人来说,自由度概念的实质及其蕴涵的统计思想却变得越来越陌生和难于理解。
五、结 论
基于第一手文献资料,从统计学史角度,本文厘清了皮尔逊在其卡方检验原初构想中的判断错误,探讨了这一错误的发现过程,细致阐释了费歇尔创造自由度概念修正该错误的数理逻辑。研究表明:
第一,Walker、Cramer与Good提出的三个被广泛引用的一般化经典解释,实际来源于他们对费歇尔原始论证的理解和抽象,但这三个解释都只选取了费歇尔全面论证中的一个方面。
第二,本质上,自由度是从样本统计量估计总体参数时的一次逻辑飞跃。因此,自由度可理解为样本统计量中排除了待估总体参数影响后仍能自由取值的随机变量个数。所谓独立约束条件,本质上就是待估总体参数。
第三,费歇尔与皮尔逊的自由度之争,并不是简单的概念争论,背后体现的是那个时代人们从描述统计走向推断统计时,对现代统计方法的创造性发明,以及围绕这些方法进行严格逻辑推导、实验说明和数学论证,从而奠定统计学沿用至今的理论基础的思维过程。
最后,在当前有关数理统计学史的中文专著、论文极为稀缺,而相关学科师生迫切希望了解统计学中一些基本概念、方法与思想的历史源流和演变发展背景下,笔者期望本文能抛砖引玉,以使统计学史研究引起人们更多重视。
[1] Fisher R A.On the Interpretation ofχ2from Contingency Tables,and the Calculation[J].Journal of the Royal Statistical Society,1922,85(1).
[2] Fisher R A.Statistical Tests of Agreement between Observation and Hypothesis[J].Economica,1923(8).
[3] Fisher R A.The Conditions Under Whichχ2Measures the Discrepancy between Observation and Hypothesis[J].Journal of the Royal Statistical Society,1924,87(3).
[4] Pearson K.On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is Such that It can be Reasonably Supposed to have Arisen from Random Sampling[J].Philosophical Magazine,1900,50(5).
[5] Pearson K.On theχ2Test of Goodness of Fit[J].Biometrika,1922,14(1/2).
[6] Walker H M.Degrees of Freedom [J].Journal of Educational Psychology,1940,31(4).
[7] Good I J.What are Degrees of Freedom[J].The American Statistician,1973,27(5).
[8] Cramer H.Mathematical Methods of Statistics[M].New Jersey:Princeton University Press,1961.
[9] Pandey S,Bright C L.What are Degrees of Freedom [J].Social Work Research,2008,32(2).
[10]陈希孺.概率论与数理统计[M].北京:科学出版社,2000.
[11]陈家鼎,孙山泽.数理统计学讲义[M].2nd.北京:高等教育出版社,2006.
[12]李友平.关于社会统计中"自由度"概念的解析[J].统计与决策,2007(12).
[13]Fienberge S E.Fisher's Contributions to the Analysis of Categorical Data[C]∥Fienberg S E,Hinkley D V R A Fisher,An Appreciation.New York:Springer,1980.
[14]Stigler S M.Karl Pearson's Theoretical Errors and the Advances they Inspired[J].Statistical Science,2008,23(2).
[15]陈希孺.数理统计学简史[M].长沙:湖南教育出版社,2002.
[16]Hacking I.Trial by Number[J].Science,1984,84(5).
[17]Pearson K.Tables for Statisticians and Biometricians[M].London:Cambridge University Press,1914.
[18]Greenwood M,Yule G U.The Statistics of Anti-cholera and Anti-typhoid Inoculations,and the Interpretation of such Statistics in General[J].Proceedings of Royal Society,Medicine(Epidemiology),1915(8).
[19]Bowley A L,Connor L R.Tests of Correspondence between Statistical Grouping and Formulae[J].Economica,1923(7).
[20]Yule G U.On the Application of theχ2Method to Association and Contingency Tables,with Experimental Illustrations[J].Journal of the Royal Statistical Society,1922,85(1).

