基于函数性视角的经济数据分析——以主微分分析方法为例
剡亮亮
(上海财经大学 金融学院,上海 200433)
一、引 言
金融市场中,经常会遇到高维数据、缺失数据以及样本观测点不规则分布等特殊的数据类型,已有的插值等技术在一定程度上解决了这种问题,但插值的缺陷在于只是从局部角度填充缺失值,缺乏充分的理论依据。本研究介绍一种新型的分析方法——函数型数据分析。研究过程中,尽管只能观测到数量有限且不规则的离散数据,但可以将其看作以时间为自变量的函数型数据。Ramsay首先提出函数型数据的概念以及函数型数据分析(FDA)的研究思路和方法。FDA的基本特征是把数据看成一个完整的函数对象,而不是个体观测值的简单排列。相比于传统的数据分析方法,FDA的优点在于:第一,可以实现对高维甚至无限维数据的分析;第二,较少的假定条件与较弱的结构约束,只需假定函数的光滑性;第三,不要求不同观测对象的观测点与观测次数相同;第四,通过对函数型数据不同阶微分曲线的分析,探索数据的动态变化特征等。
目前对函数型数据分析方法的研究,主要集中于主成分分析、聚类分析等因子分析方法,如严明义主要介绍了函数型数据的基本处理方法[1],讨论函数型数据分析方法在处理经济面板数据中的优势[2],靳刘蕊综述性的介绍了函数型数据中的主成分分析、聚类分析等方法并对国内宏观数据进行了分析[3]。上述方法基本是对传统多元统计分析方法的拓展,本研究中引入函数的泛函特征分析方式——主微分分析方法,即寻找一个微分方程去匹配噪声数据以使它能反映出曲线族的特征或者曲线的变化特征。将微分方程作为建模对象,不仅体现了函数线性模型的特点,同时也将主成分分析的理念融入其中。这是因为,微分方程既能反映曲线的变化趋势,又能捕捉到数据的梯度、曲率等特征。同时,微分方程解的集合是由基础解系张成的函数空间构成,它也能够为观测值变化过程进行建模,在这种意义上,它又具有主成分分析的理念,即能够找到一个函数子空间捕捉曲线族的主要变化特征[4]。相关的研究包括,Ramsay首次提出函数型主微分分析,并介绍了相关的处理方法[5],Poyton等采用迭代方法对主微分分析方法系数估计进行研究[6]。上述研究主要集中于主微分分析方法的理论分析与处理方法的拓展。也有针对主微分分析方法运用的研究,如Ramsay和Ramsey运用主微分分析方法对非耐用消费品指数进行了研究[7],叶振军等运用主微分分析对时变参数N-S期限结构模型进行研究,分析了时变参数N-S期限结构背后的运行机理[4]。纵观国内外对主微分分析的研究,基本集中于运用主微分分析提取函数空间中的主成分因子,未涉及主微分分析效果判断,拟合微分方程基础解系的特征,解函数与原数据及原拟合函数的关系等研究。笔者在应用主微分分析方法的基础上通过对全国银行间同业拆借利率的分析实现了对上述问题的研究并得到较为理想的结果,另一个贡献点则在于发现主微分分析方法在处理不规则观测数据时的优势。
二、主微分分析模型
函数型数据分析的主要观点是我们观测到一个连续可微过程的离散数据
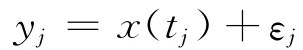
其中,{yj}是观测到的离散数据序列,x(t)为潜在的一定阶数可微的连续函数,εj则表示不可观测的误差成分。为了得到对 {yj}较好的拟合且一定阶可微的光滑函数x(t),我们需要运用特定的惩罚函数。比如,我们希望得到的函数具有光滑的两阶导数,根据规则可选取拟合函数的光滑四阶导数作为惩罚函数[8]160-200,得到如下的拟合标准:
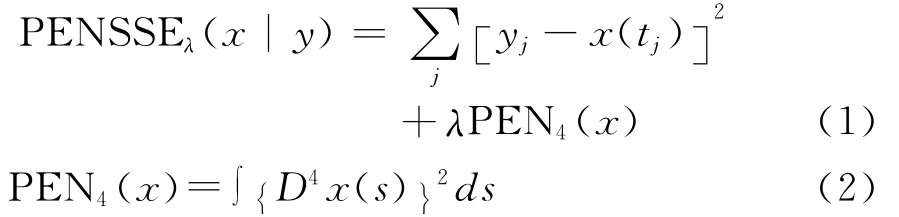

其中,φk表示一组固定的基函数集(可以为常数基,Fourier基,B-Spline基等),cjk为每个基函数对应的系数。
首先,考虑齐次的情况,即没有外界的扰动函数存在。找到尽可能与线性微分方程对应的算子L,使得

为了达到目标,我们必须估计方程(4)中的m个系数βi,i=0,1,…,m-1。当然,这些系数中有些是常数,甚至取值为0,常系数的情况可以通过引入常数基而包含在式(5)所述系数结构中。
由于我们希望算子Lxi尽可能的消除已给的数据函数xi的影响,笔者将函数Lxi当作相应的线性微分方程(如式(4))的拟合残差。利用最小二乘法定义拟合残差函数Lxi的标准:
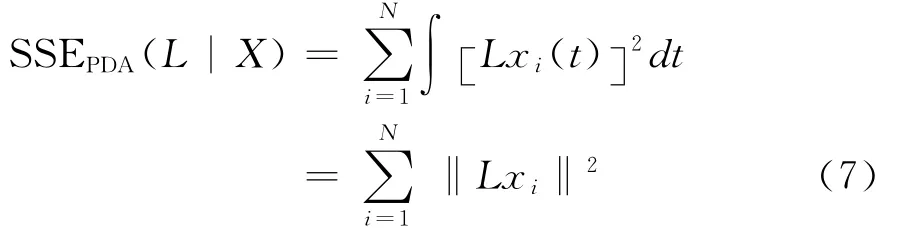
其中,λ为惩罚因子,可通过广义交叉验证法(GCV)得到。至此我们可以解得平滑可微函数x(t)。从拟合过程可知,部分的数据缺失并不影响拟合结果。
引入微分算子来讨论平滑标准,首先定义一个线性微分算子
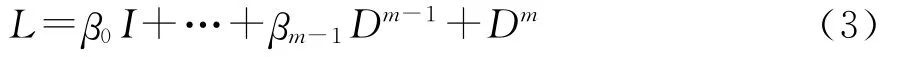
则与之相对应的微分方程为

其中,βi(i=0,1,…,m-1)表示微分算子系数,可以近似的表示为:
如果对于每个函数xi均存在一个与之对应的外界扰动函数fi
,则微分方程为

此时,最小二乘拟合的标准变为
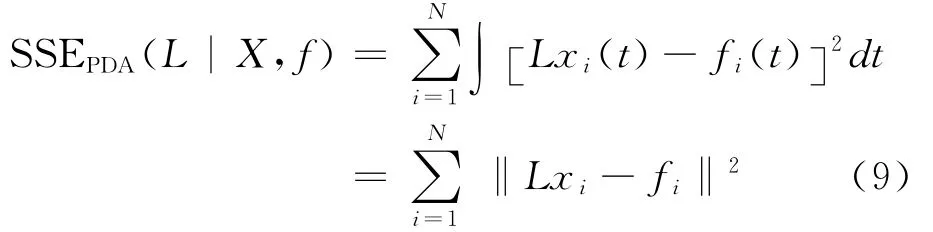

通过式(9),我们计算得到式(4)中系数βi,i=0,…,1…,m-1的大小,进而得出微分算子L,通过找到L所张成空间中m个正交的函数uj,j=1,…,m,可得到微分方程的解维中占比重最大的原始指标;主微分分析的经济意义更多地表现为研究对象自身的特性,需从研究对象的数据变化特征和实际指标变化的对比中发掘。主成分分析实质在于降维,而主微分分析不用考虑降问题,是处理高维问题的一种简洁方法。
其中,f是对应的扰动函数,u为微分方程的解,u(x)=∫f(t)G(x,t)dt,G(x,t)为 对 应 的 格 林 函数,更详细的介绍参见 Roach等人的研究[9]140-173。
由于所得微分方程的基础解uj,j=1,2,…,m正交,则对于满足此方程的任意x(t),均可以近似的表示为
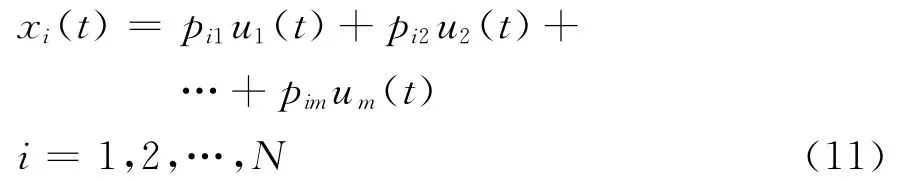
可以通过对 {pi1,pi2,…,pim}的对比分析挖掘不同时间序列数据的差异性。
综上所述,发现主微分分析与主成分分析的不同之处,主成分分析通过分析不同序列得出相互正交的新的综合指标。而主微分分析的关键在于引入微分算子,通过微分算子张成的子空间反应序列的特征。主成分分析的经济意义往往来自于综合指标
三、实证分析
(一)数据的函数性统计特征
本节利用函数型数据分析来研究中国2000—2010年的全国银行间同业拆借利率的发展变化趋势。在数据分析过程中,选择1个月、2个月、3个月、4个月共计4个种类的平均拆借利率为研究对象,共计120个月,其中15个数据缺失。依据常识,利率的变化具有周期波动性,所以在分析过程中采用Fourier基函数来做拟合。利用基于MATLAB的编程,通过对100个基函数拟合系数判断,根据计算结果,100个基函数刻画中只有前面15个左右的系数比较显著,后面的几乎接近于0,所以选取15个fourier基函数对原数据进行拟合,并绘出不同期限利率的修匀曲线及拟合残差平方和(RMS)。由图1可知,每一条曲线代表一个函数关系xi。根据拟合残差平方发现,修匀结果比较理想。
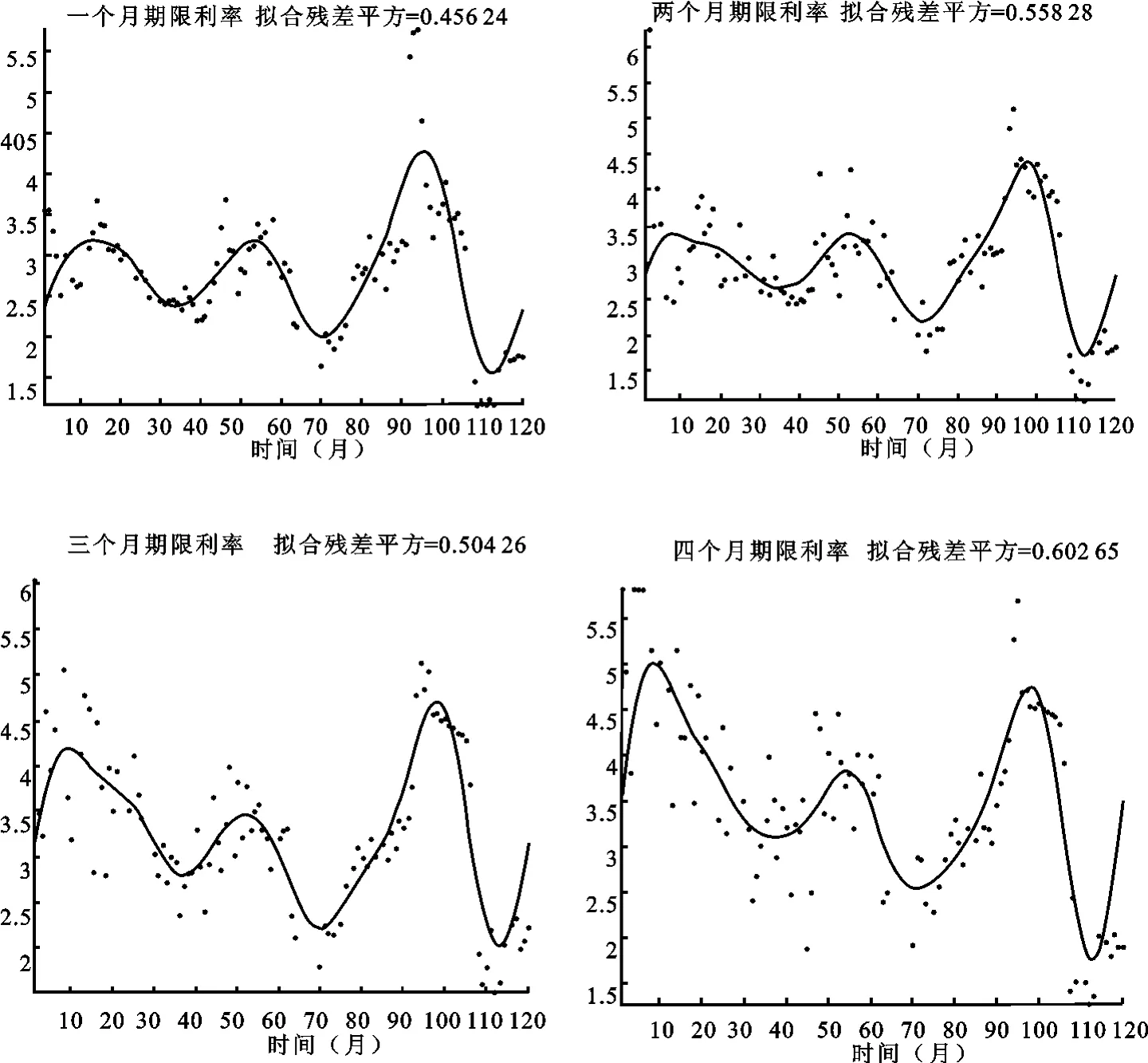
图1 利率的修匀曲线图
从函数的视角,对具有函数特征的统计数据进行研究,会挖掘出更多的信息。如上所述,通过对函数型数据修匀曲线的表示,不但能够诊断拟合数据的可能数学模型,还可对修匀曲线求一阶或高阶导数,来进一步探索数据的个体差异和动态变化规律。
图2表明不同期限利率的变化速度(一阶导数)曲线总体呈周期性变化的趋势,不同期限利率的变化速度基本相同,这与中国银行间同业拆借利率受法定利率的影响有关,二者具有较强的正相关性。进一步绘出利率变化率的波动情况,即不同期限利率变化加速度(二阶导数)曲线,结果见图3。可见不同期限的利率的波动情况差异不大,亦呈周期性特征,随着二阶导数波动幅度不断增大,拆借利率的变化能力不断增强。总体来说,不同期限利率的变动情况具有联动性、同步性。从利率变化速度曲线可以看出,2008—2009年利率增速减小并最终为负,而从利率变化加速度曲线分析,利率的变化速度较大。从图2及图3中还可以发现,利率的变化速度、加速度曲线与中国10年间经济走势是密切相关的。
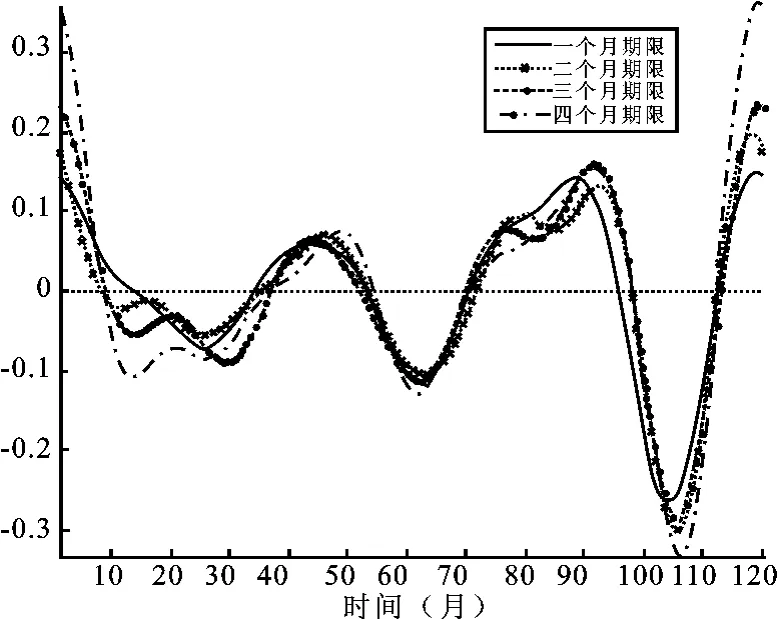
图2 不同期限利率变化速度曲线图
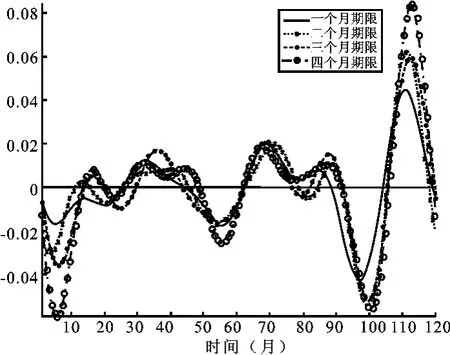
图3 不同期限利率变化加速度曲线图
在对函数型数据进行分析的过程中,为了进一步掌握函数型数据的的特征和规律,便于更深入的分析,与传统的统计分析一样,需要找到能够反映数据特征的代表值。
均值函数为:

方差函数为:
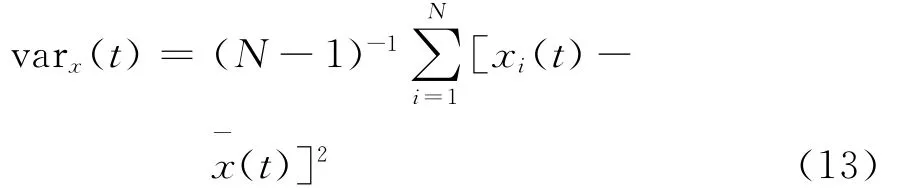
标准差函数是方差函数的平方根。其中,x1(t),x2(t),…xN(t)表示N个个体。
利用基于MATLAB编写的程序,绘出四类不同期限利率的均值函数和标准差函数曲线如图4所示。从图4中可以看出利率随着时间的变化形成较为规则的周期性变动,平均波动周期为36个月,而利率的标准差呈现波动性的递减趋势。说明利率水平逐渐的趋于平缓,金融市场趋于稳定,这也与中国金融市场不断完善,产品不断丰富,规模不断增长有密切关系。
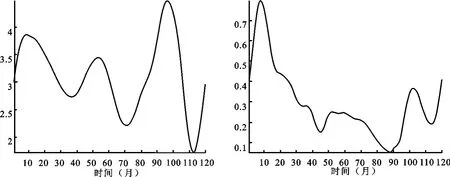
图4 均值函数和标准差函数曲线
为了分析不同期限拆借利率之间的动态变动关 系,进一步考察不同阶导数之间的相互关系,图5给出了二阶导数(曲率)相对于一阶导数(梯度)的关系图,即相平面分析方法。我们看到每一条曲线的周期变化数量一致,包含三个周期。在120个月中,三个圆形的周期正好对应了经济变化的周期趋势。后约50个月对应最大的圆环,前70个月中时间等分对应两个较小的圆环。2008年开始随着美国次贷危机的延伸,中国经济出现新一轮的下跌趋势,之后随着政府的经济刺激计划等措施的出台,经济又开始回暖。当然我们观察到随着时间演进,周期圆环不断增大,由于纵坐标表示的是同业拆借利率的曲率,而大的圆环正好表明经济体逐渐增强的变化能力(加速度)。就不同个体而言,较长期限利率对应较大的圆环,说明利率的波动幅度更大,变化能力也更为强劲。
(二)主微分分析结果
如前文所述,依据主微分分析的相关思想,我们利用基于MATLAB的编程对数据进行主微分分析。在此,通过对不同阶微分方程拟合结果对比,我们采用二阶微分方程进行分析,如下所示:

其中第一个参数β0主要反映x的位置因素,而β1则体现出整个系统的变化速度。通过编程运算得到权重函数的图像如图6所示。
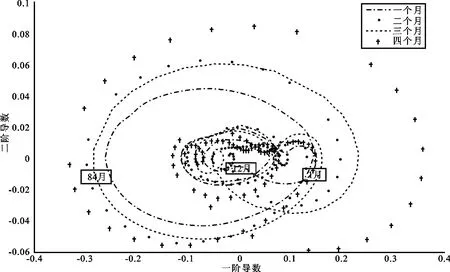
图5 一阶导数与二阶导数的相平面分析图

图6 权重函数的图像
可见,β0和β1均表现出强烈的波动性,而且都是以0为中心波动,β1的幅度较大。由β0和β1的值可以得出任意时刻不同期限的同业拆借利率所满足的微分方程,并由微分算子表达式可以直观的观测到利率位置和相应的梯度变化。
为了进一步探究主微分分析的结果,判定微分算子L在xi中的拟合效率,只需计算线性微分算子Lxi的大小,若只有很小的误差,就可以断定,主微分分析取得了比较满意的结果,由结果可知各函数对应的L均比较小(‖L‖<0.05)。另一方面,注意到不同期限利率对应的残差函数趋势基本不同,这表明除去微分方程提取的主成分因子外,残差函数表示不同期限利率相异的特征。为了进一步检验微分算子对原函数的拟合,表1列出了相关的回归统计量,发现残差平方和均小于3%,从经济意义上可知拟合结果显著,F检验的P值均在1%的水平下显著。所以,可以进一步断定,主微分分析取得了非常显著的结果。
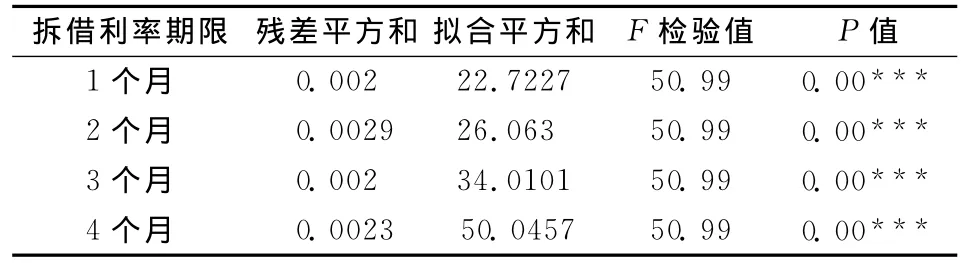
表1 主微分分析拟合结果统计量
接下来我们进一步针对拟合得出方程式(9)进行分析,由于采用微分方程进行了成分分析,拟合得出了微分方程相对应的系数,则可以通过求解微分方程来观察利率曲线在微分算子张成空间上的一些性质。如图7所示给出了初值分别为y0=6,Dy0=2和y0=2,Dy0=0的微分方程数值解。
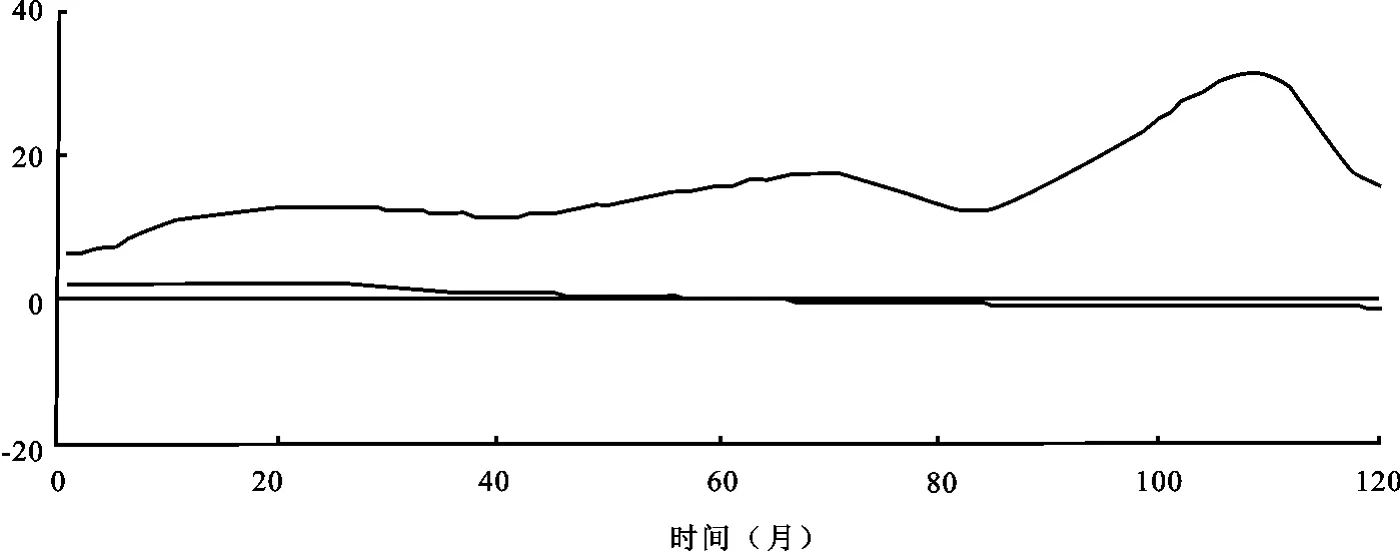
图7 微分方程数值解
根据微分方程的基础解系(包含如上所述两个基础解),我们可以求解得式(11)中每列利率数据的函数对象所对应的基础解系数,如表2所示。从系数p1
,p2可知,随着利率期限的增加,相对应的系数也有递增的趋势。这与利率期限结构理论所得结果一致,较长的期限对应较高的利率。由于数值解已给定,而且正的数值解占较大的优势,所以较长的期限对应较大的系数。

表2 微分方程基础解拟合利率曲线系数

图8 基于微分方程的拟合图
最后,为了进一步判断主微分分析的效果,图8给出微分方程解函数,利率数据曲线以及函数型数据拟合曲线的对比(以一个月期限利率为例,其余期限结果相似),从图8中信息可知,拟合效果比较理想,表明主微分分析方法具有可靠的实际应用价值。
四、结 论
在经济实践中,越来越多的领域所得到的样本观察资料是曲线或图像,即函数性数据。因此对这种类型的经济数据进行统计分析和描述具有重要的现实意义。研究着重介绍了函数型数据分析中主微分分析的特征及处理方法。从文中分析可知,函数型数据分析在处理数据缺失等不规则数据方面具有独特的优势。进一步分析发现,经济计量分析中的面板数据实则是函数型数据的一种特例,在此基础上可以为面板数据分析提供更多更好的工具。在函数型数据拟合中,本研究首次运用基函数系数的大小判断最优基函数的个数。通过对微分方程解函数及其系数的分析,进一步拓展了主微分分析方法的内容。另外,通过对全国银行间同业拆借利率进行分析,例证了主微分分析方法的优势。具体表现在:第一,较少的假定条件与较弱的结构约束,只需假定函数的光滑性;第二,不要求不同观测对象的观测点与观测次数相同;第三,通过对函数型数据不同阶微分曲线的分析,探索数据的动态变化特征等。对于主微分分析方法在处理高维甚至无限维数据中的优势,仍需深入研究。
当然,主微分分析这一方法研究尚处于起步阶段,有许多理论还需完善。本研究分析中,只是给出了微分方程数值解的拟合效果,在接下来的研究中,可以在样本外预测等方面做进一步探讨。这对于主微分分析方法在金融时间序列及面板数据分析中具有较为深远的意义。
[1] 严明义.函数型数据的统计分析:思想、方法和应用[J].统计研究,2007(2).
[2] 严明义.经济数据分析:一种基于数据的函数型视角的分析方法[J].当代经济科学,2007(1).
[3] 靳刘蕊.函数型数据分析方法及应用研究[D].厦门大学博士学位论文,2008.
[4] 叶振军,张庆翠,王春峰.时变参数N-S期限结构模型的主微分分析及其实证研究[J].预测,2009(4).
[5] Ramsay J O.Principal Differential Analysis:Data Reduction by Differential Operators [J].Journal of the Royal Statistical Society.Series B(Methodological),1996,58(3).
[6] Poyton A A,et al.Parameter Estimation in Continuous-time Dynamic Models Using Principal Differential Analysis[J].Computers & Chemical Engineering,2006,30(4).
[7] Ramsay J O,Ramsey J O.Functional Data Analysis of the Dynamics of the Monthly Index of Nondurable Goods Production[J].Journal of Econometrics,2002,107(1-2).
[8] Ramsay J O,Silverman B W.Functional Data Analysis[M].New York Springer,Inc.1997.
[9] Roach G F.Green′s Functions:Introductory Theory with Applications[M].VanNostrand Reinhold,New York.1970.

