递归预测器神经网络在中国金融市场的实证研究

黄腾飞，李帮义，熊季霞

（1．南京航空航天大学 经济管理学院，江苏 南京 210016；2．南京中医药大学 经贸管理学院，江苏 南京210046；）

一、引 言

近年来，作为市场经济体系的有机构成部分，全球金融市场的规模急剧扩大，其重要性日益凸显。作为一个新兴的市场，中国金融市场的发展更是举世瞩目。2009年，中国A股市场市值已跃居全球第二，2010年实现了真正意义上的全流通，形成主板、中小板、创业板、退市板（三板）四架马车并行的格局。如今，新三板又将推出。中国的期货市场经过20年的蓬勃发展，已成为全球第一大商品期货市场，交易品种覆盖了农产品、金属、能源、化工等诸多产业领域。国内首个金融期货品种——沪深300指数期货也在2010年上市。中国的黄金市场虽然起步较晚，2002年10月才正式交易，但经过近10年的发展，无论是交易量还是市场影响力都有了长足的进步。目前中国，金融投资已逐步成为个人、企业乃至政府的重要理财工具，金融时间序列预测也是金融理论领域的研究热点之一。

在传统的有效市场理论框架下，金融市场分析由线性范式主导。但是近年来，有关金融市场存在非线性和确定性的证据被不断发现。在证券市场，马超群等用BDS方法检验表明，中国股票市场具有混沌特征，可以用最少三个动态变量作为股票市场系统的运动建立模型［1］；谢朝花等用 R／S分析、相空间重构、主分量分析等方法肯定了上海股票市场的分形和混沌特征［2］。在期货市场，黄腾飞等系统地检验了中国期货市场的混沌性［3］。唐衍伟等利用R／S分析方法研究了中国农产品期货市场价格波动的长程相关性［4］。李锬等应用R／S分析方法研究了中国农产品期货市场的持久性趋势和非周期循环长度［5］。何凌云等用相空间重构方法分析了大连豆粕期货价格的混沌特性［6］。在黄金市场，黄腾飞等研究和比较了中外黄金市场的混沌特性［7］。现在一般认为，国内金融市场普遍存在弱混沌。

针对具有混沌动力学特性的国内金融市场，学者们已经建立了一些预测模型。其中神经网络模型预测精度高，方式灵活，在单步预测外还可以直接进行多步预测，受到广泛的重视。最近的实证研究成果有陈敏、马明等的BP神经网络模型［8－9］，张中华等的RBF神经网络模型［10－11］，牛国鹏等的小波神经网络模型［12］，杨新斌、向昌盛等的支持向量机模型［13－14］，以及王海军等的基于粒子群神经网络的期货价格预测模型等［15］。但是，前述这些神经网络模型都属于静态前馈的处理模式，内部没有包含延迟和反馈环节。而这些环节通常存储有对过去信息的记忆，这对于金融时间序列预测来说是不应忽视的。

递归预测器神经网络（Recurrent Predictor Neural Network（RPNN））是 Han等人在2004年提出的［16］，它是在通用学习网络（ULN）的基础上发展起来的一种特殊多重分支时间延迟递归神经网络。其节点代表过程状态，节点之间的分支及分支上的延迟代表状态之间的因果关系，这样依靠对输入输出样本的学习，自适应地提取样本中蕴含的动态规律。并且，其动态特性和存储能力可以较好地反映动力学系统的时序特性，从而有效提高预测精度。

本研究以金融市场普遍存在的弱混沌为基础，运用递归预测器神经网络对中国金融市场进行预测。在网络训练上，提出用遗传算法优化网络的阈值、权值以及激发函数的幅值和斜率。对国内股票、期货和黄金市场中几个有代表性的品种进行实证检验，计算了预测均方根误差（RMSE）和预测精度（PA），并和其他典型的神经网络预测方法——BP神经网络、径向基函数神经网络等做了比较，结果表明本研究的训练方法有较好的预测效果。

二、递归预测器神经网络模型

混沌时间序列预测就是对混沌信号的未知非线性映射函数进行逼近的过程。设xt为长度为n的混沌时间序列，构造嵌入维数m，时延为τ的嵌入向量X（t）＝ ｛xt，xt＋τ，…，xt＋2τ，…，xt＋（m－1）τ｝，则 由Takens嵌入定理知，相空间中必然存在函数Φ，使得延时τ后的状态X（t＋τ）和当前状态X（t）之间满足

其中Φ就是待逼近的非线性映射函数。所以神经网络预测实际上是利用神经网络的强逼近能力来逼近混沌时间序列的映射函数，据此从当前状态点计算出下一延时（一步预测）或多个延时（多步预测）后的状态点。

（一）神经网络结构

递归预测器神经网络（RPNN）是一种特殊的多重分支时间延迟递归神经网络，其特点是：1．网络不包含隐含层，网络结构完全由节点数和分支数决定。对于混沌时间序列预测，可取节点数＝分支数＝重构后向量维数（嵌入维数）；2．网络只具有局部反馈方式，各节点输出只反馈到自身以及后继节点；3．节点之间具有多重分支，分支的时间延迟也是不同的，体现了节点之间的联系。

RPNN的网络结构见图1所示。

由图1可见，RPNN各节点在每一个节拍的输出都会反馈到自身及其后的节点，形成附加的输入。这种递归使得RPNN具有某种内在的动态记忆属性。设hj（t）为节点j在时刻t的输出，Fj为节点j的激发函数，rj（t）为t时刻节点j的外部输入，θj为节点j的阈值，Dij（p）为节点i到节点j的第p条分支的时延，wijp（t）为节点i到j第p条分支在t时刻的权值，则网络输出方程为

神经元激发函数Fj一般取双曲正切函数

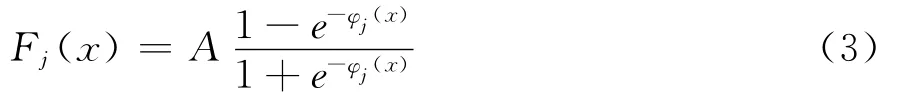
其中A为幅值参数，φ为斜率参数。

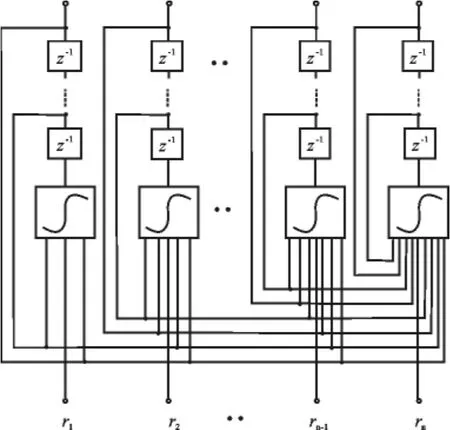
图1 递归预测器神经网络结构图

（二）结合时序偏微分和BPTT的训练算法

根据图1所示的网络结构，可以选定网络训练目标函数为

其中S为样本总数，M为输出维数，hj（t）为网络输出 ，j（t）为期望输出。

Han提出的训练算法是在传统的BPTT算法上结合时序偏微分［16］，其网络权值参数调整为：

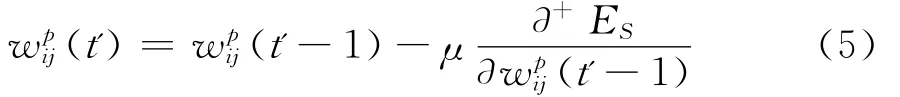
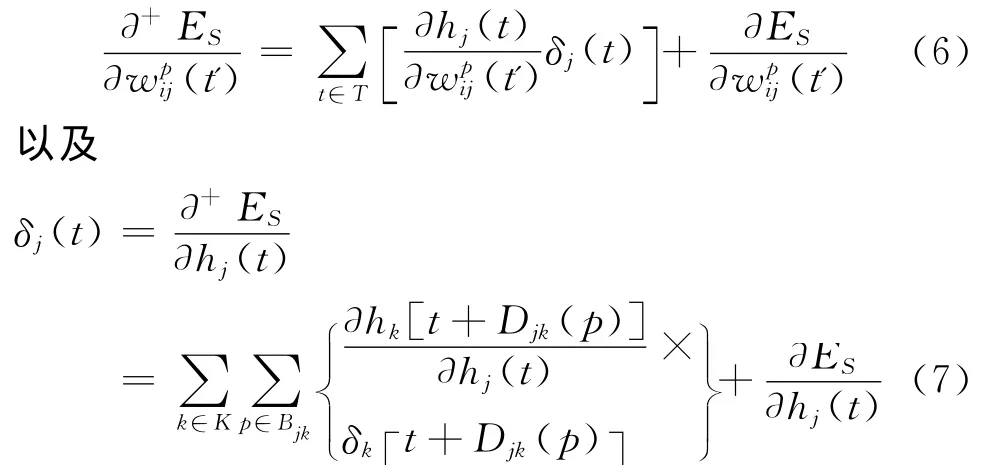
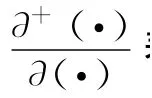
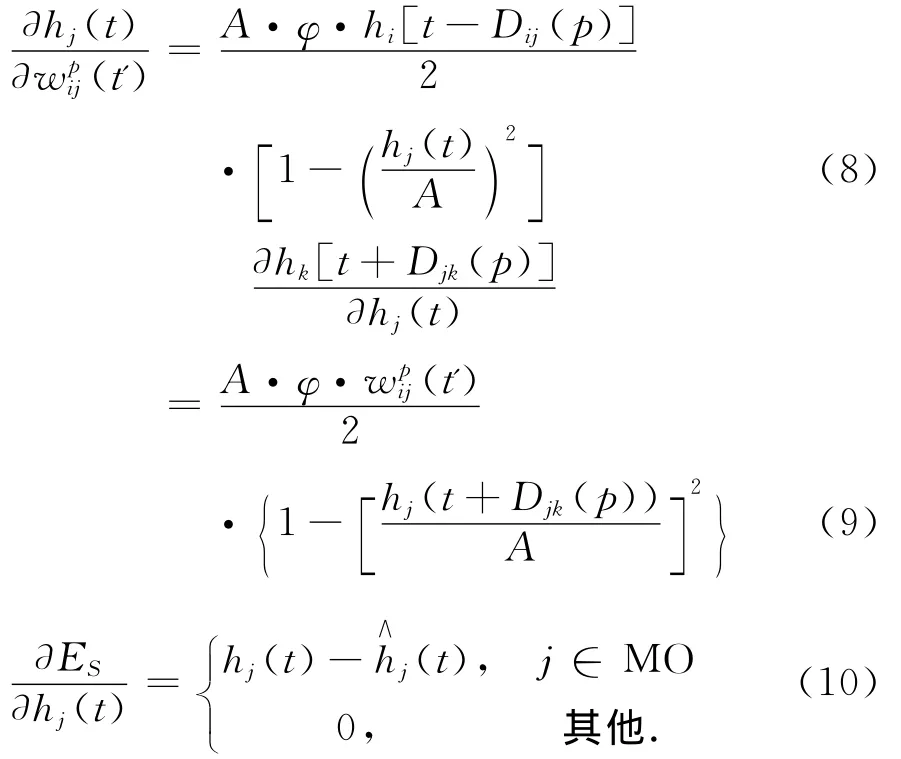
如此依照梯度下降原则调整权值，网络目标函数最终可以收敛。

在时序偏微分＋BPTT训练算法中，学习率参数μ对收敛速度影响很大。韩敏建议让学习率根据误差函数值及其梯度的变化进行自适应调整［17］86－87。设a0＞1，0＜a1＜1，a2＞1均为常数，则

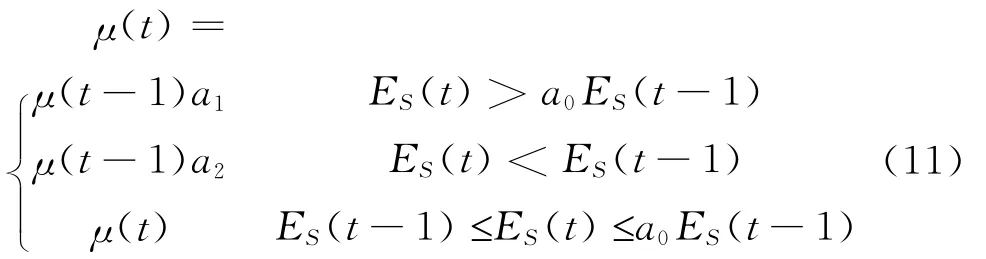
（三）遗传训练算法

前述的时序偏微分结合BPTT的训练算法较为复杂，并且也存在着可能收敛到局部极小值点的问题。而且算法的稳定性受学习率的选取影响很大。该算法只能对网络连接权值进行优化，不能优化各神经元的激发函数参数。遗传算法（Genetic Algorithm（GA））是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法，它采用群体搜索策略，群体中个体之间进行信息交换，在搜索时不依赖于梯度信息。优点是简单、通用，鲁棒性强，具有隐含的并行分布处理和强大的全局搜索能力，可以较好地解决上述问题。

1．染色体编码与设计

本研究对每个个体赋予两个染色体，均为实数编码。第一个染色体编入神经元激活函数信息，由A，φ两种基因组成，分别表示激活函数的幅值参数和各神经元激活函数的斜率参数；第二个染色体编入阈值与权值信息，由各神经元阈值θ和各分支的连接权值W两部分组成，见表1。

表1 染色体设计表

3．选择策略

采用赌轮选择策略（roulette－wheel selection）。个体xi被选中的概率Pi与其在群体中的相对适应度成正比，即

2．适应度函数构造

算法的目的是搜索最佳的激活函数参数和阈值、权值参数，使神经网络预测性能最佳。因此，可以取式（4）中网络误差函数ES的倒数作为适应度函数，即

其中n为染色体长度，g和h为基因。设m为区间［2，n－1］的随机整数（交叉点），则子代染色体为

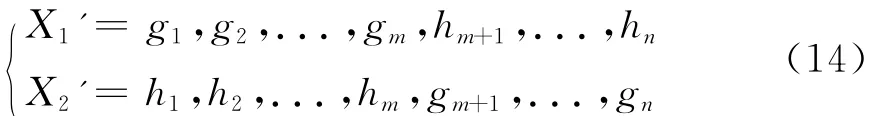
其中f（xi）为个体xi的适应度。

选择完毕后，再根据最佳保留策略，将当前群体中适应度最高的个体完整地复制到下一代群体中。

4．交叉策略

按交叉概率Pc进行染色体交叉。对于选中个体的两个染色体均采用单点交叉策略，随机选择交叉点后，两个体在点一侧完整交换基因。设X1，X2为父本染色体

5．变异策略

以变异概率Pm选择基因进行变异。对于选中的基因gi，随机变异为上下界中的某个实数，即

其中b为［0，1］间的随机数。

三、实证研究

本研究以国内股票、期货和黄金市场中三个有代表性的品种进行实例仿真，数据来源为Bloomberg和文华财经数据库。由于期货合约品种有到期日，为确保长期价格数据的代表性，本研究采用了黄腾飞等提出的最大交易量复权法进行数据采样［3］。各市场的数据都经过对数线性去趋势平稳化（Log－Linear De－trending（LLD））处理和归一化。训练、预测完毕后，再反归一化，然后计算预测性能指标。

（一）对上证指数的预测实证

在股票市场，取上证指数日收盘价格序列，时间从1999年3月12日到2011年7月29日，共3 000个数据。数据先经LLD平稳化处理，再归一化。选嵌入维数m＝3，嵌入延迟τ＝1进行相空间重构。神经网络结构及仿真条件见表2。

表2 预测上证指数的神经网络结构及仿真条件表

网络包括3个节点，节点间由3条分支连接，第三个节点为输出节点。网络输入为t日、t－1日、t－2日数据，输出为t＋n日数据预测值，其中n为预测步数（本研究中为天数）。神经元激发函数为式（3）的双曲正切Sigmoid函数。

具体的预测步骤分为两步，第一步是取前2 500个数据（区间为1999年3月12日至2009年7月10日）作为学习样本，对神经网络进行训练。采用本研究的遗传算法，种群规模控制在50，进化代数为1 000，各参数取值区间见表2。初始化种群，然后进行编码、计算适应度、选择、交叉、变异等操作，循环往复，直到达到进化代数，完成训练。第二步是预测，由于训练好的递归网络除了含有优化的权值、阈值与神经元激活函数参数外，还存储有过去序列的有用信息，所以可以直接从第2 501个数据开始（2009年7月13日）对后500个数据进行预测和对比。

图2展现了遗传算法训练过程中适应度的变化，图2中上方的曲线表示最佳个体适应度，中间的曲线是群体平均适应度，下方的曲线为适应度标准差。

图3是对上证指数进行一天预测后反归一化，然后反LLD平稳化处理的部分预测数据与真实价格数据的比较。由于重合度较高，为了清楚地看出预测与实际的差异，我们只选取了最后50个数据（2011年5月2日至7月29日）做图。

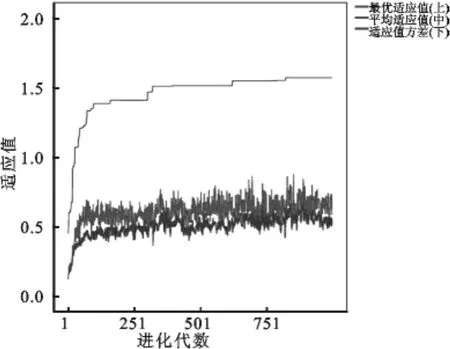
图2 RPNN遗传算法训练适应度变化图

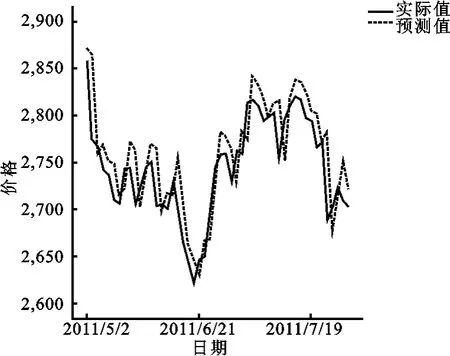
图3 上证指数一天预测结果图

为了比较预测性能，本研究对时序偏微分结合BPTT训练的RPNN（以下简称BPTT－RPNN），以及常用的BP神经网络、RBF神经网络等都进行了仿真预测，预测时域从1天到10天。

对于BPTT－RPNN，本研究固定神经元激活函数的幅值A＝1．0，斜率参数φ＝2．0，训练次数1 000次；对于BP神经网络，选择输入层节点数为m，隐藏层节点数为2m＋1，输出层节点数为1，采用Levenberg－Marquardt训练算法，训练次数1 000次；对于RBF神经网络，为保证良好的泛化性，我们逐步增加基神经元数量来尝试预测效果，经试算最佳径向基神经元数为10个。设定训练次数也为1 000次。

选择两种性能指标，即预测均方根误差RMSE和预测精度PA来定量地评价以上四种神经网络模型的预测效果。RMSE计算预测值对观察值的平均偏离程度，是反映预测性能的重要指标，其取值非负，值越小预测效果越好，预测无误差时等于零。PA则反映均值偏离相关性，取值范围［－1，1］，越接近1越好，预测无误差时为1。两个指标的定义为［18］：

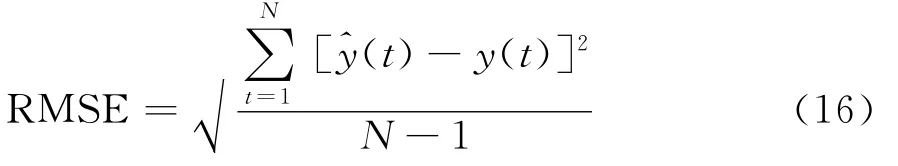
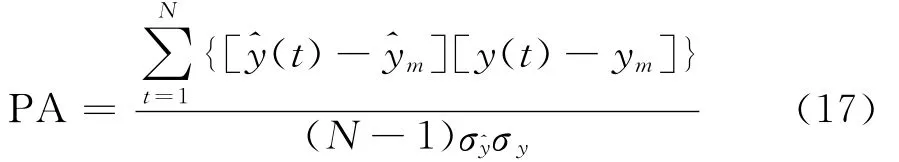
其中N为待比较样本数，y（t）和＾y（t）为预测值与期望值，ym、＾ym分别为其均值，σy∧，σy是它们的标准差。

在计算性能指标前，笔者已经对直接预测结果反归一化（但并没有反LLD处理）。预测的均方根误差和预测精度结果见表3和表4，表中BPTT指BPTT－RPNN，GA指GA－RPNN。为了让比较更直观，图4和图5绘出了这些模型的预测性能和。预测天数的关系

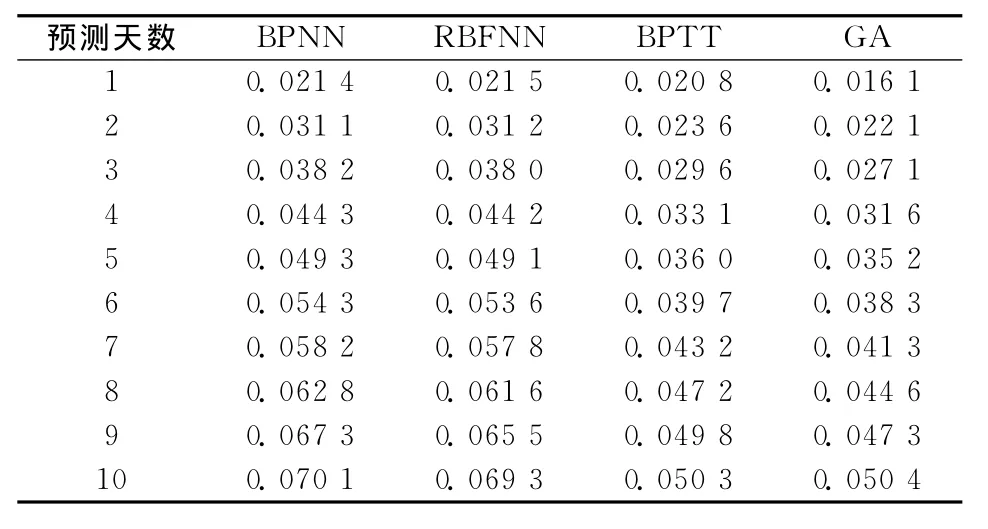
表3 上证指数预测均方根误差表

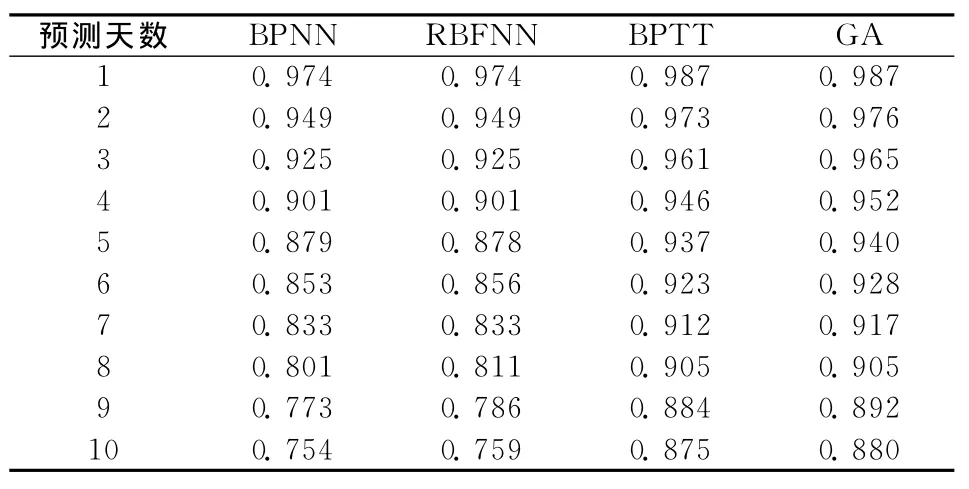
表4 上证指数预测精度表

可以看出，RPNN神经网络的预测效果要优于BP神经网络和RBF神经网络，而且随着预测时域的增加，这种优势更加明显。而本研究的GARPNN性能又要好于BPTT－RPNN。例如，对于一天预测的均方根误差值，GA－RPNN比BPTTRPNN要小20%以上。

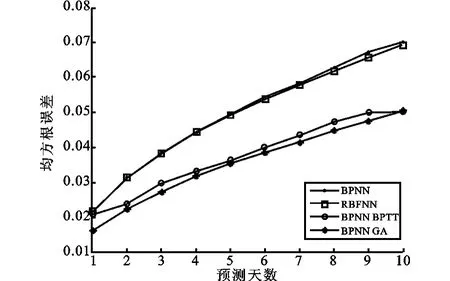
图4 上证指数预测均方根误差与预测天数关系比较图

图5 上证指数预测精度与预测天数关系比较图

（二）对期货市场的预测实证

本研究选择上海期货交易所天然胶期货合约来对期货市场进行预测实证。取2002年8月1日到2012年3月16日的日收盘价格，共2 336个数据。采样方法是最大交易量复权法，数据同样先经LLD平稳化处理，再归一化。选m＝5，τ＝1进行相空间重构，网络结构见表5，网络有5个节点，节点间5条分支，其他仿真条件同表2。

笔者用前2 000个数据（2002年8月1日至2010年11月1日）作为学习样本对网络进行训练，后336个数据（2010年11月2日以后）作为预测比较样本，遗传训练算法的步骤细节同上证指数，预测结果见图6所示，依然是取最后50个数据（2011年12月29日至2012年3月16日）做图。

表5 预测上海天然胶期货的神经网络结构表

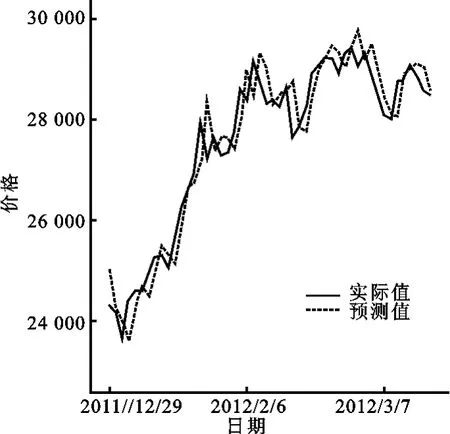
图6 上海天然胶期货一天预测结果图

为了比较预测性能，笔者也用基于时序偏微分＋BPTT算法的RPNN、BP神经网络和RBF神经网络对天然胶期货进行了1至10天的预测仿真。上述神经网络的参数选取同上证指数，预测均方根误差和预测精度见表6和表7，直观的预测性能比较见图7和图8。可见BPTT－RPNN依然优于两种常用网络，而GA－RPNN是最优的。

表6 上海天然胶期货预测均方根误差

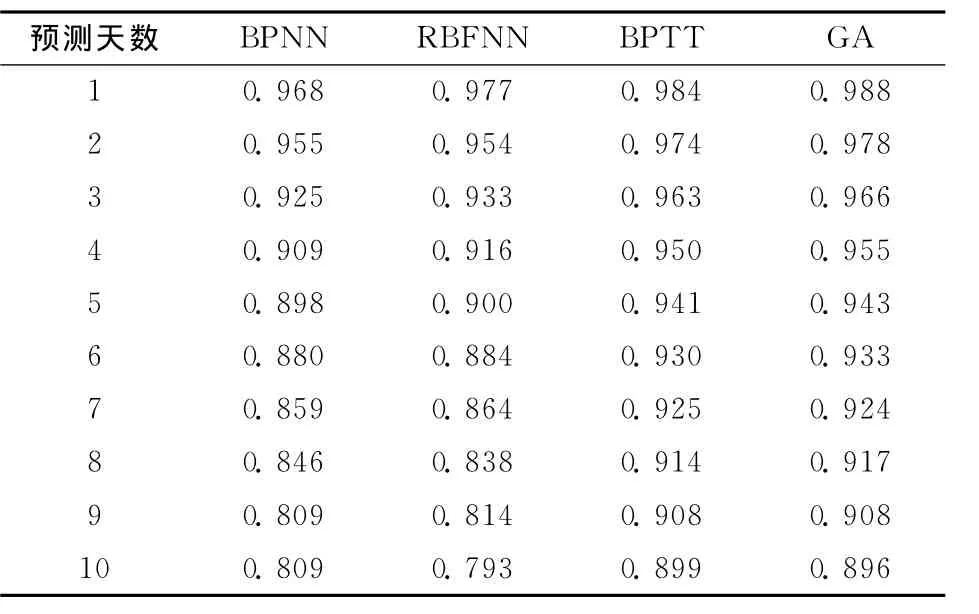
表7 上海天然胶期货预测精度表

（三）对黄金市场的预测实证

对于国内黄金市场，本研究选取的是上海黄金交易所纯度为99．95%的黄金现货交易日收盘价格，时间从2002年10月30日到2012年3月16日，共2 270个数据，数据的平稳化和归一化处理同上证指数。取m＝3，τ＝1进行相空间重构，由于所选嵌入维数同上证指数一样，因此神经网络结构和仿真条件与表2相同。

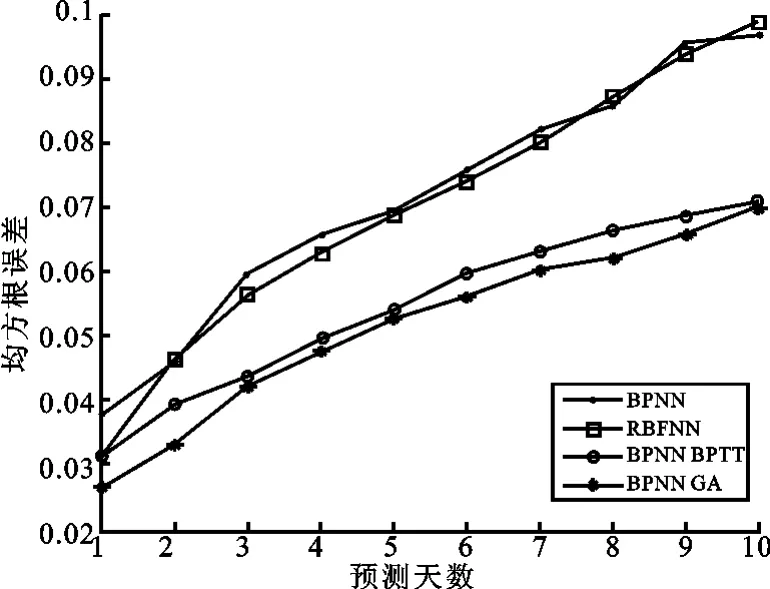
图7 上海天然胶期货预测均方根误差与预测天数关系比较图

笔者以前2 000个数据（2002年10月30日至2010年12月27日）作为训练学习样本，后270个数据（2010年12月28日以后）作为预测比较样本，训练算法步骤同上，一天预测的结果见图9。

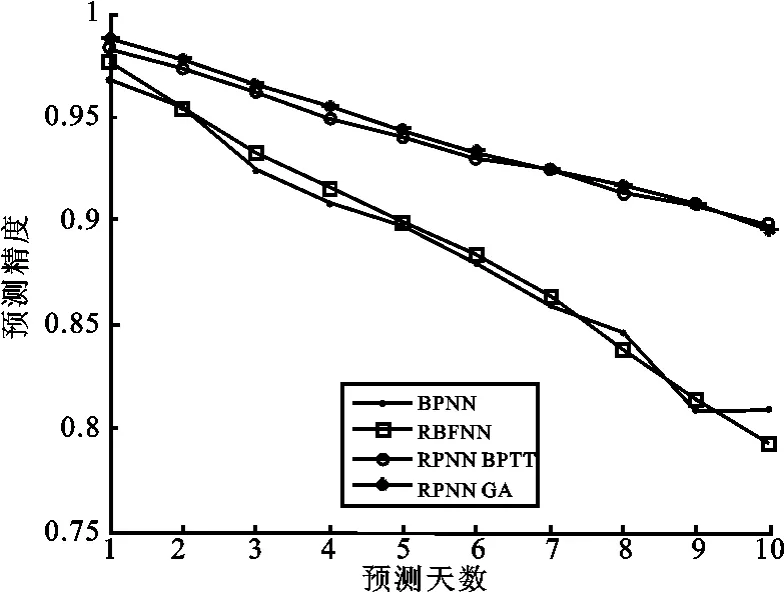
图8 上海天然胶期货预测精度与预测天数关系比较图

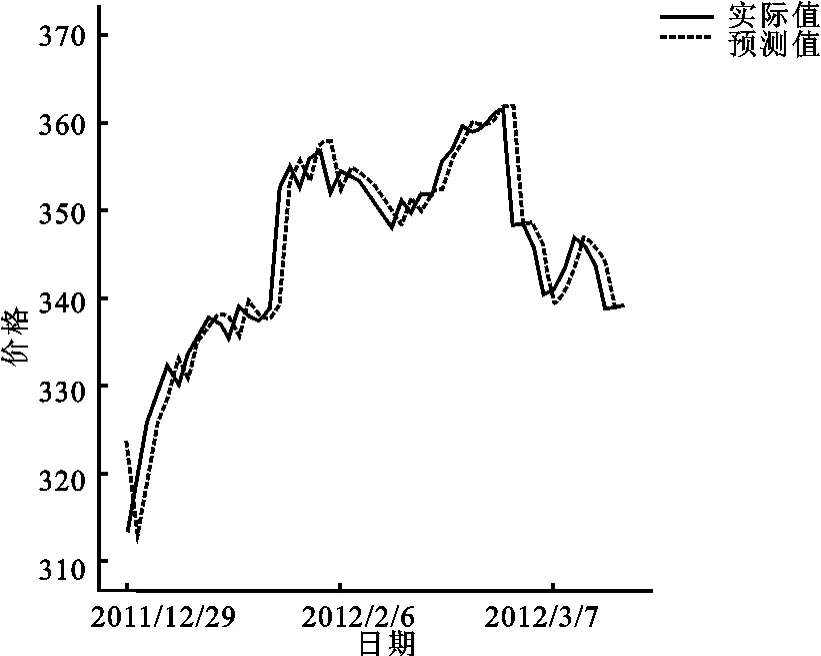
图9 上海黄金一天预测结果图

用其他三种神经网络模型上海黄金价格进行1至10天的预测仿真，所得预测均方根误差和预测精度数据见表8和表9，性能指标比较见图10和图11，从中可以得出和之前相似的结论。

表8 上海黄金预测均方根误差

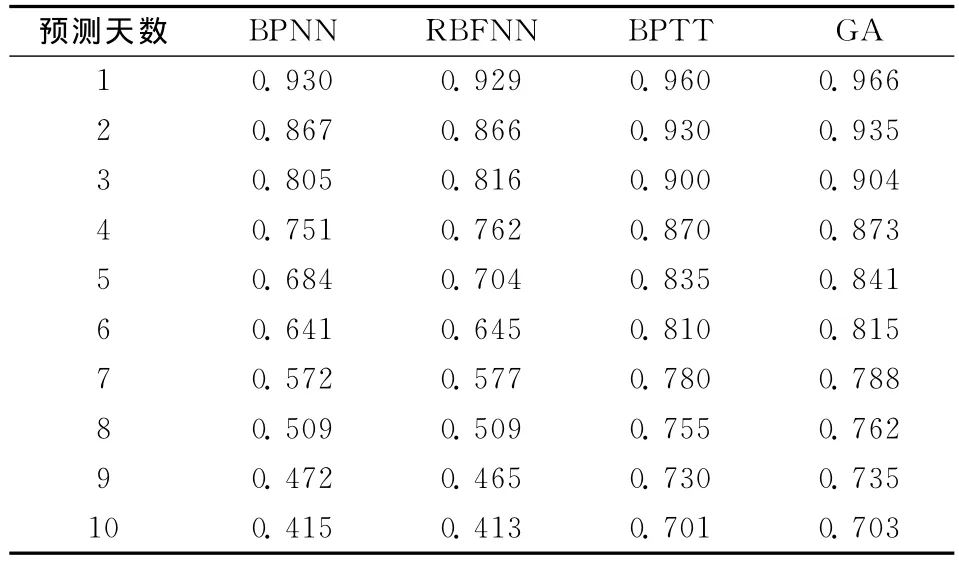
表9 上海黄金预测精度表

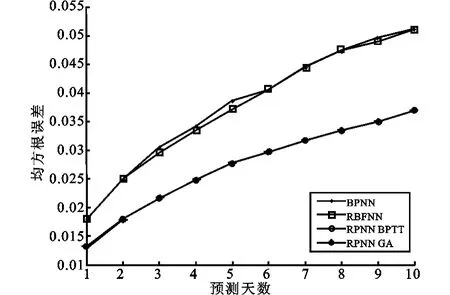
图10 上海黄金预测均方根误差与预测天数关系比较图

图11 上海黄金预测精度与预测天数关系比较图

四、结 论

本研究以金融市场普遍存在的弱混沌为基础，以递归预测器神经网络对中国的金融市场进行预测。在网络训练上，提出用遗传算法优化网络的阈值、权值以及激发函数的幅值和斜率。对国内股票、期货和黄金市场中几个有代表性的品种进行实证检验，计算了预测均方根误差（RMSE）和预测精度（PA），并和其他典型的神经网络预测方法——BP神经网络、径向基函数神经网络等做了比较。通过这些实证研究，可以得出如下结论：1．递归预测器神经网络由于其动态性和对历史信息的存储能力，适合对金融市场的预测，相比于常用的BP神经网络和RBF神经网络，在预测性能上有明显优势；2．采用遗传算法来训练递归预测器神经网络，克服了经典的BPTT训练算法的算法复杂及可能收敛到局部极小值点等缺点，在预测性能上也有提高。3．本研究的遗传训练算法虽然能得到较高的预测精度，但作为一个通用算法，耗费计算机的机时较多。今后可以考虑把遗传算法同BPTT算法结合起来，以提高网络训练效率。

［1］ 马超群，邹琳，李红权．股票市场的非线性结构与混沌效应检验——基于BDS与CR方法［J］．湖南大学学报：自然科学版，2008，35（5）．

［2］ 谢朝花，李 忠，郑咏梅，文凤华．中国股票市场分形与混沌特征：1994～2008［J］．系统工程，2010，28（6）．

［3］ 黄腾飞，李帮义，熊季霞．中国期货市场的混沌性检验［J］．系统工程，2012，30（1）．

［4］ 唐衍伟，陈刚，张晨宏．中国农产品期货市场价格波动的长程相关性研究［J］．系统工程，2005，23（12）．

［5］ 李锬，李鹏，齐中英．农产品期货价格时间序列 R／S分析［J］．商业研究，2006（5）．

［6］ 何凌云，周曙东，徐才华．基于PSRT的大连豆粕期货价格的混沌判据［J］．系统工程，2008，26（6）．

［7］ 黄腾飞，李帮义，熊季霞．中外黄金市场混沌特性比较－－基于相空间重构技术［J］．技术经济，2012，31（10）．

［8］ 陈敏，叶晓舟．混沌理论在股票价格预测中的应用［J］．系统仿真技术，2008，4（4）．

［9］ 马明，李松．基于遗传算法优化混沌神经网络的股票指数预测［J］．商业研究，2011（11）．

［10］ 张中华，丁华福．基于混沌神经网络的股票分析及其预测［J］．计算机技术与发展，2009，19（3）．

［11］ 任亚，李萍．基于RBF神经网络的中国CPI预测研究［J］．西安财经学院学报，2011，24（1）．

［12］ 牛国鹏．小波网络与混沌时间序列预测［D］．兰州大学博士论文集，2009．

［13］ 杨新斌，黄晓娟．基于支持向量机的股票价格预测研究［J］．计算机仿真，2010，27（9）．

［14］ 向昌盛，周子英，余喜林，张林峰．遗传算法在混沌时间序列预测中的应用研究［J］．计算机应用研究，2011，20（8）．

［15］ 王海军，白玫，贾兆立．基于粒子群神经网络的期货价格预测［J］．计算机工程与设计，2009，30（10）．

［16］ Han M，Xi J，Xu S，Yin F L．Prediction of Chaotic Time Series Based on the Recurrent Predictor Neural Network［J］．IEEE Transactions on Signal Processing，2004，52（12）．

［17］ 韩敏．混沌时间序列预测理论与方法［J］．北京：中国水利水电出版社，2007．

［18］ Chen J L，Islam S，Biswas P．Nonlinear Dynamics of Hourly Ozone Concentrations：Nonparametric Short Term prediction［J］．Atomospheric Environment，1998，32（11）．