基于广义双曲线SV模型的极值风险度量研究
周孝华,姬新龙,马 宁
(重庆大学 经济与工商管理学院,重庆 400030)
一、引 言
在险价值(VaR)自被引入风险管理领域以来,因其直观、易理解的特点,已经成为一种标准的风险管理工具,被金融机构和监管当局广泛采用。而选择合适的金融资产收益率分布,关系到VaR模型的有效性和合理性,已经成为学者们研究的热门问题。
传统的计量VaR方法都是以正态分布为基础,而现实的金融数据经常表现为尖峰、厚尾和不对称性,这就为VaR计算带来较大的误差。学者们对该问题展开了大量研究,相继提出用t分布、混合正态分布、一般误差分布、g-h分布等拟合收益序列,然而这些分布的使用条件都有一定的局限性。Barndorff-Nielsen提出了广义双曲线分布[1]。它是一种半厚尾的分布,并且具有良好的统计特性,常见的正态分布、t分布和gamma分布等都是它的极限形式。广义双曲线分布具有5个参数,根据参数的不同衍生出一些子类,如双曲线分布和正态逆高斯分布等,共同构成了一个非常灵活的分布族,可以更好地拟合金融收益分布的尖峰、厚尾和偏斜等特征。由于广义双曲线分布具有良好的统计特性,使其在金融领域中得到了广泛应用,一些学者提出了广义双曲线学生偏t分布,并取得不错的研究效果。
另一方面,当前学者们讨论最广泛的就是在GARCH模型的框架下,标准化残差的分布函数设定取得VaR的值。GARCH类模型在面对金融时间序列高峰厚尾、杠杆效应等显著特征时对VaR的测度亦显得脆弱[2]。而SV类模型对金融时序的刻画能力具有比GARCH类模型更大的优势,对金融市场波动特征的拟合效果更好[3]。另外,由于VaR方法是对正常市场交易情况下风险的度量,而极端市场情况下VaR的计量已经引起了学者们的注意。近年来,许多研究风险度量的学者纷纷利用极值理论(EVT)进行VaR估计[4]。极值理论不考虑序列的整体分布情况,只关心序列的极值分布情况,在极端条件下,用极值理论方法得到的VaR估计值与经验分布非常接近,提供了超越样本的预测能力,比常用方法具有更大的优越性[5]。目前,国内用极值理论对金融资产的风险测度大多集中于资产收益的正态分布、GARCH模型等方面,少量涉及到SV类模型,应用广义双曲线学生偏t分布的SV模型与极值理论相结合的还没有[6]。
SV-GHSKt模型是基于广义双曲线学生偏t分布(GHSKt)的SV类模型,能充分反映资产收益的非对称厚尾性及杠杆效应等特征。本文的创新表现在:从动态角度考虑VaR时间序列的特征,首次把广义双曲线学生偏t分布(GHSKt)引入随机波动模型,通过构建SV-GHSKt模型拟合资产收益的非对称厚尾性及杠杆效应等特征,然后与极值理论相结合拟合金融资产收益的尾部特征,进而组建新的风险度量模型!!基于SV-GHSKt-POT的动态VaR模型,最后对模型的有效性进行检验。
二、SV-GHSKt模型及参数估计

(一)模型构建
为了刻画金融时间序列的尖峰厚尾性,Taylor提出了基本的SV模型,SV模型与金融理论中资产定价的扩散过程直接相关,其特点是在它的方差表达式中引入了随机过程,因而被认为是刻画金融资产波动性最理想的模型之一。在基本的SV模型基础上,Yu提出了带有杠杆效应的SV模型如下[7]:
其中εt和ηt是误差项,ρ为相关系数,两个误差项的关系满足:corr(εt,ηt)=ρ。当ρ为零时,即为基本SV模型,当ρ<0时表示存在杠杠效应;yt是在t日的收益,也是鞅差分过程;ht表示t日的对数波动;φ为持续性参数,反映了当前波动对未来波动的影响,对于φ<1,SV模型是协方差平稳的。
为了把杠杆效应和非对称厚尾性都在模型中表现出来,我们这里借鉴Nakajima的研究成果[8],用广义双曲线学生偏t分布的变量ωt取代正态变量εt,具体形式如下:

其中IG表示逆则伽马分布,ν表示分布的自由度,(β,ν)值的大小直接影响金融收益序列的尖峰厚尾性。把式(2)带入式(1)得到具体的SV-GHSKt模型:

(二)参数估计
为了估计SV-GHSKt模型的参数,首先应得到模型的似然函数。设模型的待估参数为θ=(φ,σ,μ,ρ,β,ν),然后由全概率公式得到收益率序列yt在给定参数θ下的密度函数:
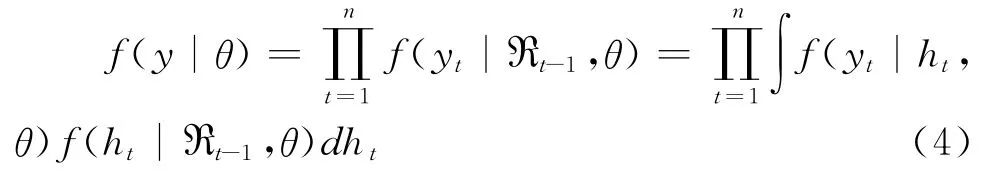

其中犚t-1表示收益序列在t-1时间的历史信息。从式(4)可以看出,基于广义双曲线分布的SV模型的密度函数形式复杂,参数估计非常困难,对其进行极大似然估计是一个高度非线性、具有大量局部最优陷阱的优化问题。这样常规的参数估计方法就遇到了困难,但利用计算机仿真的方法估计模型SV-GHSKt的参数,具体做法就是采用基于 MCMC的贝叶斯推断,根据极大似然估计思想,在遗传算法中引入模拟退火算法,来最大化基于广义双曲线分布SV模型的对数似然函数,以求得其参数。收敛性检验表明,该算法是稳定和可靠的[9]。采用Kim等的经验[10],选取以下分布作为先验分布:
三、基于SV-GHSKt-POT的动态VaR模型
(一)动态VaR模型
设pt是t时刻的金融资产价格,则其在t时刻的对数收益yt=lnpt-lnpt-1,令该收益序列的密度函数为f(y),则置信水平1-α下的VaR表示如下:

当采用了动态模型时,资产回报的波动具有异方差性,不适宜直接由分布计算其VaR值,而是将资产收益yt转化为标准残差Zt,便可通过Zt的VaR值预测yt的VaR值,进而得到置信水平1-α下,资产收益yt动态VaR的计算公式:

其中μ为期望收益,σt表示第t天的波动预测,VaR(Z)α表示残差项Zt在分位数为α时的风险价值。
(二)构造标准残差序列
极值理论中常用的是POT模型,由于资产收益的波动是时变的且可能存在一定程度的相关性,不宜直接采用POT方法拟合尾部分布,因此根据Mcneil和Frey等的研究成果,虽然金融市场的收益或损失序列不满足独立同分布特征,但其标准残差序列却能近似满足这一特征[11]。当采用动态模型时,资产回报的波动具有异方差性,不适宜直接由分布计算其VaR值。因此,考虑对标准残差项zt做尾部拟合,需要将资产收益yt转化为标准残差Zt。根据MCMC方法估计出的参数值,计算出收益序列的条件均值t和条件方差,则标准残差序列为:
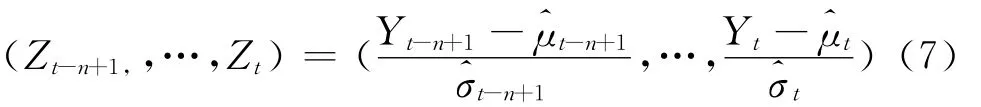
(三)基于SV-GHSKt-POT的动态VaR模型
接下来运用极值理论的POT模型拟合标准残差序列的尾部分布,这里定义u为阀值,γ为超阀值数据,依据PBH定理[12],可进一步将GPD分布函数引入式(8),则γ的累积分布函数可近似表示为:

其中β为尺度参数,ξ∈R为形状参数。当ξ≥0时,y≥0;ξ<0时,0≤γ≤β/ξ。ξ的不同取值决定了分布的厚度,ξ越大尾部越厚,ξ越小尾部越薄。为了估计POT模型的参数,首要的是选择合理的阀值参数u,然后用极大似然估计法估计参数ξ和β。在取得阀值之后,对POT模型进行极大似然估计,则得到标准残差序列的厚尾分布为:

为了处理方便,阀值的累积分布函数由(N-n)/N近似替代,N表示样本总数,而n表示高于阀值的标准残差数,则置信水平为1-α时的标准残差序列分位数为:
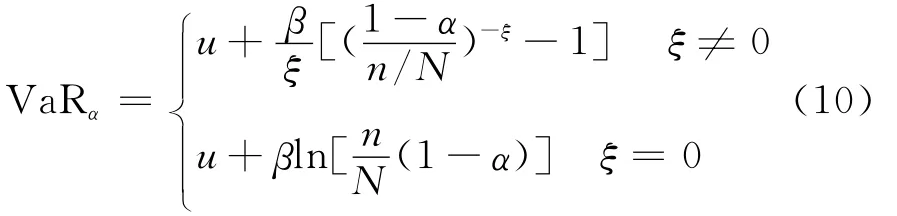
把式(10)带入式(6)得到在给定的置信水平1-α下,基于SV-GHSKt-POT模型的动态VaR为:

四、实证研究
(一)样本选取及统计特征描述
本文以上证综合指数(以下简称SSEC)每日收盘价为研究对象,考虑到我国证券市场涨停板制度给股票交易初始期带来的噪声交易影响,我们选取1996年12月26日至2012年3月5日为样本考察期,共3 673个样本,数据来源于雅虎财经网站。而为了样本数据的平稳性和精确性,采用对数收益率的100倍,即Xt=100*ln(pt/pt-1),pt为t时刻的指数的日收盘价。
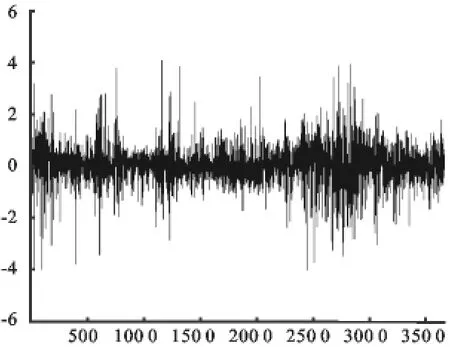
图1 SSEC收益序列图

图2 SSEC指数条件收益QQ图

表1 上证综合指数收益率的统计特征
图1、图2和表1给出了上证综合指数收益序列的描述性统计,图2是SSEC指数条件收益率的QQ图。从中可以直观地看出,SSEC条件收益率具有有偏性。从表1中可以看出,上证综指收益均值均接近于0,偏度都为负,峰度大于3,这说明上证综指收益率左偏且具有明显的尖峰厚尾特征;J-B正态性检验也说明收益率显著异于正态分布。从图1可以看出,上证综指具有典型的尖峰厚尾特点,且呈现非对称的分布,还有就是收益率的序列呈现一定的集聚性和爆发性。
(二)模型参数估计及检验
1.参数估计及收敛性诊断。首先对SVGHSKt模型的参数做贝叶斯估计,MCMC的Gibbs的抽样次数为50 000次,由于 Markov链收敛前的一段时间的迭代中,各状态的边际分布还不能认为是平稳的,因而选择“燃烧”舍去前25 000个抽样值,用后25 000次的抽样作为各参数的稳定分布抽样,参数估计结果如表2所示。

表2 SV-GHSKt模型的估计结果
从表2可以看到,ρ小于零表明序列存在杠杆效应,φ接近1体现了序列的波动集聚性,υ的估计值为14.524 0以及β不等于0表明上证综合指数收益率具有不对称厚尾性,因此,总的来说,SV-GHSKt模型对上证综指收益率序列的拟合效果还是可以的。而采用 MCMC估计,参数估计值序列的收敛性诊断异常重要,如果一个参数估计值序列不收敛,那就意味着它不会围绕一个值来波动,方差将会很大,也就是等价于一个回归模型中的回归参数的t值非常小,从而无法通过统计检验。基于此,我们要对SV-GHSKt模型进行收敛性诊断。
由表2可以看到,各个参数的MC误差远小于标准差,由此可以得到一个初步的结论,参数的估计趋于收敛。为了进一步证实这个判断,我们这里采用更为精确的方法G-R(Gelman-Rubin)收敛性诊断方法[13]16-17。Gelman-Rubin诊断方法以正态理论逼近为基础,最终得到一个判断收敛性的诊断统计量R,一般来说,>1,当 Markov链趋于收敛时应趋近于1。表2已经给出了G-R检验统计量,可以看出各个变量的G-R检验统计量均在1.0~1.1之间,因此,可以认为模型各个参数的样本分布已经收敛到其后验分布,即采用MCMC稳态模拟估计模型参数是有效的。
2.标准残差序列的EVT建模及检验。接下来做标准残差序列的POT参数估计。把上文的参数估计结果代入式(7)得到标准残差序列Zt,对标准残差序列进行检验,发现标准残差序列是独立的、稳定的,不存在自相关性,由此说明POT方法应用于Zt的VaR计算是合适的。在对标准残差进行POT建模之前,先要确定阀值u。通常估计阀值u的方法有3种:超额平均函数法、将阀值设定为标准残差序列的90%分位数和峰度法。考虑到阀值的选取对参数估计精确度的影响,先选择峰度法,然后再与超额平均函数法对比(考虑到篇幅,我们仅列举下尾的平均超额函数图见图3),进而确定阀值,最后通过极大似然估计法得标准残差尾部GPD分布的参数值,参数估计的结果如表3。
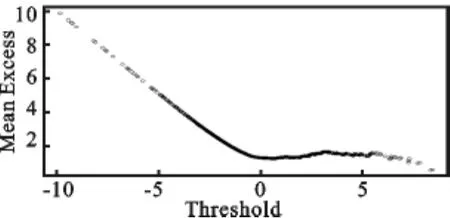
图3 标准残差下尾平均超额函数图
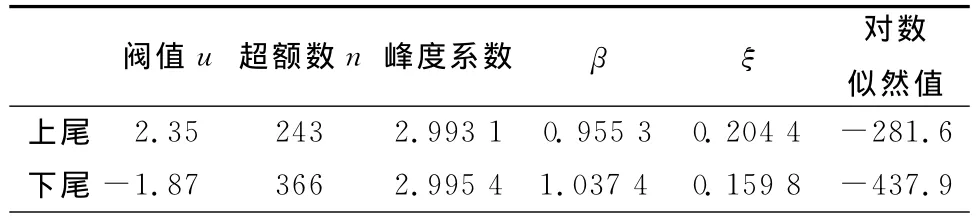
表3 上证综指标准残差序列的POT参数估计
应用POT模型做参数估计是否合理,需要对参数估计结果做检验。图4给出了标准残差Zt下尾分布拟合结果诊断的超额分布图、尾部分布图、残差散点图和残差QQ图。从超额分布图和尾部分布图可以看出,除个别点外,整体拟合的效果较好;从残差散点图和残差QQ图可以看出,拟合曲线均穿过散点密集区,散点紧密围绕直线分布,表明POT模型拟合尾部极值状态较好。因此,这里认为模型的选取是合适的,参数的估计是较为精确的。
为了进一步检验POT拟合方法的有效性,这里采用Choulakian等提出的拟合优度检验[14]。基本原理为:根据POT模拟方法估计的参数,计算Cramer-von统计量W2和 Anderson-Darling统计量A2,进而求出相应的P值,当W2和A2对应的P值都大于0.1的时候,说明尾部数据对应的阀值选取是合理的,POT方法对尾部的拟合是有效的,模型的选取是合适的。依据我们上面估计的参数,计算拟合优度检验相应的统计量(见表4)。

表4 POT方法的拟合优度检验统计量
由表4可见,上证综合指数的拟合优度两个统计量相对应的P值都大于0.1,根据Choulakian等提出尾部数据的选取标准,说明POT模型对尾部数据的拟合是合理的。因此,总的来说,阀值的选取是合适的,用POT模型拟合尾部数据是可行的,基于POT方法对SV模型做VaR分析是合理的。

图4 标准残差下尾分布的拟合效果图
(三)模型风险值的度量及效果检验
1.上证综指极值风险度量。基于前述分析,依据极大似然法估计出参数,为了比较分析方便,我们用POT模型拟合收益率序列的VaR和标准残差序列的VaR。
从表5分析可以看出,直接由SSEC收益率拟合的风险值显著高于基于标准残差序列的对应值,这说明在收益率序列不是独立同分布的情况下,直接应用GPD对超阈值进行拟合低估了真实的市场风险,同时也说明基于收益率序列得到的风险值更为保守。因此,可考虑采用独立同分布的标准残差序列来计算SV-GHSKt-POT的尾部风险值,然后将得到的静态POT模型下的尾部风险值代入公式(11),则相应得到在SV-GHSKt-POT模型下的动态VaR。接下来对SV-GHSKt-POT模型有效性做进一步分析。
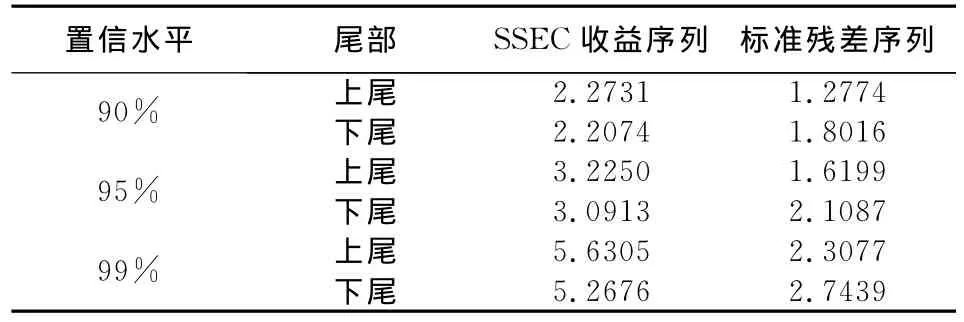
表5 不同置信水平下SSEC的VaR
2.SV-GHSKt-POT模型效果检验。为了检验模型的VaR预测精度,采用Kupiec的失败频率检验法来进行准确性检验。它的基本思想是,如果VaR模型计算值是准确的,那么实际损失超过VaR值的例外情况可视为一个二项分布中的独立事件,一个成功事件记为1,反之一个失败的事件记为0。Kupiec给出了这种检验方法的置信域,在置信域内失败次数越低,模型的预测效果越好,但失败次数过低,却意味着模型过于保守。依次选择置信度为0.90、0.95、0.99,分别用基于 SV-GHSKt-POT的动态VaR模型与基于SV-t-POT的VaR模型与POT的静态VaR模型预测上证综指数据样本的VaR值,然后与实际VaR值对比做后验测试,检验结果见表6。
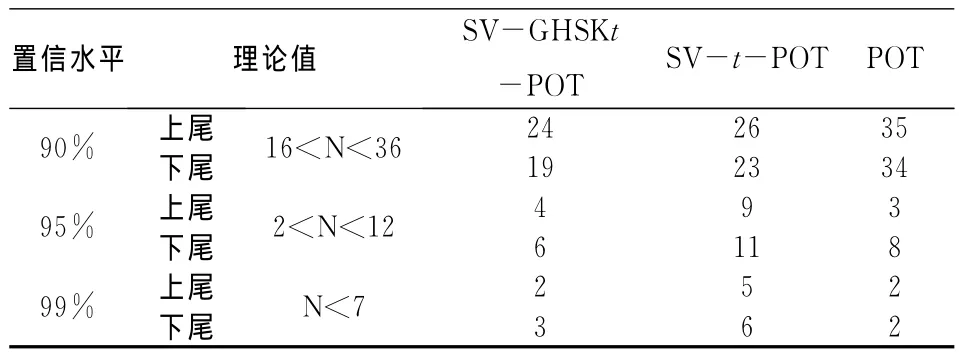
表6 VaR失败率的Kupiec检验结果(T=250)
由表6看出,置信度越高,各模型通过检验的失败次数越少,其中SV-GHSKt-POT模型和POT模型的表现更好;在相同的置信度下,基于SVGHSKt-POT的动态VaR模型相比SV-t-POT的VaR模型具有更少的失败次数,对VaR的预测效果更好。同时,根据Kupiec检验法,尽管基于POT的静态VaR模型具有更少的失败次数,但由于失败次数太少而造成了对VaR的估计过于保守,从而使风险高估。显然,基于SV-GHSKt-POT的动态VaR测度模型对上证综指的风险度量更加合理而准确。
五、结 论
本文应用EVT理论与SV-GHSKt模型结合建立基于SV-GHSKt-POT的动态VaR测度模型,并实证分析了上证综指的极值风险。研究表明,该模型能有效刻画股票市场的波动性特征,对市场风险的预测能力较强。同时,后验测试表明,基于SV-GHSKt-POT的动态VaR模型比以往的SV-t-POT的VaR模型更有效,比基于POT的静态VaR模型更具合理性,并且在高的置信水平下表现更好。
在对金融市场的尖峰厚尾、杠杆效应等特征的刻画方面,SV-GHSKt-POT模型相比于其它异方差模型、简单SV类模型更具优势,而POT方法则能有效捕捉序列的尾部特征。我们这里将两者有效地结合,形成了新的VaR测度模型,为大多数带有尖峰厚尾、随机波动、异方差、杠杆效应等特征的金融资产的风险测度提供了更为实用的新方法。
[1] Barndorff-Nielsen.Exponentially Decreasing Distributions for the Logarithm of Particlesize[C].Proceedings of the Royal Society London A,1977.
[2] Joans Andresson.On the Normal Inverses Gaussian Stochastic Volatility Model[J].Journal of Bussiness of Economics Statistics,2001,19(1).
[3] Kim Shephard,Chib.Stochastic Volatility:Likelihood Inference and Comparison with ARCH models[J].Review of Economic Studies,1998,65(3).
[4] Ramazan G,Faruk S.Extreme Value Theory and Value-at-Risk:Relative Performance in Emerging Markets[J].International Journal of Orecasting,2004,20(2).
[5] 王春峰,万海晖,张维.金融市场风险测量模型——VaR[J].系统工程学报,2000,15(1).
[6] 林宇.基于双曲线记忆 HYGARCH模型的动态风险VaR测度能力研究[J].中国管理科学,2011,19(6).
[7] Yu J.On Leverage in a Stochastic Volatility Model[J].Journal of Econometrics,2005,127(2).
[8] Jouchi Nakajima,Yasuhiro Omori.Stochastic Volatility Model with Leverage and Asymmetrically Heavy-tailed Error Using GH Skew Student's t-distribution[J].Computational Statistics and Data Analysis,2010,56(11).
[9] Chib S,Jeliazkov I.Marginal Likelihood from the Metropolis_Hastings Output[J].Journal of the American Statistical Association,2001,96(453).
[10]Kim Shephard,Chib.Stochastic Volatility:Likelihood Inference and Comparison with ARCH Models[J].Review of Economic Studies,1998,65(3).
[11]McNeil A J,Frey R.Estimation of Tail-related Risk Measures for Heteroscedastic Financial Time Series:An Extreme Value Approach[J].Journal of Empirical Finance,2000,7(3).
[12]Pickands.Statistical Inference Using Extreme Order Statistics[J].Annals of Statistics,1975,3(1).
[13]朱慧明,林静.贝叶斯计量经济模型[M].北京:科学出版社,2009.
[14]Choulakian V,Stephens M A.Goodness-of-Fit Tests for the Generalized Pareto Distribution[J].Technometrics,2001,43(4).

