基于DDS相位噪声分析及抑制

姚宏亮， 汪海燕

0 引 言

直接数字频率合成器（DDS）概念出自1971年，直接数字频率合成器技术的问世，导致了频率合成器的第二次革命。DDS具有超宽的捷变速率、超高的相对宽带、超细的分辨率以及相位的连续性；极易实现各种调制，具有可编程性以及全数字化、便于单片集成等优越性能，从问世以来受到广泛关注，DDS应用领域非常广泛。

但是由于DDS其自身特点，决定其仍然存在缺点:分布难预测、杂散抑制差，这在很大程度上限制着DDS的应用。因此，杂散成为限制DDS技术应用的一个突出因素。早期国外多位专家学者对直接数字频率合成器杂散及其来源进行了研究和详细的分析，给出了诸多完善的方法:H T Nicholas［1］在1987年第一次对直接数字频率合成器的杂散在理论上进行了分析，并给出算法，提出了优化结构途径，设计并研制了高性能DDS。1993年至1994年，V F Kroupa，Harris等人分别利用对相位误差的级数表示、用噪声反馈方法以降低由DAC量化误差的方法，分析了直接数字频率合成器的杂散，提出了确定杂散的方法［2］。近几年，国内电子科技大学、南京理工大学等高校科研机构也对DDS杂散的分析、确定、抑制进行总结和研究。

1 DDS芯片中相位噪声恶化分析

1.1 DDS芯片中的主要杂散

DDS的基本原理框图如图1所示。

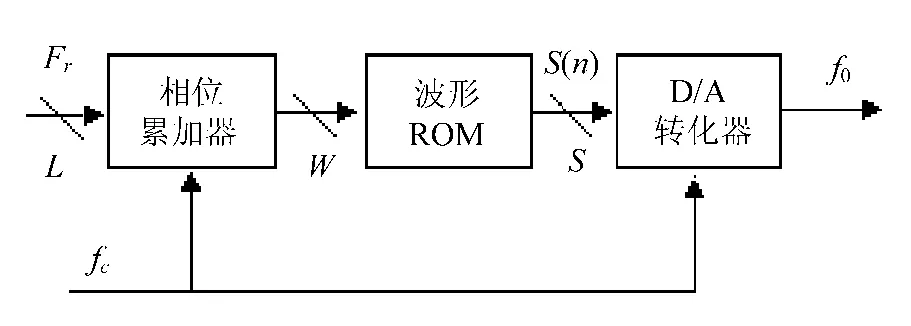
图1 DDS原理框图

图中，fc为参考时钟频率，Fr为频率控制字，字长为L（二进制，以下同），W 为相位累加器的字长，被相位累加器截断位数B＝L－W，ROM存储器输出幅度序列函数S（n），字长为S。直接数字频率合成器杂散主要来自以下几个方面:时钟泄漏；相位截断误差；ROM幅度量化误差；开关暂态引起的杂散；DAC的非线性转换误差。

1.2 相位截断对输出相噪的影响［3］

图1所示DDS输出频率为:

其输出的理想时域函数为:

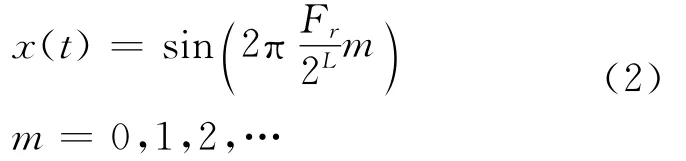
相位累加器产生相位截，忽略DAC性能，忽略ROM存储器的有限字长，显然DDS输出为

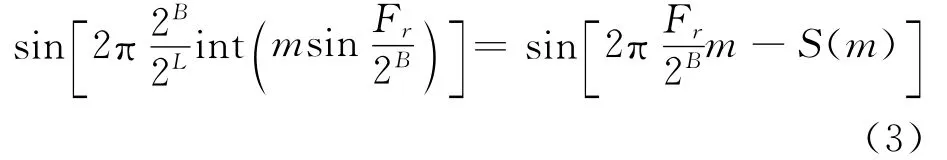
式中:int（－）——取整函数；

S（m）——相位累加器输出的误差序列函数。

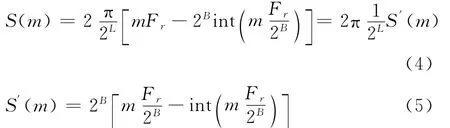
对一锯齿波函数S′（t）采样得到相位误差序列S′（m）。函数 S′（t）的周期、幅度分别为周期表达式内＜Fr＞2B为Fr模2B的余数，因为锯齿波函数S′（t）的周期与采样函数S′（m）的周期相左，锯齿波函数S′（t）周期大于或者等于采样函数S′（m）周期。所以，S′（m）周期表达式内（Fr，2B）为Fr和2B的最大公 约 数。那 么，S′（m）的 频 谱 是 以为间隔。因此，在频率范围内，直接数字频率合成器相位截断杂散谱线位置必须满足不等式

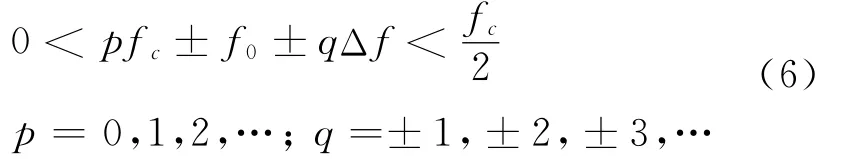
大多情况Fr为奇数，此时，由前述分析，S′（m）的周期为2B，如此就把S′（m）的周期改变为2BTc，由傅氏变换

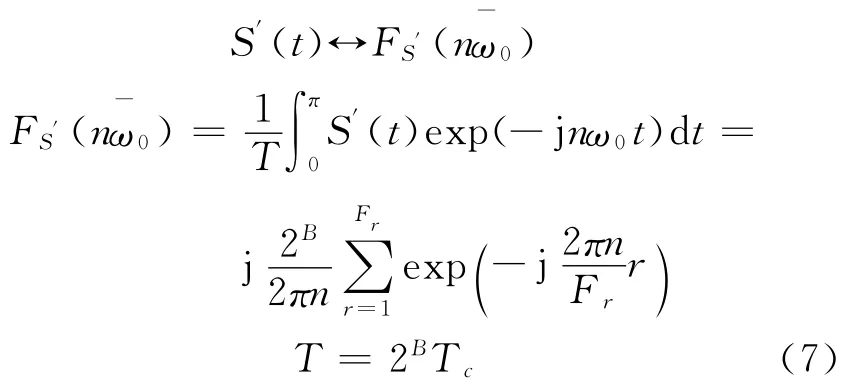
由式（4），（5），（7）得

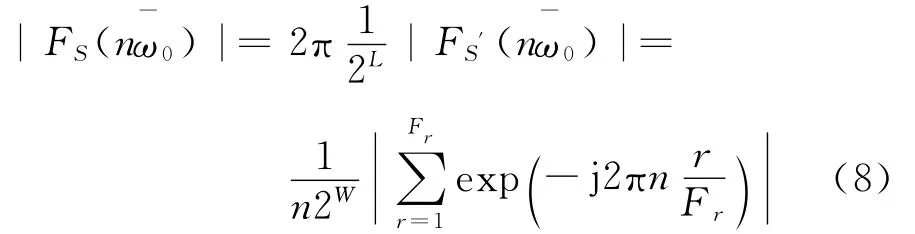
式（8）给出了直接数字频率合成器相位截断杂散的幅度以及位置。在此需要注意，式（8）给出DDS的杂散位置，幅度是基于对S′（t）周期扩大而进行的，从而避免单周期推导烦琐。

可见DDS中，由相位截断引起的输出相噪恶化很小。

1.3 ROM存储器有限字长对输出相噪的影响

当ROM采用S位二进制数保存正弦函数值时量化误差为:

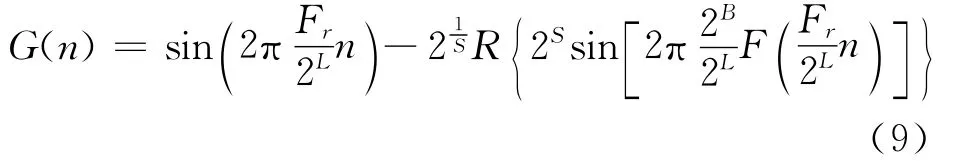
式中:R（x）——对x做最靠近x的取整函数。

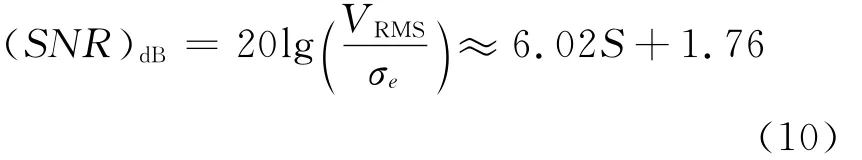
式（10）给出，当每增加一位量化位数S，那么信噪比将增加6dB。

1.4 DAC对相位噪声的影响

DAC非线性转换引起的量化噪声与ROM存储器有限字长的影响相同，仍然使用1.3中的结论。ROM存储器直接驱动直接数字频率合成器DAC，假设字长相同的情况下，输出相位噪声在式（10）基础上增加3dB。

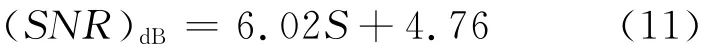
2 DDS相位噪声抑制方法

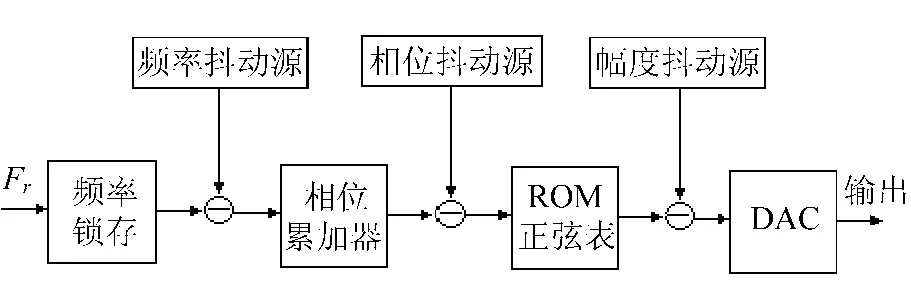
图2 DDS抖动注入方式

抖动注入的应用有多种方式:可以对D／A前的数据进行幅度加抖，即幅度抖动注入；可以对ROM的寻址地址加抖，即相位抖动注入；可以对输入的频率控制字Fr加抖，及频率抖动注入［4－5］。

文献［5-6］在理论上对几种抖动注入技术在直接数字频率合成器中的应用作了较深入的分析。文献［7］介绍了几种具体的抖动注入结构及其仿真。式（10）表示正常情况下每个ROM寻址位6dB的杂散，非减性（non subtractive）相位加抖增加了噪声基底，然而，结果可使杂散改善提高到每位12dB。非减性幅度加抖不仅改善杂散，同时杂散改善带来整体谱质提高，虽然付出抬高噪声基底，减小动态范围代价，但是完全值得，美国高通（Qualcomm）公司的Q2334即采用了幅度抖动注入技术的范例。

3 结 语

给出了一种推导分析直接数字频率合成器相位截断杂散的幅度以及位置的方法，详实分析了DDS中相位截断杂散的恶化、误差。相位截断对DDS的输出相噪影响很有限、DAC的内部噪声影响也不大；目前，真正制约DDS谱质性能的关键是DAC，DAC的位数、ROM有限字长决定直接数字频率合成器相位噪声，大小由式（11）给出。并介绍了近年来关于杂散抑制的一种主要技术与结构。除了抖动改善杂散，还有抑制杂散的方法:器件的选择、参考源的考虑、输出频段的选择等。文献［8］采用DDS技术生成高频超声波，进而合成次声波的方法。

［1］ H T Nicholas.An analysis of the output of direct digital fre2quency synthesizer in the presence of the phase accumulate truncation 41st［J］.AFFS，1987:495-502.

［2］ 张玉兴，彭清泉.DDS的背景杂散信号分析［J］.电子科技大学学报，1997，26（4）:362-365.

［3］ 张骏凌，张玉兴.直接数字频率合成器中的相位噪声分析［J］.电子科技大学学报，1999，28（1）:24-27.

［4］ M J Flanagan，G A Zimmerman.Spur-reduced digital sinusoid synthesis［J］.IEEE Trans.On COM.，1995，43（7）:128-136.

［5］ J Vankka.Spur reduction techniques in sine output direct digital synthesis［J］.IEEE Proc.50th AFCS，1996:951-959.

［6］ L J Kushner.The compo site DDS-A new direct digital synthesizer architecture［J］.IEEE Proc.47th AFCS，1993:255-260.

［7］ V S Reinhardt.Spur reduction techniques in direct digital synthesizers［J］.IEEE Proc.47th AFCS，1993:230-241.

［8］ 李林，田瑞，程凤芹，等.基于DDS技术的次声波合成方法［J］.长春工业大学学报:自然科学版，2009，30（5）:546-550.