群体多目标优化问题的α度联合有效解及最优性条件

陆 晶， 贺 莉， 魏彦吉， 刘庆怀＊

（1.长春工业大学 基础科学学院，吉林 长春 130012；2.吉林农业大学发展学院 基础部，吉林 长春 130600）

0 引 言

设有决策群体G＝｛DM1，DM2，…，DMl｝，其中DMr是第r（r＝1，2，…，l，l≥2）个决策者。考虑群体多目标优化问题:

文献［1］提出了多人多目标决策的均衡协调解，文献［2］给出了多目标群体决策的最优性条件，文献［3］利用供选方案的有效数引进一类基本的联合有效解概念，并给出了解的最优性必要条件，文献［4］给出了群体多目标决策联合有效解类的几个最优性充分条件，文献［5］给出求解群体多目标凸规划的一个交互规划算法，文献［6］提出了求解群体多指标决策问题的偏爱度法，文献［7］定义了一类带参数的α－较多联合有效解，同时得到了这类解的最优性必要条件和充分条件，文献［8-9］介绍了多目标和群体多目标理论。

由群体多目标优化（GMP）关于x∈X的有效数和弱有效数的定义可知，每个决策者对同一个方案所起的作用是相同的，即对同一个方案，每个决策者的偏爱是相同的。但是在现实世界中，每个决策者的偏爱是不可能一致的。对于同一个方案，每个决策者根据自己的经验、所接受教育的程度、对方案的了解深度、个人所研究的方向等不同，对同一个方案所起决定作用或重要性是不同的。因此，文中假设各个决策者对同一个方案的作用或重要性已排好序（第一个决策者的作用最大，第二个次之，依次下去），即按照作用的大小已经排序。从而相当于对于不同的决策者，都有相应的权序。记这个权序为H。

在这个假设条件下来定义群体多目标优化问题α度联合（弱）有效解，然后给出群体多目标优化问题的最优性必要条件。

1 基本概念

设共有l个决策者，且这l个决策者已经排好序。并把他们分成两组，把决策作用大的［l／3］个人分到第一组，其余的l－［l／3］个人分到第二组。

根据上述的分组方案，下面给出权序满意度。

定义1 设X≠Φ，x∈X，令

则称

是群体多目标问题（GMP）关于x的满意度。

定义2 设X≠Φ，x∈X，令

则称

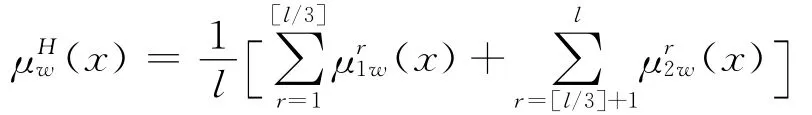
是群体多目标问题（GMP）关于x的弱满意度。

1）若μH（x～）≥α，则称x～是群体多目标优化问题（GMP）的α度联合有效解，其解集记作EHα（fG，X）。

2）若μHw（x～）≥α，则称x～是群体多目标优化问题（GMP）的α度联合弱有效解，其解集记作

由定义3易知，如果X是凸集，fr:X→Rmr（r＝1，2，…，l）是严格凸向量函数，则有

EHα（fG，X）＝EHαw（fG，X）

定义4 设X≠Φ，x∈X

1）若μH（x～）＝1，则称x～是群体多目标优化问题（GMP）的群体一致联合有效解。

定义5 设X≠φ，x∈X，α～＝0.5。

1）若μH（x～）≥0.5，则称x～是群体多目标优化问题（GMP）的可接受联合有效解，其解集记作

2）若μHw（x～）≥0.5，则称x～是群体多目标优化问题（GMP）的可接受联合弱有效解，其解集记作

文中给出的群体多目标问题（GMP）关于x的满意度和弱满意度的定义。这两个定义并不是绝对的，也可以选择其它的定义方法。

2 必要条件

下面给出问题（GMP）的α度联合有效解和α度联合弱有效解的Fritz-John型必要条件和Kuhn-Tucker型必要条件。

设群体多目标决策问题（GMP）的供选方案集X＝｛x∈Rn｜g（x）≤0，h（x）＝0｝非空，其中g:Rn→Rp和h:Rn→Rq在x～∈X处一阶可微。记L＝2｛1，2，…，l｝是由｛1，2，…，l｝中所有子集组成的幂集，而Lt＝｛Ω∈L｜｜Ω｜＝t｝，其中｜Ω｜表示集合Ω中元素的个数。

引理1 设x～∈X，x～是t个决策者的有效解，μH（x～）是群体多目标问题（GMP）关于x～的满意度，群体中对方案x～满意的个体集合为Ωt∈Lt，那么如果∃α∈［0，1］，满足μH（x～）≥α，则有

证明 因为

即

所以

因此有

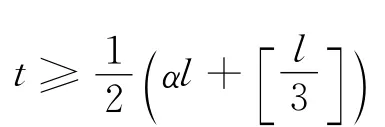
由于t是自然数，所以得到

定理1 （Fritz-John型必要条件）

设X≠Φ，fr:X→Rmr（mr≥2）（r＝1，2，…，l），g:Rn→Rp和h:Rn→Rq在x～∈X处一阶可微。若，则存在

以及

使得

对任意的r∈Ωt有x～∈Ew（fr，X）。因此，由多目标优化的Fritz-John型必要条件知，存在ω～r∈Rmr＋（r∈Ωt），λ～∈Rp＋，μ～∈Rq使得

对式（2）关于r求和，得

令

即得式（1）。

定理2 （Kuhn-Tucker型必要条件）

设X≠φ，fr:X→Rmr（mr≥2）（r＝1，2，…，l），g:Rn→Rp和h:Rn→Rq在x～∈X处一阶可微。若，X 在x～处满足 Kuhn-Tucker约束规格，则存在

以及

使得

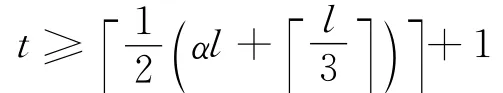
又因为X 在x～处满足Kuhn-Tucker约束规格，于是存在

使得对任意的r∈Ωt有x～∈Ew（fr，X）。因此，由Kuhn-Tucker型必要条件:存在

使得

对式（4）r求和得

令

即得式（3）。

3 结 语

给出了群体多目标优化问题的权序α度群体有效解和弱有效解的定义，同时还给出了解的最优性必要条件（Fritz-John型必要条件和Kuhn-Tucker型必要条件），并给出了证明。进一步还将给出解的最优性充分条件与算法等。

［1］ 祝世京，温鹏，陈延.多人多目标决策的均衡协调解［J］.系统工程学报，1993，8（1）:9-15.

［2］ 林锉云.多目标群体决策的最优性条件［J］.南昌大学学报，1995，19（1）:43-50.

［3］ 胡毓达.群体多目标决策的联合有效解类及其最优性条件［J］.上海交通大学学报，1999（6）:642-645.

［4］ 胡毓达，于丽英.群体多目标决策联合有效解类的几个最优性充分条件［J］.运筹学报，2000，4（4）:32-36.

［5］ 王晓敏.求解群体多目标凸规划的一个交互规划算法［J］.运筹学杂志，1996，15（1）:37-46.

［6］ 胡毓达，田川.求解群体多指标决策问题的偏爱度法［J］.系统工程理论与实践，1996，16（3）:52-56.

［7］ 杨雷，王中兴，于丽英.群体多目标决策α－较多联合有效解类的最优性条件［J］.贵州大学学报，2000，17（2）:69-81.

［8］ 胡毓达.多目标规划有效性理论［M］.上海:上海科学技术出版社，1994.

［9］ Lewis H S，Butler T W.Aninteractive framework for multipersen，multiobjective decision［J］.Decisin Sciences，1993，24（1）:1-22.

［10］ Huang C L，Lin M J.Group decision making under multiple criteria［M］.Berlin:Springer-Verlag，1987.