常微分方程初值问题的变分迭代算法

姜兆敏

（江苏理工学院 数理学院，江苏 常州 213001）

0 引 言

关于求微分方程近似解的分析方法很多，如摄动法、同伦分析法、同伦摄动法、变分迭代法、Adomian分裂算法等。其中，变分迭代法已经被成功地应用于解决各种线性、非线性问题［1－4］，许多研究者还对其进行了改进［5－6］，变分迭代法对求微分方程的近似解、精确解是一种很有效的方法。

文中主要考虑用变分迭代法求解如下n阶线性常微分方程的初值问题

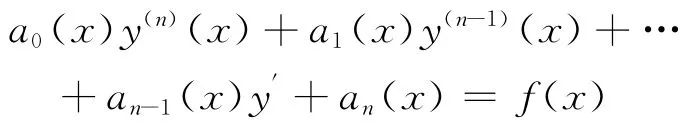
其中，a0（x），a1（x），…，an（x），f（x）为连续函数。初值条件

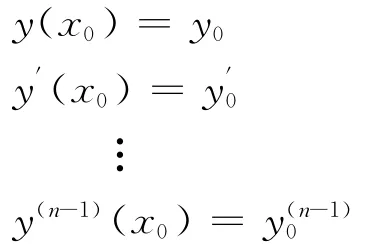
1 变分迭代法

为了阐明变分迭代法的思想，以下面形式的非线性微分方程为例说明

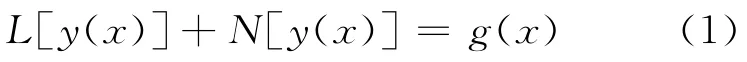
式中：L——线性算子；

N——非线性算子；

g（x）——连续函数。

方程（1）的校正泛函可表示为

式中：λ（t）——拉氏乘子，可以用校正泛函取驻值的条件来确定；

yn（x）——方程（1）的n阶近似解；

2 应用举例

例1 考虑一阶线性微分方程

初值条件

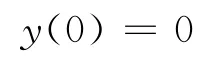
方程（3）的校正泛函为

对式（4）进行变分，得

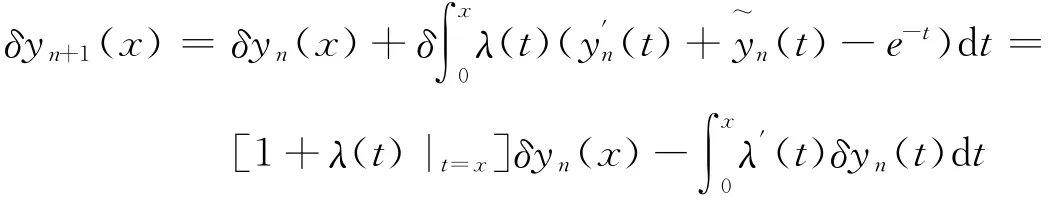
得到驻值条件：

于是可以识别拉氏乘子λ＝－1，将其代入式（4），得到以下迭代公式

取初始近似解y0（x）＝0，应用迭代公式（5），通过计算得：

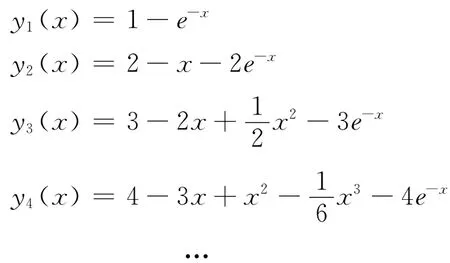
由于

所以

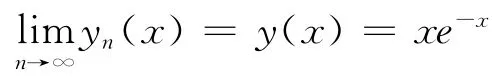
此为所求常微分方程初值问题的精确解。

例2 考虑二阶线性微分方程

初值条件：

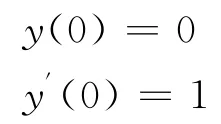
方程（6）的校正泛函为

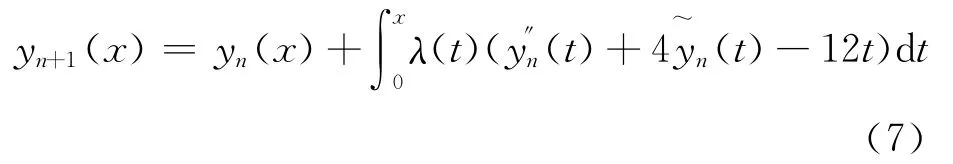
对式（7）进行变分，得

得到驻值条件

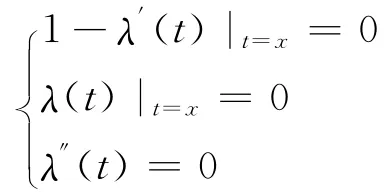
于是可以识别拉氏乘子λ＝t－x，将其代入式（7），得到以下迭代公式

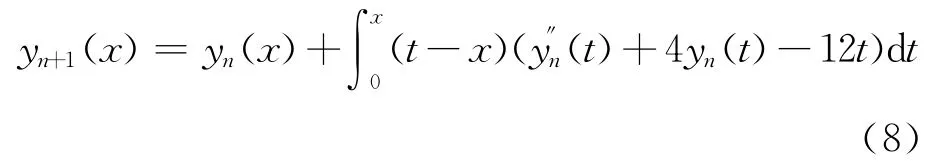
取初始近似解y0（x）＝x，应用迭代公式（8），通过计算得：

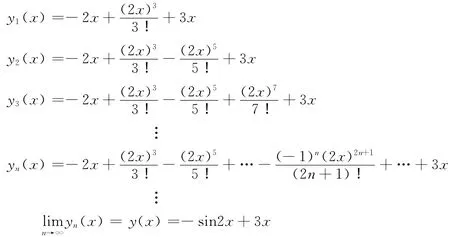
此为所求常微分方程（6）初值问题的精确解。

例3 考虑二阶柯西－欧拉方程

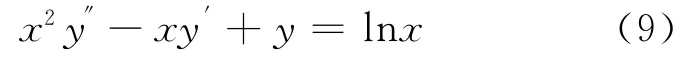
初值条件：

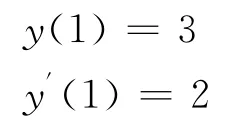
令

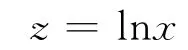
即

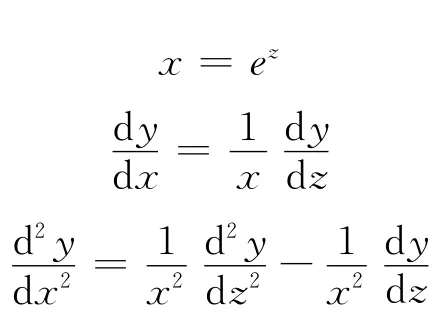
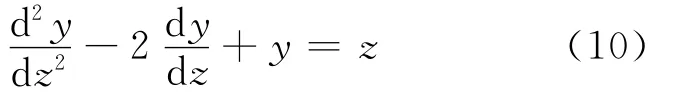
初值条件：

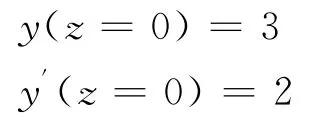
同例2，对方程（10）应用变分迭代法，得到以下迭代公式

取初始近似解

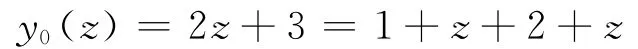
应用迭代公式（11），通过计算得：

原方程化为

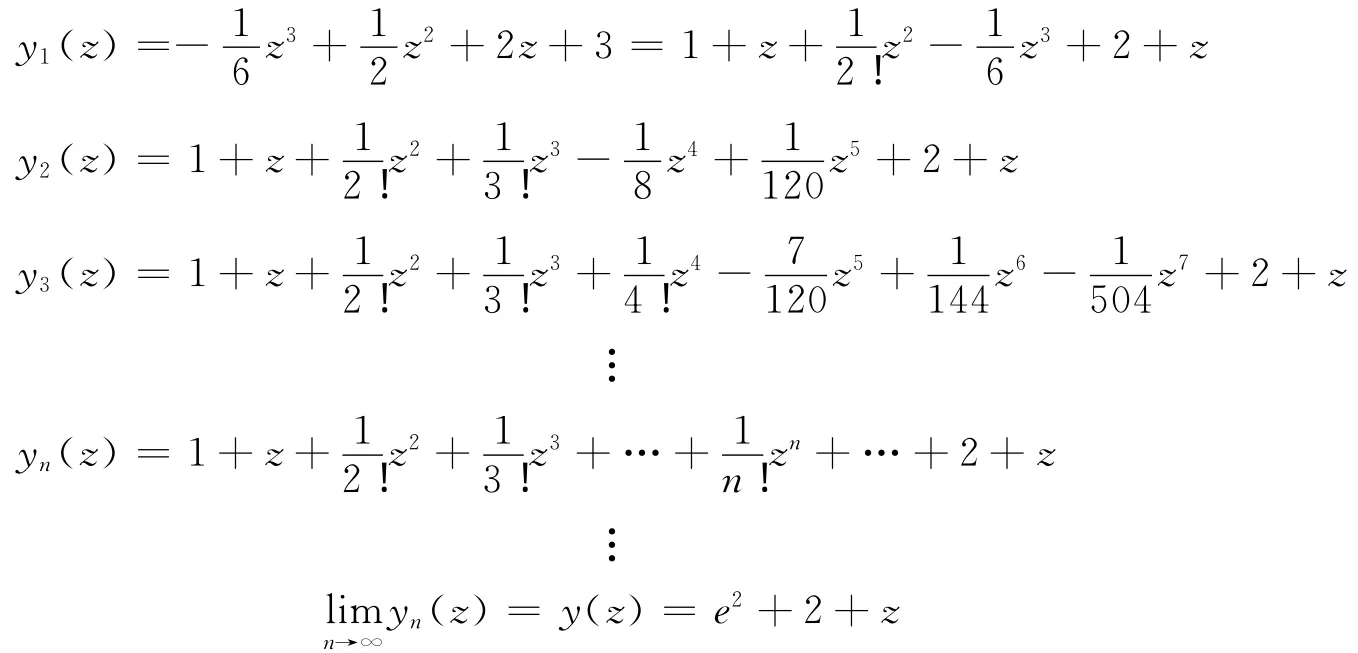
此为所求常微分方程（10）初值问题的精确解，从而原常微分方程（9）初值问题的精确解为

例4 考虑三阶线性微分方程

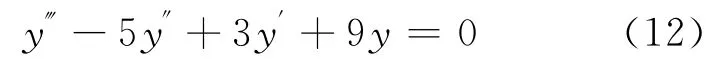
初值条件：

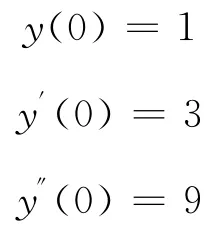
方程（12）的校正泛函为：

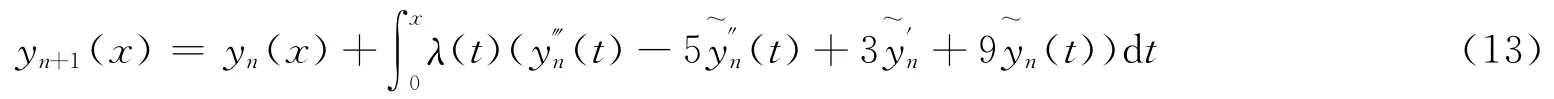
对式（13）进行变分，得：

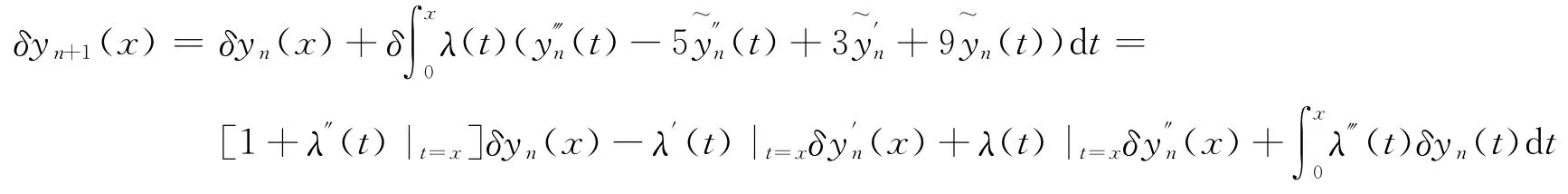
得到驻值条件：

于是可以识别拉氏乘子

取初始近似解

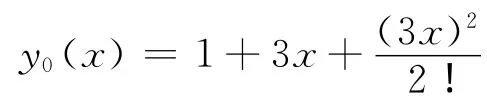
应用迭代公式（14），通过计算得：

此为所求常微分方程（12）初值问题的精确解。

3 结 语

用4个具体例子说明了变分迭代法在求解常微分方程初值问题中的应用，对于线性问题，使用变分迭代法可以确定拉格朗日乘子的精确值，从而给出有效的迭代公式。只要给出满足初值条件的初始近似解y0（x），利用变分迭代公式可以逐步提高近似解yn（x）的精度，当n→∞时，近似解yn（x）收敛到精确解。变分迭代法对求解常微分方程初值问题是一种很有效的分析方法。

［1］Ji Huan He，Xu Hong Wu.Variational iteration method：New development and applications［J］.Computers and Mathematics with Applications，2007，54：881－894.

［2］Zhang J.The numerical solution of fifth－order boundary value problems by the variational iteration method［J］.Computer and Mathematics with Applications，2009，58：2347－2350.

［3］Shang Xu Feng，Han Dan fu.Application of the variational iteration method for solving nth－order integro－differential equations［J］.Journal of Computational and Applied Mathematics，2010，234：1442－1447.

［4］Ganji D D，Hafez Tari，Bakhshi Jooybari M.Variational iteration method and homotopy perturbation method for nonlinear evolution equation［J］.Computer and Mathematics with Applications，2007，54：1018－1027.

［5］Ahmad Soltani L，Ahmad Shirzadi.A new modification of the variational iteration method［J］.Computer and Mathematics with Applications，2010，59：2528－2535.

［6］Hafez Tari.Modified variational iteration method［J］.Physics Letters A，2007，369：290－293.