基于双参数混合指数分布的参数估计
韩 静
(山西大学商务学院 理学系,山西 太原 030031)
0 引 言
寿命分析的目的是定量地把握系统或部件寿命的性状,并把所获取的信息反馈到设计、制造或使用维修中去,以期改善可靠性。从统计学的角度来看,可认为这些产品来自于不同的两个或多个子总体,我们称其为混合分布。基于极大似然估计(Maximum Likelihood Estimate,MLE)的方法能获得对参数较高精度的估计,因此极大似然法往往被用于混合分布的参数估计。EM算法虽然可研究混合分布在正常工作条件下的参数估计问题,但EM 算法可能会收敛到局部最优值[1-2]。针对极大似然估计计算量较大的缺陷,文献[3-4]结合遗传算法(Genetic Algorithm,GA)实现参数的优化估计。然而,遗传算法容易过早收敛产生早熟现象。为了克服其不足,文中将模拟退火技术(Simulated Annealing,SA)引入遗传算法中,基于极大似然估计模型利用退火遗传算法 (Simulated Annealing Genetic Algorithm,SAGA)实现寿命分布参数的最优估计。
1 极大似然函数法及其优化估计模型的建立[2]
设寿命分布为双参数混合指数分布,t1,t2,t3,…,tN是来自母体t的一个样本,定义其联合概率密度为:

即


其中,σi≥0,λi分别称为位置参数和尺度参数。记

一般采用二重或三重的混合(即i=2或3),多重混合之所以不常见,主要是模型参数过多,参数估计困难,也极少需要[5]。
当获得n个样本数据t1,t2,…,tn之后,样本的似然函数为:


要求得此极大似然估计值,传统的做法是直接将对数似然函数

关于各参数求偏导,使其为零,即
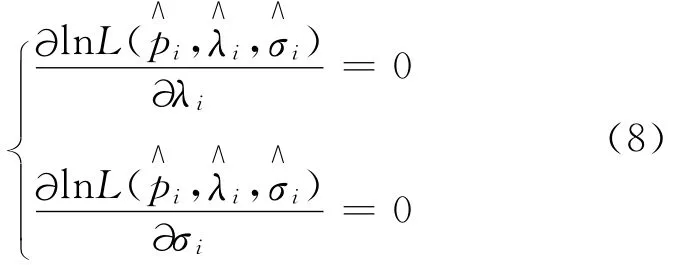
极大似然估计存在的问题是,对于许多具体问题不能构造似然函数解析式,或者似然函数表达式过于复杂而导致求解超越方程组(8)非常困难,因此必须借助于其它方法。下面介绍的退火遗传算法就是一种有效的方法。
2 模拟退火遗传算法[6]
退火遗传算法(Simulated Annealing Genetic Algorithm,SAGA),一般而言,首先考虑遗传算法GA和模拟退火算法SA两种算法,但是,这两种算法都各自具有本身的局限性。文中尝试将两种算法结合,丰富其优化过程,从而更有效率地搜索全局最优解。
退火遗传算法按以下主要步骤进行:
1)初始化控制参数,包括种群规模n,进化代数g,交叉概率pc,变异概率pm,温度下降因子δ,初始温度t0。
2)随机产生一个由确定长度的特征串组成的初始群体。采用实数编码,即每个染色体表示一个θ的估计,也就是说,每个染色体由s个基因位组成,第k个基因位表示θ的第k个分量(k=1,2,…,s),为方便记,以下将θ的分量统一用x表示,即θ=(x1,x2,…,xs),并将它与式(4)定义的θ等同对待。
3)计算每个个体xi的适应度函数值f(xi)。
4)根据适应度值生成新的下一代。
5)根据交叉概率pc和变异概率pm进行交叉与变异操作。
6)利用退火函数Tk+1=vTk,v∈(0,1)执行退火操作。
7)决策是否满足停止迭代的条件,如满足,输出最后结果。否则,转步骤3)。
8)算法结束。
3 应用实例
为了验证退火遗传算法在估计混合指数分布参数时的效率,文中提出的双参数指数混合分布模型在加速应力水平下寿命试验完全数据场合下进行了模拟,在计算机上产生了100个模拟数据[7]。
加速应力水平为S1=160K,S2=395K,S3=438K,S4=503K,正常应力水平S0=325K。采用Arrenius加速模型,在每一个应力水平上进行定数截尾寿命试验,得到一组模拟数据,其中ri为截尾数。
由数据的经验分布可知,符合指数类型分布模型如图1所示。

图1 数据的经验分布曲线
进行拟合优度检验。首先进行指数分布检验,结果见表1。

表1 基于χ2分布的拟合优度检验Ⅰ(单参数指数分布拟合)
其中,置信水平为α=0.1,拒绝域W= {χ2<
由表1可以看出,该数据不符合单一指数分布。接下来进行双参数指数分布拟合检验,结果见表2。

表2 基于χ2分布的拟合优度检验Ⅱ(双参数指数分布拟合)
由表2可以看出,该分布也不能用单一的双参数指数分布来表示。
记θ=[p,q,λ1,λ2,σ1,σ2],这里,选取 p=0.6,λ1=0.5,λ2=0.6,σ1=2,σ2=2.5,分别取种群大小n=20,40,60,80,100(即样本数目),最大进化代数为5 000;交叉概率pc=0.5;变异概率pm=0.05;采用算术交叉和非均匀变异,非均匀变异的系统参数为0.01;初始温度t0=100℃,温度冷却系数δ=0.95,利用提出的退火遗传算法对混合分布的极大似然模型进行参数估计。分别在样本容量为20,40,60,80,100的时候各重复1 000次试验。第i次试验得到的估计记为

则


估计结果及误差见表3。

表3 完全数据场合下的估计结果
由表3可以看出,文中采用退火遗传算法解决极大似然优化估计问题,所得到的寿命分布参数与真值几乎吻合,随着样本的增加,估计也越准确,从而证明了文中所提出的方法的有效性。
4 结 语
基于最大似然估计法和优化理论的基本原理以对数似然函数为目标函数,建立了可靠性寿命分布参数的最大似然估计模型,并使用退火遗传算法求解。该方法既可以克服传统优化技术易陷入局部最优解的缺点,又能够改善遗传算法容易早熟的局限性。文中提出的方法具有普遍适用性,可由计算机软件实现,计算精度和效率较高,适用于各种仪器及电工电子元件的可靠性寿命分布参数的估计。
[1] 张士峰.混合正态分布参数极大似然估计的EM算法[J].飞行器测控学报,2004,23(4):125-128.
[2] 王建康,盖钧镒.混合分布理论及应用[J].生物数学学报,1995,10(3):67-70.
[3] 方华元,胡昌花,李瑛.基于遗传算法的威布尔分布的参数估计及MATLAB实现[J].战术导弹控制技术,2007,15(1):100-103.
[4] 方华元,胡昌华,樊红东,等.基于GA的可靠性寿命分布参数的极大似然优化估计[J].上海航天,2006,23(2):50-53.
[5] Euan W,Mc Gookin,David J,et al.Submarine manoeuvring controllers'optimisation using simulated annealing and genetic algorithms[J].Control Engineering Practice,2006,14(1):1-15.
[6] 孙雅芳,王晓丹,徐俊彦,等.基于视觉认知的全局优化算法[J].长春工业大学学报:自然科学版,2010,31(6):609-612.
[7] Marvin A,Arostegui Jr,Sukran N,et al.An empirical comparison of tabu search,simulated annealing,and genetic algorithm for facilities location problem[J].International Journal of Production E-conomics,2006,103(2):742-754.

