结合过完备字典与PCA的小样本语音情感识别方法

毛启容，赵小蕾，白李娟，王治锋，詹永照

(江苏大学计算机科学与通信工程学院，江苏 镇江 212013)

计算机技术与人机交互技术的日益发展，赋予计算机感知、理解、识别和生成人类情感的能力，使人机交互变得更加友好、智能、和谐，这已成为信息科学领域中的前沿热点问题.语音情感识别作为人机交互的研究热点之一，其通过提取语音信号中的情感特征，判断说话者的喜怒哀乐，而且国内外在这一领域的研究已取得许多突破性的成果.近年来，信号的稀疏表示引起越来越多研究者的兴趣，由于其优良特性，信号稀疏表示已经被应用到信号处理的许多方面，如压缩［1］、反问题的正则化［2］、信号去燥［3］、信号编码［4］、识别［5］、融合技术［6］等.稀疏分解可以实现数据压缩的高效性，更重要的是随着冗余字典的提出可以利用字典的冗余特性捕捉信号内在的本质特征.

过完备信号稀疏表示方法始于20世纪90年代，1993年 Stephane G.Mallat和 Zhang Zhifeng首次提出应用过完备冗余字典对信号进行稀疏分解的思想，过完备冗余字典的提出为后来学者的研究提供了理论基础，如文献［7］提出的基于词典学习和稀疏表示的超分辨率的方法，文献［8］提出的一种基于超完备字典学习的图像去噪方法等.而且通过信号在过完备冗余字典上的分解，来表示信号的基可以自适应地根据信号本身的特点灵活选取.这将使得稀疏表示方法可以更好地应用于模式识别领域.其中最有代表性的是A.Y.Yang等［9］结合压缩感知理论提出了稀疏表示识别算法(sparse representation recognition，SRR)，并应用于人脸识别，得到很高的识别率.稀疏表示方法拥有优良的特性，但近几年的研究大多局限于大样本数据库.且在模式识别领域中，随着特征维数的增加，特征冗余度与系统复杂度会随之增加，在运用稀疏表示识别时，识别率不高且需要大量训练样本进行训练，给试验研究带来了不便.为了解决这个问题，文中将PCA降维方法与过完备字典运用到SRR识别方法中，提出了结合过完备字典与PCA的小样本语音情感识别算法(recognition of speech emotion on small samples by over-complete dictionary learning and pca dimension reduction，RSESS-ODP)，以达到提高识别率并使其更适用于小样本数据库的试验目的.文中使用小样本语音情感数据库进行测试，并在其基础上与较成熟的识别模型BP，SVM作比较，来验证文中方法的有效性.同时，为了进一步探索如何减少时空复杂度与提高识别率，在验证SRR有效性后，鉴于稀疏表示作为一种新的特征表示方法，文中随后探索稀疏化后特征对系统性能的影响.以往语音情感识别技术大多基于传统特征，虽然传统特征经过优化(如遗传算法、粒子群算法等)与降维方法(如PCA、LDA等)的处理，将高维特征空间映射到低维特征空间，所得的有效特征数据可提高识别率、降低系统复杂度，但随着维数的逐渐增加不能有效权衡识别率与时空复杂度的关系.如果稀疏化特征表示形式更具优势，那将对日后的试验研究提供更佳输入数据.

文中拟通过使用K-SVD算法与OMP算法对语音情感信号传统特征进行稀疏分解，给出基于小样本语音情感数据库的语音情感特征的稀疏表示方法以及RSESS-ODP算法.为验证RSESS-ODP算法的有效性，将其与BP和SVM进行比较，并分析稀疏化前后特征在使用各种分类器下对识别率、时间效率、空间效率等性能的影响.

1 语音情感特征的稀疏表示方法

过完备字典可以通过赋特定的函数集如wavelate，curvelet，contourle等函数得到，也可以设计算法通过不断迭代自适应给定的信号样本集，得到更符合信号特性的过完备字典［10］.文献［2］首次提出了K-SVD算法，此算法通过自适应信号样本集合训练得到过完备字典，其是K-均值聚类算法的扩展算法.该算法通过不断迭代稀疏编码，为更好地符合样本固有特性而不断地更新字典，最终得到有效的过完备字典.文中使用文献［10］提出的有效K-SVD算法训练包含语音情感信号主要特征的冗余字典，此算法可减少稀疏分解的计算量，从而减少信号稀疏分解的系统运行时间.

1993 年，Y.C.Pati等［11］提出了正交匹配跟踪(orthogonal matching pursuit，OMP)的概念，OMP 算法在MP算法的基础上将所构原子按Gram-Schmidt正交化方法进行正交化处理.利用OMP算法可保证在有限次迭代次数后逼近误差衰减到0.OMP算法是贪心算法，每次迭代选择与当前剩余信号最大相关的原子信号，选择的原子与已选中的原子集正交化，而当前剩余信号被重新计算，进入下一次迭代，直至达到所设定的终止条件为止.用OMP算法可得到信号的近似线性组合.

本节将介绍如何求得语音情感信号特征的稀疏表示.利用文献［10］中的有效K-SVD算法训练符合语音情感信号固有特性的自适应冗余字典，字典的维数假设为M×N维，其中，M在这里是指语音情感特征维数，N代表语音情感过完备字典原子个数，并满足N≫M或N＞M的条件;用文献［10］中提到的OMP算法求得语音信号的稀疏编码.

定义各符号含义如下:D为过完备字典;D0为初始字典;Y为语音情感信号特征集，Y集合每一列代表一个语音情感样本所有特征;y为Y中一个样本特征集合;α为样本信号特征y的稀疏表示;X为信号的稀疏表示集合，x为一个样本特征的稀疏表示向量;d为D中原子，dk为D中第k个原子;Dj为过完备字典D中的第j个原子，重新赋值后的原子;gT为新的稀疏表示系数;K为目标稀疏度，此为算法终止条件，稀疏度达到K值则算法终止;R为样本特征剩余值;I为使用第j个原子的语音情感样本信号索引;U为选中的原子索引集合.应用在语音情感特征稀疏表示方法中的具体步骤如下所示:

1)首先在Matlab下提取所有语音情感样本信号的特征，设特征维数为M维，样本个数为S个，则经特征提取后所得特征集合Y，大小为M×S.在Y集合中随机选取N个样本，赋值给初始字典D0，此时D=D0，其维数为M×N，同时将U初始化为空.

2)固定语音情感过完备字典D，求语音情感样本特征的稀疏表示集合X.根据公式(1)得到与原语音情感特征最相关的原子索引j，将j添加到U中，如果U非空并将其与U中其他原子正交化.根据公式(2)重新计算当前剩余语音情感特征的值记为R.

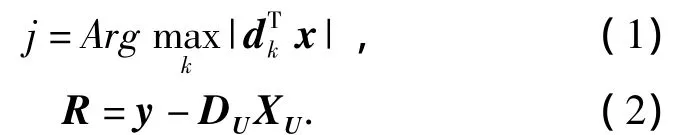
反复迭代步骤2)，当R小于一定阈值时，则终止步骤2).如果达到目标稀疏度K值，则执行步骤5)，否则执行步骤3).

3)固定稀疏表示集合X，根据公式(3)－(5)逐次优化D中的原子.

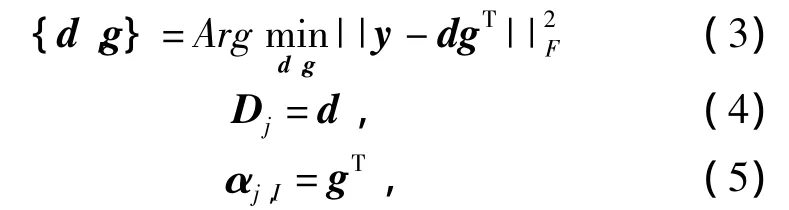
式中:d代表新的原子;g代表新得到的稀疏表示;T符号代表转置.反复迭代步骤3)直至遍历所有原子.

4)转入步骤2).重新计算语音情感特征的稀疏表示集合X.

5)算法结束.最终得到试验所需的语音情感过完备字典D与稀疏矩阵X.

2 RSESS-ODP算法

为了提高识别率和便于在小样本语音情感数据库中应用稀疏表示识别方法，文中将训练样本与测试样本特征使用PCA降维方法降维，以满足过完备字典N＞M的条件.并将建立试验来确定识别率最高的特征维数.在小样本语音情感数据库中，RSESS-ODP算法语音情感识别具体过程如下:

1)用PCA降维方法对训练样本和测试样本的语音情感特征降维，降到目标维数d维，其中d＜N，N为所训练的过完备字典原子个数.

2)应用第1节语音情感特征稀疏表示方法训练过完备字典，并基于此过完备字典求得经PCA降维后的语音情感特征的稀疏表示形式.即，假设情感类别数为C，则分别为每类情感训练一个过完备字典，这 C 个过完备字典 Di(i=1，2，3，…，C)，大小均为d×N，用此C类字典稀疏化各自情感类别的测试样本语音情感特征.

3)根据公式(6)，将稀疏化后的每个测试样本的语音情感特征经过所属类别的过完备字典进行变换，随后，将反变换后的Di×x向量与原信号之间的距离之差作为信号的冗余误差，如公式(7)所示，使用哪类过完备字典变换后所得误差最小，样本就归为哪一类.

式中:y为测试样本;xi为经稀疏分解后的稀疏向量;ei为所求得的冗余误差.

4)求得C类情感识别率ri.假设ti为正确分类样本个数，si为测试样本个数，则 ri=ti/si(i=1，2，3，…，C).

5)算法结束.

3 试验结果与分析

文中使用的语音情感数据库，由本课题组录制，包含6类典型情感，分别为高兴(happiness)、伤心(sadness)、惊讶(surprise)、生气(anger)、害怕(fear)和厌恶(disgust).每类情感录制了100个训练样本和30个测试样本，即训练集合共600句，测试集合共有180句.文中用Matlab提取共振峰、短时能量、基频、短时过零率等101维语音情感特征.

3.1 RSESS-ODP中误差计算方法的确定

在RSESS-ODP算法实现的过程中，求RSESSODP冗余误差的方法有多种，为使得RSESS-ODP算法达到最佳性能，分别计算不同距离计算冗余误差后所求得的情感识别率，从而找到计算冗余误差的最佳距离计算公式.

设有两个样本，xi=［xi1，xi2，xi3，…，xin］T和xj=［xj1，xj2，xj3，…，xjn］T，常用的求解向量距离的方法有如下几种.

1)欧式距离:

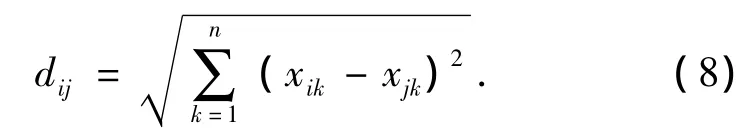
2)绝对值距离:

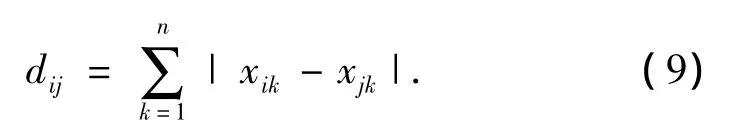
3)切比雪夫距离:

2017年我国木质家具出口数量25 603.69万件，其中出口美国9 860.3万件，占38.51%;木质家具出口金额137.33亿美元，其中美国42.83亿美元，占31.19%。

4)马哈拉诺比斯距离:

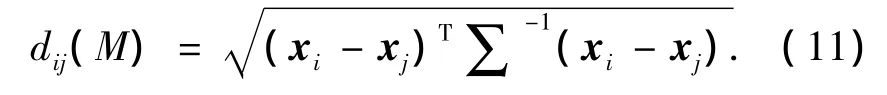
5)夹角:

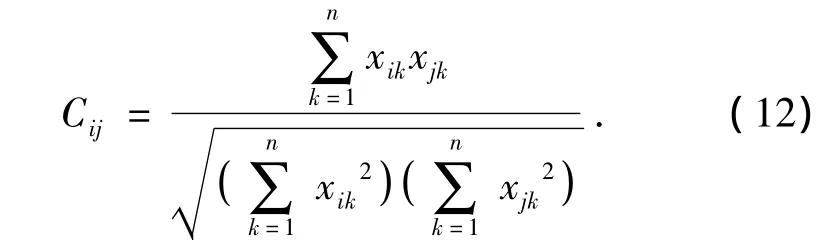
6)相关度:

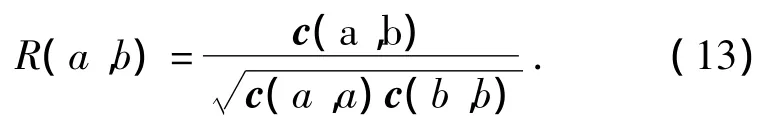
其中，c表示向量xi与xj的协方差矩阵，两个向量情况下，a=1，b=2，R值越大，则向量相似度越大.

为测试哪种距离更适合求解RSESS-ODP冗余误差，文中在Matlab环境下，以步长5取20到100维数，计算每个维数下RSESS-ODP算法使用不同距离公式得到的识别率情况，每个维数每个距离计算10次，并取平均值，最终结果如图1所示.

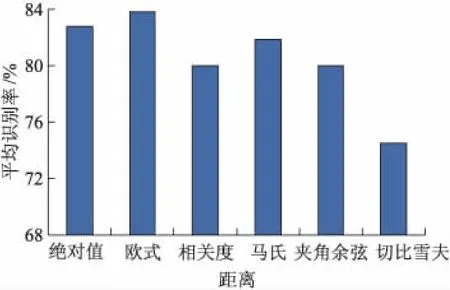
图1 使用不同距离时RSESS-ODP平均识别率对比

由图1可见，应用欧式距离求解冗余误差得到的平均识别率最高.欧式距离是m维空间中两个点的真实距离，其更能准确表达两点距离，更具有区分性.绝对值距离公式次之，但绝对值距离只是单纯地求解向量之间差值的绝对值，不能准确反映两点之间的距离，其他距离区分度稍低些.因此，RSESSODP算法选用欧式距离求解冗余误差.

3.2 不同识别方法的性能比较与分析

为验证文中所提算法RSESS-ODP的有效性，分别从识别率、时空效率的角度分析比较各识别方法的性能.

在基于过完备字典与PCA的语音情感稀疏表示识别方法中，经PCA方法降维后，不同的目标维数会得到不同的识别率.文中以维数间距等于5的步长求解不同维数下使用不同识别方法的平均识别率.为了验证RSESS-ODP在文中所用的小样本语音情感数据库上的识别有效性，在同一小样本语音情感数据库下，分别应用基本分类器“一对一”SVM、自主学习BP模型求得与RSESS-ODP相同维数的6类情感平均识别率.其中，SVM分类器使用径向基核函数，Gamma，C的值分别取0.01和8.5，而BP隐层节点数选择15.其识别结果对比情况如图2所示.

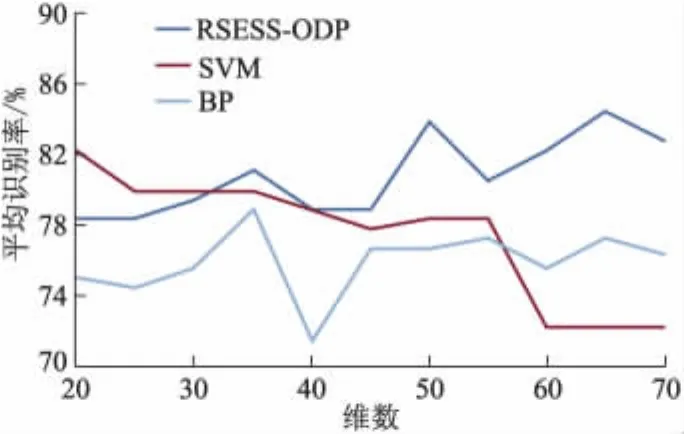
图2 RSESS-ODP、SVM、BP在不同维数下的识别率对比

由图2可知，维数为65维RSESS-ODP测得的6类情感平均识别率最高，运用RSESS-ODP识别算法识别率最高可达84.45%，平均识别率为81.47%;SVM最高识别率为82.22%，SVM的平均识别率为78.84%;而应用 BP算法，测得的最高识别率为78.89%，平均识别率为 75.73%.

根据上述分析可知，从最高识别率来看，SVM高出 BP 3.33%，RSESS-ODP 高于 SVM 2.23%;从平均识别率来看，SVM高出BP 3.11%，而RSESSODP高出 SVM 2.63%.换言之，RSESS-ODP略优于SVM，SVM略优于BP.综上所述，RSESS-ODP在小样本语音情感数据库中可达到较高识别率，且在语音情感识别中，从识别率角度分析，其具有较好的优势.

3.2.2 时间、空间运行效率分析

下面分别从时间与空间效率的角度进一步分析RSESS-ODP算法在小样本语音情感识别中的有效性.试验测得的运行时间与存储空间，是在同一台仪器上进行，使用每类情感100个训练样本以及每类情感30个测试样本得到的10次试验的平均值.表1给出了不同识别方法训练与识别过程所用的时间.

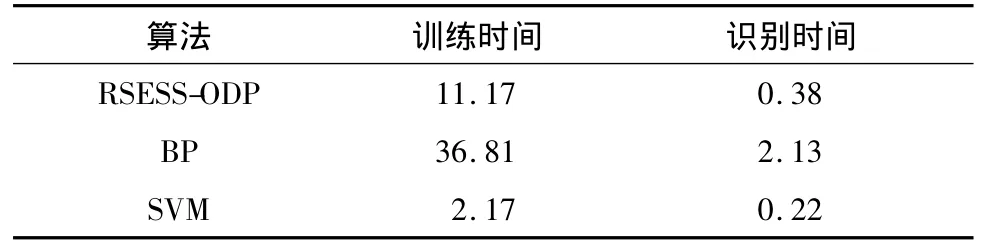
表1 不同识别方法所需的运行时间 s

从表1可见时间效率最高的是SVM方法，其次是文中所提出的RSESS-ODP方法.RSESS-ODP方法从训练过完备字典到稀疏分解语音情感特征平均所用的时间是BP训练时间的1/3，且识别时间比BP少1.05 s.从空间效率上分析，RSESS-ODP方法需要存储过完备字典与稀疏系数矩阵，BP，SVM以及距离分类器均需要存储样本语音情感特征.RSESS-ODP算法训练6类过完备字典，每个过完备字典维数为65×80，则共需存储过完备字典65×480维的矩阵，而稀疏系数矩阵只需存储非0元素，文中所用稀疏度为15，则系数系数矩阵共需存储15×780维的矩阵.而其他识别方法，需要存储65×780维的矩阵，所以从存储效率上来说，文中所提方法空间利用率略高.

从上述的识别率、时空效率分析来看，与其他识别方法相比，RSESS-ODP算法平均识别率与空间利用率最高.鉴于RSESS-ODP算法的优越性能，随后文中尝试使用稀疏化后的特征进行识别，以尝试提高各识别方法在小样本语音情感识别上的性能.

3.3 语音情感特征稀疏化前后算法性能分析

在第3.1和3.2节中，为了应用RSESS-ODP算法，分别用6类情感训练样本特征训练了6个过完备字典，在6类过完备字典上分别对各自情感测试样本特征进行稀疏分解.如果使用在6个过完备字典基础上稀疏化后的特征作为各分类器的输入，理论上来说这并不合理.这是由于稀疏化后的特征表示，是在过完备字典的基础上的稀疏变换系数矩阵，字典不同变换系数将不同，导致重复性会很大，区分度会很低.为了验证这一点，文中在RSESS-ODP中识别率最高的65维特征下，用BP做了相关试验，识别结果如表2所示.

表2 稀疏化特征识别率 %

从表2可见，若要将稀疏化后的特征作为各分类器的输入，必须使用统一的过完备字典.以下试验均使用PCA方法降维到65维数下进行，训练的统一过完备字典大小为65×120.用第1节方法对训练样本与测试样本特征进行稀疏分解，得到稀疏化后训练样本特征矩阵与测试样本特征矩阵大小分别为120×600和120×180.下面分别从识别率、时间效率、空间效率的角度分析比较各种分类器使用稀疏化前后特征的性能，从而验证使用稀疏化后特征可提高识别方法性能的假设.

3.3.1 语音情感识别率分析

文中使用的分类器有SVM模型、BP模型以及各种基于距离的分类器(如欧式距离、绝对值距离、切比雪夫距离、马哈拉诺比斯距离等).将稀疏化前后特征分别用于各种分类器识别试验中，各识别方法所得识别率情况如图3所示.

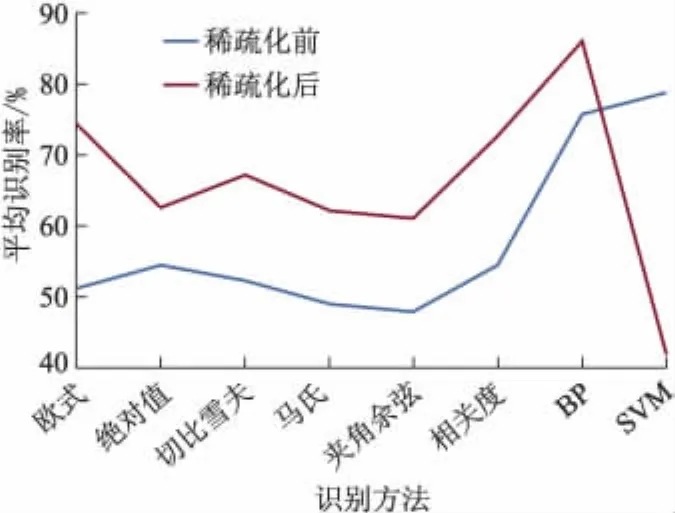
图3 各距离分类器使用稀疏化前后特征对比

从图3可见，除SVM外的分类器使用稀疏化后的特征比使用稀疏化前的特征求得的识别率更高，平均提高15%，且得到的识别结果较稀疏化前的特征的识别结果稳定.由于BP是自主学习，给定学习目标值后，经过逼近训练，得到各个情感类别的模型，虽然信号经过稀疏表示会存在一定的误差，但其并不影响类别之间的区分性，试验表明经过稀疏化的特征更具有区分性，故识别率更高.使用距离分类器时，根据测试样本与训练样本的相似性大小进行分类，与哪类测试样本相似程度大就归为哪一类别，使用稀疏化后的特征比使用稀疏化前的特征进行识别，得到的识别率更高，说明稀疏化后的数据具有明显的分类布局.稀疏化后的特征经过SVM模型训练识别得到的识别率较稀疏化前的特征经SVM训练识别得到的识别率低，平均识别率低36%，这说明稀疏化后的特征向量经SVM映射到更高维的空间，样本与样本之间的分散度很大，且区分度很低，类内距离与类间距离区分度不明显.这可能是经稀疏化后的向量，很多元素为0的缘故，再经过SVM映射到更高维空间则样本分类不明显.从图3亦可见，稀疏化前SVM识别率最高，可达78.84%，而稀疏化后BP识别率最高，可达86.12%，较稀疏化前的SVM识别率高 7.28%，同时也高于 3.2节中RSESS-ODP算法4.65%.换言之，稀疏化后特征应用于BP方法能得到更高的识别率.

3.3.2 时间、空间运行效率分析

从时间运行效率的角度分析，不同识别方法使用稀疏化前后特征平均运行时间如表3所示.

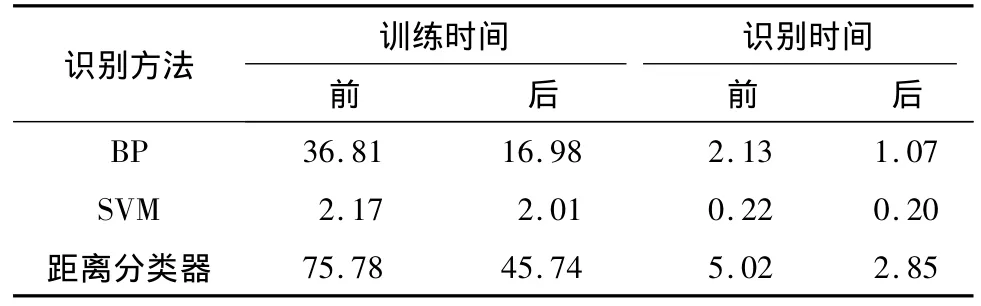
表3 稀疏化前后特征时训练与识别时间对比 s

由表3可见，使用稀疏化后特征各识别方法训练与识别时间均有所减少，变化幅度最大的为BP识别方法，其训练与识别时间极大缩短，是原来的1/2倍，其次是距离分类器，缩短近原来的1/2倍，而SVM没有明显变化，但也有所减少.总体来看，时间效率提升近原来的一半.空间效率分析同3.2.2的分析，经过稀疏表示可极大地节省存储空间，即使特征维数再大也便于存储处理.由此看来，稀疏化后的特征较稀疏化前的特征有更高的空间效率.

综上所述，可以得出如下结论:稀疏化的特征更有利于BP、基于距离的分类器的处理，而不适合SVM.总体上来说稀疏化后的特征适用于大多数分类器，且可提高分类器的整体性能.

4 结论

1)将稀疏表示与PCA相结合运用于小样本语音情感数据库进行识别，进一步验证了SRR算法的有效性，且经过试验验证较SVM与BP优越.

2)稀疏表示作为特征的另一种表示形式，稀疏化后的特征作为一种新的数据输入，可大幅度提高系统性能(如识别率，时间效率，空间效率等).其中，平均识别率提高约15%，在同等维数下时间效率提升近1/2，而空间效率提升近原来的1/3.

3)若想RSESS-ODP得到更高识别率，若想稀疏化特征进一步提高系统性能，则需继续提高稀疏表示的精确性与稳定性.

References)

［1］Bryt O，Elad M.Compression of facial images using the K-SVD algorithm［J］.Journal of Visual Communication and Image Representation，2008，19(4):270 －282.

［2］Aharon M，Elad M，Bruckstein A.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation［J］.IEEE Transactions on Signal Processing，2006，54(11):4311－4322.

［3］Protter M，Elad M.Image sequence denoising via sparse and redundant representations［J］.IEEE Transactions on Image Processing，2009，18(1):27－35.

［4］张新鹏，王朔中.基于稀疏表示的密写编码［J］.电子学报，2007，35(10):1892 －1896.Zhang Xinpeng，Wang Shuozhong.Steganographic encoding based on sparse representation［J］.Acta Electronica Sinica，2007，35(10):1892－1896.(in Chinese)

［5］晏 哲.基于稀疏性的人脸检测与识别方法研究［D］.西安:西安电子科技大学电子工程学院，2010.

［6］黄 影.基于正交匹配跟踪以及K-SVD的图像融合技术［D］.北京:华北电力大学电气与电子工程学院，2009.

［7］浦 剑，张军平.基于词典学习和稀疏表示的超分辨率方法［J］.模式识别与人工智能，2010，23(3):335－340.Pu Jian，Zhang Junping.Super-resolution through dictionary learning and sparse representation［J］.Pattern Recognition and Artificial Intelligence，2010，23(3):335－340.(in Chinese)

［8］蔡泽民，赖剑煌.一种基于超完备字典学习的图像去噪方法［J］.电子学报，2009，37(2):347 －350.Cai Zemin，Lai Jianhuang.An over-complete learned dictionary-based image denoising method［J］.Acta Electronica Sinica，2009，37(2):347－350.(in Chinese)

［9］Yang A Y，Wright J，Ma Y，et al.Feature selection in face recognition:a sparse representation perspective［R］.UC Berkeley Technical Report UCB/EECS－2007－99，2007.

［10］Rubinstein R，Zibulevsky M，Elad M.Efficient implementation of the K-SVD algorithm using batch orthogonal matching pursuit［R］.CS Technical Report，Technion，Israel Institute of Technology，2008.

［11］Pati Y C，Rezaiifar R，Krishnaprasad P S.Orthogonal matching pursuit:recursive function approximation with applications to wavelet decomposition［C］∥Proceedings of the 27th Asilomar Conference on Signals，Systems ＆Computers.CA:IEEE，1993:40 －44.