踏板行程模拟器在线控制动系统中的应用
宋传学,郑竹安,靳立强,彭思仑,王剑锋,肖 峰
(吉林大学汽车仿真与控制国家重点实验室,吉林 长春 130022)
随着线控制动系统的深入研究,一方面要提高制动安全性,另一方面要优化制动过程提高制动舒适度.制动踏板感觉是线控制动系统核心内容之一,它直接关系到车辆制动安全和驾驶舒适度.制动踏板感觉是制动踏板机构给驾驶员右脚的反馈作用,但在传统纯液压制动系统中启动防抱死操作时,会对制动踏板感觉产生不良的影响,甚至导致制动不平顺等问题.
为了解决此类问题,消除制动操作时的不适感,国内外学者对这方面都有所研究.D.G.Ebert等[1]提出用制动感觉因子BFI来主观评价制动踏板感觉,包括了踏板回位弹簧预紧力、踏板力、踏板位移等参数的影响,BFI指数方法计算简单且参数易于确定,但存在的困难在于制动器响应时间较难获得.A.J.Day等[2]对乘用车制动踏板感觉进行了预测,较好地分析了各个部件的关联性,但没有进一步改善制动踏板感觉.郑宏宇等[3]对线控制动系统踏板力进行了模拟研究,得出了与传统制动系统相仿的特性曲线,但结构相对复杂,在实车上的应用需要考虑失效情况和控制系统的响应时间.基于以上研究成果,笔者通过配备踏板行程模拟器,它内置弹簧支撑的柱塞,通过该柱塞的移动可以实现踏板感应,同时实现踏板反力.通过研究踏板行程模拟器,建立AMESim模型,并与Matlab/Simulink联合仿真,根据传统制动系统踏板力与踏板行程的关系,设计控制器,提出基于神经元PID调节的控制策略,实现比传统制动系统更舒适的脚感,并保证安全性.
1 结构分析
传统制动系统是研究踏板行程模拟器的基础,通过分析并比较传统制动系统和线控制动系统,建立踏板行程模拟器模型,进行仿真分析,最后用台架试验进行验证.
1.1 传统车辆踏板力特性分析
带有真空助力器的制动系统如图1所示.

图1 传统制动系统实物图
通过台架试验可以得出踏板行程和踏板力以及踏板力和主缸压力之间的曲线关系.传统的真空助力制动系统的制动踏板力F与行程x的关系如图2所示[4-6].非作用冲程踏板行程与真空阀弹簧刚度和由阀的运动导致的行程距离有关.真空助力器的真空阀弹簧刚度和空气阀弹簧刚度严重影响制动踏板力和行程的特征.例如,真空阀弹簧刚度与非作用行程有关,当真空阀关闭之后产生踏板力.在非作用行程之后,真空阀关闭,踏板力开始增加,非作用行程之后的线性关系是由空气阀弹簧刚度影响的.这是因为真空阀关闭后产生踏板力,应用气室打开空气压力.当踏板释放时,踏板力减小,回位弹簧力引起踏板力迅速下降.应用阶段与释放非动作行程比较可以看出,当踏板释放时真空阀被很快打开,这是复位弹簧和电磁阀弹簧所起的作用.

图2 踏板力和踏板行程关系曲线
1.2 配有踏板行程模拟器的线控制动系统
采用的无真空助力器的线控制动系统如图3所示.

图3 无真空助力器的线控制动系统
此线控制动系统采用了制动踏板与制动液压回路非直接连接模式(除故障保护模式),为了获得驾驶员的制动意图以及保证驾驶员的良好制动感觉,需增设制动踏板行程模拟器,其结构如图3所示.为了确保制动的安全性,线控制动系统设计了故障保护模式.当线控制动系统正常工作时,截止阀关闭,如图4所示.

图4 线控制动正常模式
制动踏板施加力时,踏板力经主缸传给行程模拟器并产生反力,脚感由行程模拟器产生的反力引起,同时根据踏板连接处的角度传感器信号确定泵产生相应压力大小并传给轮缸实现车辆减速,而当线控制动系统有故障时,截止阀打开,如图5所示.

图5 线控制动故障保护模式
制动踏板施加力时,踏板力经主缸直接传给轮缸,脚感直接由轮缸产生,此时的脚感比较硬,如果加入液压助力之后,脚感会改善很多.
由上面的分析可得出踏板行程模拟器的2种工作状态,如图6所示,双位电磁阀为常闭状态,当系统正常工作时,双位电磁阀打开,油路通过模拟器,产生反力;电源一旦脱离或者出现故障,双位电磁阀闭合,油路直接通向轮缸,实现制动.

图6 踏板行程模拟器工作状态
1.3 线控制动系统动力学模型
在实际的制动过程中,踏板力与踏板行程和轮缸压力都随时间变化,因此需要建立踏板行程模拟器及相关部件的动力学模型,然后根据它们的动态特性决定其控制策略.
图3中的线控制动系统包括了多个机械结构,可建立行程模拟器、主缸和轮缸的力学模型.将踏板行程模拟器等效为一个单质量的弹簧阻尼系统,则活塞的运动微分方程为

式中:x为活塞的位移;A0为活塞的面积;m为液压缸活塞质量;c和k分别为踏板组件对活塞等效阻尼系数和等效刚度.
主缸活塞的力Fin平衡方程为

式中:p1为主缸压力;x1为主缸活塞位移;A1为主缸活塞面积;K1为主缸回位弹簧刚度.
轮缸活塞的力平衡方程为

式中:p2为轮缸压力;x2为轮缸活塞的位移;A2为轮缸活塞的面积;K2为轮缸回位弹簧刚度.
主缸活塞与轮缸活塞位移的关系为

从主缸流出的制动液流量为

式中:Cq为液压管路的有效流量系数.
踏板行程x和制动主缸位移x1的关系为

式中:L为制动踏板杠杆率.
忽略非线性库仑摩擦和孔的流量损失,并将式(3)-(6)代入式(2)得出施加在制动踏板的力为

用C1和C2替换式(7)中变量的系数,则制动踏板的力F简化为

根据台架试验通过imc数据采集系统测得数据(数据包括踏板行程x,踏板力F,踏板速度v),如表1所示,由以上数据采用最小二乘法估计出系统的系数 C1和 C2分别为3984.5和 -30.5.

表1 制动踏板动力学实测数据
综上所述,不具有真空助力器的踏板机构的踏板力是由踏板行程及其对时间的导数共同描述的.
基于上面的数学模型可以建立AMESim模型,该模型包括了制动踏板,主缸,踏板行程传感器,行程模拟器,电磁阀等等,并与Simulink建立联合仿真平台,控制阀的动作,模拟脚感,如图7所示.

图7 配有踏板行程模拟器的线控制动系统
2 控制策略
为了改善脚感的舒适度并实现踏板行程模拟器的精确动作,采用单神经元自适应智能PID控制器进行实时控制[7-8].单神经元自适应智能PID控制器(single neuron adaptive intelligent PID controller)不但结构简单,而且能够适应环境变化,有较强的鲁棒性.
控制器结构如图8所示,其中转换器的输入反映被控过程及控制设定的状态,设r(k)为设定值,y(k)为输出值,经转换器转换成为单神经元学习控制所需要得状态量 x1(k),x2(k),x3(k).x1(k)=e(k),x2(k)=e(k)-e(k-1),x3(k)=e(k)-2e(k-1)+e(k-2),ωi(k)为对应于xi(k)的加权系数;K为神经元的比例系数,K>0.神经元通过关联搜索来产生控制信号,即:


图8 单神经元自适应PID控制结构
单神经元自适应控制器是通过对加权系数的调整来实现自适应、自组织功能,权系数的调整是按有监督的Hebb学习规则实现的,它与神经元的输入、输出和输出偏差3者的相关函数有关,即:

为保证上述单神经元自适应PID控制器学习算法的收敛性和鲁棒性,对上述学习算法进行规范化处理后可得

式中:η为学习速率,η>0.
对于比例P、积分I和微分D分别采用了不同的学习速率ηP,ηI,ηD,以便对不同的权系数分别进行调整.K值的选择非常重要.K越大,则快速性越好,但超调量大,甚至可能使系统不稳定.当被控对象延时增大时,K值必须越小,以保证系统稳定.K值选择过小,会使系统的快速性变差.
在大量工程实际应用中,人们通过实践总结出P,I,D这3个参数的在线学习修正主要与e(k)和Δe(k)有关[9-10],基于此将上述单神经元自适应控制算法中的加权系数学习修正部分作些修改,即将ωi(k)中的xi(k)改为e(k)+Δe(k),改进后的算法变得更简单,计算速度和收敛速度也加快了,更好地满足实时控制的要求,使神经元控制能得到更广泛应用.改进后的算法如下:

采用上述改进算法后,加权系数的在线修正就不会是根据神经网络学习原理而是参考实际经验制定的.通过上述分析并针对其结构特点,利用Matlab/Simulink软件建立带有踏板行程模拟器的线控制动系统控制器模型,如图9所示,并与图7中的模型进行联合仿真.

图9 线控制动系统控制模型
3 仿真结果和试验数据分析
按典型工况进行制动,仿真曲线如图10所示,在前0.50 s之内进行正常制动,踏板力随时间增加,同时踏板行程也随着时间增加,0.50 s之后逐渐放开制动踏板,踏板力和踏板行程也随着时间减小,这个曲线特性符合传统制动要求.踏板力较踏板行程有时间延迟,克服间隙过程,这个特性符合传统制动系统的性能要求.

图10 踏板力和踏板行程分别与时间的关系
传统制动系统中,踏板力和踏板行程存在一定的关系,同样,在此制动系统中踏板力和踏板行程也存在这样的关系,如图11所示,与图2中的曲线有相似和区别之处.由于真空助力器中空气阀开启动作时间较长,故制动前段时间出现图2中的力延迟状态,如图2中a处;回位时由于空气阀回位弹簧作用,踏板力直线下降一段,如图2中b处.而在线性增长和下降的两段曲线和图2相似,随着踏板距离的增加,踏板力也相应的增加,相反也有相应回落曲线.在前0.02 s中,有一点波动,这种感觉可以忽略,相对图2中的传统制动系统来说,制动感觉平缓了很多,在制动前期,延迟也没传统制动系统明显,有效提高了制动的安全性能,尤其在紧急制动时体现更明显.
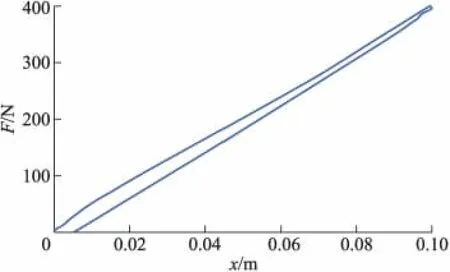
图11 踏板力与踏板行程特征曲线
图12为台架试验实测所得曲线,与仿真模型的仿真结果基本吻合,曲线变化趋势一致,达到了预期的效果.

图12 踏板力与踏板行程试验曲线
图13为摩擦片间隙x2与液压回路压力p3的关系曲线,带有踏板行程模拟器的线控制动系统的制动效果,在前半程随着踏板力的增加,液压回路中的压力随着时间增加,同时摩擦片与制动盘之间的距离逐渐减小,实现摩擦制动;相反,在松开制动踏板时,液压回路压力和摩擦片与制动盘之间的距离分别减小和增大.

图13 摩擦片间隙与液压回路压力关系
由上面的仿真曲线可以看出,该模型和控制策略能够实现传统制动系统的功能,并能提高舒适度.
4 结论
分析了传统制动系统和线控制动系统中制动踏板的特性,并通过试验得出相关特征曲线.随后利用AMESim和Simulink联合仿真技术构建了行程模拟器的虚拟仿真平台,在此基础上进行了典型工况的联合仿真验证.结果表明:该行程模拟器和控制策略能够达到传统制动系统的要求,并有效地改善了制动过程中的舒适度.整套系统具有很好的实时性,成本较传统制动系统低且能够满足实际应用的要求.
References)
[1]Ebert D G,Kaatz R A.Objective characterization of vehicle brake feel[C]∥ SAE Technical Paper Series.USA:SAE Publication Group,Paper Number:940311.
[2]Day A J,Ho H P,Hussain K,et al.Brake system simulation to predict brake pedal feel in a passenger car[C]∥SAE Technical Paper Series.USA:SAE Publication Group,Paper Number:2009-01-3043.
[3]郑宏宇,宗长富,高 越,等.线控制动系统的踏板力模拟研究[J].系统仿真学报,2008,20(4):1016-1019.Zheng Hongyu,Zong Changfu,Gao Yue,et al.Research on pedal force simulation for brake-by-wire system[J].Journal of System Simulation,2008,20(4):1016-1019.(in Chinese)
[4]宗长富,刘 凯.汽车线控驱动技术的发展[J].汽车技术,2006,22(3):1-5.Zong Changfu,Liu Kai.Development of the drive-bywire technology [J].Automobile Technology,2006,22(3):1-5.(in Chinese)
[5]Bill K,Semsch M,Breuer B.A new approach to investigate the vehicle iterface driver/brake pedal under real road condition in view of oncoming brake-by-wire-systems[C]∥SAE Technical Paper Series.USA:SAE Publication Group,Paper Number:1999-01-2949.
[6]Harsha A M,Abeykoon S,Ohnishi K.Implementation of pedal feeling for brake by wire system using bilateral control[C]∥Industrial Electronics,IEEE International Symposium.USA:IEEE,2008:1347-1352.
[7]何继爱,黄智武,田亚菲.一种单神经元PID控制器[J].甘肃科学学报,2004,16(4):70-73.He Jiai,Huang Zhiwu,Tian Yafei.A single neural PID controller[J].Journal of Gansu Sciences,2004,16(4):70-73.(in Chinese)
[8]玄圣夷,宋传学,靳立强,等.基于多级鲁棒PID控制的汽车稳定性控制策略[J].吉林大学学报:工学版,2010,40(1):13-18.Xuan Shengyi,Song Chuanxue,Jin Liqiang,et al.Multilevel robust PID control strategy for vehicle stability control[J].Journal of Jilin University:Engineering and Technology Edition,2010,40(1):13-18.(in Chinese)
[9]Ding Fang,Zhang Lili.Single neuron control based on genetic algorithm and its application[C]∥Computing,Control and Industrial Engineering.USA:IEEE,2011:74-77.
[10]Zheng Changlu,Fan Jian,Fei Minrui.PID neural network control research based on fuzzy neural network model[C]∥ Computational Intelligence and Software Engineering.USA:IEEE,2009:1-4.

