圆筒形超深海半潜式钻井储油平台运动特性分析

张永康，沈 翰，戴峰泽，倪 涛，庄建军

(1.东南大学机械工程学院，江苏 南京 211189;2.江苏大学机械工程学院，江苏 镇江 212013;3.南通中远船务工程有限公司，江苏 南通 226006)

据统计全球大于900 m水深的海域蕴藏着全球90%以上尚未开发的烃类资源，海洋油气总储量的44%蕴藏在大于2000 m的深水区［1］，因此，深水半潜式钻井平台将作为未来深水油气田开发的重要设备，深水半潜式钻井平台自产生以来经历了多次技术革新，现已是第6代，作业水深达3000 m，钻井深度达12000 m.根据国际上流行的浅海和深海的划分标准，水深小于500 m为浅海，大于500 m为深海，1500 m以上为超深海，第6代半潜式钻井平台达到了超深海的工作范围.目前第6代半潜式钻井平台多采用立柱稳定式结构，具有代表性的平台是GVA 7500平台，SEVAN 650平台是全球首座圆筒形结构的超深海半潜式钻井储油平台.

海洋平台在深水海域作业时受到海风、海浪和海流等多种海洋环境载荷作用，产生横摇、纵摇和垂荡等运动，剧烈的运动严重影响平台作业，甚至会造成平台倾覆，因此设计上就要求平台具有稳定的运动特性.国内外已有很多关于平台运动特性的研究，张威等［2］分别采用频域分析法与时域分析法对南海某立柱稳定式深水半潜式平台的运动响应进行计算，对比分析了2种方法在深水半潜式平台运动响应预报结果上的异同.S.Wu等［3］对立柱稳定式半潜式平台锚泊时受规则波作用的运动进行分析，得到了和模型试验结果一致的数值模拟结果.目前，立柱稳定式半潜式平台的运动特性已有较多研究，但未见有关圆筒形半潜式平台的研究文献.

半潜式平台运动特性的评估主要依据平台的运动响应幅值算子，平台的运动响应幅值算子越小，平台越稳定，J.A.van Santen等［4］推导出了近似计算半潜式平台运动的方程，B.J.Natvig等［5］用理论方法近似描述了规则波作用下海上结构物线性和非线性运动响应，但目前计算海洋平台的运动响应幅值算子多采用海工专业软件，如G.Clauss等［6］为研究水深对半潜式平台运动响应的影响，使用WAMIT软件对平台运动进行了模拟.M.A.Jordán等［7］为研究半潜式平台的运动响应，使用ANSYS软件的AQWA模块对平台的降阶模型进行计算分析.V.L.F.Matos等［8］使用WAMIT对深吃水半潜式平台二阶谐振运动进行了分析.ANSYS的AQWA模块主要用于结构流体动力学特征的评估及相关分析，它是世界3大船级社(美国船级社、英国劳氏船级社、挪威船级社)计算三维流体动力学的重要工具［9］.ANSYS Workbench将 ANSYS系列产品融合其中，与CAD系统的实体及曲面模型具有双向联结，可大幅降低除错时间，缩短设计与分析流程［10］.ANSYS软件AQWA模块的部分功能于ANSYS 12.0版本后进入ANSYS Workbench平台，并分解为Hydrodynamic Diffraction和Hydrodynamic Time Response的2个模块，其中Hydrodynamic Diffraction可用来计算海洋平台的运动响应幅值算子.

为研究圆筒形半潜式平台的运动特性，笔者使用Pro/E软件对SEVAN 650平台和GVA 7500平台建模，将模型导入ANSYS Workbench程序的Hydrodynamic Diffraction模块，计算出2座钻井平台风暴自存状态下的运动响应幅值算子，进而对比分析2座平台风暴自存状态下的运动特性.分析结论对圆筒形半潜式平台的设计和深海半潜式钻井平台的结构选型具有参考意义.

1 计算原理

实际作业时，半潜式海洋平台始终受随机波浪作用，为准确评价半潜式平台风暴自存状态下的运动特性，应考虑波浪的随机特性，需在线性假定下使用频域方法计算平台的运动响应.利用叠加原理，只要能知道在某一频域上，海洋平台运动对这一频率输入的运动响应，就可得到以波浪频率为自变量，海洋平台运动响应为变量的频率响应函数.为此首先要得到输入与输出间的关系，下面是海洋平台运动输入(波浪干扰力)和输出(海洋平台某一运动模态的运动)间的关系.海洋平台作为一个刚体，有6个运动自由度，其运动方程在频率域内可写为

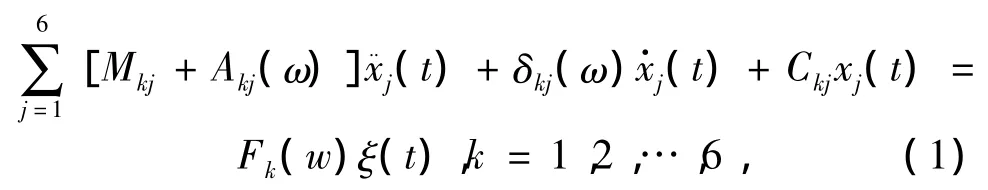
如果设海洋平台的运动x(t)与干扰波浪同为角频率ω的正弦振荡，则按照正弦运动的求导法则，有

将这些关系式代入式(1)中得

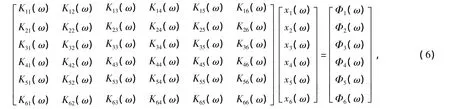
式(7)表示方程中矩阵的元素Kkj(ω)是由与海洋平台有关的质量系数Mkj、附加质量系数Akj(ω)及阻尼系数δkj(ω)等有关的参数组成的，它们均为角频率的函数;而波浪干扰力系数Fk(ω)则代表单位振幅的角频率为ω的规则波，在第k个运动模态内的干扰力(力矩)的幅值，所有量均为复数，代表角频率为 ω的振荡量的复数振幅.方程的解X=［x1x2x3x4x5x6］T为海洋平台的运动向量，可表示为

第k个运动模态的频率响应函数为

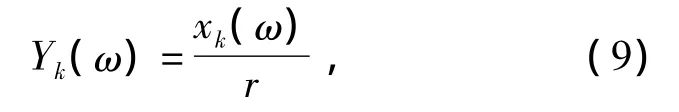
式中:r为波浪振幅，为单位高度，取为1.

频率响应函数的模为

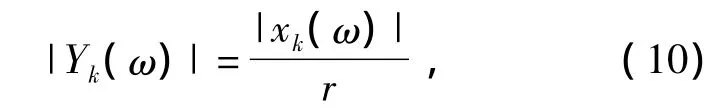
即运动振幅与波浪振幅的比值，将其作为海洋平台对应于角频率ω的运动响应幅值算子.

在频域理论的基础上，利用ANSYS Workbench的Hydrodynamic Diffraction模块模拟2座平台模型在随机波浪作用下的运动特性，可以得到各平台模型在相应波浪频率下的运动响应幅值算子函数曲线，通过对比分析，对平台的运动特性进行评价.

2 运动特性分析

SEVAN 650平台如图1所示，总体采用圆筒形构造，下部为双层底，内部建造有钻井、储油等功能模块，主体直径为85 m，主体高度为36.5 m，双层底直径为42 m，双层底高度为3.5 m，生存状态吃水为15 m，生存状态排水量为49143 t.GVA 7500平台如图2所示，在形式上采用了双下浮体、4立柱和箱型甲板结构，并使用大翼型横撑连接双下浮体，下立柱尺寸为108.80 m×16.00 m×10.24 m，立柱尺寸为16.80 m×14.40 m×23.76 m，双下浮体中心线距为62.08 m，生存状态吃水为19 m，生存状态排水量为47650 t.

图1 SEVAN 650平台

图2 GVA 7500平台

2座平台主要性能参数对比如表1所示，由于采用圆筒形结构形式，SEVAN 650平台与GVA 7500平台相比有着更大的存储能力和承载能力.

表1 SEVAN 650平台和GVA 7500平台主要性能参数对比

只考虑波浪载荷对平台的影响，故简化平台平均吃水线以上部分，用Pro/E软件对平台建模.建立右手坐标系，其中坐标系原点为各平台的底面和2竖直对称面的交点，x轴指向平台艏部为正，y轴指向平台左舷为正，z轴向上为正.半潜式平台有6个自由度，其运动形式分为2类:垂直面运动(垂荡、横摇、纵摇)和水平面运动(纵荡、横荡、艏摇)，根据所定义的坐标系，平台在Oxz平面上的摇摆为纵摇运动，平台在Oyz平面上的摇摆为横摇运动，平台在Oxy面上的摇摆为艏摇运动，平台沿z轴的上下振荡为垂荡运动，平台沿x轴前后振荡为纵荡运动，平台沿y轴左右振荡为横荡运动.半潜式平台垂向运动往往比较大，因此减小平台的垂向运动是半潜式平台设计中的一个重要方面，其中垂荡对半潜平台的垂向运动影响最大，但横摇和纵摇的影响也不可忽视［11］.因此，垂荡、横摇、纵摇这3种运动对平台风暴自存状态的运动特性影响最大，以下将对2种平台的3种运动响应幅值算子进行计算分析.

选择我国南海海况作为模拟参数，南海平均水深为 1212 m，波浪周期为 3.0 ～12.8 s［12］，其中周期为7.0～12.8 s的波浪对应着风暴情况下的海浪.使用ANSYS Workbench的Hydrodynamic Diffraction模块计算海洋平台运动响应幅值算子曲线的主要步骤:

1)在Pro/E软件中建立模型.

2)进入 ANSYS Workbench，将 Hydrodynamic Diffraction模块拖入Project Schematic中，编辑Geometry，将模型沿水线Slice分为上下2部分.

3)在模型中插入质量点，定义相关参数.

4)网格化模型，得到SEVAN 650有4048个节点，4048个单元，GVA 7500平台有2848个节点，2848个单元.

5)定义波浪方向的波浪范围为-180°至180°，插入的周期数为7，其中x轴方向波浪为艏浪，y轴方向波浪为横浪，其他方向为斜浪.定义波浪频率的类型为周期，范围从5 s到35 s，间隔周期为1 s.

6)在Solution中定义3项RAOs，对应于平台垂荡、横摇和纵摇的幅值响应，运算求解.

图3为2平台垂荡特性曲线.

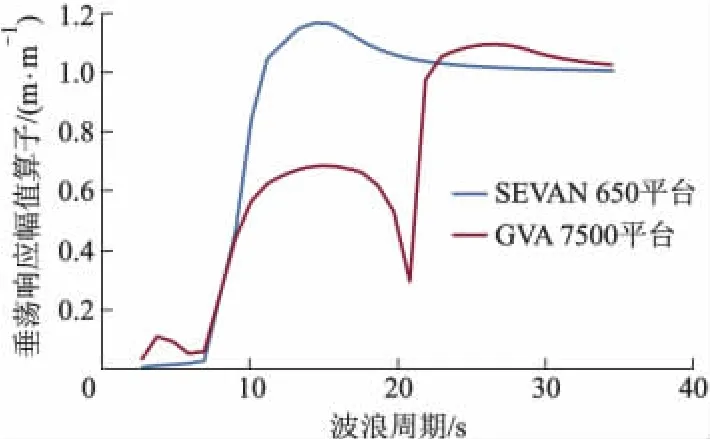
图3 垂荡特性曲线

从图3可以看出，波浪方向为斜浪，SEVAN 650平台垂荡响应固有周期为15 s，GVA 7500平台垂荡响应固有周期为26 s，两者均大于12.8 s，但GVA 7500的垂荡响应固有周期与SEVAN 650相比更加远离最大波浪周期，SEVAN 650平台的垂荡响应幅峰值大于GVA 7500平台.2平台在10 s时响应幅值大致相同，10 s之前SEVAN 650平台垂荡响应幅值小于GVA 7500平台，10 s之后SEVAN 650平台垂荡响应幅值大于GVA 7500平台.

图4为2平台横摇特性曲线，波浪方向为横浪，SEVAN 650平台横摇响应的固有周期为15 s，GVA 7500平台的横摇响应固有周期为11 s，SEVAN 650平台的横摇响应固有周期值在给定的波浪周期范围外，GVA 7500平台的横摇响应固有周期在给定波浪周期范围内，这会使GVA 7500平台发生共振，增加倾覆危险，GVA 7500的最大响应幅值低于SEVAN 650的值.在波浪周期为7.0～12.8 s的风暴情况下，SEVAN 650平台的横摇响应幅值小于GVA 7500平台.在7.0 s之前SEVAN 650平台的横摇响应幅值大于GVA 7500平台.

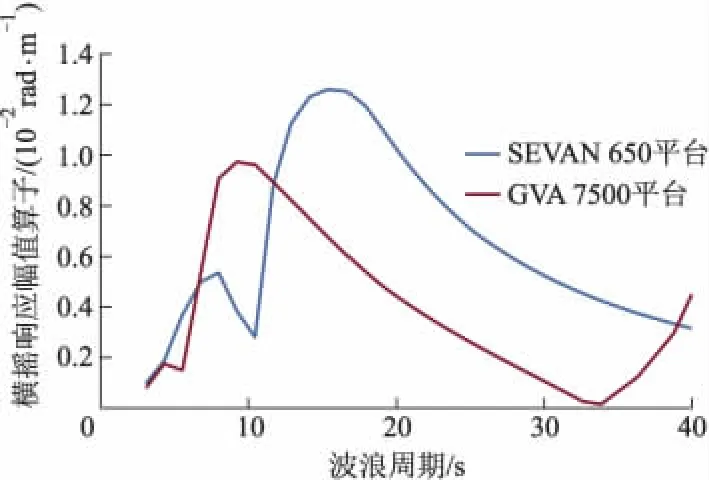
图4 横摇特性曲线

图5为2平台纵摇特性曲线.

图5 纵摇特性曲线

从图5可以看出，波浪方向为艏浪，SEVAN 650平台纵摇响应的固有周期为15 s，GVA 7500平台纵摇响应固有周期为11 s，SEVAN 650平台的纵摇响应固有周期值在给定波浪周期范围外，GVA 7500平台的纵摇响应固有周期在给定波浪周期范围内，这会使GVA 7500平台发生共振，增加倾覆危险，SEVAN 650平台的最大响应幅值大于GVA 7500平台最大响应幅值.在波浪周期为7.0～12.8 s的风暴情况下，SEVAN 650平台的纵摇响应幅值小于GVA 7500平台.在7.0 s之前SEVAN 650平台的纵摇响应幅值大于GVA 7500平台.

从图4，5可以看出，2平台的最大纵摇响应幅值均小于最大横摇响应幅值.综合图3-5的分析，可得表2结论.

表2 不同海况下2种平台运动响应幅值的比较

在风暴自存的情况下GVA 7500平台的垂荡性能比SEVAN 650平台稳定，而在正常作业海况下SEVAN 650平台比GVA 7500平台稳定.在风暴自存的情况下SEVAN 650平台的横摇和纵摇性能比GVA 7500平台稳定，而在正常作业海况下 GVA 7500平台比SEVAN 650平台稳定.

3 结论

垂荡对半潜式平台的作业稳定性影响最大，根据模拟结果，正常作业情况下适合选用SEVAN 650平台.横摇和纵摇性能不足易造成平台倾覆，根据模拟结果，风暴自存情况下适合选用SEVAN 650平台，且SEVAN 650平台比GVA 7500平台有更大的存储能力和承载能力.综合来看，在我国南海海况下，SEVAN 650圆筒形半潜式平台综合性能优于GVA 7500平台，但SEVAN 650平台在风暴情况下的垂荡响应幅值需要进一步减小.

References)

［1］杨 进，曹式敬.深水石油钻井技术现状及发展趋势［J］.石油钻采工艺，2008，30(2):10-13.Yang Jin，Cao Shijing.Current situation and developing trend of petroleum drilling technologies in deep water［J］.Oil Drilling ＆ Production Technology，2008，30(2):10-13.(in Chinese)

［2］张 威，冯 玮，谢 彬.深水半潜式平台运动响应预报方法的对比分析［J］.中国海上油气，2009，21(1):61-64.Zhang Wei，Feng Wei，Xie Bin.Comparative analysis on forecasting procedures of deepwater semi-submersible platform motion-response［J］.China Offshore Oil and Gas，2009，21(1):61-64.(in chinese)

［3］Wu S，Murray J J，Virk G S.The motions and internal forces of a moored semi-submersible in regular waves［J］.Ocean Engineering，1997，24(7):593-603.

［4］van Santen J A.Approximative formulae for calculating the motions of semi-submersibles［J］.Ocean Engineering，1985，12(3):235-252.

［5］Natvig B J，Pendered J W.Motion response of floating structures to regular waves［J］.Applied Ocean Research，1980，2(3):99-106.

［6］Clauss G，Stempinski F，Dudek M，et al.Water depth influence on wave-structure-interaction［J］.Ocean Engineering，2009，36(17/18):1396-1403.

［7］Jordán M A，Beltrán-Aguedo R.Optimal identification of potential-radiation hydrodynamics for moored floating structures:a new general approach in state space［J］.O-cean Engineering，2005，31(14/15):1859-1914.

［8］Matos V L F，Simos A N，Sphaier S H.Second-order resonant heave，roll and pitch motions of a deep-draft semi-submersible:theoretical and experimental results［J］.Ocean Engineering，2011，38(17/18):2227-2243.

［9］邓文彬.船舶与海洋工程产品设计的领航员AQWA＆ASAS［J］.中国制造业信息化，2006(16):58-59.Deng Wenbin.Shipping and marine engineering product design navigator AQWA ＆ ASAS［J］.Manufacture Information Engineering of China，2006(16):58-59.(in Chinese)

［10］王宝贵，张以都.斜齿轮的参数化建模及接触有限元分析［J］.装备制造技术，2007(12):37-38.Wang Baogui，Zhang Yidu.Parametric modeling of helical gear and contact analysis with FEA［J］.Equipment Manufacturing Technology，2007(12):37-38.(in Chinese)

［11］曾 志.半潜式平台气隙响应的预报［D］.上海:上海交通大学船舶海洋与建筑工程学院，2009.

［12］孙东昌，潘 斌.海洋自升式移动平台设计与研究［M］.上海:上海交通大学出版社，2008.