基于CFD的离心泵侧壁式压水室优化设计
杨敏官,张 宁,李 忠,高 波
(江苏大学能源与动力工程学院,江苏 镇江 212013)
离心泵作为一种通用机械在工业输送、城市生活和农业排灌等领域发挥着巨大的作用,同时也消耗了大量的能源.离心泵的振动一直是人们关注的焦点问题[1-3],振动严重时甚至能损坏设备[4].在某些特殊领域对离心泵的振动性能有严格的要求,有时甚至会牺牲泵的效率来获得较低的振动水平,如何降低离心泵的振动一直困扰着工程技术人员.压力脉动是引起泵振动的主要因素之一[5],由于侧壁式压水室改变了隔舌相对叶轮的位置,可以有效地减小叶轮和隔舌间的动静干涉作用,因此采用侧壁式压水室可以有效地改善离心泵的振动性能,目前有关侧壁式压水室的研究还未见相关的文献报道,因此对侧壁式压水室进行研究优化,从而获得较高的效率和较低的压力脉动水平对工程应用有实际指导意义.
流体机械内部流动是一种复杂的三维湍流运动,对其进行研究面临着许多困难,近年来随着计算机技术和湍流理论的发展以及大型CFD软件的成功开发使得流体机械内部数值模拟成为可能[6-8].笔者采用Fluent软件对比转数为130的侧壁式压水室离心泵内部流动进行数值模拟,通过研究侧壁倾斜角及叶轮外径和压水室基圆直径之间的间隙来获得离心泵较高的效率和低的压力脉动水平.
1 侧壁式压水室离心泵基本结构参数
泵的性能参数:流量为48 m3·h-1;扬程为7.8 m;转速为1450 r·min-1;比转数为130;叶轮进口直径为100 mm;叶轮外径D2为172 mm;叶片数为6.
压水室可以有效地消除液体的旋转,和叶轮的匹配关系对泵的效率及振动水平有重要的影响.针对侧壁式压水室特殊的结构形式,目前只考虑2个重要变量:基圆直径D3和侧壁倾斜角,其他参数则按照常规方法来设计计算.根据设计要求D3取如下值:175,185,195,205,215,225,235,245 mm,侧壁倾斜角 θ取如下值:10°,15°,20°,25°.压水室其他参数:扩散管的扩散角为 9°;扩散管高度为238 mm;压水室进口宽度为35 mm.
侧壁倾斜角θ的定义如图1所示.
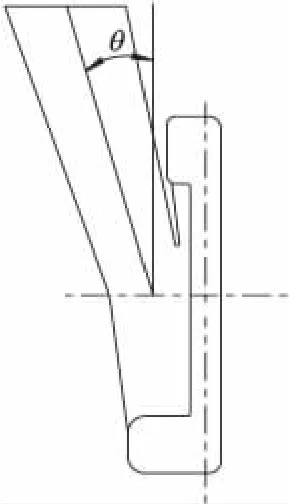
图1 侧壁式压水室二维图

2 数值计算方法
2.1 网格及计算区域划分
根据离心泵的流动特性将流动区域划分为3个区:静止区1为进口流道,静止区2为侧壁式压水室,旋转区为叶轮.以D3=205 mm,θ=15°的侧壁式压水室离心泵为例在Gambit中进行网格划分,并采用2种网格检验数对网格进行无关性检查.在确保网格的计算精度和计算结果准确性的基础上,采用非结构化四面体单元对计算区域进行网格划分,叶片表面采用了加密处理,网格数如下:进口流道的网格数为182679,侧壁式压水室网格数为589657,叶轮网格数为653540.叶轮及压水室网格如图2所示.

图2 叶轮及侧壁式压水室网格
2.2 控制方程
当流体不可压缩时,连续性方程为
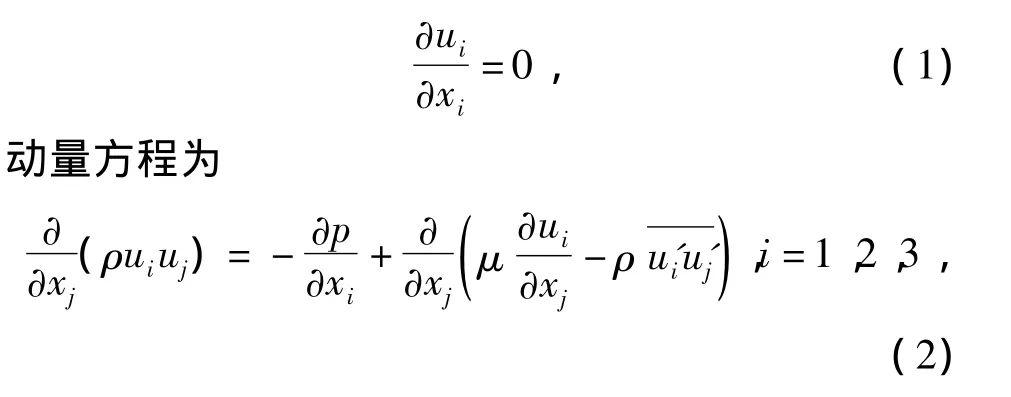
式中:ρ为液体密度;ui为i方向的雷诺平均速度;p为平均静压;u'i为脉动量.
标准k-ε方程为

式中:μt为湍动黏度;Gk为湍动能生成项;C1ε=1.44;C2ε=1.92;Cμ=0.09;σε=1.3;σk=1.0.
2.3 计算方法及边界条件
固体壁面采用无滑移条件,近壁区域采用标准壁面函数处理.采用一阶迎风格式对速度、湍动能和湍动能耗散率进行离散.采用SIMPLE算法实现速度和压力之间的耦合.在计算域的进口断面采用绝对速度进口,进口无预旋,并且在进口给定k-ε的数值,该值由下式确定:
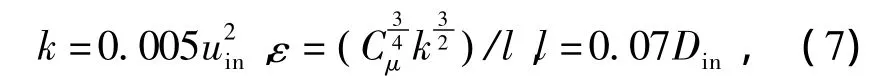
式中:uin为进口轴向速度;l为进口处湍流特征长度.
在计算域的出口(即蜗壳出口)面采用自由出流边界条件.亚松弛因子均采用Fluent软件的默认值.
3 计算结果及分析
3.1 能量性能分析
3.1.1 水力效率
λ 分别为 0.017,0.076,0.134,0.192,θ=15°时,侧壁式压水室离心泵的水力效率曲线ηh,如图3所示,泵的最高效率点偏向大流量工况,位于1.2Qd(Qd为规定流量)附近,最高水力效率为82%左右.而比转数为130的常规螺旋型蜗壳离心泵最高水力效率约为90%,两者相差8%.

图3 水力效率曲线
图4为压水室断面上速度流线图.

图4 压水室断面流线图
由于压水室结构的变化,在流体流经侧壁式压水室的过程中,过流断面上出现旋涡,且随流动轴向扩散加剧,断面上大尺度旋涡强度减弱,导致一部分能量的损耗,这是造成侧壁式压水室离心泵的水力效率比常规压水室偏低的重要原因,因此侧壁式压水室结构只适用于对振动有特殊要求的领域.
图5为在规定流量下,不同侧壁倾斜角及间隙率时离心泵的水力效率变化曲线.在侧壁倾斜角不变时,随着间隙率的增大,泵的水力效率增大,并在λ=0.308时取得最大值.当间隙率不变,随着侧壁倾斜角增大泵的水力效率先增大后减小,并在侧壁倾斜角为15°时取得最大值.但当侧壁式压水室的间隙率过大时会造成泵的径向尺寸增大,增加泵的制造成本,间隙率大于0.192时,效率增加的幅值明显减弱,考虑径向尺寸和效率,间隙率的上限为0.192.
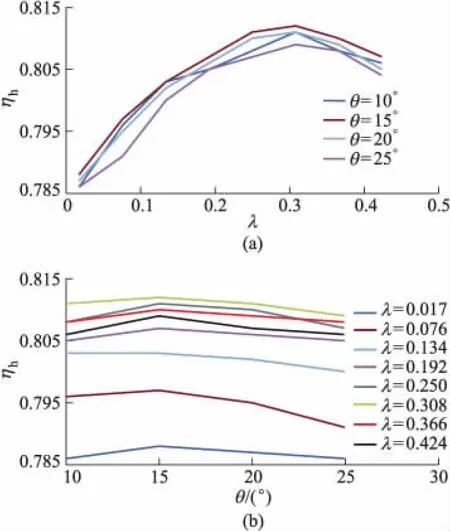
图5 不同间隙率和倾斜角时泵的水力效率
3.1.2 扬 程
在规定流量下泵扬程H随不同侧壁倾斜角θ及间隙率λ的变化情况,如图6所示.

图6 扬程变化曲线
随着间隙率的增加扬程略有上升,整体变化趋势和水力效率相近,在λ=0.308时取得最大值.由于数值计算没有考虑泵的机械损失和容积损失,因此扬程略高于设计值.但不管间隙率及倾斜角如何改变,泵的扬程变化幅值都很小,最大差值为0.11 m,相对变化率为1.4%,因此可以认为侧壁倾斜角及间隙率对泵的扬程几乎没有影响.
3.1.3 轴功率
图7为轴功率P随间隙率及倾斜角的变化情况,在间隙率较小时轴功率较大,随着间隙率的增加轴功率快速下降,之后基本保持不变,在不同倾斜角时轴功率变化不大.随着间隙率及倾斜角的改变,泵的效率和轴功率变化明显而扬程基本保持不变,综合考虑泵的径向尺寸和性能,间隙率的上限取值为0.192,倾斜角为 15°.

图7 轴功率变化曲线
3.2 压力脉动特性分析
在流量为 0.8Qd,1.0Qd,1.2Qd下,对侧壁式压水室离心泵在D3=205 mm,4种不同倾斜角下,进行压力脉动监测.泵转速为1450 r·min-1,设置时间步长为1.15 ×10-4s,周期 T=0.0414 s监测点的位置如图8所示.

图8 监测点位置
图9为规定流量下压力脉动随时间变化曲线.在一个周期内(T=0.0414 s)会出现6个波峰和波谷.由于所采用的叶轮叶片数为6,该现象是由叶轮和隔舌间的动静干涉作用引起的.
将时域信号快速傅立叶变换(FFT)为频域信号,如图10所示.泵的转速为1450 r·min-1,故轴频为24.2 Hz,叶频f1为145 Hz,脉动峰值信号出现在叶频及其高次谐波处,在叶频处压力脉动的幅值p1最大,即叶频在由压力脉动引起的泵振动中占主导作用.

图9 压力脉动随时间变化情况

图10 压力脉动频域图
在叶频处压力脉动幅值随侧壁倾斜角的变化情况,如图11所示.

图11 叶频处脉动幅值
由于泵的最高效率点偏向大流量(1.2Qd)工况,因此当偏离最优工况时泵的压力脉动幅值增加.在3种流量下随着侧壁倾斜角的增加,叶频处脉动幅值都呈先减小后增加的趋势,并在倾斜角为15°时取得最小值,说明当倾斜角取15°时泵的振动水平会明显下降.同时泵的水力效率也达最大值.图12为在倾斜角为15°,6种不同间隙率时,离心泵压力脉动频域图及叶频和高次谐波幅值随间隙率变化情况.

图12 不同间隙率时压力脉动变化图
从图12a可以看出,在间隙率较小时压力脉动信号中存在大量的高频成分,且压力脉动幅值较高,而当间隙率增加时高频成分减弱.从图12b可以看出,不管叶频还是其高次谐波的幅值都随间隙率的增加呈下降趋势,这是因为当间隙率增加时,叶轮和隔舌间的动静干涉作用减弱,从而使脉动水平呈现明显的下降,但当λ大于0.192时,压力脉动幅值下降趋势变缓.增加间隙率可以有效地降低压力脉动幅值,但综合考虑效率、压力脉动、压水室的径向尺寸,建议间隙率合理取值范围为0.134~0.192.
4 结论
采用侧壁式压水室的离心泵,水力效率和常规螺旋型蜗壳离心泵相比明显下降,且高效点偏向大流量工况.表明:为了获得较低的振动水平,侧壁式压水室离心泵牺牲了较大的水力效率,通常只在某些对振动有特殊要求的领域才考虑采用侧壁式压水室.随着侧壁式压水室间隙率及倾斜角的变化,泵的水力效率先增加后减小,并在θ=15°,λ=0.308时取得最大值.间隙率不变,叶频处的脉动幅值在倾斜角为15°时取得最小值,随着间隙率的增加泵的压力脉动幅值水平呈下降趋势.对于侧壁式压水室,综合考虑泵的效率、压力脉动和压水室的径向尺寸,间隙率合理取值范围为0.134~0.192,侧壁倾斜角为15°.
References)
[1]Friedrichs J,Kosyna G.Rotating cavitation in a centrifugal pump impeller of low specific speed [J].Journal of Fluids Engineering,2002,124:356-361.
[2]Spence R,Amaral-Teixeira J.Investigation into pressure pulsations in a centrifugal pump using numerical methods supported by industrial tests[J].Computers & Fluids,2008,37:690-704.
[3]Barrio R,Parrondo J,Blanco E.Numerical analysis of the unsteady flow in the near-tongue region in a volutetype centrifugal pump for different operating points[J].Computers & Fluids,2010,39:859-870.
[4]Duplaa S,Coutier-Delgosha O,Dazin A,et al.Experimental study of a cavitating centrifugal pump during fast startups[J].Journal of Fluid Engineering,2010,132(2):021301-1-12.
[5]袁建平,付燕霞,刘 阳,等.基于大涡模拟的离心泵蜗壳内压力脉动特性分析[J].排灌机械工程学报,2010,28(4):310-314.Yuan Jianping,Fu Yanxia,Liu Yang,et al.Analysis on pressure fluctuation within volute of centrifugal pump based on large eddy simulation[J].Journal of Drainage and Irrigation Machinery Engineering,2010,28(4):310-314.(in Chinese)
[6]Spence R,Amaral-Teixeira J.A CFD parametric study of geometrical variations on the pressure pulsations and performance characteristics of a centrifugal pump[J].Computers & Fluids,2009,38:1243-1257.
[7]Moscato F,Colacino F M,Arabia M,et al.Pressure pulsation in roller pumps:a validated lumped parameter model[J].Medical Engineering & Physics,2008,30:1149-1158.
[8]Lucius A,Brenner G.Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation[J].International Journal of Heat and Fluid Flow,2010,31:1113-1118.

