两个半离散逆向的Hilbert型不等式
巫伟亮
(嘉应学院数学学院,广东梅州514031)
1908年德国数学家D.Hilbert创立了经典离散的Hilbert不等式:若0<Σ∞,则
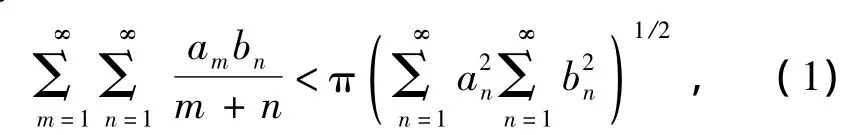
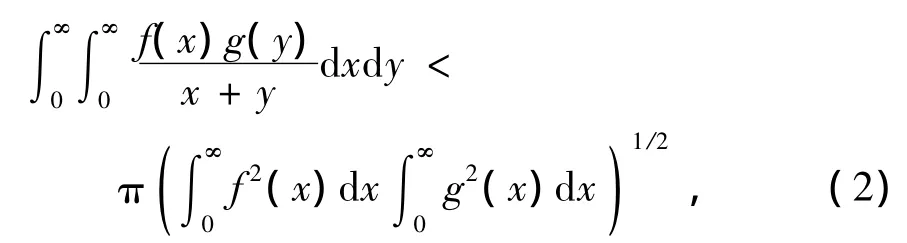
这里,常数因子π为最佳值.式(1)、(2)是分析学的重要不等式[1-2].最近,文献[3]-[10]通过估算权函数及运用参量化的思想对半离散Hilbert型不等式进行了研究.
本文应用估算权系数的方法及实分析的思想,分别从0<p<1及p<0两种情况建立了新的含有核为A<1)、半离散逆向的Hilbert型不等式,证明了其常数因子为最佳值并考虑了它们的等价式.
1 若干引理
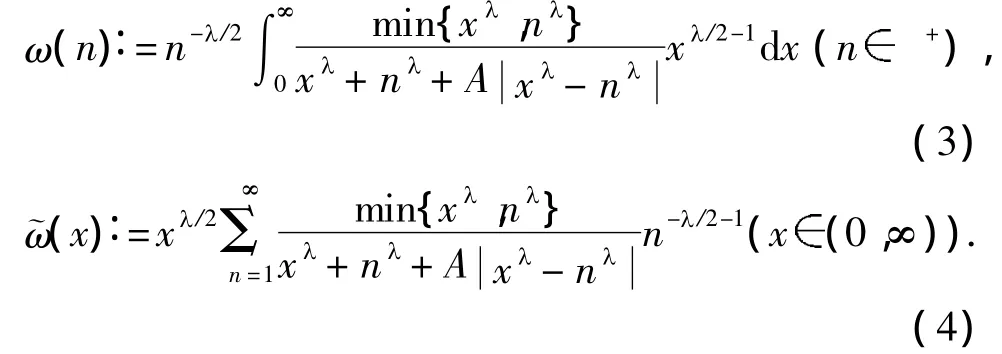
则有
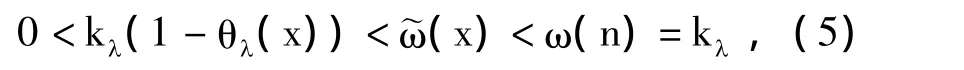
这里,

证明 在式(3)中作变换u=(x/n)λ/2,查积分表可得
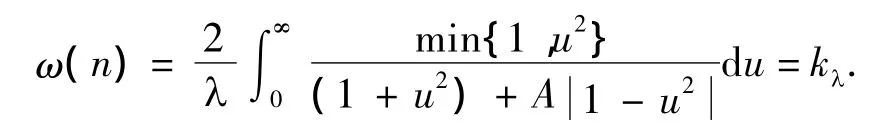
因0<λ≤2,对于固定的x>0,函数
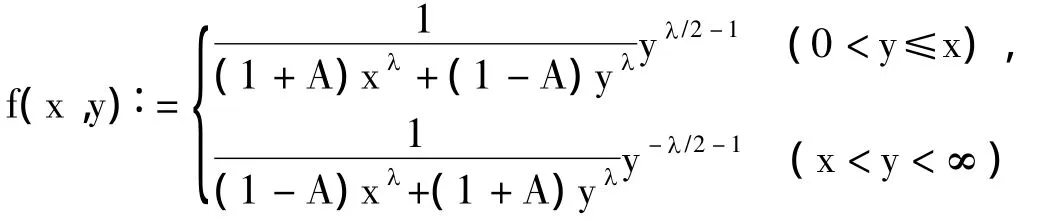

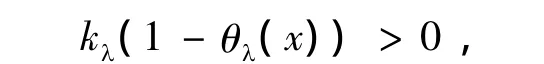
这里,θλ(x)=
事实上,当0<x<1时,
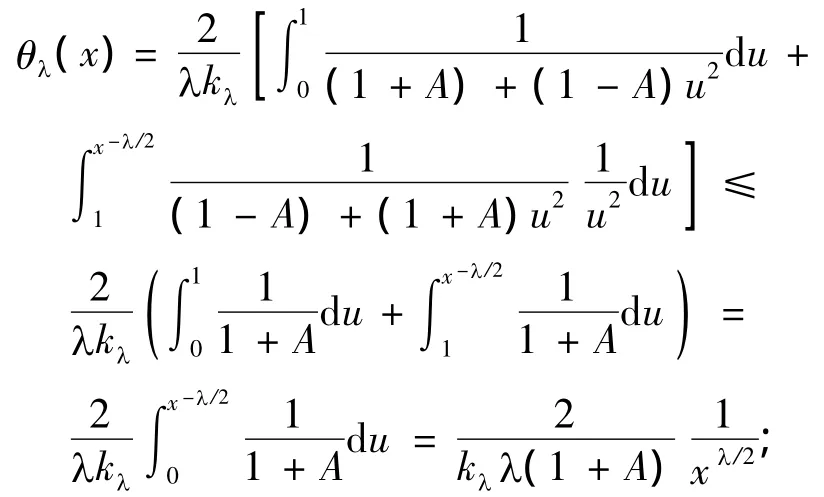
当x≥1时,

式(5)成立.证毕.
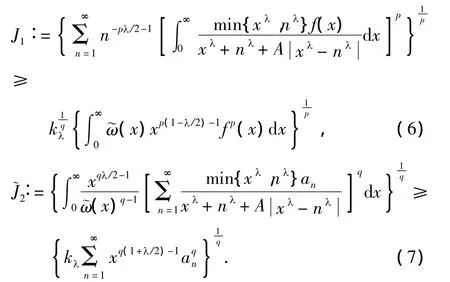
证明 当0<p<1时,设

一方面,由逆向的Hölder不等式[11]及式(3)~(5),有
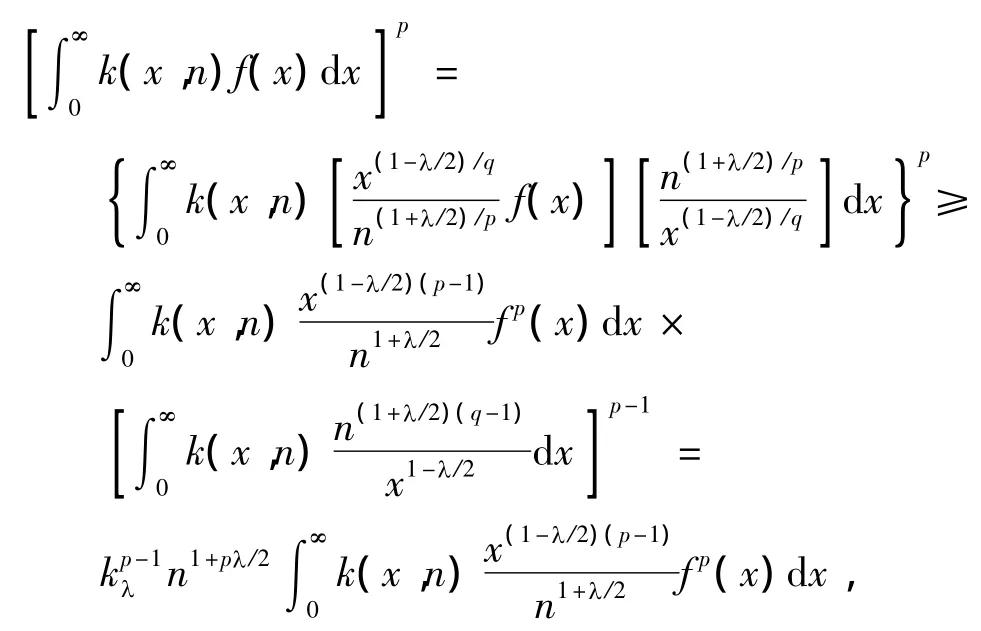
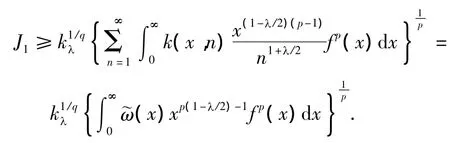
故式(6)成立.另一方面,同理可得
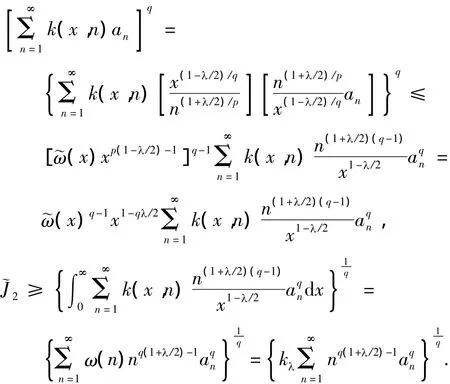
故有式(7).类似地,当p<0时,运用Hölder不等式及式(5),式(6)和式(7)仍成立.证毕.
2 主要结果
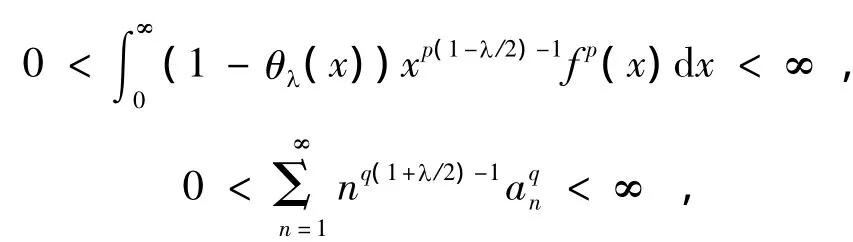
则有如下等价的不等式:
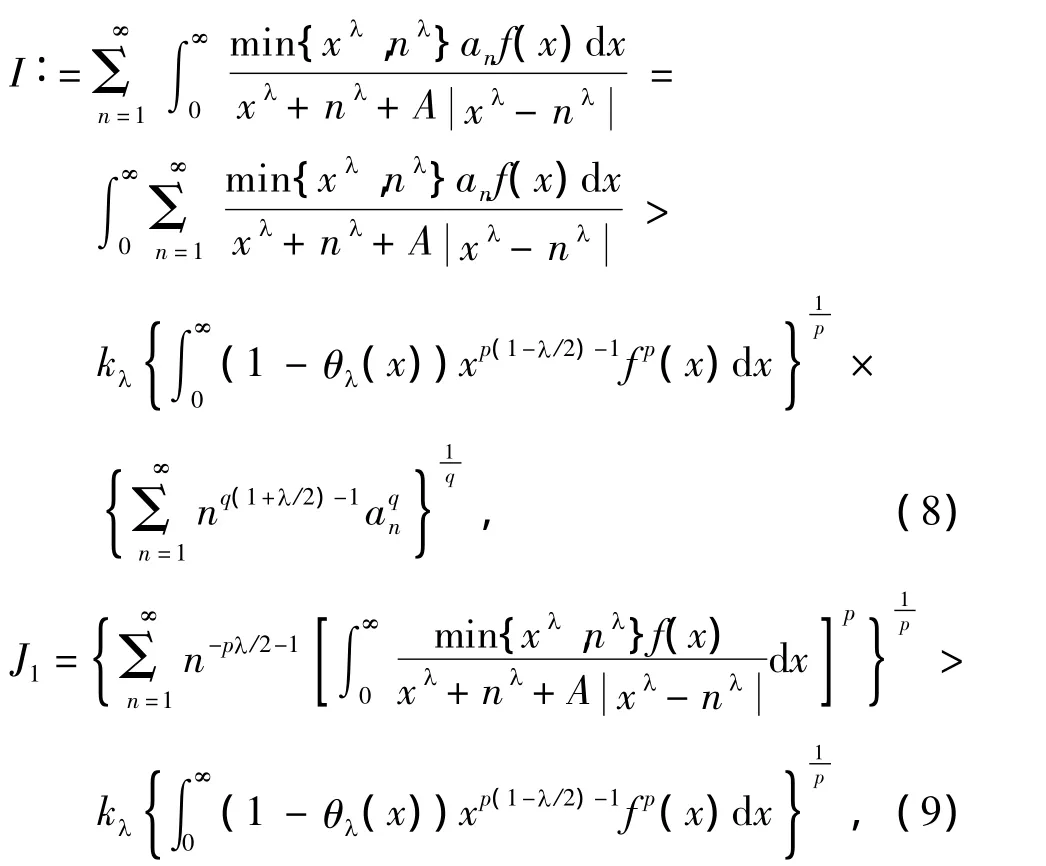
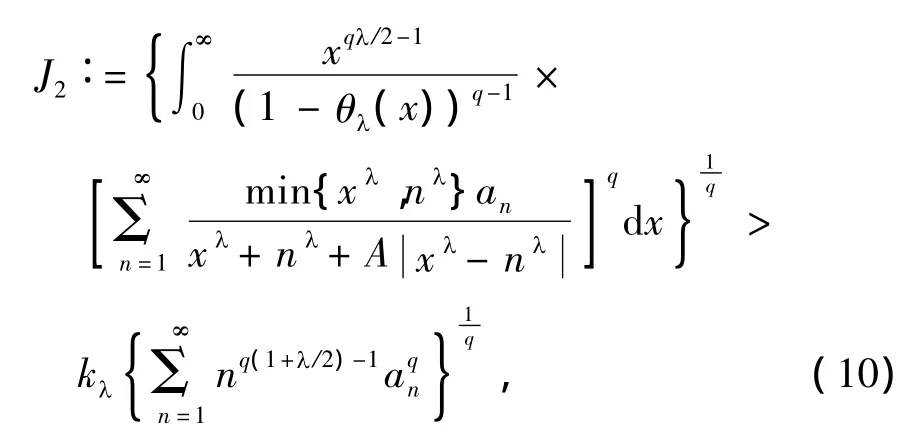
这里,常数因子kλ是最佳值.
证明 由 L逐项积分定理[12],式(8)中 I有2种表示.由条件,式(6)取严格不等号,式(9)成立.由逆向的 Hölder不等式[11],有
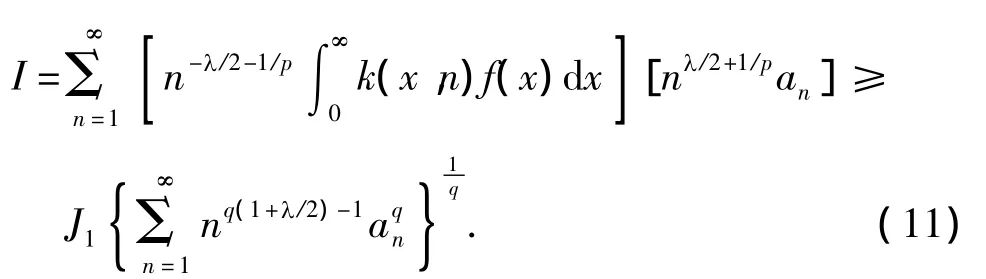
由式(9),有式(8).反之,设式(8)成立.取

运用式(8)得
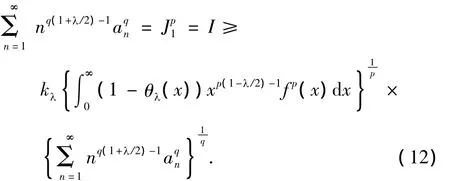
由式(6)及条件,知 J1>0.若 J1=∞,则式(9)显然成立;若J1<∞,则式(8)严格不等号成立的条件都具备,式(12)取严格不等号,且有
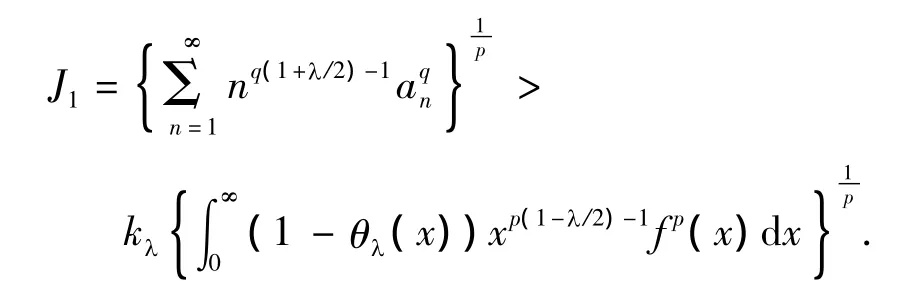
有式(9)与式(8)等价.由条件及式(7),有式(10).根据逆向的Hölder不等式,一方面
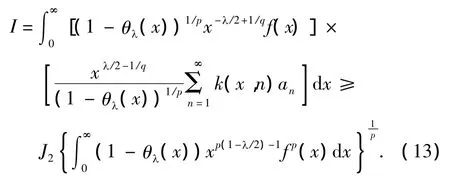
由式(10),式(8)成立.另一方面,设式(8)成立.取

由式(8)有
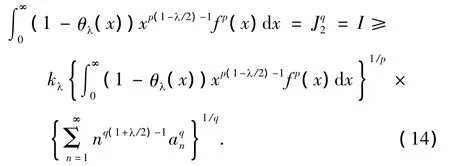
由式(7)及条件,知J2>0.若J2=∞,则式(10)显然成立;若J2<∞,应用式(8),式(14)取严格不等号,且有

故有式(10)与式(8)等价.综上可导出式(8)、式(9)与式(10)齐等价.

事实上,可求得
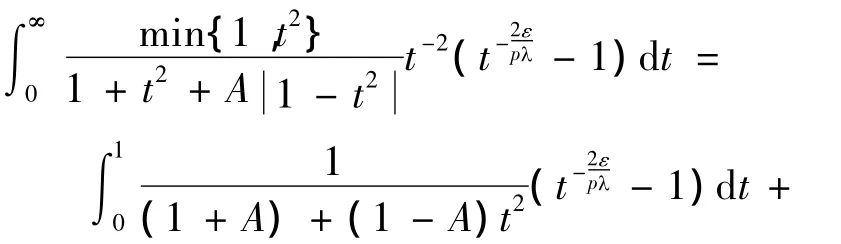

由式(15)、(16),有
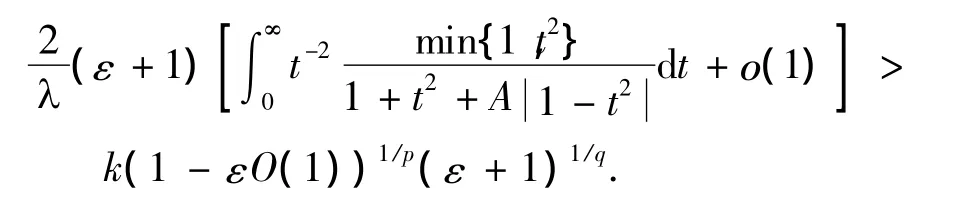
故有 k≥kλ(ε→0+).因而 k=kλ为式(8)的最佳值.式(9)及式(10)的常数因子也必为最佳值.若不然,由式(11)、(13),必可推导出式(8)中的常数因子kλ不为最佳值的矛盾.证毕.
当p<0时,由引理2及类似定理1的证明,可得:
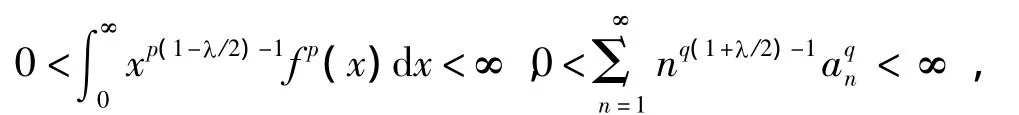
则有如下的等价的不等式:
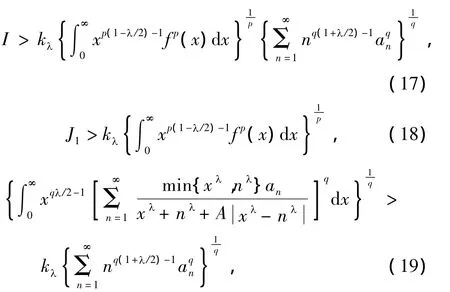
这里,常数因子kλ具有最佳性.
致谢 衷心感谢杨必成教授的耐心指导与帮助!
[1]HARDY GH,LITTLEWOOD JE,POLYAG.Inequalities[M].Cambridge:Cambridge University Press,1952.
[2]MINTRINOVICE D S,PECARIC J E,FINK A M.Inequalities involving functions and their integrals and derivatives[M].Boston:Kluwer Academic Publishers,1991.
[3]KRNIC M,PECARIC J.Hilbert's inequalities and their reverses[J].Publ Math Debrecen,2005,67(3-4):315-331.
[4]AZAR L.On some extensions of Hardy-Hilbert’s inequality and applications[J].J Inequal Appl,doi:10.1155/2008/546829.
[5]杨必成.一个半离散非齐次核的Hilbert不等式[J].湛江师范学院学报,2011,32(3):5-9.
[6]杨必成.关于一个半离散的Hilbert型不等式[J].汕头大学学报:自然科学版,2011,26(4):5-10.
[7]杨必成.一个半离散且非齐次核逆向的Hilbert不等式[J].湖南理工学院学报:自然科学版,2011,24(3):1-4.
[8]杨必成.关于一个半离散且非齐次核逆向的Hilbert不等式[J].内蒙古大学学报:自然科学版,2011,40(5):433-436.
[9]YANG Bicheng.A mixed Hilbert-type inequality with a best constant factor[J].Int JPure Appl Math,2005,20(3):319-328.
[10]杨必成.一个半离散的Hilbert不等式[J].广东第二师范学院学报,2011,31(3):1-7.
[11]匡继昌.常用不等式[M].济南:山东科技出版社,2004.
[12]匡继昌.实分析引论[M].长沙:湖南教育出版社,1996.

