单圈图的最小无号Laplacian谱展

游志福

(广东技术师范学院计算机科学学院，广东广州510665)

设G为n阶简单图，其顶点集V(G)={v1，v2，…，vn}．对于点u，用N(u)表示u的邻点集，d(u)是点u的度．图G的最大度和最小度分别用Δ和δ表示．设G-v是由G通过删去点v和关联v的所有边所成的图．图G的邻接矩阵，记为A(G)=(aij)n×n，是n阶方阵，其中当顶点 vi和vj在G中相邻时aij=1，否则aij=0．矩阵A(G)的特征多项式也称为图G的特征多项式:

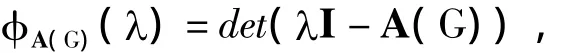
其中I为n阶单位阵．由于A(G)是实对称矩阵，所以其n个特征值都是实数，记为λ1(G)，λ2(G)，…，λn(G)，在不引起混淆的情况下简记为 λ1，λ2，…，λn．不失一般性设 λ1≥λ2≥… ≥λn，并称它们为图G的特征值．G的特征值的全体称为图G的谱．

图的度矩阵 D=diag(d1，d2，…，dn)是图 G 的由点度构成的对角矩阵．图G的Laplacian矩阵定义为L(G)=D(G)-A(G)．矩阵L(G)的特征多项式也称为图G的Laplacian特征多项式:

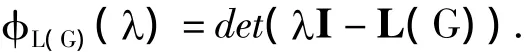
矩阵L是实对称、半正定的奇异矩阵，记其特征值为 μ1≥μ2≥…≥μn-1≥μn=0．

图 G 的谱展［1］定义为:S(G)=λ1- λn．图 G 的Laplacian 谱展［2］定义为:LS(G)=μ1-μn-1．

矩阵Q(G)=D(G)+A(G)称为无号Laplacian矩阵，其特征多项式也称为图G的无号Laplacian特征多项式:

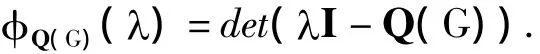
设其特征值为q1≥q2≥…≥qn-1≥qn≥0．

类似于邻接和 Laplacian谱展，图 G的无号Laplacian 谱展［3-4］定义为 QS(G)=q1-qn．

OLIVEIRA等［4］给出:Pn在 n阶树图中取得最小无号Laplacian谱展．本文刻画了给定阶数的连通单圈图无号Laplacian谱展的下界及极图．

简记无号Laplacian矩阵的特征值为Q-特征值．引理1说明了图G的去边子图的Q-特征值内插图G的Q-特征值．

引理1［5］设 e 是图 G 的一条边，q1，q2，…，qn(q1≥…≥qn)和 s1，s2，…，sn(s1≥…≥sn)分别是 G和G-e的Q-特征值，则

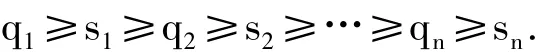
引理2 设G是一个n阶图且v是一个悬挂点，则 QS(G)≥QS(G-v)．

证明 对于悬挂点v，设G和G-v的Q-特征值分别为q1≥…≥qn和s1≥…≥sn-1．注意到s1，…，sn-1和sn=0是 G-e的 Q-特征值，其中 e是关联点v的边．由引理1，有

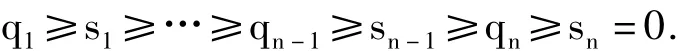
从而 QS(G)=q1-qn≥s1-sn-1=QS(G-v)． □

引理3［6-7］设G是一个至少有一边的图，则q1≥μ1≥Δ+1．若G是连通的，第1个等号成立当且仅当G是二部图，第2个等号成立当且仅当Δ =n-1．

Ea，b表示通过合并圈Ca中的一顶点和Pb+1的一个端点所成的a+b阶单圈图．文献［5］指出

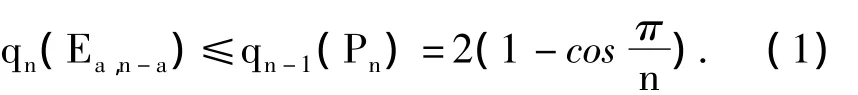
根据文献［8］中一个关于最大Laplacian特征值的下界，YOU 和 LIU［9］获得了:

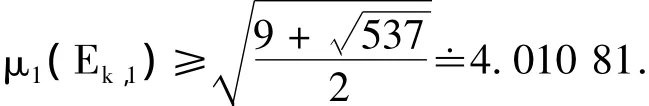
下面引理对本文主要结果有重要意义，其中Ea，b如上所定义．

引理4 设k≥3是一个任意正整数，则

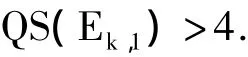
证明 对于k≥30，由式(1)和引理3，有

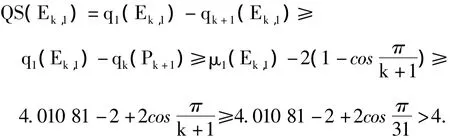
当3≤k≤29，由直接计算可得表1．

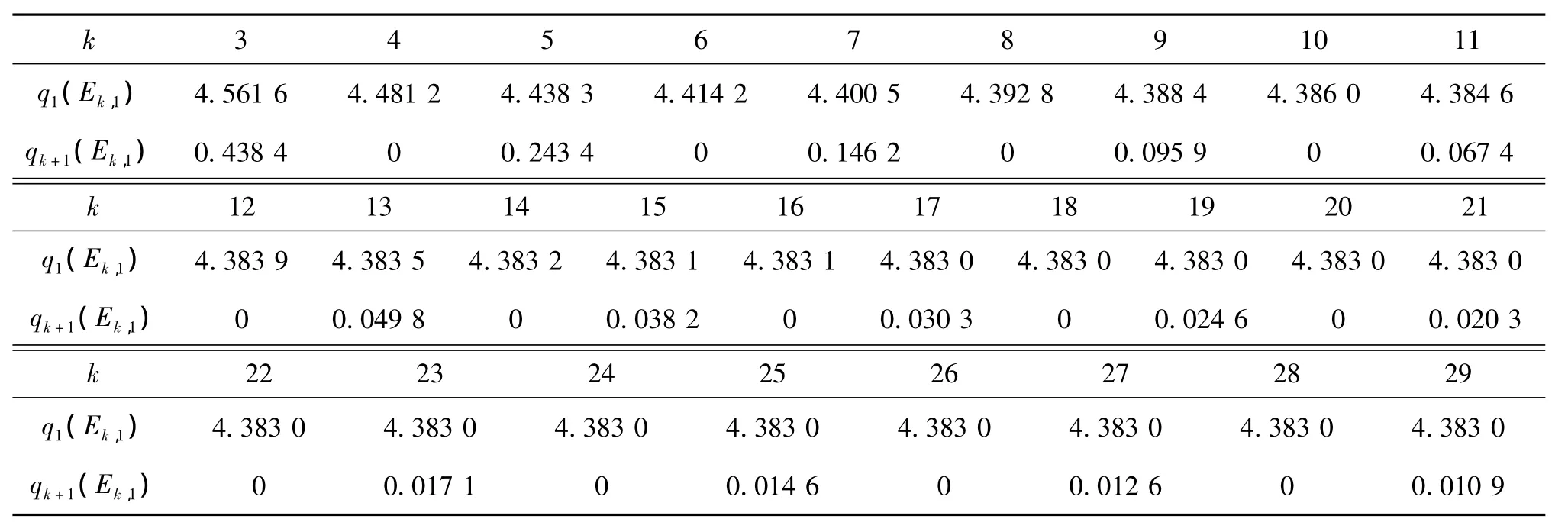
表1 Ek，1(3≤k≤29)的最大和最小无号Laplacian特征值Table 1 The largest and smallest signless Laplacian eigenvalues of Ek，1(3≤k≤29)

如果3≤k≤29，由表1，有 QS(Ek，1)＞4．综上可知结论成立．

引理5［3］如果G是一个连通图且最大度为Δ，最小度为 δ，则QS(G)＞Δ +1-δ．

定理1 设G是一个n阶单圈图且G≇Cn，则QS(G)＞4．

证明 注意到 G≇Cn，则 δ=1．若 Δ≥4，由引理5，有 QS(G)＞4+1-1=4．

下设G是一个n阶单圈图且Δ=3．令v是一个悬挂点．由引理2，有QS(G)≥QS(G-v)．若G-v≅Cn-1，即 G≅En-1，1，由引理 4，有 QS(G)＞ 4．若 G≇En-1，1，通过逐渐删去图G的悬挂点，则G可以转化为 Ek，1(k≤n-2)且

因此，定理1的结论成立． □

引理6［10］设 q1是连通图 G的最大 Q-特征值，则q1=4当且仅当G是一个圈或者K1，3．

引理7［10］连通图的最小无号Laplacian特征值等于0当且仅当此图是二部图．

由引理6和引理7，有:

命题1 设Cn是n阶圈图，则QS(Cn)≤4且等号成立当且仅当n是偶数．

结合定理1和命题1，有:

定理2 设G是一个n阶单圈图，则QS(G)≥QS(Cn)．等号成立当且仅当G≅Cn．

［1］GREGORY D A，HERSHKOWITZ D，KIRKLAND S J．The spread of the spectrum of a graph［J］．Linear Algebra Appl，2001，332-334:23-35．

［2］FAN Y Z，XU J，WANG Y，et al．The Laplacian spread of a tree［J］．Discrete Math Theor，2008，10:79-86．

［3］LIU M H，LIU B L．The signless Laplacian spread［J］．Linear Algebra Appl，2010，432:505-514．

［4］OLIVEIRA C S，LIMA L S，ABREU N M M，et al．Bounds on the Q-spread of a graph［J］．Linear Algebra Appl，2010，432:2342-2351．

［5］CVETKOVI'C D，ROWLINSON P，SIMI'C SK．Eigenvalue bounds for the signless Laplacian［J］．Publ Inst Math(Beograd)，2007，81(95):11-27．

［6］MERRISR．Laplacianmatrices of graphs:A survey［J］．Linear Algebra Appl，1994，197-198:143-176．

［7］PAN Y L．Sharp upper bounds for the Laplacian graph eigenvalues［J］．Linear Algebra Appl，2002，355:287-295．

［8］DAS K C．The largest two Laplacian eigenvalues of a graph［J］．Linear Multilinear A，2004，52:441-460．

［9］YOU Z F，LIU B L．The minimun Laplacian spread of unicyclic graphs［J］．Linear Algebra Appl，2010，432:499-504．

［10］CVETKOVI'C D，ROWLINSON P，SIMI'C SK．Signless Laplacians of finite graphs［J］．Linear Algebra Appl，2007，423:155-171．