关于恢复系数的再讨论＊

王 悦

（铜陵学院电气工程系 安徽 铜陵 244000）

关于撞击的首次科学上的研究，可追溯到1668年Kozlov［1］提出的碰撞理论，而碰撞恢复系数e是表征碰撞前后运动状态变化的重要参数.牛顿于1687年提出了通常的撞击行为往往既不是完全弹性碰撞，也不是完全非弹性碰撞.初始动能的损失可通过恢复系数e的引入来实现

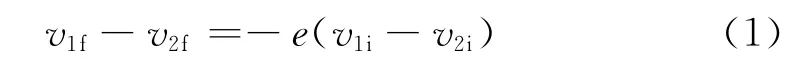
其中下标1和2分别表示撞击物和被撞击物，而i和f分别表示初始（initial）状态和最终（final）状态.e是个无量纲的系数，其值介于零和1之间，e为零对应于完全弹性状态，e为1对应于完全非弹性状态.这是经典力学中采用速度描述恢复系数的方法.

1 绝对恢复系数e的质疑

文献［2～5］对物体碰撞以及恢复系数进行了有益的探讨，其中文献［2］定义了一个物理量 ——绝对恢复系数，文献［5］针对它提出了质疑，文献［2］定义绝对恢复系数如下：一个物体的绝对恢复数等于它与一个完全弹性体发生互碰时，分离速度对接近速度的比值.经过较为严格的数学推演，得到了两个物体的共同恢复系数e与各自的绝对恢复系数e1和e2的关系为

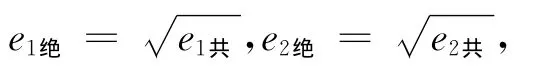
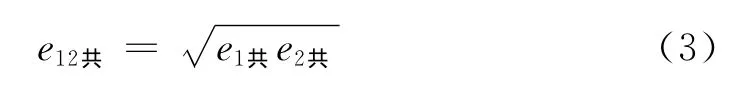
同时，还指出：公式（2）、（3）的形式极其简洁、美观，但实践是检验真理的标准.以铅、铁为例，由文献［6］查得，铅 －铅恢复系数e1共＝0.2，铁 －铁恢复系数e2共＝0.66，代入式（2）计算得到铅 －铁恢复系数为0.363，文献［6］给出值为0.14，它是实际铅 －铁恢复系数的2.6倍.理论与实际相差如此之大，使人们不得不重新考察理论的正确性.并且指出，如果有问题，只能出在物理上，其中绝对恢复系数是否存在唯一问题，是一个重要因素.

这里，我们先不讨论绝对恢复系数是否存在，对于上述，文献［5］根据文献［2］经过严格数学推导之后得到的公式（2）、（3），仔细观察就能发现其中的矛盾.现在我们假定，两个物体的共同恢复系数e与各自的绝对恢复系数e1和e2的关系式（2）正确，由对应关系推广到绝对恢复系数应该直接写成

而 不是式（3）！那么再把铅 －铅恢复系数为e1共＝0.2，铁 －铁恢复系数e2共＝0.66，代入式（3）计算得到铅 －铁恢复系数为0.132，此值与实验值0.14的相对误差仅有5.7%.

这个结果说明文献［2］的结论对实验还是有一定的指导意义.当然，文献［5］中提出的两不同材料的物体的恢复系数除了与它们自身的共同恢复系数（即同种材料的两物体碰撞恢复系数）有关外，至少还应该与它们各自的弹性模量有关.此观点也有一定的道理.而恢复系数究竟该如何定义？恢复系数本身和哪些因素有关呢？以下我们将做进一步的探讨.

2 恢复系数几种定义的讨论

我们对恢复系数的几种定义作进一步讨论.最初碰撞的恢复系数是由Newton引入的，正如我们前面提到的式（1）.他把碰撞前后法向分离速度与接近速度的比值定义为恢复系数e，由于这种定义在推广到一般性刚体碰撞时的局限性，于是出现了Poisson及Stronge对恢复系数的重新定义.Poisson将碰撞的过程分为压缩变形阶段及恢复变形阶段，恢复系数e被定义为恢复阶段的法向冲量与压缩阶段的法向冲量之比，而Stronge则定义为恢复阶段所释放的弹性应变能与压缩阶段所吸收的弹性应变能之比.三种定义的比较我们用下面的表1表示出来.

表1三种恢复系数定义的比较

已经证明，这些不同形式的恢复系数之间是有分歧的，仅在一定条件之下才能取得一致，从碰撞作用的特点来看，冲量比形式的定义较为可行，但更为直观的是速度比形式，因为碰撞是以速度突变的形式表现出来的，而能够直接测定的也只是速度；能量比形式在涉及能量转化的问题中有用.但是，速度、能量都和参考系的选择有关，不如碰撞冲量那样不随参考系而变.因此，速度比和能量比形式的恢复系数定义，不如冲量比形式简明.这就是大家倾向于采用后者的原因之一，至少在研究宏观物体的碰撞时是这样的，当固体以光滑面相接触而沿公法线方向发生正碰撞时，可以把恢复系数定义为碰撞第一阶段和第一阶段中两物体的碰撞点间相对速度变化量大小之比，或这两阶段中碰撞冲量的大小之比，或这两阶段中系统动能变化量大小之比取其平方根，这三者是完全一致的，甚至在物体进行着最一般运动的光滑的斜碰撞中，也可以证明这三个定义的等效性仍然成立.

仔细研究这三种定义，我们会发现一个共同特点是都将恢复系数看作为只与材料有关的常数.但是，大量的实验表明：恢复系数不是仅仅依赖于材料的一种固有属性，它还与摩擦、撞击物和被撞击物的材料、接触面的几何性质以及碰撞的位形、初始速度等因素有关［7］.在理论研究时，这三种定义是等同的；在工程中，一定要考虑到实际过程中的各种因素，这时三种定义都要做一定的修正.

3 结语

由上讨论可以知道，考虑到摩擦、撞击物和被撞击物的材料、接触面的几何性质以及碰撞的位形、初始速度等因素时，恢复系数不是仅仅依赖于材料的一种固有属性.而我们得到的式（3）中的“绝对恢复系数”是做了很大近似处理之后的结论，它可以作为处理一般的物体与物体之间发生碰撞时恢复系数的估算公式，更为精确的结果还是要依靠实验测量.希望我们的讨论，对今后恢复系数的认识和研究有一定的指导作用.

1 Kozlov，Valerii V.and Treshchёv，Dmitrii V.Billiards：A Genetic Introduction to the Dynamics of Systems with Impacts.American Mathematical Society，1991

2 康垂令.关于恢复系数e的讨论.大学物理，1997，16（12）：18～20

3 王长春.从能量的角度讨论两体碰撞问题.大学物理，2005，24（9）：18～19

4 吴红燕，于凤军.从弹性势能储能系数出发讨论两光滑小球的斜碰问题.大学物理，2007，26（2）：11～12

5 于凤军，贾栓稳.对绝对恢复系数的质疑.大学物理，2007，26（12）：16～17

6 南京工学院，西安交通大学.理论力学（下）.北京：人民教育出版社，1979.184

7 Goldsmith W.Impact.Edward Arnold Publishers Ltd.London，1960.262