三杆堆放的静力学问题

杨立楠 张元元

（中山纪念中学 广东 中山 528454）

静力学问题虽然在高考中逐渐淡化，但却是物理竞赛中的热点和难点问题，尤其是从2009年第26届全国高中物理竞赛后进行了一系列的改革，使得经典的静力学问题在竞赛中焕发了新的青春.本文从典型的三杆堆放问题出发，对解决静力学问题的思路做一个全面的分析.

问题1：为了简化情况，现有3根质量均为m，长为l的匀质细杆对称地搁置在粗糙的水平地面上，三杆的顶端O重合.此时底端A，B，C的间距也恰好为l，如图1所示.三杆能够静止时满足什么条件呢？

图1

处理问题的切入点就是接触处的静摩擦力不能超过最大静摩擦力.明确这一点，在处理过程中要想方设法解决接触处的弹力N和静摩擦力f的大小，静止的条件为f≤μN.如何解决呢？

（1）利用对称性

三杆底部受到的力的情况一致，即弹力的大小相等以及静摩擦力大小相等，有

（2）系统法分析

这在解决多体问题时要首先考虑的，受力分析后，必然满足合外力为零以及合力矩为零，判定静摩擦力方向.此时难点在于是否选择力矩平衡方程以及如何选择转轴.本题中系统的受力情况如图2所示，水平方向3个大小相等的摩擦力合外力为零，此时必然指向O的投影点O′，即△ABC的中心，这样才能保证三者方向间的夹角为120°.根据竖直方向合外力为零条件，有

图2

可知弹力N＝mg，此时是否要利用系统的力矩平衡方程呢？事实上我们已经判定了摩擦力的大小和方向，用隔离法更容易解决问题，这是需要观察与思考的.

（3）隔离法分析

这种分析方法也很常见，更是多体问题中定然用到的.本题中对OA杆进行分析，其受力情况如图3所示，根据弹力NA＝mg可断定OB和OC杆对OA杆的合力FA只能沿着水平方向与静摩擦力fA方向相反，此时有FA＝fA.处理过程可选择过A或者O的垂直纸面的转轴，但选择前者，力矩平衡方程更简单，则

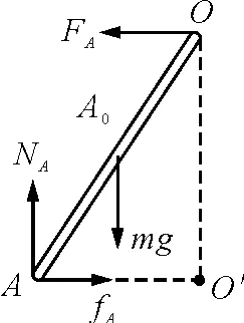
图3

（4）几何知识的应用

（5）静止条件f≤μN

通过式（3）可得到静摩擦力fA＝mg，可见系统平衡时杆与地面的摩擦系数μ满足

问题2：三杆堆放的情况同问题1一致，只是此时在OA的中点处固定一个质量也为m的小物体（可视为质点），此时三杆能够静止又满足什么条件呢？问题的条件尽管出现了变化，但处理问题的切入点却不变，只是此时要注意3个弹力（NA，NB，NC）、3个摩擦力（fA，fB，fC）和力FA的变化.

（1）利用对称性

只能判定NB＝NC，fB＝fC以及 NA不等于 NB和NC，此时fA的方向必定指向O′（这是因为无论大小相等的fB和fC无论是否指向O′，其合力一定指向O′A连线方向），但无法判定fB，fC的方向.通过对O C杆分析，如果fC不指向O′，如图4所示，4个力不在同平面，只要在O O′C平面内，选择通过杆的中心C0的竖直轴，重力mg和弹力NC的力矩为零，此时FC，fC的合力矩必然不为零，可见fB和fC必须指向O′，可见此时3个摩擦力必定大小相等.

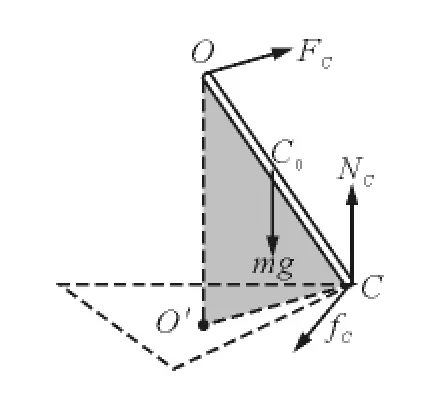
图4

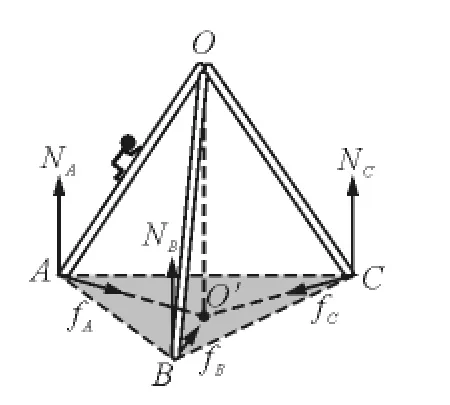
图5

（2）系统法分析

受力情况如图5所示，根据合外力为零条件有

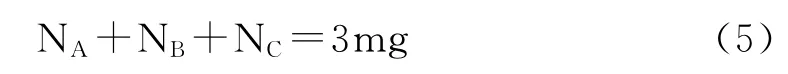
由于缺乏NA与NB（或NC）之间的定量关系，此时需要用到系统的力矩平衡方程，这与问题1中不同.为了尽可能简化力矩平衡方程，选择通过B，C的水平轴，5个力的力矩平衡（4个重力和NA），有

（3）隔离法分析

对OA杆进行分析，其受力情况如图6所示，但此时通过竖直方向两个重力与NA合力不为零可断定FA在竖直方向有分力FAy，即FA的方向不可能指向水平.但若选择通过O点垂直纸面的转轴，这无需考虑FA的方向和大小，有

最终解得

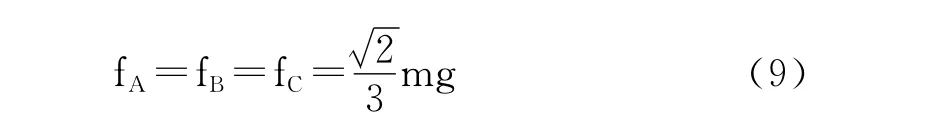
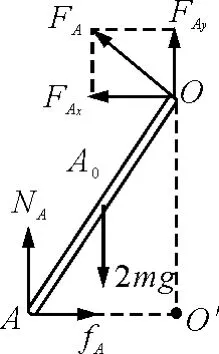
图6

结语：处理静力学问题，通常要利用系统法和隔离法进行受力分析，利用合外力为零和力矩平衡条件列相应的方程，从而解决问题.但如何选择合适的方法和方程，需要细心的体会以及通过比较与总结，慢慢形成处理静力学问题的体系，希望能够对读者有所启发.