一种改进的LDPC码硬判决译码算法
詹 尹,李宏伟
(空军工程大学信息与导航学院,陕西 西安 710077)
责任编辑:薛 京
低密度奇偶校验(Low Density Parity Check,LDPC)码是一种可以用稀疏校验矩阵或者因子图[1]来定义的线性分组码,该码最初由罗伯特·克拉克(Robert Gallager)[2]在其博士论文中提出,故亦称Gallager码。但是由于当时硬件条件有限,计算机的存储能力以及处理数据能力较低,LDPC码在此后相当长的时间里都未能引起编码理论界的重视,历经数十年的沉寂之后,随着计算机的高速发展,以及相关理论的出现(如置信传播算法),Mackay和Neal等人进一步完善了LDPC码的相关理论,为信道编码译码领域带来了继Turbo码后的又一个突破。在理论上,学者们发现LDPC码与之前的Turbo[3]码一样,都是能够逼近香农限的纠错码,其性能在某些条件下甚至还要好于Turbo码,这足以说明它的价值。在实际工程领域,LDPC码已经被成功地应用于多种系统,例如,中国地面数字电视广播标准(DTMB)[4],中国移动多媒体广播标准(CMMB)[5]等均已将LDPC码作为其的信道编码标准。毫无疑问,在不久的将来,LDPC码必然会广泛地应用于各种通信系统中。
根据译码判决准则的不同,LDPC的译码算法可以分为以后验概率为判决标准的软判决译码算法和以判决门限作为判决标准的硬判决译码算法。软判决译码算法方面,Gallager首先提出了置信传播算法(BP),Kschischang等人在此基础上对该算法进行了推广,提出了和积算法(SPA)[6],此后学者们又提出了一些和积算法的改进算法,目的主要在于降低算法的复杂度,例如最佳APP译码算法、对数域和积算法(LLR-BP)[7]、最小和算法(MS)[7]等。
在硬判决算法方面,最具有代表性的是由Gallager提出的基于判决门限的比特翻转算法(BF)[2],该算法操作简单、复杂度较低、易于硬件实现,但是其性能比较差,因此,为了提高算法的性能,Kou Y等人对BF算法进行了改进,提出了加权比特翻转(WBF)[8-9]算法,该算法在每一轮的迭代中,都对每个变量节点进行可靠性计算,并翻转可靠性最小的变量节点,大大提高了性能,但是由于每轮迭代只能翻转一个变量节点,且需要引入可靠性的计算,导致算法的复杂度增加。
本文在已有硬判决算法的基础之上,对WBF算法进行了改进,改进的算法在前两轮迭代中可以同时翻转多个变量节点,使得译码的运行时间大大减少。仿真结果表明,改进后的译码算法在高信噪比条件下的译码性能要好于传统的算法,并且能够降低WBF算法的复杂度,减少译码的迭代次数,从而兼顾译码性能与译码效率。
1 传统硬判决算法
1.1 BF 算法
由Gallager提出的基于判决门限的比特翻转算法(BF)操作简单,复杂度较低,且易于硬件实现,在LDPC码译码领域曾经得到广泛的应用,下面就从BF算法开始,介绍其译码原理,以及基于其的改进算法WBF。
考虑一个二进制的规则LDPC码,码长为N,信息位的长度为K,其校验矩阵为一个M×N的稀疏矩阵,即H={hmn}(0≤m≤M -1,0≤n≤N-1),“稀疏”体现在校验矩阵中只有极少量的“1”,其余位置由“0”组成。对于二进制的规则LDPC码,其校验矩阵每行“1”的个数都相同,设为q,表示每个校验方程中所包含的码元数目相同,这些码元都受到该校验方程的约束;校验矩阵每列所包含的“1”的个数也相同,设为p,表示每个码元都参与了p个校验方程,即被p个检验方程约束。Gallager在提出LDPC码后,就证明了当p≥3时,这类码的汉明距离特性非常好。
在信息传输的过程中,要发送的信息码字通过信道编码后得到带有校验码的二进制码字序列v=[v0,v2,…,vN-1],该序列通过 BPSK 调制,按照映射 rn=1 -2vn,得到一个对应序列 r= [r0,r1,…,rN-1];然后该序列进入信道,信道为一个AWGN信道,其均值为0、方差为N0/2;通过信道后,得到输出序列 y=[y0,y1,…,yN-1],根据输出序列y进行判决,就可以得到每个比特的二进制硬判决值 z= [z0,z1,…,zN-1],即

在信息通过信道进行传输的过程中,由于噪声等因素的干扰,会使得信号遭到破坏从而导致误码,这时,那些错误码元将不再满足各自所参与的校验方程。比特翻转算法(BF)正是根据这一性质,在每一轮的迭代过程中,先根据上一轮每个比特的硬判决值计算每个校验方程的值zn,如果每一个校验方程都为0,也就是可以认为判决序列满足所有校验方程,则停止迭代,译码成功;否则,需要计算每位比特所不满足的校验方程的个数,即在其参与的所有校验方程中,校验和为1的方程的个数,如果在某些比特所参与的所有检验方程中,其不满足校验方程的个数大于预先设定好的判决门限T,那么就将这些比特进行翻转,由此就能得到一个新的判决序列,然后进入下一轮的迭代,直到所有校验方程都满足,或者达到最大的迭代次数,译码失败。在上述译码过程中,门限T的选取非常重要,其对于译码性能的影响非常大。
BF算法流程如下:
1)根据硬判决序z=[z0,z1,…,zN-1]列以及校验矩阵H,利用式(2)计算错误伴随图样s= [s1,s2,…,sm],如果s为0,则迭代停止,输出判决序列;否则,进入步骤2)。

2)在每个码元所参与的校验方程中,计算其不满足校验方程的个数,记作

3)如果fn>T,那么翻转zn,得到新的比特值。
4)重复前3步直至译码成功,即s=0,或者达到最大迭代次数,即译码失败。
从算法步骤可以看出,BF算法只需要在二进制域进行简单的逻辑运算,实现非常简单,但其性能和软判决译码算法相比较差,因此,应用于对LDPC码进行粗略的译码,或者是信道条件很好的情况下。
1.2 WBF 算法
传统的BF算法只需进行简单的逻辑运算,易于实现,且操作简单,但是其性能较差,这是由于其比特翻转的依据是该比特所对应的不满足校验方程的数目,这样的判决依据并不精确。经过研究分析,Kou Y等人发现,对于一组接收比特 y= [y0,y1,…,yN-1]中的任意一位比特 yn,其可靠性都可以用自身的绝对值来度量,也就是说,该接收比特的绝对值越大,对其进行的判决值就越可靠。基于这个原理,在传统的BF算法中引入了每个校验方程的可信度以及每一个比特的权重等软信息,提出了加权比特翻转(WBF)算法。
在每一轮的迭代过程中,WBF算法利用参与每个校验方程的输出比特的最小幅值对每个变量节点进行加权,计算翻转函数,并认为翻转函数值最大的比特出现了错误,应进行翻转。定义N(m)={n|hmn=1}表示参与第m个校验方程的比特的集合,M(n)={n|hmn=1}表示第n个比特参与的校验方程的集合,那么第m个校验方程的可信度表示为

也就是说,如果一个校验方程所对应的比特的最小绝对值大于另一个校验方程所对应的比特的最小绝对值,那么该校验方程的可信度就更高。
WBF算法首先依据上一轮的判决序列计算每个校验方程的值,验证是否满足校验方程,如果所有的校验方程都满足,那么停止迭代,译码成功;否则,根据式(4)计算每个校验方程的可信度,并且对每个码元进行加权,计算每个码元的翻转函数,即

对翻转函数最大的码元比特进行翻转,得到新的判决序列,如果新判决序列满足所有校验方程,或者译码过程达到了最大迭代次数,那么译码结束;否则,进入下一轮迭代。
WBF 算法流程如下[10]:
1)根据硬判决序列z=[z0,z1,…,zN-1]以及校验矩阵H,利用式(2)计算错误伴随图样 s= [s0,s1,…,sm],如果s=0,则迭代停止,输出判决序列;否则,进入步骤2)。
2)对于m=0,1,…,M -1,利用式(4)计算每一个校验方程的可信度。
3)对于n=0,1,…,N -1,利用每个校验方程的可信度,对相应的码元进行加权,利用式(5)计算每个码元的翻转函数,并将翻转函数值最大的码元进行翻转,得到新的判决序列。
4)重复前3步,直到所有校验方程都被满足,输出判决序列,译码成功;或者达到最大迭代次数,译码失败。
与传统的BF算法相比,WBF算法引入了实数加权处理,可以更加有效地对错误比特进行定位,获得译码性能的提高,但是加大了算法复杂度,增加了计算量。此外,该算法还有一个很大的缺陷,由于每一轮迭代只是将翻转函数最大值所对应的比特翻转,因此一轮迭代仅仅能翻转1比特位,这样必将增大迭代的次数,影响整体译码的速度。
2 改进的加权比特翻转算法
当今的通信系统对于实时性要求越来越高,需要在确保整体译码性能较好的基础上,尽可能实现快速译码,通过上述分析可以看出,WBF算法并不能满足这一要求。
传统BF算法可以同时翻转多个比特位,这是因为其引用了判决门限T,因此可以设想,如果对WBF算法也引入判决门限T,将翻转函En数大于T的比特都进行翻转,就可以在每一次迭代中同时翻转多位比特,提高译码的效率。此外,为简化算法的复杂度,更好地兼顾译码性能和译码效率,仅仅将判决门限应用在改进算法的前两次迭代过程中。
在WBF算法中,比特翻转函数的信息仅仅是来自校验关系,而在改进的RWBF算法中,翻转函数还考虑了比特自身的信息,即把每个输出比特的绝对值也引入到其所对应的翻转函数中,这样就兼顾了比特自身的信息以及来自校验关系的信息,使得翻转函数的定义更加准确,改进后的翻转函数定义为
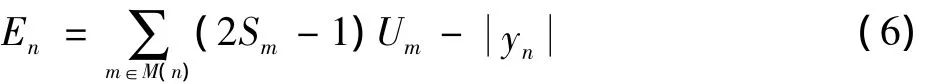
需要强调的是,判决门限值T并不是固定的,它将随着LDPC码参数的不同而改变,为了获得最佳的译码性能,可以由仿真来确定。
RWBF算法流程如下:
1)根据硬判决序列z=[z0,z1,…,zN-1]以及校验矩阵H,利用式(2)计算错误伴随图样 s= [s0,s1,…,sm],如果s=0,则迭代停止,输出判决序列;否则,进入步骤2)。
2)对于m=0,1,…,M -1,利用式(4)计算每一个校验方程的可信度。
3)对于n=0,1,…,N -1,利用每个校验方程的可信度,对相应的码元进行加权,利用式(6)计算每个码元的翻转函数。
4)如果迭代次数是1或者2,那么将所有的翻转函数值大于判决门限T的比特都进行翻转;如果迭代次数大于2,那么将翻转函数值最大的比特进行翻转。
5)重复前4步,直到所有校验方程都被满足,输出判决序列,译码成功;或者达到最大迭代次数,译码失败。
从上述的译码流程可以看出,RWBF算法在迭代次数大于2之后,其复杂度以及计算量与WBF算法完全相同,但是在前2次迭代中,该算法可以翻转多个比特,而WBF算法每一次迭代都只能翻转1位比特,因此RWBF算法具有比WBF算法更快的译码速度。
3 仿真分析
仿真采用IEEE802.16e标准,LDPC码码长N=2 304,码率R=5/6,调制方式为BPSK,用于观察传统的BF、WBF硬判决算法和本文提出的改进型译码算法RWBF的误码率性能。仿真所采用的是高斯白噪声信道(AWGN),仿真平台为MATLAB,实验采用蒙特卡洛法,每个信噪比下实验1 000次,算法仿真结果如图1、图2所示。
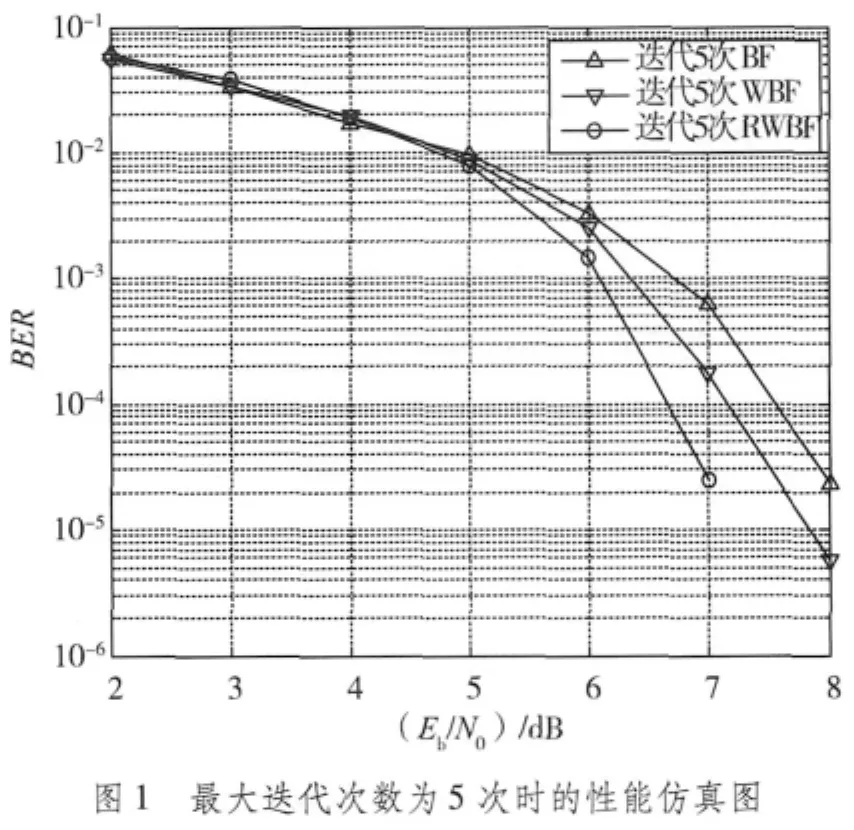
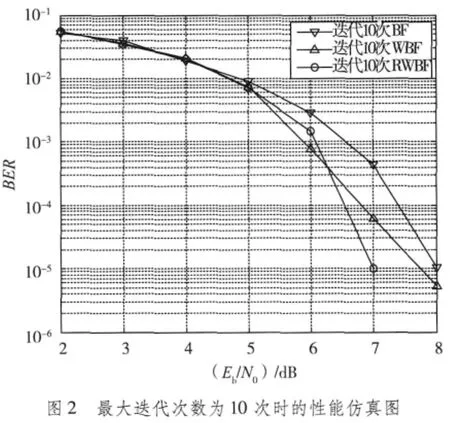
图1、图2中分别仿真了LDPC译码过程中最大迭代次数分别为5次和10次时,BF,WBF和RWBF算法的性能。从图中可以看出,随着最大迭代次数从5次增大到10次,3种算法的性能都得到了一定的提高。当信噪比小于5 dB时,3种算法的性能相差不大,而在性噪比大于5 dB的高信噪比下,最大迭代次数的选取将会影响到算法的性能:最大迭代次数为5次,RWBF译码算法(β=0.5)性能明显好于BF以及WBF算法;最大迭代次数为10次,当信噪比大于6.5 dB时,RWBF译码算法在性能上比BF以及WBF算法好,在BER=10-5,RWBF算法比WBF算法性能提高近1 dB,但是信噪比在5~6.5 dB之间时,RWBF算法性能与WBF算法相比略有下降。此外,RWBF算法的最大译码迭代次数从10次变为5次时,性能并没有明显降低,而BF和WBF算法迭代次数变少时,译码性能恶化较为明显。因此,对于RWBF算法而言,可以在保证译码性能的前提下,适当减少迭代次数,兼顾算法的性能和复杂度。
4 结论
LDPC码是能够逼近香农限[11]的纠错码,它良好的应用前景已经引起学术界以及IT业的高度重视。本文在传统的硬判决BF算法、WBF算法的基础之上进行了改进,改进的算法在译码的迭代过程中引入了判决门限,可以同时翻转多个比特,因此,能够降低译码的迭代次数,使得译码的运行时间大大减少。此外,考虑到如果让每一个比特所对应的翻转函数都与门限T比较,势必将增加多余的计算,增大算法的复杂度。因此,为了更好地兼顾译码性能和译码效率,仅仅将判决门限应用在改进算法的前两次迭代过程中。仿真结果表明,与传统算法相比,改进算法的译码性能不但不会下降,在高信噪比条件下还能得到一定提高。因此,该算法能够在保持良好译码性能的同时降低算法的复杂度,这使得LDPC码能够更好地应用在4G移动通信系统[12]中。
[1]LOELIGER H A.An introduction to factor graphs[J].IEEE Signal Processing Magazine,2004,21(1):28-41.
[2]GALLAGER R C.Low-density parity-check codes[M].Cambridge,MA:MIT Press,1963.
[3]朱联祥,杨士中,汪纪锋.基于因子图的Turbo码译码[J].重庆大学学报:自然科学版,2002(7):40-44.
[4]杨知行,王昭城.下一代地面数字电视广播系统关键技术[J].电视技术,2011,35(8):22-27.
[5]张鹏,杨刚,杨霏,等.基于改进LU分解的CMMB标准中LDPC编码器设计[J].电视技术,2010,34(4):33-35.
[6]CAMPELLO J,MODHA D S.Extended bit-filling and LDPC code design[C]//Proc.IEEE Global Telecommunications Conference.[S.l.]:IEEE Press,2001:985-989.
[7]FOSSORIER M P C,MIHALJEVIC M,IMAI H.Reduced complexity iterative decoding of low-density parity check codes based on belief propagation[J].IEEE Trans.Communications,1999,47(5):673-680.
[8]KOU Y,LIN S,FOSSORIER M P C.Low density parity check codes based on finite geometries:a rediscovery and new results[J].IEEE Trans.Information Theory,2001,47(7):2711-2736.
[9]ZEIDAN H R,ELSABROUTY M M.Modified iterative two-stage hybrid decoding algorithm for low-density parity-check(LDPC)codes[C]//Proc.IEEE 69th Vehicular Technology Conference.[S.l.]:IEEE Press,2009:1-5.
[10]ZHANG J,FOSSORIER M P C.A modified weight bit-flipping decoding of low-density parity-check codes[J].IEEE Communications Letters,2004,8(3):165-167.
[11]彭代渊,蒋华,郭春生,等.信息论与编码理论[M].武汉:武汉大学出版社,2008.
[12]杨宇良.穿越20年:通信技术进化论[J].软件工程师,2011(11):14-20.

