最大边缘准则图形嵌入在人脸识别中的应用

宋宇翔，胡 伟

(1.广东培正学院计算机科学与工程系，广东 广州 510830;2.湖南第一师范学院科研处，湖南 长沙 410002)

责任编辑:时 雯

人脸识别因其在人机交互、图像处理和计算机视觉方面的应用，已经成为近年来的研究热点。局部邻接降维方法的目的是为了一个嵌套在高维空间中的有效子空间，该子空间能有效地表示高维空间中的数据并且保持高维数据的非线性结构。线性判别分析保护了数据间的判别信息以及通过最大化类间矩阵与类内矩阵的比例来找到最优投影轴。

PCA［1］、LDA［2］以及类似算法不能很好地表示数据潜在的非线性数据结构。许多最新的流形学习算法提出了保持局部邻接关系的思想。比如局部邻接嵌入LLE(Locally Linear Embedding)［3］、拉普拉斯映射。文献［4］提出了局部保持投影算法，该方法是一种起源于拉普拉斯映射的线性子空间方法。LPP［4］能够找出一个保持局部邻接信息的线性子空间，它是一种无监督学习方法，许多变种LPP［4］方法考虑了判别信息。

上述学习算法可以被统称为线性图嵌入框架的一种推广，不同的是利用不用的矩阵和权重。然而，上述方法也存在一些限制，比如LPP［4］、LLE忽略了类别信息，从而降低了识别率。其他限制如LDE、边界Fisher分析［5］和DLPP［6］涉及到判别矩阵的伪逆矩阵问题，同样会降低识别率［7－8］。本文在提出一种新方法的，同时考虑了局部图嵌入和最大化边界标准［9－10］，该方法不必将图像矩阵转换成一个图像向量，从而节约了计算时间避免逆矩阵。

1 算法设计与分析

假定给定的训练样本数目比较小，线性判别方法如LDA［2］，LPP［4］的类内离散度矩阵会出现奇异情况，因为需要奇异矩阵的逆，则给利用这些方法造成一定的困难。最大边界标准MMC［9］是一种寻找类间与类内离散度矩阵最小化的差值，本文提出一种新的方法，即最大边界的局部图嵌入方法(EM/MMC)。该方法寻找最小化局部邻接类间离散度矩阵和局部邻接类内离散度矩阵的差，而不是二者之间的比率，因而奇异值的情况可以被避免。为了获得这些判别向量，同时最小化局部保持类间离散度矩阵和最大化局部保持类内离散度矩阵。

1.1 局部保持类内离散度矩阵

该方法通过一个节点的邻接节点及线性权重重建该节点从而最小化数据样本的紧凑性。表示过程和LLE［3］类似，LLE根据最近邻思想把每个与该节点最相邻的几个节点作为表示该节点的特征节点。

第一步，LLE［3］算法根据最近邻思想使用欧式距离找出与每个数据点最近的特征节点。

第二步，计算重建权重矩阵W，根据最近邻点来重建每个点。最小化重构误差来获得系数矩阵W，即

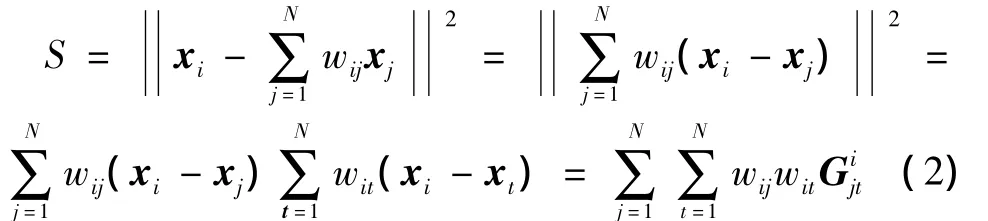
对所有训练样本执行完第一步和第二步之后，可以计算出权重矩阵 W= ［wij］N×N。

第三步，通过权重矩阵W重建每个数据点yi，为了保持在重建过程中数据的内在几何特征结构，最小化重构误差函数

式中:yi是yj的邻接点。

重构误差函数由式(4)可进一步化简为

其中，M=(I－W)T(I－W)。

1.2 局部保持类间离散度矩阵

最大化局部保持类间离散度矩阵，可以通过式(6)得出

其中，yi和yj是类别输出。

目标函数式(6)可进一步化简

1.3 基于最大边缘准则图形嵌入方法(EM/MMC)

局部保持类间离散度矩阵和局部保持类内离散度矩阵计算出来以后，通过式(5)、式(7)进而计算投影矩阵，即

约束优化问题式(8)就是寻找一个子空间，同时最大化局部保持类间离散度矩阵和最小化局部保持类内离散度矩阵。上述优化问题式(8)可以转换为

其中，u是一个平衡类内矩阵与类间矩阵的参数。通过引入拉格朗日乘子法解决如上约束优化问题，即

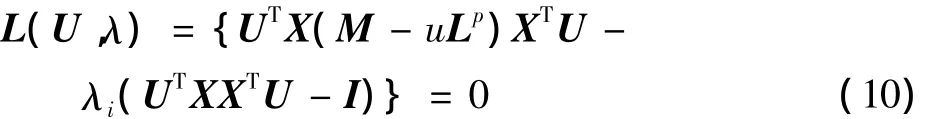
其中，λi是拉格朗日乘子。式(10)进而得到

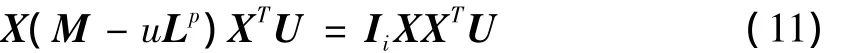
其中，λi和U是相应的特征值与特征向量。

2 实验

2.1 人脸库

实验采用两个流行的人脸库，Yale人脸库及ORL人脸库。

Yale人脸库包含了15个人的165张人脸，每人11张，包括了不同光照条件(灯光往左照射、往右照射、往中间照射)，不同的面部表情(正常的、开心的、沮丧的、睡着的、惊讶的以及眨眼的)，不同场景的(戴眼镜的和不戴眼镜的)，如图1所示为Yale人脸库中一个人的11幅具有不同特征的人脸图像。

ORL人脸库共有40个人的400张图片，每人10张，其中有些图像是拍摄于不同时期的，人的脸部表情和脸部细节有着不同程度的变化，如图2所示为ORL上某人的10张图片。

图1 Yale人脸库中某人的11幅人脸图像

图2 ORL人脸库中某人的10张人脸图像

2.2 实验结果及其分析

将本文方法与几个文献中的方法进行了比较，如PCA［1］，LDA［2］，LLE［3］，MMC［4］，LLE+LDA［5］，所有方法的投影矩阵都是由训练样本计算得来，所有的样本，包括训练样本、测试样本都投影到特征子空间，然后利用欧氏距离与最近邻原则完成人脸的识别，并且都在同一台PC机上完成。实验中，随机选取了每个人的2～6张图像作为训练样本，剩下的所有图像作为测试样本，实验结果如表1、表2所示。

表1 各个方法在ORL上的识别率

表2 各个方法在Yale上的识别率

由表1及表2可以看出，在训练样本取2～6张的各种情况下，它的优越性均显而易见。为了更好地体现出本文方法的优越性，将几个文献中的方法与本文方法在时间复杂度(包括训练阶段的、测试阶段)、空间复杂度做了比较，如表3所示。其中，m和n分别表示图像矩阵的行数和列数，L，M，N分别表示投影向量数、测试样本数、训练样本数。

表3 各个方法的时间复杂度比较

从表3可以看出，本文方法在训练阶段时的时间复杂度稍微有点高，但是较LLE+LDA方法还是有明显的优势的，测时间段的时间复杂度、空间复杂度都不必其他方法逊色，甚至比LLE+LDA［8］方法低得多。

综上所述，本文方法较 PCA［1］，LDA［2］，LLE［3］，LLE+LDA［8］，MMC［9］方法，虽然在复杂度方面没有大的改善，但是在识别率方面有了很大提高，这也正是本方法解决的最重要的问题。

3 结束语

在模式识别中，人们广泛使用特征提取技术来降维及其完成识别工作，本文提出了一种特征提取与识别的新方法，在ORL和Yale上的实验表明，本文方法的具有高识别率及高效率。下一步将会在其他的数据集上进行实验，改变其他的参数，如μ，Kc，Kp，以进一步研究本文方法的识别效果。同时，可以把EM/MMC方法扩展为监督、半监督的方法。

［1］刘晓杰，王世亮，张志伟.Gabor小波和LPP相结合的人脸识别方法研究［J］.电视技术，2011，35(23):121－124.

［2］LIAO P，LIU J，WANG M，et al.Ensemble local fractional LDA for face recognition［C］//Proc.CSAE 2012.［S.l.］:IEEE Press，2012:586－590.

［3］ROWEIS S T，SAUL L K.Nonlinear dimensionality reduction by locally linear embedding［J］.Science，2000，290(5500):2323－2326 .

［4］HE X，YAN S，HU Y.Learning a locality preserving subspace for visual recognition［C］//Proc.9th ICCV.Nice，France:IEEE Press，2003:385－392.

［5］HU H.Orthogonal neighborhood preserving discriminate analysis for face recognition［J］.Pattern Recognition，2008，41(5):2045－2054.

［6］YANG L，GONG W，GU X，et al.Null space discriminant locality preserving projections for face recognition［J］.Neurocomputing，2008，71(16):3644－3649.

［7］WANG Y，WU Y.Complete neighborhood preserving embedding for face recognition［J］.Pattern Recognition，2009(43):1008－1015.

［8］YAN S C，XU D，ZHANG B Y，et al.Graph embedding and extensions:A general framework for dimensionality reduction［J］.IEEE Trans.Pattern Anal.Mach.Intell.，2007，29(1):40－51.

［9］HUN D，FEN G，ZHOU S.Two dimensional locality preserving projections with its application to palm print recognition［J］.Pattern Recognition，2007，40(1):339－342.

［10］张爱华，尉宇.基于混沌粒子群的决策树SVM的调制模式识别［J］.电视技术，2012，36(23):126－129.