基于Theodorsen方法的螺旋桨空泡数值计算研究
赵 鹏 周玉龙 赵鹏飞 杨 超
(江苏科技大学 船舶与海洋工程 镇江212003)
0 引 言
避免或推迟螺旋桨空泡的产生对螺旋桨设计意义重大。如今,应对螺旋桨空泡问题的主流方法是采用空泡斗校核[1-2],该方法虽然简单易行,但对于桨叶剖面是否会出现空泡,只能进行粗略判断,无法细化到空泡产生的具体位置;而面元法[3-5]虽然能较好地预报桨叶上的空泡形状与位置,但计算量相对较大,运算周期长[6]。
目前已广泛应用升力线、升力面理论方法来设计螺旋桨,可初步得到一个桨叶剖面形状(见下页图1)及各项有关性能参数,然而无法得到桨叶剖面上的压力分布,因此不能直接对螺旋桨空泡性能进行预报。针对这一缺陷,本文使用Theodorsen法[7]及边界层修正[8],来计算桨叶剖面有关各点的压力,将所得桨叶剖面各点压力系数与该点空化数进行比较,从而对空泡进行初步预报,判断桨叶剖面上空泡出现的位置,为螺旋桨设计者调整各项参数以改善空泡性能提供依据。主要内容如下:

图1 初步提供的桨叶剖面

图2 进行坐标调整后的桨叶剖面
(1)整理出由Theodorsen法和边界层修正来预报空泡的整体思路;
(2)对有攻角的桨叶剖面进行坐标转换,使其满足Theodorsen方法的要求;
(3)对近似圆中坐标点所需进行的线性拟合的目标函数定义为三角函数;
(4)边界层修正时,为便于计算,将边界层厚度的修正转换到极坐标系中进行;
(5)以HSP桨作为算例,计算桨叶r/R=0.7处,剖面在旋转至 0°、90°、180°、270°时的非定常压力系数,对该剖面在各角度处是否出现空泡或空泡位置作出推断;计算了桨叶r/R=0.7处,剖面在0.25弦长、0.4弦长、0.6弦长、0.8弦长位置旋转一周的压力变化。
1 计算方法
1.1 Theodorsen法
Theodorsen法的基本思想是先把给定的桨叶剖面周线通过儒可夫斯基变换式转换为近似圆,再利用特定的级数形式的变换函数将近似圆变换为准确圆,求得桨叶剖面绕流速度分布与桨叶剖面坐标的关系。由伯努利方程可知,在已知速度分布的情况下,可求得桨叶剖面各点的压力分布。
在ζ平面上给定一个桨叶剖面,其周线为C,弦长l=4a。以弦线中点为原点建立坐标系,令前缘点A点坐标为(-2a,0),T 点坐标为(2a,0),见图 2。
通常由升力线、升力面初步计算得出的桨叶剖面形状均有一定的攻角α,并不适合Theodorsen法坐标系的建立。因此需对该桨叶剖面初始坐标(s,t)点进行坐标旋转,转换如下:

式中:

然后,通过下列儒可夫斯基变换式将桨叶剖面周线C变换为z′平面上的近似圆。

令z′平面上复数为:
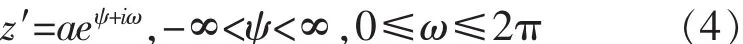
式中:Ψ和ω是z′平面上复坐标变量。将式(4)代入式(3),建立变换的对应关系:
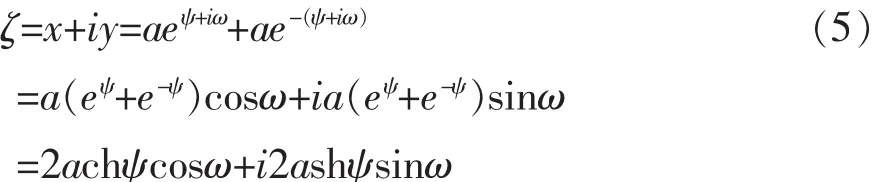
所以有
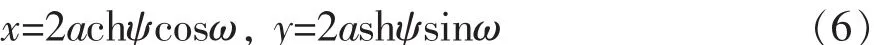
从式(6)可解得ω和ψ为
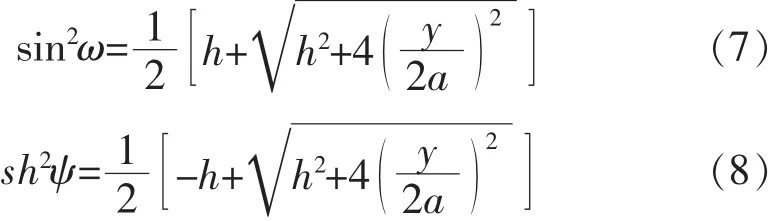
因此,根据桨叶剖面坐标(x,y),便可通过式(7)、式(8)确定近似圆上对应点处极坐标变量ω和ψ,并对离散点Ψ(ω)进行拟合、求导,最终得到。
通过对NACA66 a=0.8(Mod)的某桨叶剖面的计算,得到数据如图3所示。
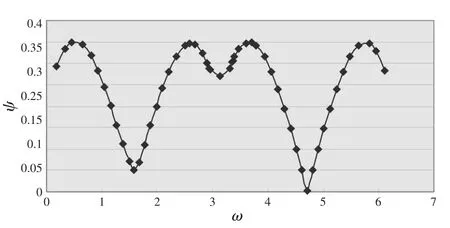
图3 桨叶剖面各点在z′平面内的坐标分布
通过图3对离散点分布的观察,可将叶背、叶面曲线拟合的目标函数分别定义为:
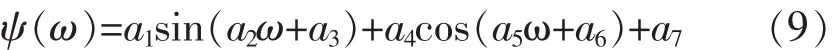
对叶背曲线的拟合如图4所示。
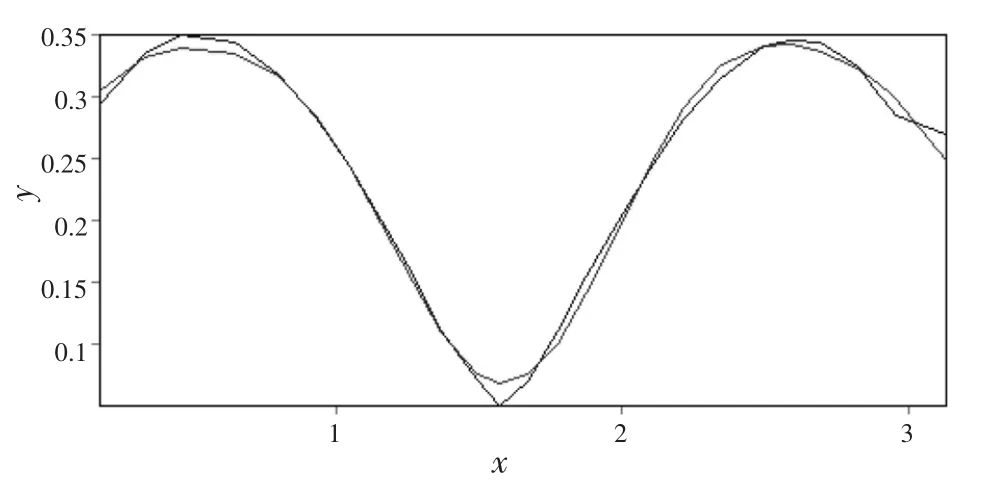
图4 离散点曲线与拟合的函数间的关系
本文采用 Levenberg-Marquardt法[9]对目标函数各变量进行计算,通常其相关系数均可达到0.995以上。
下一步,利用级数形式函数式(10)与式(11),将z′平面上近似圆变换到z平面上为一准确圆。
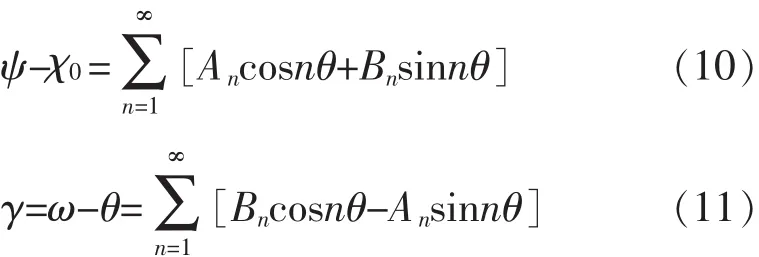
对式(10)利用求三角级数系数的方法,可得常数
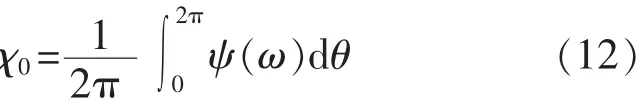
从而可得z平面上圆半径

根据共轭三角函数关系知γ与ψ是共轭的(因χ0是常数)。 如果已知 ψ(θ),则 γ(θ)就可确定。 由泊松公式可知:

式中:γ0= (ω-θ)0表示 θ-θ0(特定值)时的 γ 值。 然而,我们知道的是ψ(ω),尚不知道ψ与θ之间的关系。但因为近似圆C1与圆S相差并不太大,可假定θ与 ω 之差不大,而令 ψ=ψ(ω)=ψ(θ)作为第一级近似,因此,将它代入式(14),可得到 γ=ω-θ的第一级近似的 γ0(1)。
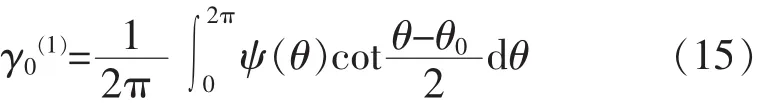
求出 γ0(1)后,于是得到 ω=θ+γ0(1)。 将 ω=θ+γ0(1)代入 ψ=ψ(ω)=ψ(θ+γ(1))后,可得 γ 的第二级近似:

以此类推。但是,实际上第一级近似已有满意的结果,然后求出 γ(2)=γ(2)(ω)的数值关系,以及的分布。
第四步,根据式(12)、(13)求得 χ0、r0。
第五步,根据Kutta条件,对应于z平面上圆柱绕流,应规定这一点(θ=-γ处)为后驻点,以保证桨叶剖面绕流在尾缘处的速度为有限值。

第六步,将上述求得的结果代入式(18)
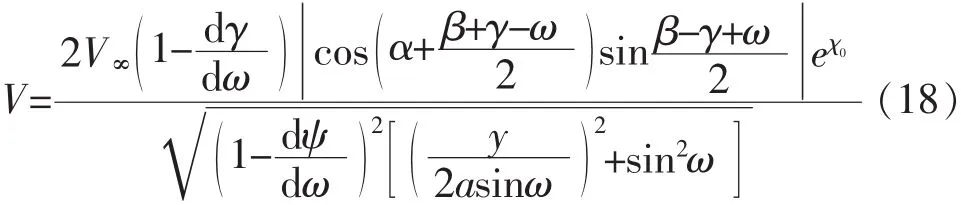
由式(18)便可求得桨叶剖面上速度与ω之间的关系。式中α为来流攻角,可在合理范围内任意给定。因式(7)、式(8)已确定 ψ、ω 与桨叶剖面上(x,y)的关系,所以沿桨叶剖面上速度分布也随之求出。
1.2 边界层修正
势流理论是基于理想流体对速度分布、压力分布进行求解,该解必须经过粘性修正才能与实验结果基本相符。本文采用边界层修正来近似替代粘性对桨叶剖面的影响。
假定使用Theodorsen法进行计算得到的速度势流解作为边界层外缘处的速度分布,引入边界层位移厚度 δ1(x)和边界层动量厚度 δ2(x):
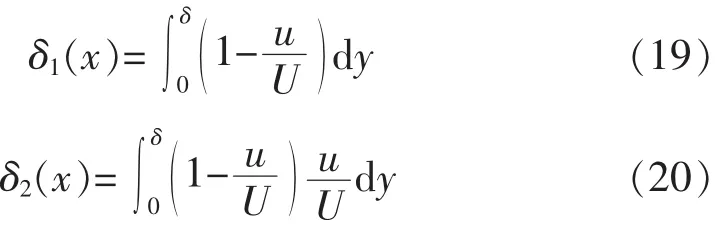
并定义动量厚度雷诺数

引入形状因子

为便于使用,将边界层动量积分方程写为:

式中:Cf为摩擦系数

单独由动量积分方程式(23)无法求解,因此必须补充方程。在计算层流边界层时,本文使用Thwaites法来求解动量积分厚度和位移厚度;对于紊流边界层的计算,则采用Head法所提出的补充方程进行求解,用修正后的米歇尔(Michel)经验公式进行转折点的判断:

式中:RexT
为Michel基于实验提出的转折点位置XT处的雷诺数。
下面分别对层流和湍流边界层进行计算。
1.2.1 使用Thwaites法对层流边界层进行计算

最终便可求得位移厚度 δ1= δ2·H12。
1.2.2 使用Head法对紊流边界层进行计算
Head法针对动量方程提出两个补充方程:
(1)卷吸积分关系式:
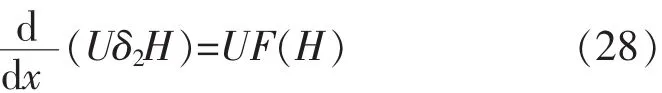
由实验数据确定其中变量

(2)摩擦系数关系式:
摩擦系数Cf与动量厚度雷诺数Re2有关,利用Ludwieg和Tillmann提出的关系式:
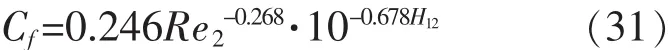
由式(23)、(29)、(30)、(31)可组成封闭方程,从而可求出 δ2、H12、δ1。
在求得ζ平面上的位移厚度δ1(x)后,将其转化为 Z′平面内的位移厚度 δ1z′(ω),然后对原桨叶剖面进行粘性修正,其叶背、叶面处的修正分别为:
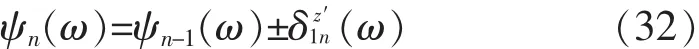
将物面外推δ1z′(ω),对包括排挤厚度的桨叶剖面再作势流解,重复Theodorsen法各个步骤,便是粘性修正后的初次近似结果。将该近似结果继续进行边界层修正,反复迭代,直至迭代结果满足精度要求。式(32)中n为迭代次数。得到满意的速度分布后,可由伯努利方程推导出桨叶剖面压力系数分布:

1.3 空泡校核
空化数计算公式:

由此,可比较桨叶剖面各点处的压力系数与空泡数大小,从而判断该点处是否会产生空泡。
2 结果分析
对HSP桨桨叶0.7半径处剖面进行压力分布计算。表1所示为HSP螺旋桨的主要参数;表2所示为该桨的试验工况。

表1 HSP螺旋桨的主要参数

表2 HSP桨的试验工况
表3所示为该桨的桨叶几何参数,图5是该桨的伴流分布。

表3 HSP桨叶型值

图5 HSP的伴流分布
图6为HSP桨0.7半径剖面的非定场压力系数(0°)。由图6可推断,桨叶转到此角度时,桨叶剖面自接近导边至x/C=0.45处压力系数均大于空泡数,因此可推知此段桨叶会产生空泡。
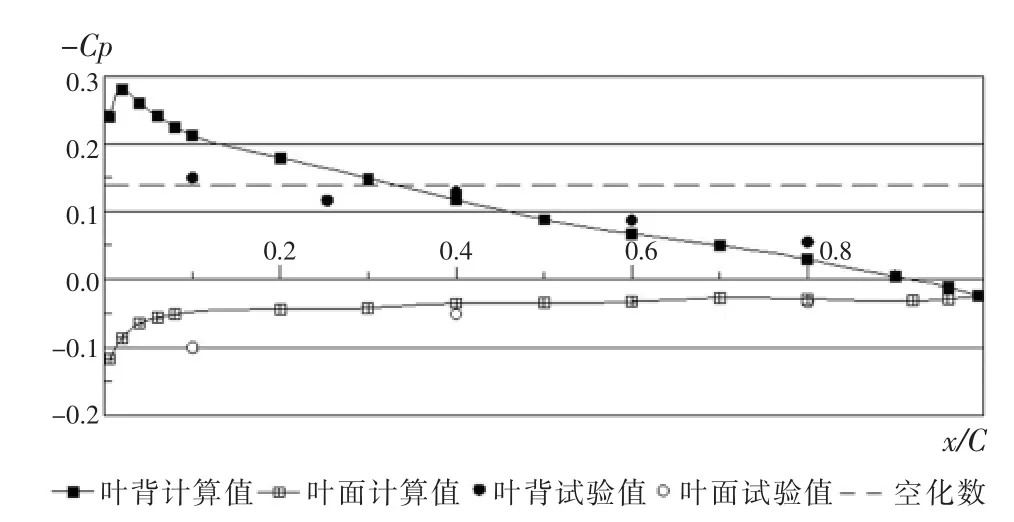
图6 HSP桨0.7半径剖面的非定场压力系数(0°)
图7为HSP桨0.7半径剖面的非定场压力系数(90°)。由图7可推断,桨叶转至此角度时,桨叶剖面各处压力系数均小于空泡数,因此可推知不会产生空泡。
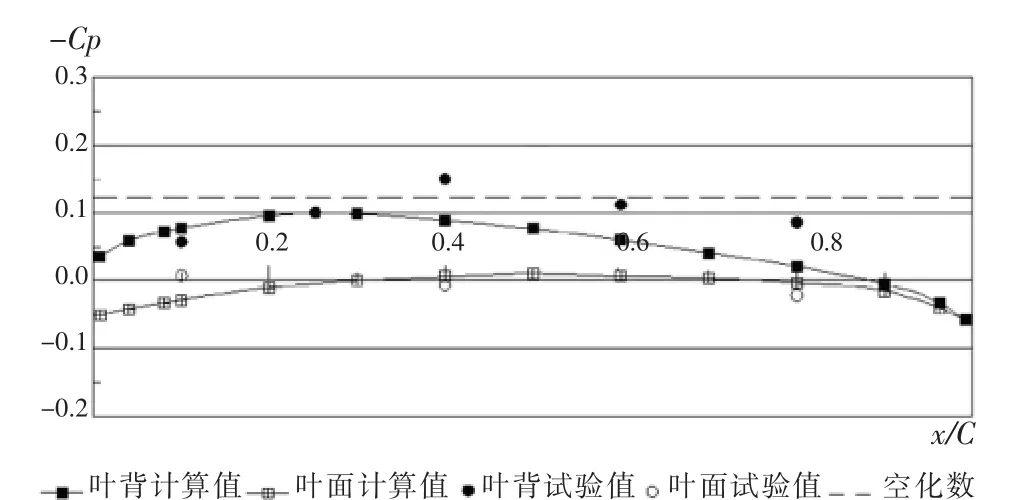
图7 HSP桨0.7半径剖面的非定场压力系数(90°)
图8为HSP桨0.7半径剖面的非定场压力系数(180°)。由图8可推断,桨叶转至此角度时,桨叶剖面在x/C=0.1~0.35处叶背开始产生空泡。
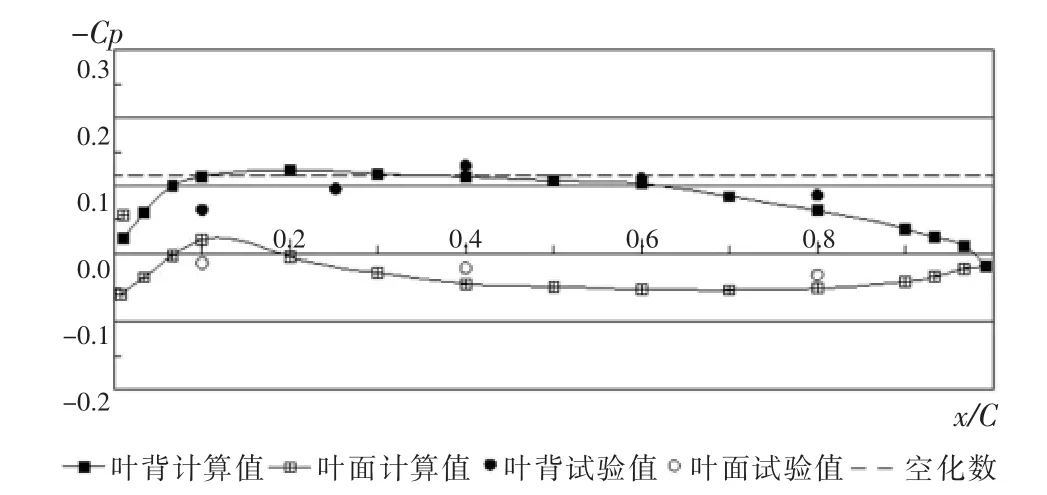
图8 HSP桨0.7半径剖面的非定场压力系数(180°)
图9为HSP桨在0.7半径剖面处的非定场压力系数(270°)。由图9可推断,桨叶转至此角度时,桨叶剖面不会产生空泡。
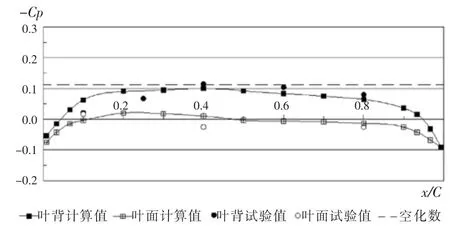
图9 HSP桨在0.7半径剖面的非定场压力系数(270°)
HSP 桨在 0.7 半径剖面、(0.25、0.4、0.6、0.8)弦长位置处旋转一周的压力变化如图10~图13所示。

图10 HSP桨在0.7半径剖面、0.25弦长位置旋转一周的压力变化(r/R=0.7,x/C=0.25)

图11 HSP桨在0.7半径剖面、0.4弦长位置旋转一周的压力变化 (r/R=0.7,x/C=0.4)

图12 HSP桨在0.7半径剖面、0.6弦长位置旋转一周的压力变化(r/R=0.7,x/C=0.6)
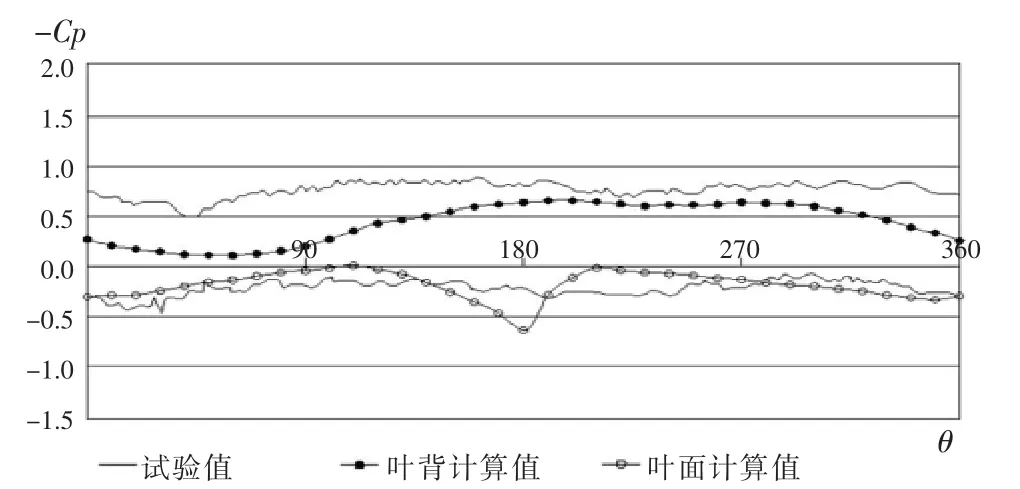
图13 HSP桨在0.7半径剖面、0.8弦长位置旋转一周的压力变化(r/R=0.7,x/C=0.8)
3 结 论
本文以第22届ITTC推进器技术委员会在1998年发布的HSP螺旋桨为算例,计算桨叶r/R=0.7处剖面在旋转至 0°、90°、180°、270°时的非定常压力系数,以及 r/R=0.7 处剖面在(0.25、0.4、0.6、0.8)弦长位置旋转一周的压力变化,并判断在各角度下是否会产生空泡以及空泡发生的位置。结果显示,计算值与实验值符合性较好,为螺旋桨设计者提供了一种可与螺旋桨升力线、升力面设计法相结合,初步判断桨叶剖面的空泡位置和空泡形态的方法。
[1]TERRYB.Mininum pressure envelopes for modified NACA-66 section with NACA a=0.8 camber and busfips typeⅡsection[J].Science.1965,148:12-64.
[2]黄汝道、陈才源.考虑来流速度场不均匀性影响的螺旋桨设计计算方法[J].舰船性能研究,1982(4):33-54.
[3]胡健.螺旋桨空泡性能及低噪声螺旋桨设计研究[D].哈尔滨:哈尔滨工程大学,2006.
[4]方会东.船舶螺旋桨空泡性能理论预报[D].哈尔滨:哈尔滨工程大学,2008.
[5]王超.螺旋桨水动力性能、空泡及噪声性能的数值预报研究[D].哈尔滨:哈尔滨工程大学,2010.
[6]王国强,董世汤.船舶螺旋桨理论与应用[M].哈尔滨:哈尔滨工程大学出版社,2005:235-313.
[7]王献孚.船用翼理论[M].北京:国防工业出版社,1998:50-57.
[8]刘岳元,冯铁城,刘应中.水动力学基础[M].上海:上海交通大学出版社,1990:230-247.
[9]JEFFERY J L著.张威,刘志军,李艳红,等译.数值分析与科学计算[M].北京:清华大学出版社,2008:441-443.

