基于数值试验的减振器阻抗特性研究

计 方 路晓东 王 锋 程 远

（1.中国舰船研究院 北京100192；2.哈尔滨工程大学 哈尔滨150001）

0 引 言

为抑制设备振动传递，通常在设备与基座之间安装减振器；为了保证安装施工最佳化，以获得艇体良好的声学性能，就必须掌握这些减振器的机械阻抗特性；为了使艇体低噪声化，提高安装质量并且对减振器安装前后的机械阻抗计算与测试就势在必行［1-3］。机械阻抗参数是进行系统隔振设计必要的原始参数，该参数无法通过解析法精确获得，并且，试验测试又需花费较大的人力与物力。因此，形成一套减振器机械阻抗数值计算方法，具有重要的工程应用价值［4-5］。

1 圆柱型橡胶减振器机械阻抗计算方法

隔振器的位移阻抗及速度阻抗定义为［6-7］：

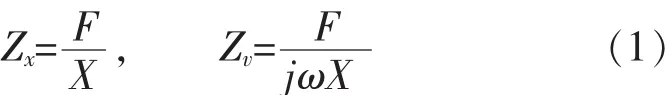
圆柱型橡胶元件通过四端参数法分析其机械阻抗特性。一般的隔振器在小振幅范围内，均满足线性定常系统的假设要求，因此，圆柱型橡胶元件可简化为图1所示的四端参数系统。

图1 圆柱型橡胶隔振器分析结构图

只考虑纵向稳态简谐振动时：

对于隔振元件单向振动，其两端动态力与振动速度关系可描述为：

式 中 ：Z11、Z22为 原点输 入阻抗 ，Z12、Z21为跨 点传递阻抗。

各阻抗参数由下列方程确定［8］：

对圆柱型橡胶减振元件，计及端部集中质量影响的阻抗矩阵可写为：

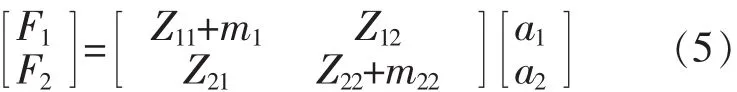
式中：m1、m2为端部金属体质量。

理想弹性元件为上面理想元件的组合体，其阻抗特性可以由理想元件的阻抗特性根据机械阻抗叠加原理综合得到。假设其输出端阻抗无穷大，输出加速度a2=0，其输入力和传递力有如下关系：

由此可得输入机械阻抗和传递阻抗的表达式：

图2 圆柱型橡胶隔振器原点机械阻抗

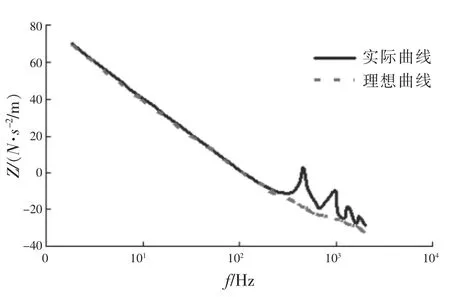
图3 圆柱型橡胶隔振器传递机械阻抗

图2、图3分别给出按理想弹性元件和实际弹性元件计算得到圆柱型橡胶隔振器的机械阻抗曲线。对比输入阻抗可以看出：理想弹性元件与实际弹性元件的阻抗值在低频段相吻合，而高频出现的波谷为橡胶体固有特性的耦合结果。当端部金属体质量与橡胶体质量相当时，耦合度较高，会使理想弹性元件与实际弹性元件的输入点阻抗在高频区的差异加大。

对比传递机械阻抗可以看出，在低频段两者计算结果吻合度较高，而高频段形成的上翘波峰是由橡胶体的固有特性（质量、刚度）造成的。在一系列峰值处，由于传递阻抗迅速增加导致隔振效果下降。

如上所述，理想弹性元件的阻抗对分析隔振系统低频特性是有效的，而减振器高频驻波效应导致隔振效果下降，传统分析方法不再适用。开展各型减振器阻抗特性数值试验和测量对全面分析由其构成的隔振系统特性十分必要。

2 典型减振器机械阻抗特性数值计算研究

2.1 E型减振器机械阻抗特性数值计算

E型减振器的实物图与某E型减振器的内部结构剖面视图，分别如图4、图5所示。

图4 E型减振器的实物图

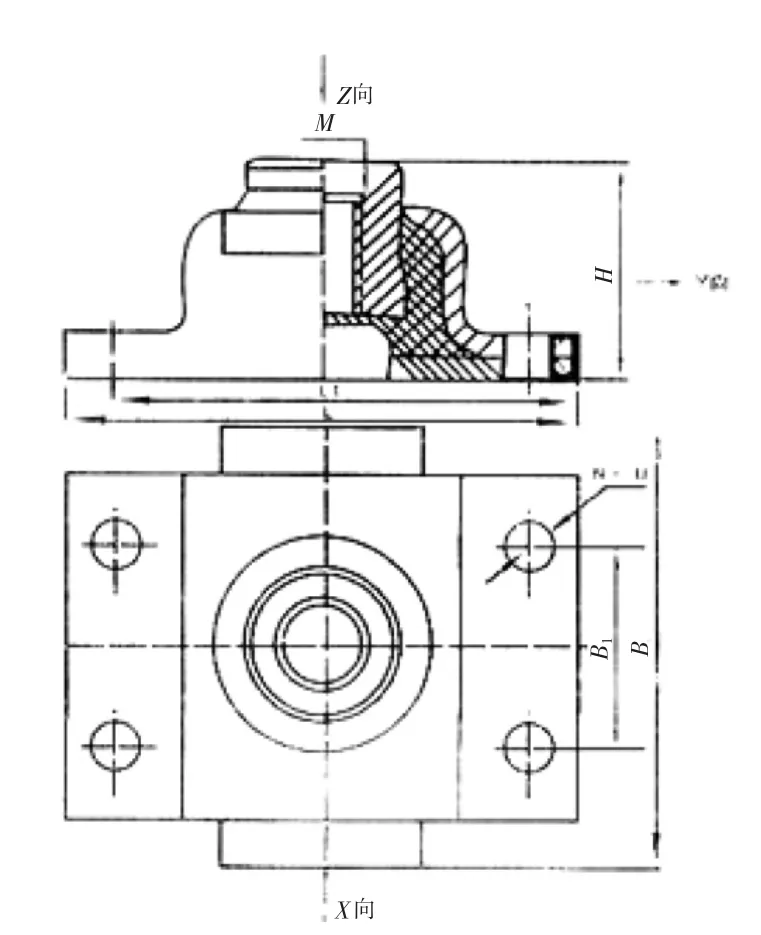
图5 某E型减振器内部结构剖面视图

本文采用实体单元构造一个接近于真实减振器的有限元模型，该模型不仅在形状上和实际结构相似，而且所有的几何参数和物理参数都是正确的，参见表 1、表 2。

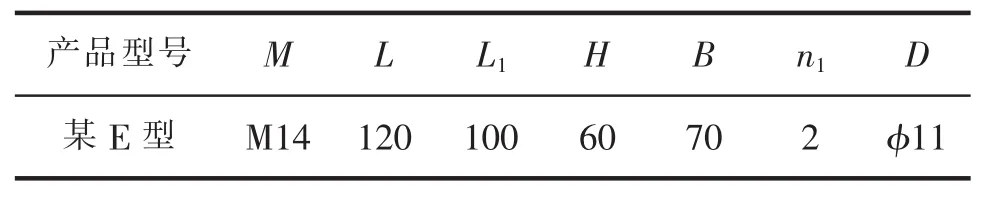
表1 某E型减振器结构参数

表2 某E型减振器技术参数

减振器模型在进行有限元网络划分时，其内部结构以及外表面均采用每个波长范围有5个节点的网络划分原则，以保证计算结果的准确性。为了使有限元的离散结构能更好地描述结构中的振动波传播，从波动理论出发，提出一个波长内至少应有5个节点（4个单元）。由此导出单元长度的细化标准，然后通过分析频率上限所对应的振动波波长来确定有限元网格划分的标准，参见图6～图10。

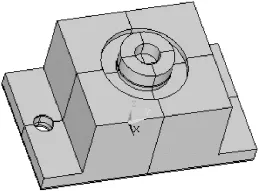
图6 某E型减振器有限元模型

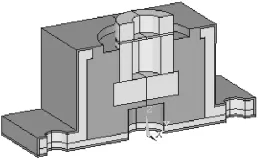
图7 某E型减振器橡胶及金属体有限元剖视图

图8 某E型减振器内部金属体有限元模型

图9 某E型减振器橡胶体有限元剖视图

图10 某E型减振器有限元网格视图

假设金属体的厚度为h=8 mm，材料弹性模量为E=2.1×1011N/m2，泊松比为 μ=0.3，材料密度为 7.8×103kg/m3，则波动理论导出的细化标准的过程如下：

金属体的纵长波波速

金属体中的弯曲波波速

当频率上限为1 000 Hz时，把相关参数代入上面公式得：

所以，本文的有限元单元划分，均应满足上述标准，即当频率上限为1 000 Hz时，单元尺寸应小于0.071 m。

边界条件的处理：数值试验模型与试验测试条件的边界条件保持一致，减振器有限元模型的底面刚性固定。

结构阻尼的处理：结构阻尼的大小对振动响应影响较大，特别是共振附近。由于阻尼的性质与大小往往不甚明确，阻尼的确定是相当复杂的，在很大程度上必须依赖于实际经验的积累。根据计算的频率范围，将结构阻尼系数取为0.02。

为了验证本报告有限元模型的准确性，通过有限元软件静力分析某E型减振器在Z向额定载荷下的静变形，满足公称要求。接着通过谐相应分析计算某E型减振器的原点及跨点机械阻抗，分别如图11、图12所示。

图11中，某E型减振器原点机械阻抗随着频率增加呈现缓慢递减趋势，在一阶共振频率处阻抗幅值达到最小值。随着频率继续增大，原点机械阻抗又呈现递增趋势。

图12中，某E型减振器传递机械阻抗曲线随着频率增加呈现单调递减趋势，在一阶共振频率后曲线变化趋势不明显。

图11 某E型减振器原点机械阻抗曲线

图12 某E型减振器传递机械阻抗曲线

2.2 BE型减振器机械阻抗特性数值计算

下面以某BE型减振器为研究对象 （见图13），通过合理的建模技术，借助有限元软件数值计算两型减振器的机械阻抗。

图13 BE型减振器的实物图

该BE型减振器结构参数与技术参数参见表3、表4。

表3 某BE型减振器结构参数

表4 某BE型减振器技术参数

该BE型减振器内部剖面视图如图14所示。

图14 BE型减振器内部结构剖面视图

图15～图17给出某BE型减振器的有限元模型。

图15 某BE型减振器有限元模型

图16 某BE型减振器橡胶及金属体剖视图

图17 某BE型减振器有限元网格视图

为了验证本报告有限元模型的准确性，通过有限元软件静力分析某BE型减振器在额定载荷下的静变形，满足公称要求；接着通过谐相应分析计算某BE型减振器的原点及跨点机械阻抗，如图18和图19所示。BE型减振器机械阻抗特性与E型减振器呈现相似的变化规律。某BE型减振器原点机械阻抗在共振频率处较某E型减振器显著增大。

图18 某BE型减振器原点机械阻抗曲线

图19 某BE型减振器传递机械阻抗曲线

3 加载对减振器机械阻抗特性的影响

根据国外有关文献可知，隔振器的动态特性参数受静载荷影响较大，特别是具有非线性特点的橡胶隔振器。因此，机械系统振动传递特性的预报应该使用加载状态隔振器阻抗的数值计算及测试结果。

将某BE型减振器额定载荷以质量的平均分配到减振器接触面的相应节点上，以质量点单元Mass21表示。

图20和图21分别给出了额定载荷下某BE型减振器的原点及传递机械阻抗曲线。

图20 额定载荷下BE型减振器原点机械阻抗曲线

图21 额定载荷下BE型减振器原点机械阻抗曲线

从某BE型隔振器的阻抗图谱可以看出，对于输入机械阻抗加载后一阶共振频率变小，在一阶共振频率以前阻抗幅值变小，一阶共振频率以后阻抗幅值变大；此外，传递机械阻抗加载后阻抗幅值变小。由于BE型隔振器属于剪切型隔振器，加载后橡胶部分同时承受拉伸和剪切，因此加载后刚度变小，最终导致一阶共振频率前其阻抗幅值变小，共振频率前移。

4 结 论

本文主要通过四端参数法理论分析了圆柱型橡胶减振器的阻抗特性。以E型和BE型减振器为研究对象，通过合理的建模技术，借助有限元软件数值计算得出如下主要结论：

（1）E型减振器原点机械阻抗随频率增加呈现缓慢递减趋势，在一阶共振频率处阻抗幅值达到最小值。随着频率继续增大，原点机械阻抗又呈现递增趋势。其传递机械阻抗曲线随着频率增加呈现单调递减趋势，在一阶共振频率后曲线趋于和缓。

（2）BE型减振器机械阻抗特性与E型减振器呈现相似的变化规律，BE型减振器原点机械阻抗在共振频率处较E型减振器显著增大。

（3）BE型减振器加载后共振频率前移，原点输入阻抗一阶共振频率前其阻抗幅值变小，一阶共振频率以后阻抗幅值变大。传递机械阻抗加载后阻抗幅值变小。可见，加载后橡胶部分承受拉伸和剪切，因而实际上是加载后刚度变小。

［1］左鹤声.机械阻抗方法与应用［M］.北京：机械工业出版社，1987.

［2］HARRIS C H，Crede C D，Shock and Vibration Handbook［M］.McGraw-Hill，1976.

［3］祝华，张宗安.弹性元件的机械阻抗理论研究［J］.噪声与振动控制，2001（4）：31-33.

［4］丁文镜.减振理论［M］.北京：清华大学出版社，1988.

［5］赵文礼，王林泽.机械振动设备随机疲劳和间隙非线性［M］.北京：科学出版社，2006.

［6］朱石坚，楼京俊，何其伟，等.振动理论与隔振技术［M］.北京：国防工业出版社，2005.

［7］王锁泉.Q702J4101-2004.隔振元件机械阻抗测试方法［S］.无锡，第七○二研究所企业标准.2004.

［8］王锁泉，周庆云，席亦农，等.隔振元件机械阻抗测量与数据处理方法研究［J］.2006，28（215）：107-111.