基于双重置乱技术的实数傅里叶变换域数字水印算法

沈 杨，于 军，吴兴波

(吉林化工学院信息控制与工程学院，吉林吉林132022)

随着数字媒体和网络技术的发展，媒体信息的数字化和网络化特征为信息的存取带来了方便，但是由于数字信息容易复制和传播，因此多媒体信息安全和版权保护问题已经成为社会的重要议题［1］.数字水印作为版权保护的一种有效途径，和对传统加密方法的有效补充手段，已经引起了人们的高度重视，成为多媒体信息处理领域的一个热点［2］.

数字水印算法主要有空间域法、变换域法、压缩域法、生理模型法和NEC法等［2］，因为变换域法具有算法操作相对复杂，但是透明性与安全性好，鲁棒性和抗攻击能力强等特点，所以自1996年首次出现变换域法以来，就以其优良特性受到广大学者的关注和欢迎.常用的变换域法有离散傅里叶变换(DFT)、离散余弦变换(DCT)、离散小波变换(DWT)等.

目前很多的变换域水印算法都是将水印图像置乱，然后把置乱后的水印嵌入到变换域载体图像的重要相关系数中(比如幅度谱或相位谱中)，一般水印算法都采取单一置乱的方法，如果置乱密钥被第三方获取，那么嵌入的水印就会被破解，信息安全就无从谈起.因此为了解决上述问题，文中提出了一种基于Arnold变换和采样置乱变换的实数傅里叶域双重置乱数字水印算法.双重置乱的应用，可以降低密钥被破译的风险.实验表明:该算法切实可行，具有一定的安全性、不可见和鲁棒性.

1 图像置乱

置乱技术［3］是一种图像加密技术.所谓“置乱”，就是将图像的信息次序打乱，将a像素移动到b像素的位置上，b像素移动到c像素的位置上，L，使其变换成杂乱无章、无明显意义的混乱图像，用于数字水印的预处理和后序处理过程.它可以很大的提高隐蔽载体的鲁棒性.置乱技术具有周期性，置乱变换后的图像大小不发生改变等特点.

双重置乱实际上就是对信息进行两次置乱(加密)，目的是使信息的安全性提高、隐蔽性增强，从而密钥被破解的难度加大.

1.1 采样置乱技术

采样置乱技术［3］是将图像分成大小相同的矩形或正方形小块，然后依序抽取其中的一个像素组合成新的图像块，最后按照某种排列方式拼成一幅新的图像.它有如下特点:采样过程不改变原图的直方图，像素只是发生位移;采样后形成原图的缩略图组合，随着迭代的进行逐渐形成能量分散的图像，当次数达到一定程度时又将向原图靠近.该算法置乱效果好，易于实现和恢复，通常只需要较少迭代次数即可达到分散的要求.经过试验发现，如果按照相同采样间隔其常见阶数的 图像采样变换周期［3］如表1所示:

表1 采样置乱周期

1.2 Arnold变换

定义［4］:设给定图像为:

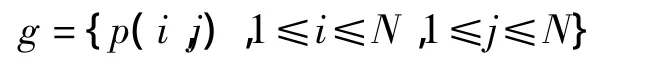
则其变换为:

其中p'为变换后的像素坐标，A为2×2的变换矩阵，且|A|=±1，并要求A中元素均为整数，当A，就是著名的Arnold变换，它实际是一种点的位置移动.这种变换是一一对应的，具有周期性，当迭代到某一步时，将重新得到原始图像.表2为置乱周期:

表2 Arnold 变换周期［4］

为了提高安全性，防止被非法用户解密，因此，我们采用双重加密，使解密难度加大.我们先要对图像进行采样置乱，再进行Arnold置乱.Arnold置乱次数为6，采样置乱次数为2.

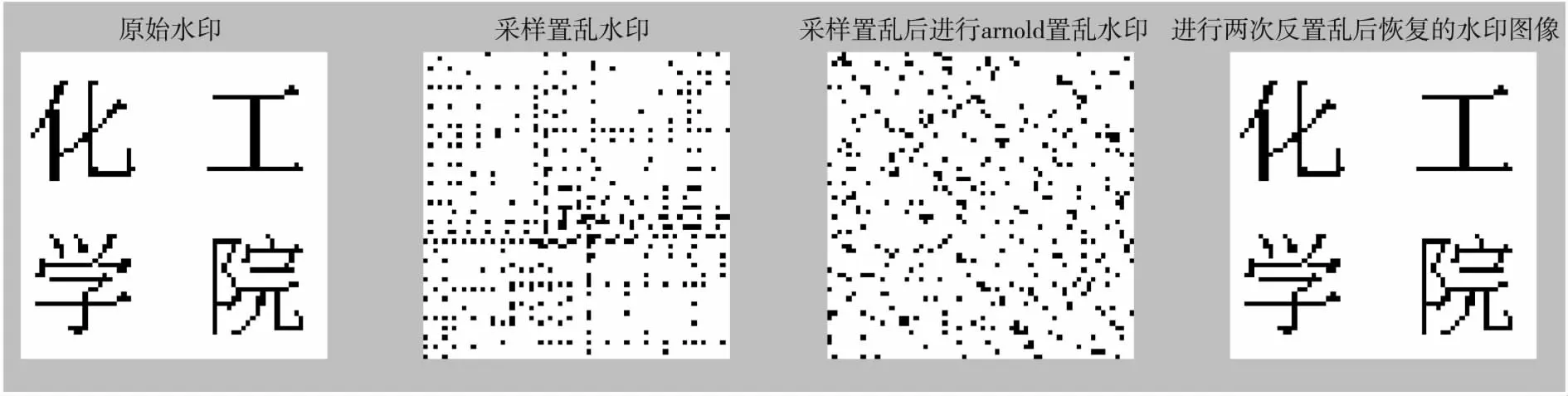
图1 为两种置乱相结合的实现效果图

2 实数傅里叶变换(RDFT)

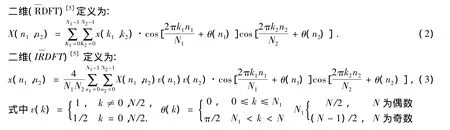
3 算法分析

3.1 水印嵌入算法

依据以上的嵌入理论，本文的水印嵌入算法流程框图:

图2 水印嵌入算法流程框图

水印嵌入算法步骤如下:

(1)将原始图像f(m，n)分成8×8的块.

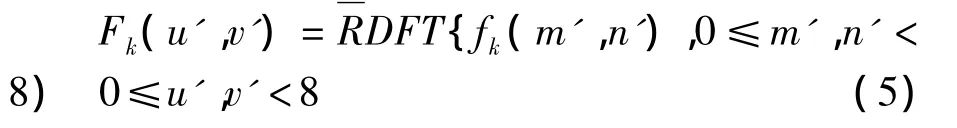
(3)利用采样置乱将二值水印进行置乱，再对置乱后的图像进行Arnold置乱.

(4)产生两个不相关的伪随机序列.

产生伪随机序列用MATLAB自带函数rand，并设定一个密钥key.密钥key用来产生特定的伪随机序列.只用使用相同的密钥key，嵌入水印和提取水印产生的伪随机序列才会完全相同.

(5)修改相应幅度谱值.

嵌入规则为当水印矩阵元素为‘0’时，将一个伪随机序列与幅度谱对应元素进行乘性叠加.当水印元素为‘1’时，用另一个伪随机序列与幅度谱对应元素进行乘性叠加.嵌入时以滤波矩阵选择嵌入块中的位置.

即:

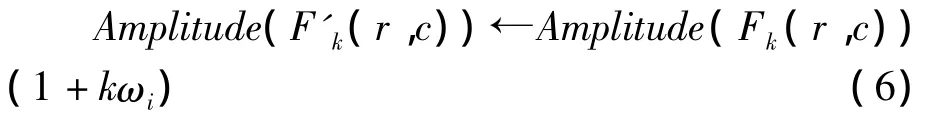
式中:Amplitude(·)为幅度，k为嵌入强度，ωi为随机序列.

嵌入时选取块(8×8)的中高频部分进行乘性叠加，尽量不破坏低频部分，因为低频部分是图像的重要部分，破坏会明显影响嵌入水印图像的不可感知性.

3.2 提取算法

水印的提取算法流程框图:

图3 水印提取算法流程框图

水印的提取步骤如下:

(1)对嵌入了水印的图像分成8×8块.

(3)产生两个不相关的伪随机序列.

使用与嵌入水印时相同的密钥key，即可产生两个与嵌入时相同的伪随机序列.

(4)计算嵌入水印相位谱与伪随机序列的相关性，当相位谱与第一个随机序列的相关系数大于幅度谱与第二个伪随机序列的相关系数，则取值为0，反之，取值为1.并将其值存入二值序列.

(5)将序列重构成二值图像，先进行Arnold反置乱后再进行反采样置乱对其进行恢复，得到水印图像.

4 实验结果

在Matlab7.0环境下仿真实验，载体图像为‘Lena’(256×256)，水印图像为‘化工学院’(32×32)，图2为载体图像和水印图像的，图3为嵌入水印的载体图像和提取的水印图像，嵌入置乱水印后图像的峰值信噪比PSNR=38.5230dB，相似度NC=0.9781.结果表明，嵌入置乱水印后图像与原始图像几乎没有区别，说明该水印算法具有较好的不可见性.

图4 原始图像和水印图像

图5 嵌入水印图像和提取水印图像

表3给出了嵌入水印图像在常规攻击情况下提取水印的测试结果.

表3 攻击实验检测结果

从表3中的结果可以看出，该算法对常规攻击如JPEG压缩、噪声和滤波等具有鲁棒性.

5 结 论

为了提高水印信息的安全性，使非法用户难以解密的目的，首先，提出了两种置乱技术相结合的方法，该方法实际上是双重加密，使解密的难度加大.然后，将加密后的水印信息嵌入到实数傅里叶变换域的中高频谱中.该方法不仅具有实数傅里叶变换的算法复杂度低、嵌入量大、计算高效等优点［6］，而且双重加密，解密困难的特点.实验结果表明，水印具有良好的鲁棒性和不可见性，能够较好的抵御各种常见的攻击.如JPEG压缩、噪声和滤波等.

［1］彭川，蒋天发.一种基于DCT的图像水印算法［J］.现代电子技术，2008，31(3):94-96.

［2］孙圣和，陆哲明，牛夏牧，等.数字水印技术及应用［M］.北京:科学出版社，2004:3-37.

［3］刘建华，李燕，张昌年.数字图像置乱技术及其Matlab实现［J］.桂林航空工业高等专科学校学报，2002，28(4):9-13.

［4］张华熊，仇佩亮.置乱技术在数字水印中的应用［J］.电路与系统学报，2001，6(3):32-36.

［5］辛怡，仲珏，陶然.基于实数离散傅里叶变换的图像数字水印算法［J］.兵工学报，2007，28(10):1261-1266.

［6］Ersoy O K.Real discrete fourier transform［J］.IEEE Trans Acoustics，Speech，Signal Processing.1985，ASSP-33(4):880-882.

［7］Ersoy O K，Hu N C.Fast algorithms for the real discrete fourier transforms［C］.IEEE ICASSP Conference.New York.1988，3:1902-1905.

［8］王卫卫，杨波，宋国乡.数字图像的一种相位水印算法［J］.西安公路交通大学学报，2001，21(2):37-39.

［9］Ingemar J Cox，Jee Kilian，Thomson Leighton F，et al.Secure Spread Spectrum Watermarking for Multimedia［J］.IEEE Transaction on Image Processing，1997，6(12):1673-1678.