多项式预测滤波技术在智能控制中的应用

董劲男1，邢千里1，班孝林2

（1.吉林大学计算机科学与技术学院，吉林长春 130012；2.深圳机场扩建工程指挥部，广东深圳 518000）

1 多项式预测滤波技术

1.1 理论依据及应用条件

信号预测技术一般可分为两类：随机信号预测方法和确定性信号预测方法。一般的噪声都是随机信号，它无法用数学关系式表达，只能用概率和数理统计的方法描述。目前常用的处理方法是采用一些相当成熟的线性预测方法，如牛顿型预测器。对于确定性信号预测也可以应用牛顿型预测器、FIR预测器、IIR预测器、神经网络预测器[1]和模糊系统预测器[2]等。

多项式预测滤波技术可以应用在平滑的实际信号采样处理过程中。将平滑信号建模为多项式信号模型并作为多项式预测滤波器的处理对象，是基于两点原因：首先，假定采样速率足够大，所有客观存在的信号会表现出类似分段多项式的特征；其次，基于多项式的信号处理计算效率高[3]。从定义上看，多项式预测滤波器能够估计类似多项式形式的信号的未来值。因此，对多项式预测滤波器的研究，其潜在应用涵盖了处理大量敏感度量的操作延迟和网络传输延迟，如：温度、位置、电压和功率等，尤其是在智能控制工程领域应用前景广泛。

1.2 无限脉冲响应（IIR）多项式预测器

通常来说，基于N个过去时刻的信号采样和M个过去预测器输出的向后p时步的IIR多项式预测器表达式如下[3]：

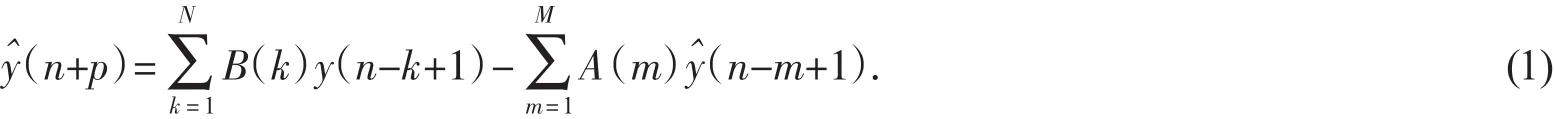
其中n为离散时间，B（k）和A（M）分别是IIR预测器的前向反馈和后向反馈的系数，y（n）是预测器输入信号，上标表示为估计值。其白噪声增益表示为：

其中H（ejω）=B（ejω）/[1+A（ejω）]为转换函数。需要指出的是，当舍去后向反馈部分，保留前向反馈部分，IIR预测滤波器就变换为我们下面将要介绍的FIR多项式预测滤波器。

1.3 有限脉冲响应（FIR）多项式预测器

有限脉冲响应是指单位脉冲响应函数为有限多项式，且输出只和前些时刻的输入有关系。有限脉冲响应（FIR）多项式预测器利用最近N（N为预测滤波器长度）个输入信号采样值外推未来时刻信号值。预测器的最小长度为M+1，当时N＞M+1，多余的自由次可以被用来最小化白噪声。其表达式为：

其白噪增益表示为：

利用多项式信号模型和公式(3)，并在公式(4)取最小值的约束下，利用拉格朗日乘子得到响应函数h(k)的推导公式：

当M＝1，p=1时

由推导公式(5)可以看出，滤波器的系数不依赖于输入信号，而是由N、M和p值决定的。同样的方法也可以用来构造FIR多项式微分器和正弦预测器，推导公式与多项式预测器类似。

FIR多项式滤波器可以看作是一个数据平滑滤波器的扩展[4]，使用低次多项式模型的FIR预测滤波器频率范围很窄，导致大多数的能量都集中在0频率附近。其缺点是旁带增益大，会干扰闭环控制；并且当滤波器长度很小的情况下，其止带增益非常大。为了缓解这种缺点带来的影响，可以使用面向特定应用设计的IIR低通滤波器。具体方法参见第三部分的相关论述。在实际应用中，多项式的次数I=0,1,2对于大多是信号的建模是足够的，高次的多项式预测器通常会出现高的旁带峰值增益和白噪声衰减差的现象，并且设计适用于高次多项式的幅度响应定形反馈难度很大[5]。

扩充型FIR预测滤波器[6]的基本思想是：用输入信号真实值和预测输入信号的加权和平滑输入信号，在预测的每一个时步内都将这种平滑后的信号值最为预测所用的信号值。优点是当预测器次数很小时仍能保证有效地减少旁带增益峰值并加强止带增益的衰减。

1.4 非线性自适应预测滤波器

当背景噪声是高斯噪声时，线性预测方法是最佳的。而对于非高斯噪声，Vijayan和Poor[7]提出了一种扩频通信抗窄带干扰抑制的非线性自适应预测滤波方法，用最小均方算法(LMS)和近似梯度算法更新滤波器的系数，能较好地预测窄带干扰信号，从而提高了系统的性能。张家树等[8]提出了一种非线性Laguerre自适应预测滤波器来抑制直扩频通信窄带干扰的方法。使用具有IIR和FIR滤波器特点的Laguerre时延单元取代非线性横向滤波器中的延迟单元z-1，构建了一种基于Laguerre横向结构的非线性自适应预测滤波器，既可以以较少参数模拟长脉冲响应，避免过参数估计问题，又可以保证收敛的稳定性。

2 应用

预测滤波器在设备控制领域和无线通讯领域都得到了广泛的应用。尤其是在汽车控制方面，预测滤波器能弥补传统光感脉冲编码器的精度问题[9-10]，允许设备在较小的采样速率下或者采样可能丢失的环境下实现高精度的状态检测，如速度、加速度和位移等；在无线通讯领域则体现在对CDMA闭环控制的补偿方面，通过预测可能的发送功率和接受功率，实现信道的充分利用，增加潜在的用户[3]。下面分类介绍多项式预测滤波器的应用。

2.1 速度测量

在车辆速度控制的研究中[11]，速度曲线可以近似为二次多项式。在高速的情况下，速度可以被高精度地估计出来。但在减速过程中，速度采样间的时间差分过大，超出了适用的采样周期，造成较大的预测误差。传统的传感器无法进行高精度的采样，且使用高精度传感器的成本过高。解决的方法是采用如下的预测控制策略：在采样值可用时，直接使用该采样值；当最新采样缺失时，则使用预测器预测出来的信号值。由此，预测器能够极大程度地弥补地精度传感器造成的控制偏差（图3）。

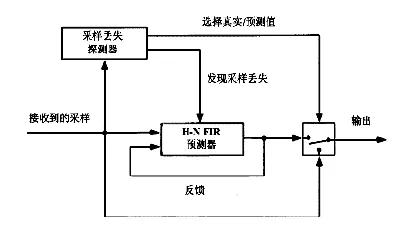
图3 速度采样预测器示意图

2.2 加速度测量

加速度在汽车控制中起到了很重要的作用，可以改善稳定机械系统的瞬时性能[12]和操控的强健性[13]。一般的加速度传感器过于昂贵，且在噪声环境下不稳定。利用向后差分器直接从速度信号求导得到的加速度信号[14-15]的准确度无法达到应用的需要，而采用数字微分滤波器虽然能够衰减噪声，但同时造成的延时破坏了系统的实时性[16]。解决的办法是引入一个由向后差分器、RLSN预测器[11]或预测FIR微分器[17]组成的级联。另外一种方法是首先使用递归微分器过滤速度信号，然后利用2个连续速度采样的差分得到加速度[18]。

2.3 控制延迟的补偿

计算处理时间延迟会破坏控制系统的性能，尤其是采样间隔小于时变计算延迟的时候，会导致采样的丢失。基于这个考量，引入附加的预测机制，使得控制闭环变得完整和可靠。例如：在文献[19]中，提出使用一个近似全通的滤波器预测补偿计算延迟；在医学信号处理和音频信号的恢复中使用均分滤波器和多项式预测滤波器[20]。

2.4 无线移动通讯系统中的应用

通过减少闭环发射器功率控制延迟可以增加移动CDMA通讯系统的用户容量[3,21]。假设无线通讯信道在一段时间是相互关联的，信道衰减变化记录可以用来预测信道的特性。使用预测滤波技术对可能接收到的功率级别进行估计，并确定闭环发射器功率控制系统的适度微调选择时机，可极大程度地改善信道的利用率，具体实现见图4。

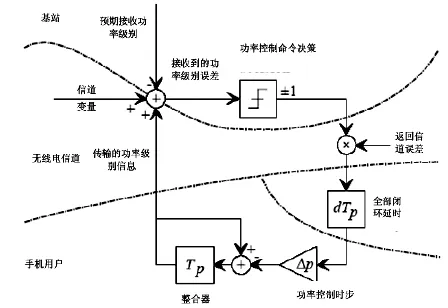
图4 多项式预测滤波器在CDMA通讯系统中的应用示意图

3 多项式预测滤波器存在的问题及改进方法

基于多项式的预测信号处理是一个众所周知的技术，但自身的缺点严重阻碍了其应用的推广：多项式预测滤波器对白噪声的衰减效果差，并表现出相当可观的滤波通带增益峰值。经过多年不断研究和改进，多项式预测滤波器的应用条件已经非常成熟，其中以使用面向特定应用的低通预滤波器的方法最为常用。

弱噪声衰减特性的改善可以通过两种途径：一种是引入一个由两个或两个以上滤波器（其原理同预滤波方法）或者多项式估计器和预测器组成的级联来改进[22-23]。另一种方法是在多项式滤波器中引入幅度响应定形反馈[6,17,24]，将可以改进噪声衰减特性的IIR滤波器扩展到FIR预测滤波器中，这种扩展保持了FIR预测滤波器的特性。在设计多项式预测滤波器时，定点表示给系数带来的影响必须要考虑，因为由此产生的舍入噪声[25]往往会破坏预测滤波器的适用条件。引入量化误差反馈能够很好地缓解由于算术计算量化产生的不良影响[26-27]。采用通用参数自适应机制[28]对FIR多项式系数进行适度微调[29]，扩大多项式FIR多项式预测器的适用范围。通用参数自适应机制是由加到每一个FIR预测滤波器系数并不断更新的简单参数实现的。

4 结论

多项式预测滤波技术发展已经相当成熟，并成功地应用到包括电子汽车控制、仪表控制和无线通讯网络等多个领域中。控制系统网络、传感器网络等一些新型的网络中传输的信息绝大部分是由传感器测取的（或是传到执行机构的）实时信号，其时间特性对用户至关重要。而网络环境的不确定性所造成的传输延迟和数据丢失等情况极大地制约了网络控制系统的发展。基于对预测滤波理论的研究和对多个成功应用实例的分析，将这种技术应用到网络控制系统的设计和分析中是可行的。

[1]B.Kosko,FuzzyEngineering,Upper Saddle River[M].NJ:Prentice-Hall,1997.

[2]Pekka Heinonen,YrjoNeuvo.FIR-Median Hybrid Filters with Predictive FIR Substructures[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1988,36(6):892-899.

[3]S.J.Ovaska,Newton-type predictors-Asignal processingoriented algorithmviewpoint[J].Signal Process,1991,25:251-257.

[4]P.T.Harju,S.J.Ovaska,Optimization ofIIR polynomial predictive filter magnitude response[J].Signal Processing,1997,56:219-232.

[5]Ovaska,SeppoJ,Olli Vainio,LaaksoTimoI.Design ofPredictive IIR Filters Via Feedback Extension ofFIR Forward Predictors[J].IEEE Transactions on Instrumentation and Measurement,1997,46(5):1196-1201.

[6]S.S.Rao.Optimization Theoryand Applications[M].2nd ed.NewDelhi,India:Wiley,1984.

[7]黄高勇,张家树.一种抑制直扩通信窄带干扰的新型非线性自适应预测滤波器[J].电子与信息学报,1999,29(6):1328-1331.

[8]Ovaska,SeppoJ.Improvingthe velocitysensingresolution ofpulse encoders byFIR prediction[J].IEEE Transactions on Instrumentation and Measurement,1991,40(3):657-658.

[9]刘清.考虑测量噪声的传感器动态测量误差补偿[J].江苏大学学报:自然科学版,2006,27(2):160-163.

[10]Sami Valiviita,Ovaska,SeppoJ.Delayless acceleration measurement method for elevator control[J].IEEE Transactions on Industrial Electronics,1998,45(2):364-366.

[11]Vainio,S.J.Ovaska.Tachometer signal smoothingwith analogdiscrete-time polynomial estimator[J].IEEE Trans.Ind.Electron.,1994,41:147-154.

[12]P.B.Schmidt and R.D.Lorenz,Design principles and implementation ofacceleration feedback toimprove performance ofdc drivers[J].IEEE Trans.Ind.Applicat.1992,28:594-599.

[13]G.P.Hancke and C.F.T.Viljoen.The microprocessor measurement oflowvalues ofrotational speed and acceleration[J].IEEE Trans.Instrum.Meas.,1990,39:1014-1017.

[14]H.Kadhim,T.K.M.Babu,and D.O’Kelly.Measurement ofsteadystate and transient load-angle,angular velocity,and acceleration usingan optical encoder[J].IEEE Trans.Instrum.Meas.,1992,41:486-489.

[15]Olli Vainio,Markku Renfors,TapioSaramaki.Recursive implementation ofFIR differentiators with optimumnoise attenuation[J].IEEE Instrumentation and Measurement TechnologyConference,1996(1):344-349.

[16]Sami Valiviita,Ovaska,SeppoJ.Delayless recursive differentiator with efficient noise attenuation for motion control applications[J].IECONProceedings(Industrial Electronics Conference),1998(3):1481-1486.

[17]S.J.Ovaska and O.Vainio.Predictive compensation oftime-varyingcomputingdelayon real-time control systems[J].IEEE Trans.Contr.Syst.Technol，1997,5:523-526.

[18]Vijayan R and Poor H V,Nonlinear technique for interference suppression in spread spectrumsystems[J].IEEE Trans.On Commun.,1990,38(7):1060-1065.

[19]T.Lipping,P.Loula,V.Jantti,and A.Yli-Hankala,DC-level detection ofburst-suppression EEG[J].Methods Inf.Med.1994,33:35-38.

[20]J.M.A.Tanskanen,A.Huang,T.I.Laakso,and S.J.Ovaska,Prediction ofreceived signal power in CDMAcellular systems[C].In Proc.45th IEEE Vehicular TechnologyConf.,Chicago,IL,1995:922-926.

[21]P.H ndel,P.Tichavsk,Asymptotic noise gain ofpolynomial predictors[J].Signal Processing,1997,62:247-250.

[22]J.A.Honkanen,T.I.Laakso,S.J.Ovaska.Lowpass IIR predictor for discrete-time signal processing[J].Digital Signal Process.,1995(5):133-139.

[23]L.B.Jackson.Digital Filters and Signal Processing:with MATLABexercises[M].Norwel,MA,USA:Kluwer Academic Publishers,1997.

[24]Sami Valiviita,SeppoJ.Ovaska,Olli Vainio.Polynomial Predictive Filteringin Control Instrumentation:AReview[J].IEEE Transactions on industrial electronics,1999,46(5):876-888.

[26]P.T.Harju,Roundoffnoise properties ofIIR polynomial predictive filters[C].In Proc.1997 IEEE Instrumentation and Measurement TechnologyConference,Ottawa,Canada,1997:66-71.

[27]J.M.A.Tanskanen and V.S.Dimitrov.Round-offError Free Fixed-Point Design ofPolynomial FIR Predictors and Predictive FIR Differentiators[J].Digital Signal Processing,AReviewJournal,2000(8).

[28]A.Ashimovand D.J.Syzdykov.Identification ofhigh dimensional systembythe general parameter method[C].In Preprints 8th Triennial World Congress ofIFAC,Vol.IV,Kyoto,Japan,1981:32-37.

[29]J.M.A.Tanskanen,O.Vainio,and S.J.Ovaska.Adaptive general parameter extension for tuningFIR predictors[C].In Proc.2nd IFACWorkshop on Linear Time DelaySystems,Ancona,Italy,Sept.2000:42-47.

[30]J.G.Proakis,D.G.Manolakis.Digital Signal Processing:Principles,Algorithms,and Applications[M].NewYork,NY,USA:Macmillan PublishingCompany,1992.