例题选择要以生为本

☉江苏省如皋市江安镇滨江初级中学 周文斌

复习课，有别于新授课，没有固定的教材，一切都要重新开始．所以，对于初中数学复习课而言，例题的确定成为教师首先要解决的问题．近期听了多节复习课，感受最深的莫过于不同教者在例题选择上的差异．尤其是少数老师选题用题非常随意，导致课堂教学成效低下，严重影响复习课的质量．本文就选择其中几个案例加以分析，以期能引起广大数学老师的共鸣．

一、选题“误区”

1.偏离教学目标

案例一：“二次函数”复习.

在九年级“二次函数”复习课上，一位老师选择了如下的例题：

（1）求抛物线的解析式及顶点D的坐标；

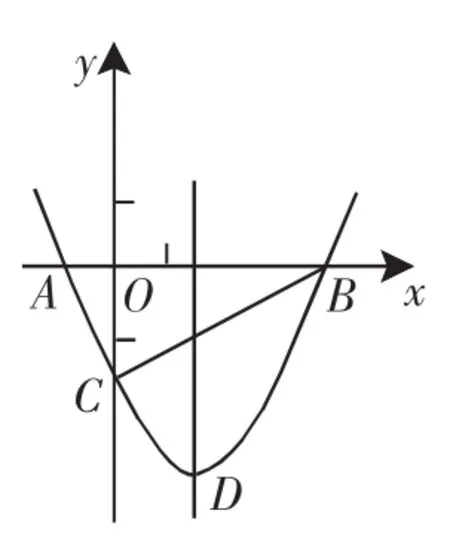
图1

（2）判断△ABC的形状，证明你的结论；

（3）点M（m，0）是x轴上的一个动点，当CM+DM的值最小时，求m的值.

案例分析：这是2011年贵州省安顺市的中考第27题，该题作为中考第一轮复习的例题，很明显，偏离了本课的教学目标.问题（1）回顾了“二次函数”复习中的一个教学目标“会用待定系数法求二次函数的解析式”，而问题（2）、（3）所涉及的直角三角形的判定、轴对称的性质和一次函数的图像等知识与本课的教学目标没有太多的关联，而且解决后两问非常耗时.显然，这样的选题是失败的.

2.忽视学生认知基础

案例二：“全等三角形”复习.

在“全等三角形”复习课上，八年级一位老师选择了这样一道例题：

例2 （1）如图2所示，在正方形ABCD中，M是BC边（不含端点B，C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点.若∠AMN=90°，求证AM=MN.

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明.

证明：在边AB上截取AE=MC，连接ME.在正方形ABCD中，∠B=∠BCD=90°，所以∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB.

下面请你完成余下的证明过程.

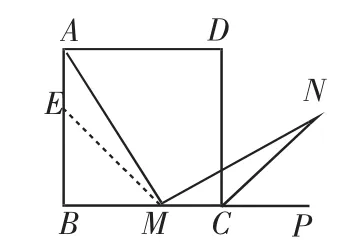
图2

图3

（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图3所示），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由.

（3）若将（1）中的“正方形ABCD”改为“正n边形ABCD…X”，请你作出猜想：当∠AMN=______时，结论AM=MN仍然成立.（直接写出答案，不需要证明）

案例分析：虽然学生在小学中对正方形、正三角形、等腰三角形等相关知识有所了解，但在初中数学教材中，真正系统研究这些图形的性质均在“全等三角形”之后.教者之所以选择这道题目作为例题，无非有这样几种可能：一是“错误”地认为学生对这些图形的认知已经达到“运用”的程度；还可能就是根本没有弄清教材的编排；也不排除这位老师有“人为拔高”教学目标的可能.但无论是其中的哪一种，这位老师一定没有好好研究学生、教材和课标，对学生认知缺乏起码的“尊重”.

3.容量大，难度深

案例三：“特殊的平行四边形”复习.

在中考第一轮复习“特殊的平行四边形”时，一位老师选择了下面的题目作为本节课的例题：

例3 如图4，平面内4条直线l1、l2、l3、l4是一组平行线，相邻两条平行线间的距离都是1个单位长度，正方形ABCD的4个顶点A、B、C、D都在这些平行线上，其中点A、C分别在直线l1和l4上，该正方形的面积是______平方单位．

图4

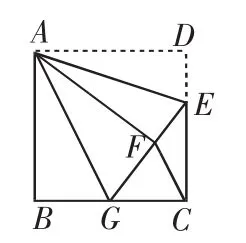
图5

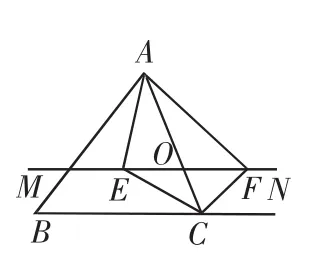
图6

例4 如图5，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG＝GC；③AG∥CF；④S△FGC＝3．其中正确结论的个数是（ ）.

A．1 B．2 C．3 D．4

例5 如图6，在△ABC中，点O是AC边上（端点除外）的一个动点，过点O作直线MN∥BC.设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，连接AE、AF．那么当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

例6 已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O.

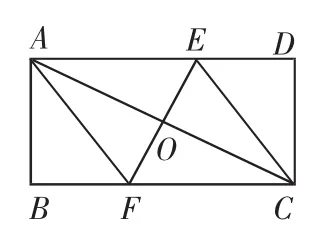
图7

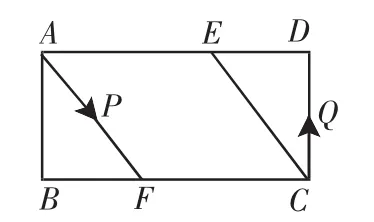
图8

（1）如图7，连接AF、CE.求证四边形AFCE为菱形，并求AF的长.

（2）如图8，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止，点Q自C→D→E→C停止.

在运动过程中，①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值.

②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式.

案例分析：笔者认为，将这么多经典的考题简单堆砌以例题的形式呈现，是不妥的．首先，学生无法在规定时间内完成这些例题的解答，例题分析和方法归纳也就会比较草率，事实也的确如此；其次，例题难度太大，“受益面”狭小，除例5外，其他三道例题都处于中考试卷中的相同题型的“压轴题”位置，要知道并不是每一位同学都能达到这样的高度的；最后，例题涉及的知识点太多，不能够突出本课的复习重点“特殊平行四边形的性质和判定方法”．

二、三点建议

1．选题要摸清学情与教学目标，确保有的放矢

学情，即学生的情况，包括学生的认知基础、学习习惯、学习方法等，摸清学情是保证教师高效教学的前提．摸清学情应该包括弄清学生会了什么，什么没会，学习习惯如何，解题速度怎样等．只有将这些情况弄得一清二楚，才能让我们的选题接“地气”，紧贴学生．当然，我们的选题也决不能偏离当堂课的教学目标．作为老师，我们不能不考虑单位时间的教学效益，一节课该做什么，能做什么，做到什么程度，在选题前就应该心中有数．决不能像案例一中的老师那样“捡了芝麻丢了西瓜”，将课堂中最宝贵的时间花在了与本课关系不大的例题上．如果说弄清学情和教学目标是初中数学老师选题前的“必做功课”，那么尊重学情和教学目标应该成为选题的“底线”．

2．选题必须讲求实效，根据需要进行合理取舍

选择例题必须追求实效，但追求实效，绝不是求多，贪深．“让每一道例题都卓有成效”应该成为每一位初中数学老师选题时的追求，要让出现在课堂中的每一道例题，都有明确的指向，为本课的教学目标服务．追求实效主要体现在：（1）选题要大度，敢于取舍；（2）不盲从教辅，敢于质疑；（3）勤于“下水”，感知“深浅”．

在复习“概率初步”时，笔者初选了南通市2011年的中考第25题作为例题．

例7 光明中学十分重视中学生的用眼卫生，并定期进行视力检测．某次检测设有A、B两处检测点，甲、乙、丙三名学生各自随机选择其中的一处检测视力．

（1）求甲、乙、丙三名学生在同一处检测视力的概率；

（2）求甲、乙、丙三名学生中至少有两人在B处检测视力的概率．

在亲自“下水”解答后，发现原题中的两个问题的解决途径是一样的，如果让学生全部求解，无形中浪费了宝贵的教学时间．为此，笔者直接删去了原题中的第一问．显然，案例一中的老师完全可以删去原题的后两问．

3．选题要体现“层”和“度”，让每一位学生都学有所获

例题的“层”和“度”是在选题时必须考虑的，究其原因有三：（1）学生的数学认知是有差别的，不可能在同一知识上同时达到相同的高度；（2）教师必须处理好“吃得饱”和“吃得了”之间的关系；（3）为学生营造愉快的解题环境是数学老师的职责．以案例三为例，我们可以将前面两题调整为两道简单点的例题，同时提出“例3—例5必做，例6选做”的要求．这样一来从题目的“梯度”上体现了例题的“层”和“度”，在让部分基础薄弱学生“吃得了”的同时，又为相对优秀学生解答例6赢得了不少时间，让他们能有时间去“吃饱”．体现例题的“层”与“度”，除了设置“必做题”与“选做题”外，还可以分级别选择例题．要想自己不处于案例三中“遍地开花，鲜有结果”的尴尬境地，我们就应该用更多的精力去分析到每一个学生和每一个知识点．

课堂是“圣地”，选题要谨慎．选题，是一门学问．对于初中数学老师而言，认真研究选题显得尤为重要．面对众多的中考题，有时真就无所适从，一不注意就“迷了眼”，盲从于这些考题．只有树立“以生为本”的理念，让选题贴生进行，才能真正打造出高效的复习课堂.

以上仅是笔者在听课过程中的所见、所闻及所想，希望能对您有所启示，更期待着众多的专家同行能将自己的选题建议与好的方法分享，本文权当引玉之砖吧！