理解概念 明确法则 熟练应用——苏科版七年级“2.4相反数”解读及教学实录片段

☉江苏省苏州中学园区校 耿恒考（特级教师）

对于“相反”一词，学生有初步认识，如“2.1正数与负数”中学习的“具有相反意义的量”.在学生的头脑中，只有方向相反、意义相反或者符号相反等概念，但对于“互为相反数”还是比较陌生的.

课程标准要求“借助数轴理解相反数的意义，掌握求有理数的相反数的方法”.借助数轴可以直观感受到有理数（正数、0、负数）的相反数的意义，体会相反数与绝对值的密切联系.根据七年级学生的知识、能力，确定本课时的教学目标为：

（1）借助数轴理解相反数的概念；

（2）会求一个数的相反数，会用相反数的意义进行化简；

（3）通过对相反数的意义和求一个数相反数的方法的探究，培养学生观察、比较、分析、归纳、概括的能力，体会数形结合思想，感受数学与生活的联系.

教学重点：理解相反数的意义，熟练地求一个数的相反数；教学难点：感受互为相反数的几何意义，体会数形结合思想.

值得注意的是：“相反数”不是一个数，而是两个数之间的一种特殊关系.“理解概念，明确法则，熟练应用”是学好本课内容的关键.

理解概念：（1）要让学生懂得何为互为相反数，明确互为相反数的两个要素：符号相反及绝对值相等；（2）知道表示互为相反数的两个点在数轴上的位置特征，即除0以外，表示互为相反数的点在原点的两旁，且到原点的距离相等；（3）相反数与绝对值有着密切联系，绝对值等于0的数一定是0，绝对值为正数m的数一共有两个，分别是m、-m，是一对互为相反数，互为相反数的两个数绝对值相等.

明确法则：要让学生感悟到表示一个数的相反数就是在这个数前面添一个负号，即a的相反数为-a.正数的相反数是负数，负数的相反数是正数，0的相反数仍然等于0本身.

一、教学设计思路

1.情境设计

（1）相反数的概念.

设计方案1：①请两名同学在讲台桌前背靠背站好，听口令“向前4步走”.②规定向右为正（正号可以省略），向右走4步，向左走4步各记作什么？（向右走4步记作4步；向左走4步记作-4步）③规定两名同学的出发点为原点，用上一节课学的数轴将上述问题情境中的4和-4表示出来.④从数轴上观察，这两名同学走的距离都是4步，但方向相反，可用4和-4表示，这两个数具有什么样的关系？⑤教师引导，让学生从方向和大小两方面归纳总结定义.

设计方案2：①请一名学生到台前，在黑板上画出的的数轴上标出表示-5和5、-1.5和1.5的点（其他学生在本子上画）；②观察数轴上表示-5和5、-1.5和1.5的点的位置有什么特点？③教师点拨引导，让学生通过观察两点的位置及它们与原点的距离发现规律，归纳总结出相反数的定义.

设计意图：方案1通过设计生动有趣的情景，引导学生借助数轴的直观性，吸引学生的注意力，激发学生的学习兴趣.学生在老师的引导下将实际问题数学化，体会出4和-4这两个数互为相反的意义，感受数学与生活的密切关系，在轻松愉悦的活动中获得了知识，从感性上初步感知互为相反数的意义.方案2的设计既复习了数轴的知识，又开门见山，使学生动手、动脑，参与到教学活动中来，“由形到数”将直观问题数学化，感受“数形结合”的数学思想.其目的是培养学生动手做数学的能力，不断积累数学经验.

（2）相反数的认识.

设计方案1（游戏：快速问答）：一名学生说出一个数，然后指定另一名学生回答它的相反数，两人再交换出题，比一比看谁回答得又快又好.

设计意图：方案1通过生生互动，寓学于乐，充分利用学生的好胜心理，既促进学生之间相互交流、相互评价、相互补充的合作氛围，又能激发他们的竞争意识.方案2寓教于乐，让学生在游戏中进一步体会相反数的意义，突出对0的相反数仍然是0的理解.实现难点的突破，提高学生的学习兴趣.

2.探究活动

（4）说出下列各数的意义：①-（+15）；②+（-7.2）；③-（-32）；④+（+5.7）.

设计意图：问题（1）让学生直观感悟相反数的特征，巩固对相反数的理解.问题（2）通过画图观察，让学生感悟：除0以外，表示互为相反数的点在原点的两侧，且到原点的距离相等.体会相反数的两个要素：符号相反及绝对值相等.问题（3）分别求无理数、整数、分数、小数、0的相反数，加深学生对相反数概念的认识与理解.引导学生总结，通常在一个数的前面添上“-”，就表示这个数的相反数，而在一个数前面添上一个“+”,即表示这个数本身.说明求一个数的相反数就是在这个数前面添上一个“-”.问题（4）通过对正号和负号不同组合的认识，总结符号化简的规律，感悟正数的相反数是负数，负数的相反数是正数；一个数前面添加“+”，仍等于这个数本身.

3.例题教学

例1 填空题：

①-（-2）是______的相反数，-（-3.14）的相反数是______

②-a的相反数是______，-a的相反数是-9，则a=______.

③数轴上到原点距离为5的点表示的数是______.

例3 化简：①-（+20）；②+（-2.5）；③-（-13）；

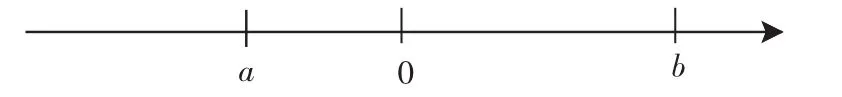
图1

设计意图：例1中设计几个填空题，旨在进一步让学生清楚对相反数意义的认识，直观感受相反数的几何意义.例2通过求不同类型的有理数的相反数，使学生进一步清楚如何求一个数的相反数.通过示范，防止学生将-4.5的相反数误写为：-4.5=4.5.通过例3的学习，既强化对符号化简规律的理解，明确正数的相反数是负数，负数的相反数是正数，又能让学生清楚区分括号与绝对值的不同.例4既巩固对绝对值、相反数意义的理解，又强化“数形结合”思想在解题中的应用，为下一阶段学习用字母表示数、代数式等知识作铺垫.

4.尝试练习

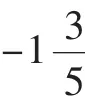
（2）如果a=-6，那么-a=______；如果-（2a）=6，那么-a=______.

（3）已知有理数a与b互为相反数，则a与b应满足的关系式为____________.

（4）_____数的相反数比它本身大，_____数的相反数比它本身小，_____的相反数和它本身相等.

（5）数轴上与原点的距离为4.5个单位长度的点所表示的数是_____.

（6）化简：-（+6）=____，-（-1.3）=____，-［+（-3）］=____.

（8）有理数a、b在数轴上的对应点如图2所示.请在数轴上标出表示-a、-b的点；并把a、b、0、-a、-b五个数用“＜”连接起来为_____________.

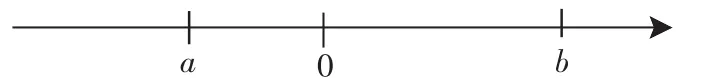
图2

设计意图：设计以上几个练习，旨在巩固并检测同学们对所学新知识的掌握情况，以便及时进行反馈矫正.

二、课堂教学片段实录

1.情境导入

师：请两位同学上来做一个表演“背道而驰”，谁愿意参与？

（同学们争着举手，积极主动.老师选生1、生2在讲台桌前背靠背站好）

师：请同学们注意观察、思考、发现.听口令：“向前4步走”.

师：规定向右为正，向右走4步，向左走4步各记作什么？

生3：向右走4步记作“4步”或“+4步”；向左走4步记作“-4步”.

师：如果规定两个同学的出发点均为原点，你能用上一节课学的数轴将上述问题情境中的4和-4表示出来吗？哪位同学愿意到前面来展示？

（生4在黑板上画数轴，并标出表示4和-4的点）

师：从数轴上观察，这两位同学走的路程都是4步，但方向相反，可用4、-4来表示，这两个数具有什么样的关系呢？

生5：4和-4这两个数具有相反意义.

师：回答的很好.还有同学要说吗？

生6：4和-4的数字相同（都是4），但一个是正的、一个是负的，性质符号不同.

生7：表示-4和4这两个数的点在数轴的两边，距原点都是4个单位长度.

师：在数学中，把具有上述特点的两个数称为互为相反数，今天我们就来研究相反数.（教师板书课题“2.4相反数”，板书互为相反数的定义）

2.探究新知

（1）互为相反数的意义.

师：请同学们在数轴上标出-3、1、5及它们的相反数的对应点.感受互为相反数的几何意义.

生8：-3、1、5的相反数分别是3、-1、-5.

图3

师：你能在数轴上把它们的对应点标出来吗？试试看.

（生8展示后（如图3），教师再添加如图4所示的几条线段，标识单位长度）

图4

师：请同学们谈谈互为相反数在数轴上的对应点的特征.

生9：这些点在数轴上的位置特征分别是：①在原点的两侧；②到原点的距离相等；③关于原点对称.

生3：在数轴上与原点距离相等的点都有2个.表示的数分别是：1和-1，-3和3，5和-5.

生2：不一定对吧？0呢？0和0是互为相反数，但是它们在数轴上对应同一个点，即原点.

生9：对！0是特殊的，0除外.

师：大家的观察能力、归纳能力真不错！总结的非常好.表示互为相反数的两个点在数轴的位置，在原点的两侧，且到原点的距离相等.当然0除外（0的对应点还是它本身）.

师：我们一起来做个游戏“快速抢答”，比比看，谁最棒！

游戏“快速问答”：一名学生说出一个数，然后指定另一名学生回答它的相反数，两人再交换出题.比一比看哪组回答得又快又好.

比赛形式：①随机抽两个小组竞赛，②10名男生和10名女生竞赛，问和答交换.

师：通过刚才的小游戏，请同学们谈谈对互为相反数的认识？

生10：正数的相反数是负数，负数的相反数是正数.

生11：0的相反数是0本身.互为相反数的绝对值相等.

生7：绝对值相等的两个数，它们相等或互为相反数.

生12：相反数表示的是两个数的关系，不是单独一个数.

师：同学们都不错，回答的很好，哪位同学能将刚才各位同学谈的对相反数的认识概括一下？准备一下，你能行！

生10：正数的相反数是负数，负数的相反数是正数，相反数等于本身的数只有0；表示一个数的相反数就是在这个数前面添一个负号，即a的相反数为-a.

师：非常好，很准确.同学们再考虑，互为相反数的和为多少？商为多少（0除外）？

生：都惊讶！啊，对哦！互为相反数的和为0、商为-1（0除外）.

（教师总结归纳，并板书要点）

师：你能说出下列各数的意义吗？

①-（+20）；②+（-2.5）；③-（-13）；④+（+7）.

生13：20的相反数、-2.5本身、-13的相反数、就是7.

生14：我觉得这里面有规律，正正得正，负负得正，负正、正负都得负.

生8：我觉得你说得不好，不如看前面的负号的个数，有奇数个负号为负，有偶数个负号为正.

师：大家感觉怎么样？你同意他俩的观点吗？

生齐说：同意！

师：他们总结的确实不错，很好！我举双手赞成！

（2）例题教学.

例1 填空题：

①-（-2） 是______的相反数；-（-3.14） 的相反数是______.

②-a的相反数是______；-a的相反数是-9，则a=______.

③数轴上到原点距离为5的点表示的数是______.

（学生思考2分钟，举手回答）

生15：①中-（-2）就是-2的相反数，也可理解-（-2）就是2，它是-2的相反数；-（-3.14）等于3.14，它的相反数是-3.14.②中应该填a、-9；③中应该填5.

生9：③不对，应该是5和-5，因为数轴上到原点距离为5的点有两个，分别在原点的两边，即为5和-5.

师：是的，同学们要特别注意：“到原点距离为5的点表示的数”就是“绝对值等于5的数”，而绝对值等于5的数有两个，它们是一对互为相反数，即-5、5.

（待同学思考2分钟后，请一位同学到黑板上写出来）

师：她做得对吗？

生齐答：对，没问题.

师：如果将它们分开写呢？“12的相反数”写成12=-12，对吗？为什么？

生齐声说：不对，不对.

师：该怎么写？

生17：12的相反数是-12.

师：是的.“12=-12”，这是矛盾的.无法用这样的式子表示，而要用语言表达.

（学生思考2分钟后，教师安排四位同学到前面板演）

师：他们做得怎么样？对吗？

师：对.我们要清楚区分括号和绝对值的不同.

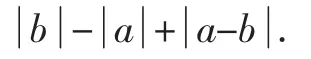
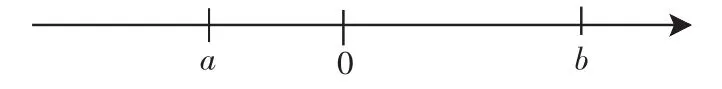
图5

师：同学们，谁能说说绝对值的意义？

生19：正数和0的绝对值等于它本身，负数的绝对值等于它的相反数.

师：好，同学们讨论得很热烈.哪个小组能解决，请派代表发言.

第五组生16：要知道数b、a、a-b是正的还是负的才行.

第三组生12：根据数轴可以看出b＞0、a＜0、a-b＜0，因此原式=b+a+b-a=2b.

3.反思与小结

师：通过这节课的学习，你有哪些收获？还有什么困惑需要大家帮助解决吗？

（许多同学都在争着谈自己的收获，谈对相反数的意义的理解和如何求一个数的相反数）

生20：老师，如果一个数前面有多重括号，如：-{-［+（-2）］}，该怎么化简啊？

师：问得好，哪位同学能帮助解决？

生18：这题化简的结果是-2.其实我们只要看2前面的“-”的个数，若有奇数个，结果为负；若有偶数个，结果为正.

师：是的，这样考虑可以.还可以有别的考虑方法吗？

生6：我是从里向外逐层化简的，或者从外到内也可以的.

师：你赞成她的观点吗？

生齐声说：赞成！

师：很好，刚才两位同学提供了两种解决问题的方法，都是可行的.你理解了吗？

生20：懂了，谢谢！

师：同学们还有问题吗？

生齐声说：没有！

师：好的.今天我们共同探讨了互为相反数、如何求互为相反数，相信大家有这样的学习热情、探究问题的能力，将来一定都会有很大成就的！

三、教学感悟

学生是学习的主体，教师不仅要授之以鱼，更应该授之以渔.教师要以教学生如何观察、分析、解决问题为突破口，以让学生形成积极探求新知的欲望为情感目标，教给学生探究问题的方法，培养学生良好的数学素养和学习习惯.发展学生的能力，需要设计出层层递进的“问题链”，“问题是数学的心脏”，用问题激活学生的思维，用问题推进教学进程，用问题引导学生探究.

本节课堂教学活动中的问题，都是在教师的引导下由学生观察、思考、讨论解决的，如“互为相反数的意义”“例题教学”“课堂感悟与小结”等的教学活动.学生能解决的问题，应尽量由学生们来解答、补充、评价、完善，最终实现问题的解决，这样学生的学习能力不断得到锻炼和提升.只有全班同学都解决不了的问题才由教师来解决，这样教师就退到了最后一道防线，教师只是精讲点拨.课堂上教师就是“望梅止渴”里的“梅”，教师要力争达到“一般不出场，出场不一般”的效果.教师在课堂上更多的是组织、引导学生学习，教师的作用就是调动学生的学习积极性和激发学生学习的内驱力，让每个学生都成为“动车”而不是“拖车”，使我们的课堂不仅实现“学生动起来，课堂活起来”，更能达到“效果好起来”.