用线性插值公式证明一类高考题

☉江苏省启东市汇龙中学 朱健忠

题目：1.（2009年湖北文）过抛物线y2=2px（p＞0）的焦点F的直线与抛物线相交于M，N两点，自M，N向准线l作垂线，垂足分别为M1，N1.记△FMM1、△FM1N1、△FNN1的面积分别为S1、S2、S3，试判断4S1S3是否成立，并证明你的结论.

2.（2009年湖北理）过抛物线y2=2px（p＞0）的对称轴上一点A（a，0）（a＞0）的直线与抛物线相交于M，N两点，自M，N向准线l：x=-a作垂线，垂足分别为M1，N1.记△FMM1、△FM1N1、△FNN1的面积分别为S1、S2、S3，是否存在实数λ，使得对任意的a＞0，都有S22=λS1S3成立.若存在，求出λ的值；若不存在，说明理由.

为了节省篇幅，直接将上面两题一般化或类比到椭圆与双曲线，有下面两个结论：

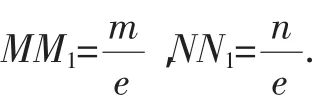
上面两个性质都是圆锥曲线共有的性质，性质1突出过焦点作直线，而性质2将条件进一步放宽.证明它们的方法比较多，可以用解析法，也可以用平面几何法.笔者仔细研究后，觉得性质1用线性插值公式证明显得十分简单.而性质2只需适当转化，可迅速转化为性质1的证明方法.

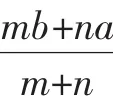
证明：如图1，连接AC交EF于G，由AD∥EF∥BC得：

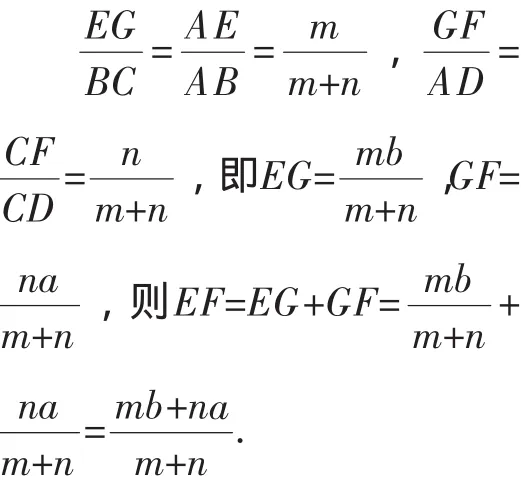
说明：（1）当E，F在AB，DC延长线上时，m∶n为有向线段AE，EB的数量比，才能使公式成立；

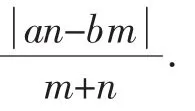
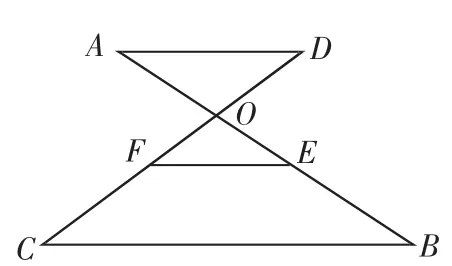
图2

下面给出性质1的证明.

证明：如图3，若圆锥曲线C为抛物线、椭圆或双曲线且M、N在同一支上时：

设过焦点F的直线交圆锥曲线于M、N，自M、N向相应准线作垂线，垂足分别为M1、N1，FM=m，FN=n，∠FMM1=θ，则

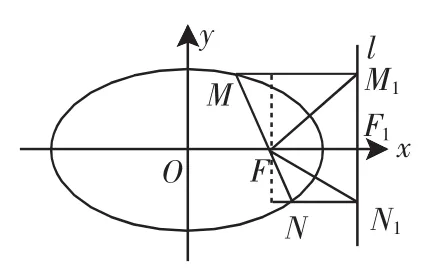
图3

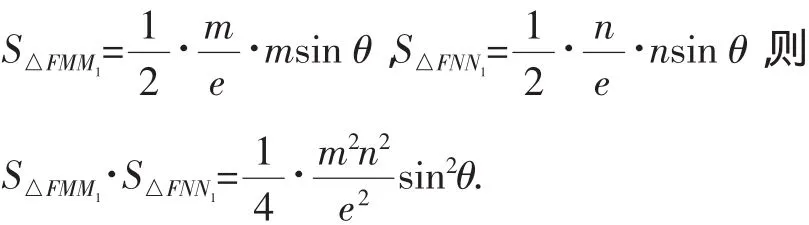
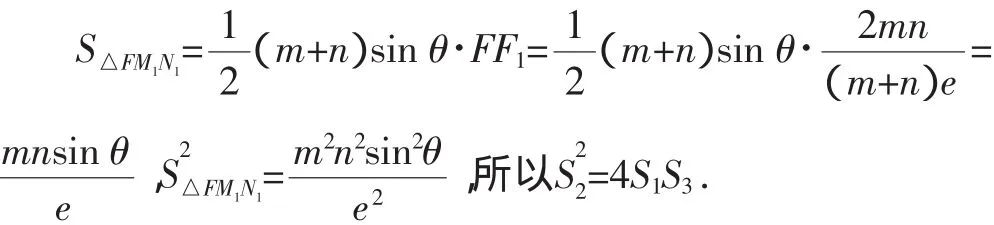
若过F的直线交双曲线的两支于两点，可类似证明：

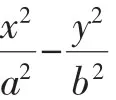
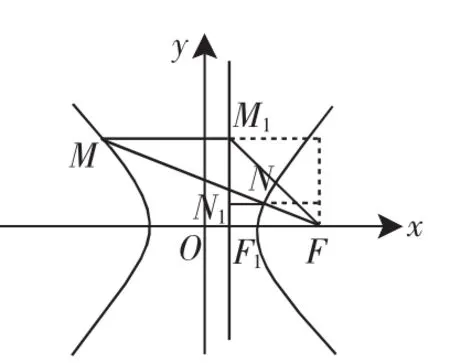
图4

而对于性质2的证明，受其形式联想，可考虑找到一个伸压矩阵变换，若能使点A与直线l在此矩阵作用下，所得的点与直线恰好为变换后椭圆的焦点与准线，那么可直接转化为性质1的证明方法.探索后发现事实确实如此.下面以椭圆为例加以阐述性质2的证明.

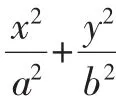
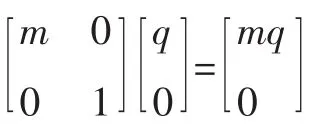
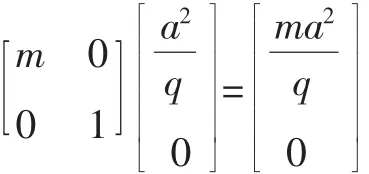
若椭圆①的焦点恰为A′，则m2a2-b2=m2q2，

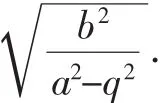
此时椭圆①的准线方程恰为：

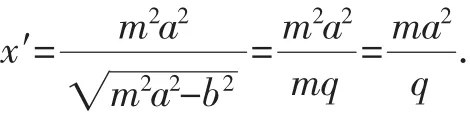
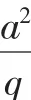
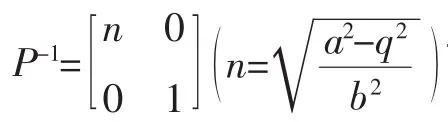
由于在解决圆锥曲线上点到焦点的距离常转化到相应准线的距离，因此过焦点的弦被焦点分成的两条线段长度转化为到相应准线距离时，需要作准线的垂线，恰好与x轴构成三条平行线，如果合理运用线性插值公式，能达到事半功倍的效果.

1.代银．一道高考题的探究［J］．中学数学杂志，2010（11）．

2.徐道．一道高考题引起的联想［J］．数学教学，2010（11）．