圆锥曲线 离开方程 回归几何——一道高考试题的再思考

☉甘肃省兰州市第二十七中学

甘肃省兰州市高中数学谢立亚名师工作室 陈鸿斌

题目 （2012年新课标高考试题（理科）第20题）设抛物线C：x2=2py（p>0）的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点.

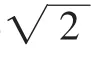
（2）若A，B，F三点在同一条直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到直线m，n距离的比值.

文［1］对此问题进行推广，得到椭圆、双曲线的类似结论：

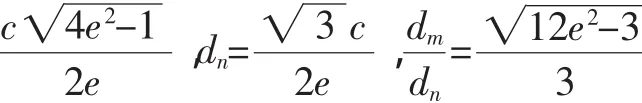
笔者读后颇受感触，对此问题进一步研究，得到了几个新的结论，现介绍如下.

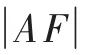
证明：不妨设C为椭圆，如图1所示，连接AD，AB为圆F2的直径，所以AD⊥BD.

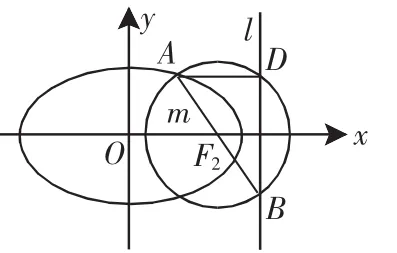
图1

设θ为直线m的倾斜角，则有

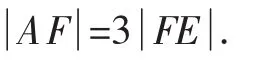
证明：不妨设C为椭圆，如图2所示，证明同上.

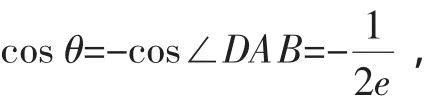
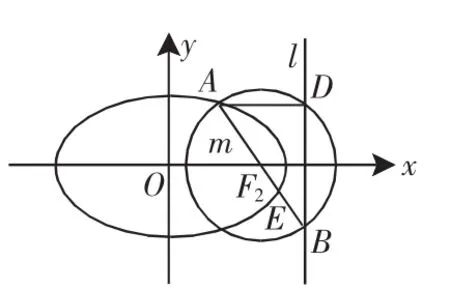
图2

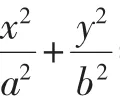
证明：如图3所示，作F1E⊥AB于E，易知△F1F2E∽△BAD.

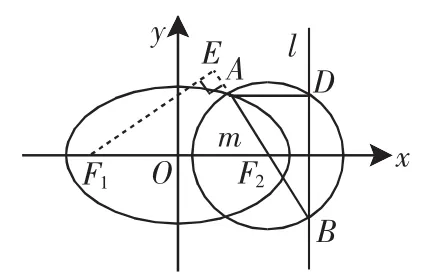
图3

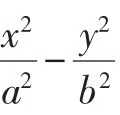
证明：同上，故从略.

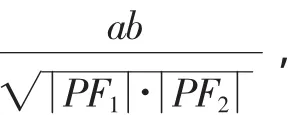
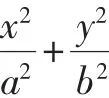
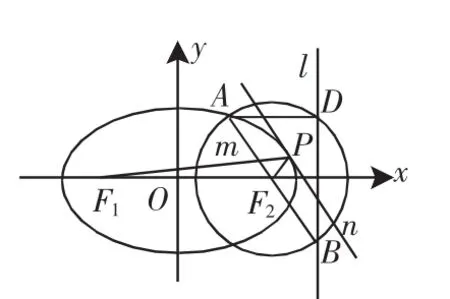
图4

证明：以椭圆为例，如图4所示.

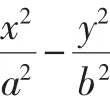
（2）∠F1PF2=120°；

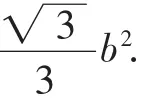
证明同上，故从略.

1.魏泽夫.谈一道高考试题的命题背景及其推广［J］.数学通讯，2013（3）.

2.钱照平.有心二次曲线的心切距［J］.数学通讯，2010（12）.